23.4中位线 同步练习2020-2021学年华东师大版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 23.4中位线 同步练习2020-2021学年华东师大版数学九年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 626.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 10:03:55 | ||
图片预览


文档简介
中位线
一、单选题
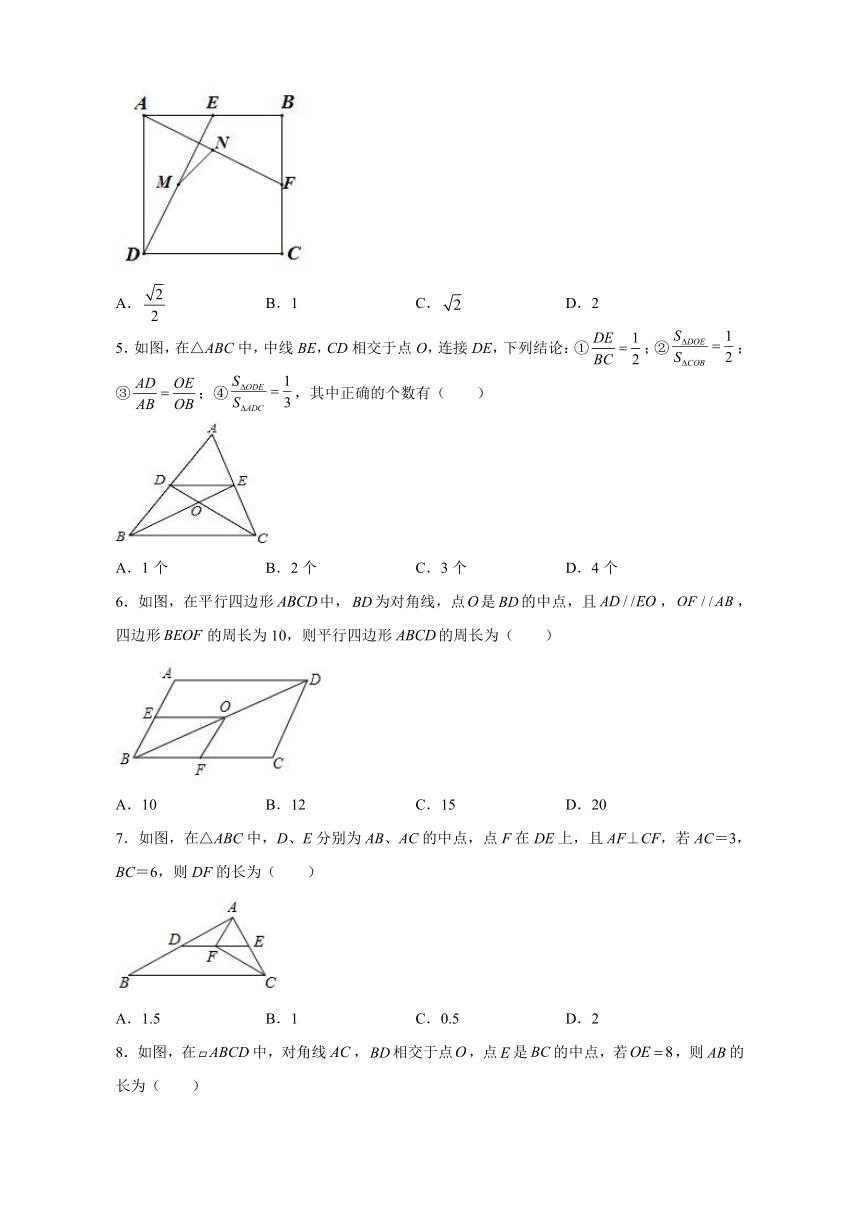
1.如图,在△ABC中,F为BC的中点,点E是AC边上的一点,且AC=10,当AE的长为( )时,EF∥AB
A.3 B.4 C.5 D.4.5
2.如图,已知在中,,,分别是边,,的中点,,,则四边形AFDE的周长等于( )
A.18 B.16 C.14 D.12
3.如图,在 ABCD中,对角线AC、BD相交于点O,在DA的延长线上取点E,连接OE交AB于点F,已知AD=11,CD=14,且AF=2,则AE的长为( )
A.2.3 B.2.2 C.2.1 D.2
4.如图,在正方形中,,,分别为边,的中点,连接,,点,分别为,的中点,连接.则的长为( )
A. B.1 C. D.2
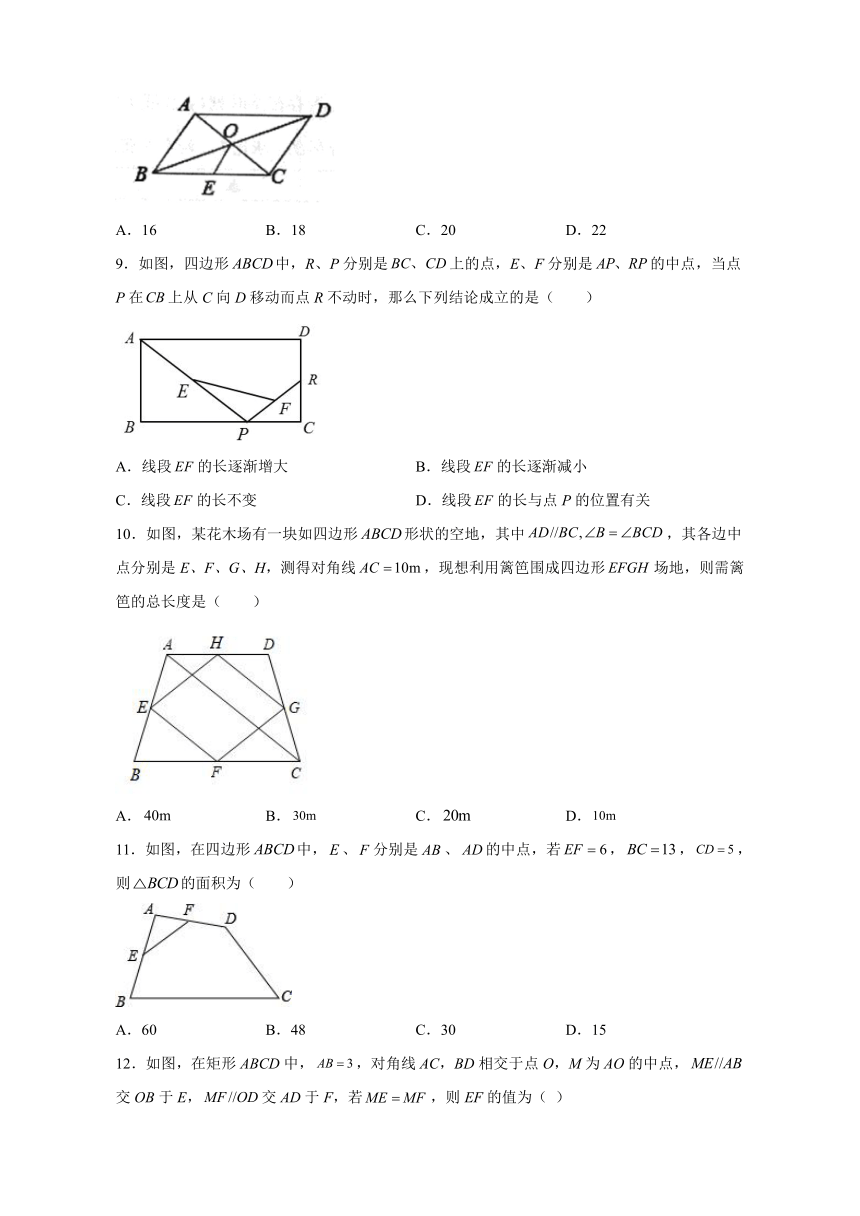
5.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①;②;③;④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平行四边形中,为对角线,点是的中点,且,,四边形的周长为10,则平行四边形的周长为( )
A.10 B.12 C.15 D.20
7.如图,在△ABC中,D、E分别为AB、AC的中点,点F在DE上,且AF⊥CF,若AC=3,BC=6,则DF的长为( )
A.1.5 B.1 C.0.5 D.2
8.如图,在中,对角线,相交于点,点是的中点,若,则的长为( )
A.16 B.18 C.20 D.22
9.如图,四边形中,R、P分别是上的点,E、F分别是的中点,当点P在上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段的长逐渐增大 B.线段的长逐渐减小
C.线段的长不变 D.线段的长与点P的位置有关
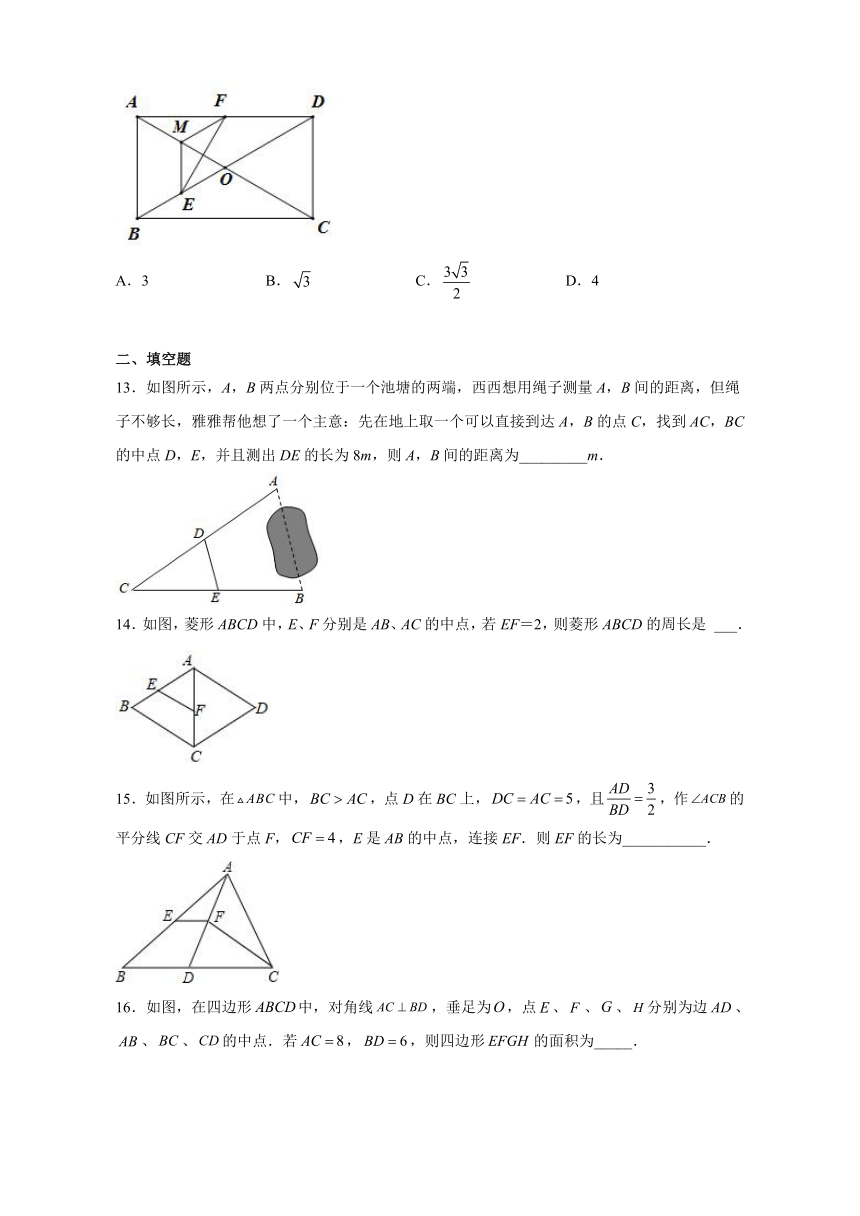
10.如图,某花木场有一块如四边形形状的空地,其中,其各边中点分别是E、F、G、H,测得对角线,现想利用篱笆围成四边形场地,则需篱笆的总长度是( )
A. B. C. D.
11.如图,在四边形中,、分别是、的中点,若,,,则的面积为( )
A.60 B.48 C.30 D.15
12.如图,在矩形ABCD中,,对角线AC,BD相交于点O,M为AO的中点,交OB于E,交AD于F,若,则EF的值为( )
A.3 B. C. D.4
二、填空题
13.如图所示,A,B两点分别位于一个池塘的两端,西西想用绳子测量A,B间的距离,但绳子不够长,雅雅帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为8m,则A,B间的距离为_________m.
14.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=2,则菱形ABCD的周长是 ___.
15.如图所示,在中,,点D在BC上,,且,作的平分线CF交AD于点F,,E是AB的中点,连接EF.则EF的长为___________.
16.如图,在四边形中,对角线,垂足为,点、、、分别为边、、、的中点.若,,则四边形的面积为_____.
17.如图,在中,,,是边的中点,是边上一点,若平分的周长,则的长是______.
三、解答题
18.如图,在中,,,是的中位线,连接,.求证:.
19.如图,正方形中,对角线交于点O,平分交于F.求证:.
20.如图,在中,、分别是、的中点,连接并延长至点,使,连接.
(1)求证:四边形是平行四边形;
(2)探究:当满足什么条件时,四边形是矩形,并说明理由.
21.已知正方形ABCD,点F是射线DC上一动点(不与C、D重合),连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想GFC的形状并说明理由.
(2)取DF中点M,连结MG.若MG=5,正方形边长为8,求BE的长.
22.已知:在△ABC中,AB=AC,AD⊥BC,垂足为点D,E在CB的延长线上,且BE=2BD,连接AE,F是AC的中点,G是AE的中点,连接BG、BF.
(1)如图1,求证:四边形AGBF是平行四边形.
(2)如图2,连接GF、DF,GF与AB相交于点H,若GF=AB,在不添加任何辅助线的情况下,请直接写出图2中所有的等边三角形.
参考答案
1.C
解:当为的中点时,∵F为BC的中点
∴为的中位线,
∴
此时
故选C
2.A
解:∵D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,
∴DE=AB=5,DF=AC=4,AF=AB=5,AE=AC=4,
∴四边形AFDE的周长=AF+DF+DE+AE=5+5+4+4=18,
故选:A.
3.B
解:过O点作OM∥AB,交AD于M,
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD=14,
∴O为BD的中点,
又∵OM∥AB,
∴OM是△ABD的中位线,
∴AM=DM=AD=,OM=AB=7.
∵AF∥OM,
∴△AEF∽△MEO,
∴,
∴,
∴AE=.
故选B.
4.B
解:如图所示,连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴,,,
∴,,
∵M是DE的中点,
∴EM=DM,
在和中,
∴(AAS),
∴,,
∴,
∵点N是为AF的中点,
∴,
∵F是BC的中点,
∴,
在中,根据勾股定理,
,
∴,
故选B.
5.C
解:①∵BE、CD是△ABC的中线,即D、E是AB和AC的中点,
∴DE是△ABC的中位线,
∴ 即,
故①正确;
②∵DE是△ABC的中位线,
∴DE∥BC,
∴△DOE∽△COB,
∴,
故②错误;
③∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵△DOE∽△COB,
,
∴,
故③正确;
④∵△ABC的中线BE与CD交于点O,
∴点O是△ABC的重心,
根据重心性质,BO=2OE,△ABC中上的高=3△BOC中上的高,
且△ABC与△BOC同底(BC),
∴,
由②和③知,,,
∴,
∴,
∴.
故④正确.
综上,①③④正确.
故选C.
6.D
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵点O是BD的中点,且AD//EO,OF//AB,
∴OE,OF分别是三角形ABD,三角形BCD的中位线,BC//EO,
∴四边形OEBF是平行四边形,AD=2OE,CD=2OF,OE=BF,OF=BE,
∵四边形OEBF的周长为10,
∴OE+BE+BF+OF=10,
∴OE+OF=5,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴四边形ABCD的周长=AB+BC+AD+CD=2(AD+CD)=4(OE+OF)=20,
故选D.
7.A
解:、分别为、的中点,,
,
,
,
为的中点,,
,
,
故选:A.
8.A
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,
∵E是BC的中点,
∴OE是△BCD的中位线,
∴CD=2EO,
∵EO=8,
∴CD=2EO=16,
∴AB=CD=16,
故选:A.
9.C
解:如图,连接
四边形中,R、P分别是上的点,当点P在上从C向D移动而点R不动,
的长度是定值,
E、F分别是的中点,
的长度是定值.
故选:
10.C
解:过点A作AM∥DC交BC于点M,连接BD
则∠DCB=∠AMB
∵∠DCB=∠ABC
∴∠AMB=∠ABC
∴AM=AB
∵AD∥BC,AM∥DC
∴四边形AMCD是平行四边形
∴AM=DC
∴AB=DC
在△ABC与△DCB中
∴△ABC≌△DCB(SAS)
∴BD=AC=10m
∵E、F、G、H分别为AB、BC、CD、AD的中点
∴GH=EF=,EH=FG=
∴四边形EFGH是平行四边形
则篱笆的总长度为2(GH+EH)=20(m)
故选:C.
11.C
解:连接BD,
∵E、F分别是AB、AD中点,
∴BD=2EF=12,
∵CD2+BD2=25+144=169,BC2=169,
∴CD2+BD2=BC2,
∴∠BDC=90°,
∴S△DBC=BD CD=×12×5=30,
故选:C.
12.C
解:如图,连接AE,
∵M为AO的中点,ME∥AB,MF∥OD,
∴ME是△ABO的中位线,MF是△AOD的中位线,
∴AB=2ME,OD=2MF,
∵ME=MF,
∴AB=OD,
∵四边形ABCD是矩形,
∴AC=BD,AO=OC,OB=OD,
∴OD=OA=OB,
∴AB=AO=BO=3,
∴△ABO是等边三角形,BD=6,
∴AD=,
∵△ABO是等边三角形,点E是BO中点,
∴AE⊥BO,
又∵点F是AD的中点,
∴EF=AD=,
故选:C.
13.16
解:∵点D,E是AC,BC的中点,DE=8m,
∴AB=2DE=16(m),
故答案为:16.
14.
解:四边形是菱形,
,
E、F分别是AB、AC的中点,EF=2,
,
菱形ABCD的周长为.
故答案为:.
15.
解:∵的平分线CF交AD于点F,,
∴,
∵,
在中,,
∴,
∵,
∴,
∵E是AB的中点,是的中点,
∴是的中位线,
∴.
故答案为:2.
16.12
解:∵点、是边、的中点,
∴,且,
同理可得:,且,
又∵,
∴,,且,
∴四边形是矩形,
∴四边形的面积;
故答案是12.
17.
解:如解图,延长至,使,连接,过点作于,
∵平分的周长,
∴,又,
∴,,
∵,
∴,
∵,
∴,,,
∴,
∴,
∴,
∴,
∴.
18.见解析
解:∵DE、DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形DEAF是平行四边形,
∵∠CAB=90°,
∴四边形DEAF是矩形,
∴EF=AD.
19.见解析
解:∵正方形 ABCD
∴O是BD的中点,
作OG∥AB交BE于点G.
∴OG是△BDE的中位线,
∴OG=DE,
∵正方形ABCD中,∠ABD=∠DBC=45°,
又∵BE是∠DBC的平分线,
∴∠DBE=×45°=22.5°
∴∠ABF=45°+22.5°=67.5°.
∵AB∥OG,
∴∠OGF=∠ABF=67.5°,
又∵在△ABF中,∠BAF=45°,
∴∠AFB=180°-45°-67.5°=67.5°,
∴∠OGF=∠AFB,
∴OF=OG,
∴OF=DE.
20.(1)见解析;(2)当时,四边形是矩形.理由见解析
解:(1)∵、分别是、的中点,
∴,且,
又∵,
∴,
∴四边形是平行四边形.
(2)当时,平行四边形是矩形.
理由:∵,,
∴
∵、分别是,边上的中点,
∴,
∵,
∴四边形是矩形.
21.(1)①见解析;②GFC是等腰三角形,理由见解析;(2)BE的长为14或2.
解:(1)①∵四边形ABCD是正方形,
∴∠ADB=∠CDB=45°,DA=DC,
在DAH和DCH中,
,
∴DAH≌DCH(SAS),
∴∠DAH=∠DCH;
②解:结论:GFC是等腰三角形,
理由:∵DAH≌DCH,
∴∠DAF=∠DCH,
∵CG⊥HC,
∴∠FCG+∠DCH=90°,
∴∠FCG+∠DAF=90°,
∵∠DFA+∠DAF=90°,∠DFA=∠CFG,
∴∠CFG=∠FCG,
∴GF=GC,
∴GFC是等腰三角形.
(2)①如图当点F在线段CD上时,连接DE.
∵∠GFC=∠GCF,∠GEC+∠GFC=90°,∠GCF+∠GCE=90°,
∴∠GCE=∠GEC,
∴EG=GC=FG,
∵FG=GE,FM=MD,
∴DE=2MG=10,
在RtDCE中,CE===6,
∴BE=BC+CE=8+6=14.
②当点F在线段DC的延长线上时,连接DE.
同法可证GM是DEF的中位线,
∴DE=2GM=10,
在RtDCE中,CE===6,
∴BE=BC﹣CE=8﹣6=2.
综上所述,BE的长为14或2.
22.(1)见解析;(2)图2中等边三角形有:△ABC,△AHF,△CDF,△GHB.
解:(1)∵AB=AC,AD⊥BC,
∴BC=2BD,
∵BE=2BD,
∴BC=BE,
∵F是AC的中点,G是AE的中点,
∴BG∥AC,BF∥AE,
∴四边形AGBF是平行四边形.
(2)∵F是AC的中点,G是AE的中点,
∴GF∥BC,
∵BG∥AC,
∴四边形BGFC是平行四边形,
∴GF=BC,
∵GF=AB,AB=AC,
∴AB=AC=BC,
即△ABC是等边三角形,
∵GF∥BC,DF∥AB,BG∥AC,
∴△AHF∽△ABC,△CDF∽△CBA,△GBH∽△FAH,
∴△AHF,△CDF,△GHB是等边三角形,
综上可得:图2中等边三角形有:△ABC,△AHF,△CDF,△GHB.
一、单选题
1.如图,在△ABC中,F为BC的中点,点E是AC边上的一点,且AC=10,当AE的长为( )时,EF∥AB
A.3 B.4 C.5 D.4.5
2.如图,已知在中,,,分别是边,,的中点,,,则四边形AFDE的周长等于( )
A.18 B.16 C.14 D.12
3.如图,在 ABCD中,对角线AC、BD相交于点O,在DA的延长线上取点E,连接OE交AB于点F,已知AD=11,CD=14,且AF=2,则AE的长为( )
A.2.3 B.2.2 C.2.1 D.2
4.如图,在正方形中,,,分别为边,的中点,连接,,点,分别为,的中点,连接.则的长为( )
A. B.1 C. D.2
5.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①;②;③;④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平行四边形中,为对角线,点是的中点,且,,四边形的周长为10,则平行四边形的周长为( )
A.10 B.12 C.15 D.20
7.如图,在△ABC中,D、E分别为AB、AC的中点,点F在DE上,且AF⊥CF,若AC=3,BC=6,则DF的长为( )
A.1.5 B.1 C.0.5 D.2
8.如图,在中,对角线,相交于点,点是的中点,若,则的长为( )
A.16 B.18 C.20 D.22
9.如图,四边形中,R、P分别是上的点,E、F分别是的中点,当点P在上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段的长逐渐增大 B.线段的长逐渐减小
C.线段的长不变 D.线段的长与点P的位置有关
10.如图,某花木场有一块如四边形形状的空地,其中,其各边中点分别是E、F、G、H,测得对角线,现想利用篱笆围成四边形场地,则需篱笆的总长度是( )
A. B. C. D.
11.如图,在四边形中,、分别是、的中点,若,,,则的面积为( )
A.60 B.48 C.30 D.15
12.如图,在矩形ABCD中,,对角线AC,BD相交于点O,M为AO的中点,交OB于E,交AD于F,若,则EF的值为( )
A.3 B. C. D.4
二、填空题
13.如图所示,A,B两点分别位于一个池塘的两端,西西想用绳子测量A,B间的距离,但绳子不够长,雅雅帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为8m,则A,B间的距离为_________m.
14.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=2,则菱形ABCD的周长是 ___.
15.如图所示,在中,,点D在BC上,,且,作的平分线CF交AD于点F,,E是AB的中点,连接EF.则EF的长为___________.
16.如图,在四边形中,对角线,垂足为,点、、、分别为边、、、的中点.若,,则四边形的面积为_____.
17.如图,在中,,,是边的中点,是边上一点,若平分的周长,则的长是______.
三、解答题
18.如图,在中,,,是的中位线,连接,.求证:.
19.如图,正方形中,对角线交于点O,平分交于F.求证:.
20.如图,在中,、分别是、的中点,连接并延长至点,使,连接.
(1)求证:四边形是平行四边形;
(2)探究:当满足什么条件时,四边形是矩形,并说明理由.
21.已知正方形ABCD,点F是射线DC上一动点(不与C、D重合),连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想GFC的形状并说明理由.
(2)取DF中点M,连结MG.若MG=5,正方形边长为8,求BE的长.
22.已知:在△ABC中,AB=AC,AD⊥BC,垂足为点D,E在CB的延长线上,且BE=2BD,连接AE,F是AC的中点,G是AE的中点,连接BG、BF.
(1)如图1,求证:四边形AGBF是平行四边形.
(2)如图2,连接GF、DF,GF与AB相交于点H,若GF=AB,在不添加任何辅助线的情况下,请直接写出图2中所有的等边三角形.
参考答案
1.C
解:当为的中点时,∵F为BC的中点
∴为的中位线,
∴
此时
故选C
2.A
解:∵D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,
∴DE=AB=5,DF=AC=4,AF=AB=5,AE=AC=4,
∴四边形AFDE的周长=AF+DF+DE+AE=5+5+4+4=18,
故选:A.
3.B
解:过O点作OM∥AB,交AD于M,
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD=14,
∴O为BD的中点,
又∵OM∥AB,
∴OM是△ABD的中位线,
∴AM=DM=AD=,OM=AB=7.
∵AF∥OM,
∴△AEF∽△MEO,
∴,
∴,
∴AE=.
故选B.
4.B
解:如图所示,连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴,,,
∴,,
∵M是DE的中点,
∴EM=DM,
在和中,
∴(AAS),
∴,,
∴,
∵点N是为AF的中点,
∴,
∵F是BC的中点,
∴,
在中,根据勾股定理,
,
∴,
故选B.
5.C
解:①∵BE、CD是△ABC的中线,即D、E是AB和AC的中点,
∴DE是△ABC的中位线,
∴ 即,
故①正确;
②∵DE是△ABC的中位线,
∴DE∥BC,
∴△DOE∽△COB,
∴,
故②错误;
③∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵△DOE∽△COB,
,
∴,
故③正确;
④∵△ABC的中线BE与CD交于点O,
∴点O是△ABC的重心,
根据重心性质,BO=2OE,△ABC中上的高=3△BOC中上的高,
且△ABC与△BOC同底(BC),
∴,
由②和③知,,,
∴,
∴,
∴.
故④正确.
综上,①③④正确.
故选C.
6.D
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵点O是BD的中点,且AD//EO,OF//AB,
∴OE,OF分别是三角形ABD,三角形BCD的中位线,BC//EO,
∴四边形OEBF是平行四边形,AD=2OE,CD=2OF,OE=BF,OF=BE,
∵四边形OEBF的周长为10,
∴OE+BE+BF+OF=10,
∴OE+OF=5,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴四边形ABCD的周长=AB+BC+AD+CD=2(AD+CD)=4(OE+OF)=20,
故选D.
7.A
解:、分别为、的中点,,
,
,
,
为的中点,,
,
,
故选:A.
8.A
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,
∵E是BC的中点,
∴OE是△BCD的中位线,
∴CD=2EO,
∵EO=8,
∴CD=2EO=16,
∴AB=CD=16,
故选:A.
9.C
解:如图,连接
四边形中,R、P分别是上的点,当点P在上从C向D移动而点R不动,
的长度是定值,
E、F分别是的中点,
的长度是定值.
故选:
10.C
解:过点A作AM∥DC交BC于点M,连接BD
则∠DCB=∠AMB
∵∠DCB=∠ABC
∴∠AMB=∠ABC
∴AM=AB
∵AD∥BC,AM∥DC
∴四边形AMCD是平行四边形
∴AM=DC
∴AB=DC
在△ABC与△DCB中
∴△ABC≌△DCB(SAS)
∴BD=AC=10m
∵E、F、G、H分别为AB、BC、CD、AD的中点
∴GH=EF=,EH=FG=
∴四边形EFGH是平行四边形
则篱笆的总长度为2(GH+EH)=20(m)
故选:C.
11.C
解:连接BD,
∵E、F分别是AB、AD中点,
∴BD=2EF=12,
∵CD2+BD2=25+144=169,BC2=169,
∴CD2+BD2=BC2,
∴∠BDC=90°,
∴S△DBC=BD CD=×12×5=30,
故选:C.
12.C
解:如图,连接AE,
∵M为AO的中点,ME∥AB,MF∥OD,
∴ME是△ABO的中位线,MF是△AOD的中位线,
∴AB=2ME,OD=2MF,
∵ME=MF,
∴AB=OD,
∵四边形ABCD是矩形,
∴AC=BD,AO=OC,OB=OD,
∴OD=OA=OB,
∴AB=AO=BO=3,
∴△ABO是等边三角形,BD=6,
∴AD=,
∵△ABO是等边三角形,点E是BO中点,
∴AE⊥BO,
又∵点F是AD的中点,
∴EF=AD=,
故选:C.
13.16
解:∵点D,E是AC,BC的中点,DE=8m,
∴AB=2DE=16(m),
故答案为:16.
14.
解:四边形是菱形,
,
E、F分别是AB、AC的中点,EF=2,
,
菱形ABCD的周长为.
故答案为:.
15.
解:∵的平分线CF交AD于点F,,
∴,
∵,
在中,,
∴,
∵,
∴,
∵E是AB的中点,是的中点,
∴是的中位线,
∴.
故答案为:2.
16.12
解:∵点、是边、的中点,
∴,且,
同理可得:,且,
又∵,
∴,,且,
∴四边形是矩形,
∴四边形的面积;
故答案是12.
17.
解:如解图,延长至,使,连接,过点作于,
∵平分的周长,
∴,又,
∴,,
∵,
∴,
∵,
∴,,,
∴,
∴,
∴,
∴,
∴.
18.见解析
解:∵DE、DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形DEAF是平行四边形,
∵∠CAB=90°,
∴四边形DEAF是矩形,
∴EF=AD.
19.见解析
解:∵正方形 ABCD
∴O是BD的中点,
作OG∥AB交BE于点G.
∴OG是△BDE的中位线,
∴OG=DE,
∵正方形ABCD中,∠ABD=∠DBC=45°,
又∵BE是∠DBC的平分线,
∴∠DBE=×45°=22.5°
∴∠ABF=45°+22.5°=67.5°.
∵AB∥OG,
∴∠OGF=∠ABF=67.5°,
又∵在△ABF中,∠BAF=45°,
∴∠AFB=180°-45°-67.5°=67.5°,
∴∠OGF=∠AFB,
∴OF=OG,
∴OF=DE.
20.(1)见解析;(2)当时,四边形是矩形.理由见解析
解:(1)∵、分别是、的中点,
∴,且,
又∵,
∴,
∴四边形是平行四边形.
(2)当时,平行四边形是矩形.
理由:∵,,
∴
∵、分别是,边上的中点,
∴,
∵,
∴四边形是矩形.
21.(1)①见解析;②GFC是等腰三角形,理由见解析;(2)BE的长为14或2.
解:(1)①∵四边形ABCD是正方形,
∴∠ADB=∠CDB=45°,DA=DC,
在DAH和DCH中,
,
∴DAH≌DCH(SAS),
∴∠DAH=∠DCH;
②解:结论:GFC是等腰三角形,
理由:∵DAH≌DCH,
∴∠DAF=∠DCH,
∵CG⊥HC,
∴∠FCG+∠DCH=90°,
∴∠FCG+∠DAF=90°,
∵∠DFA+∠DAF=90°,∠DFA=∠CFG,
∴∠CFG=∠FCG,
∴GF=GC,
∴GFC是等腰三角形.
(2)①如图当点F在线段CD上时,连接DE.
∵∠GFC=∠GCF,∠GEC+∠GFC=90°,∠GCF+∠GCE=90°,
∴∠GCE=∠GEC,
∴EG=GC=FG,
∵FG=GE,FM=MD,
∴DE=2MG=10,
在RtDCE中,CE===6,
∴BE=BC+CE=8+6=14.
②当点F在线段DC的延长线上时,连接DE.
同法可证GM是DEF的中位线,
∴DE=2GM=10,
在RtDCE中,CE===6,
∴BE=BC﹣CE=8﹣6=2.
综上所述,BE的长为14或2.
22.(1)见解析;(2)图2中等边三角形有:△ABC,△AHF,△CDF,△GHB.
解:(1)∵AB=AC,AD⊥BC,
∴BC=2BD,
∵BE=2BD,
∴BC=BE,
∵F是AC的中点,G是AE的中点,
∴BG∥AC,BF∥AE,
∴四边形AGBF是平行四边形.
(2)∵F是AC的中点,G是AE的中点,
∴GF∥BC,
∵BG∥AC,
∴四边形BGFC是平行四边形,
∴GF=BC,
∵GF=AB,AB=AC,
∴AB=AC=BC,
即△ABC是等边三角形,
∵GF∥BC,DF∥AB,BG∥AC,
∴△AHF∽△ABC,△CDF∽△CBA,△GBH∽△FAH,
∴△AHF,△CDF,△GHB是等边三角形,
综上可得:图2中等边三角形有:△ABC,△AHF,△CDF,△GHB.
