23.3.4相似三角形的应用 同步练习2020-2021学年华东师大版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 23.3.4相似三角形的应用 同步练习2020-2021学年华东师大版数学九年级上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 860.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 10:32:47 | ||
图片预览

文档简介
相似三角形的应用
一、单选题
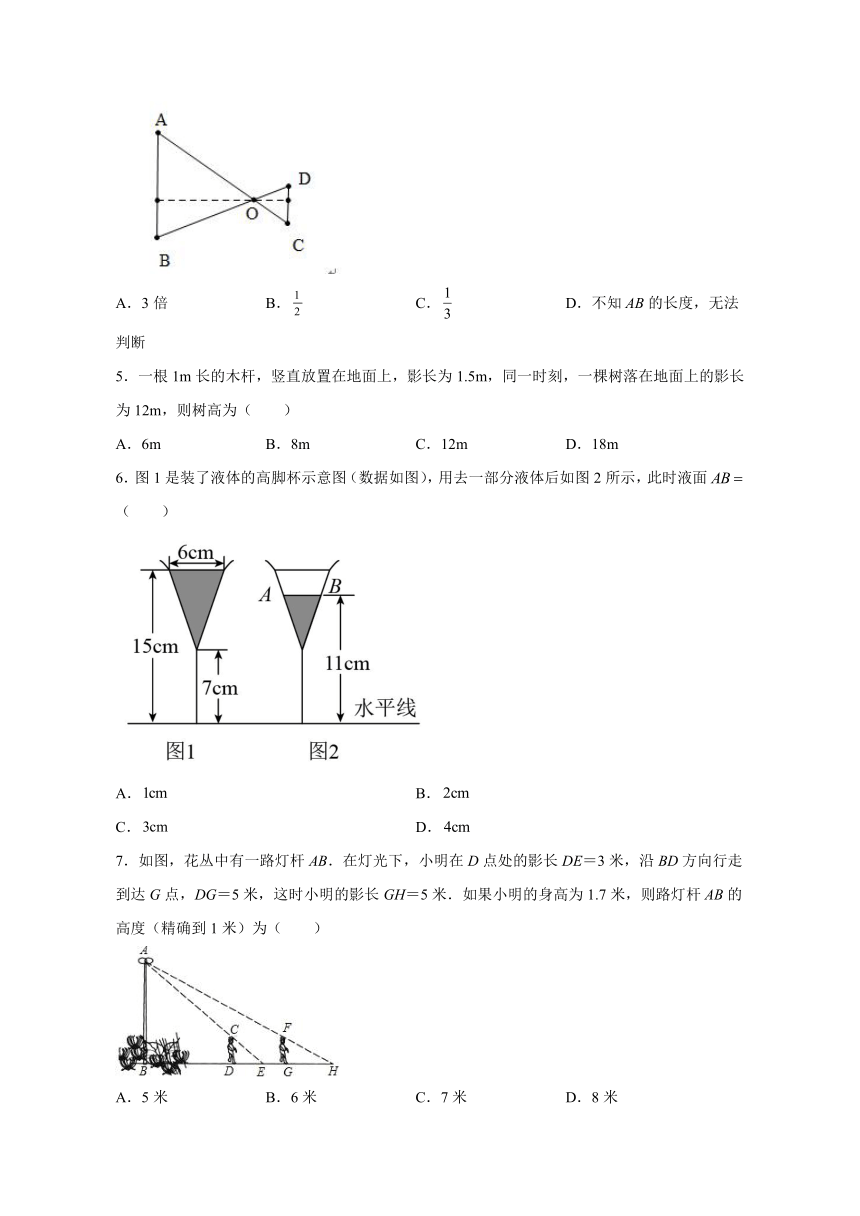
1.如图,一位同学借助镜子测量一棵树的高度,他与树的距离为,当他在镜子中看到树的顶端时,该同学与镜子的距离是远,已知这位同学眼睛到地面的距离是,则树高为( )m.
A.3.4 B.5.1 C.6.8 D.8.5
2.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.2m,测得AB=1.5m,BC=12.5m,则建筑物CD的高是( )
A.10m B.11.2m C.12m D.12.2m
3.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为,当测试距离为时,最大的“”字高度为( )mm
A. B. C. D.
4.在小孔成像问题中, 如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物AB长的( )
A.3倍 B. C. D.不知AB的长度,无法判断
5.一根1m长的木杆,竖直放置在地面上,影长为1.5m,同一时刻,一棵树落在地面上的影长为12m,则树高为( )
A.6m B.8m C.12m D.18m
6.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面( )
A. B.
C. D.
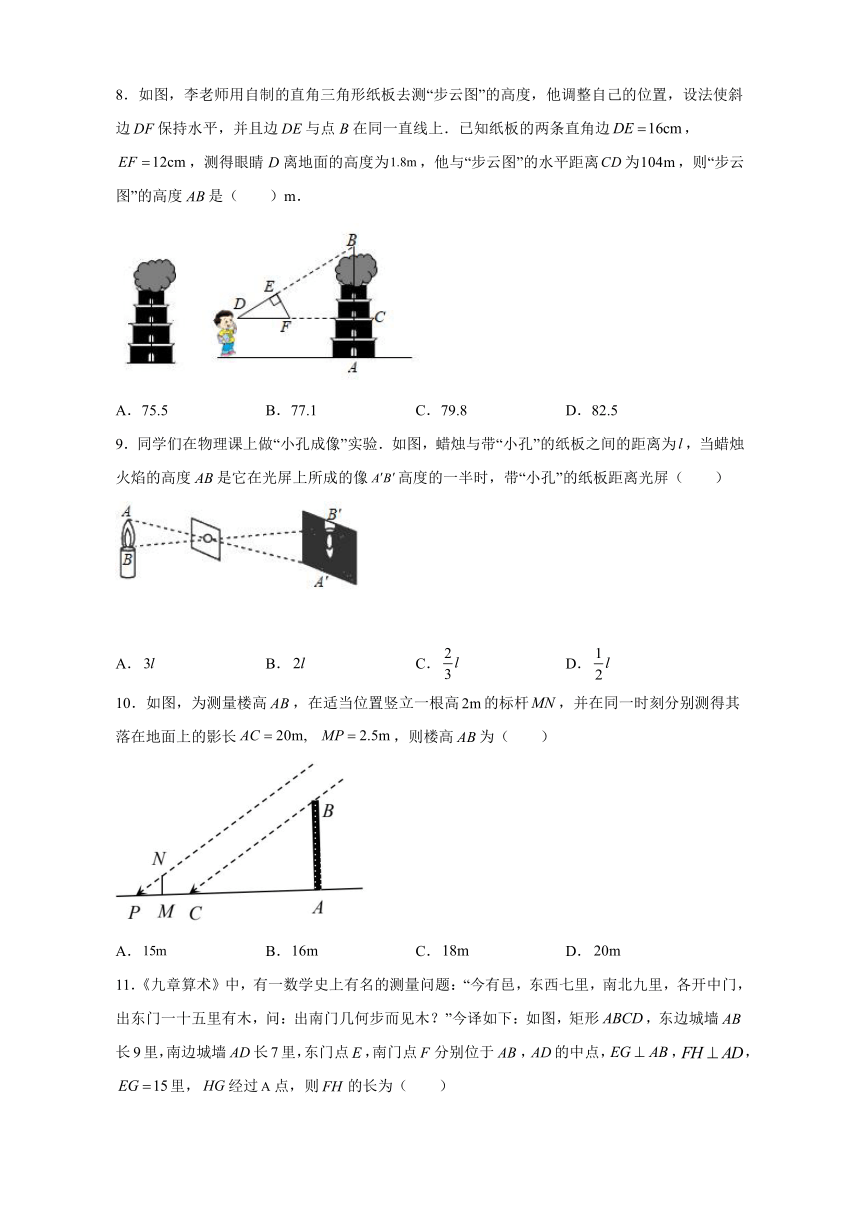
7.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,则路灯杆AB的高度(精确到1米)为( )
A.5米 B.6米 C.7米 D.8米
8.如图,李老师用自制的直角三角形纸板去测“步云图”的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.已知纸板的两条直角边,,测得眼睛D离地面的高度为,他与“步云图”的水平距离为,则“步云图”的高度是( )m.
A.75.5 B.77.1 C.79.8 D.82.5
9.同学们在物理课上做“小孔成像”实验.如图,蜡烛与带“小孔”的纸板之间的距离为,当蜡烛火焰的高度是它在光屏上所成的像高度的一半时,带“小孔”的纸板距离光屏( )
A. B. C. D.
10.如图,为测量楼高,在适当位置竖立一根高的标杆,并在同一时刻分别测得其落在地面上的影长,则楼高为( )
A. B. C. D.
11.《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形,东边城墙长9里,南边城墙长7里,东门点,南门点分别位于,的中点,,,里,经过点,则的长为( )
A.0.95里 B.1.05里 C.2.05里 D.2.15里
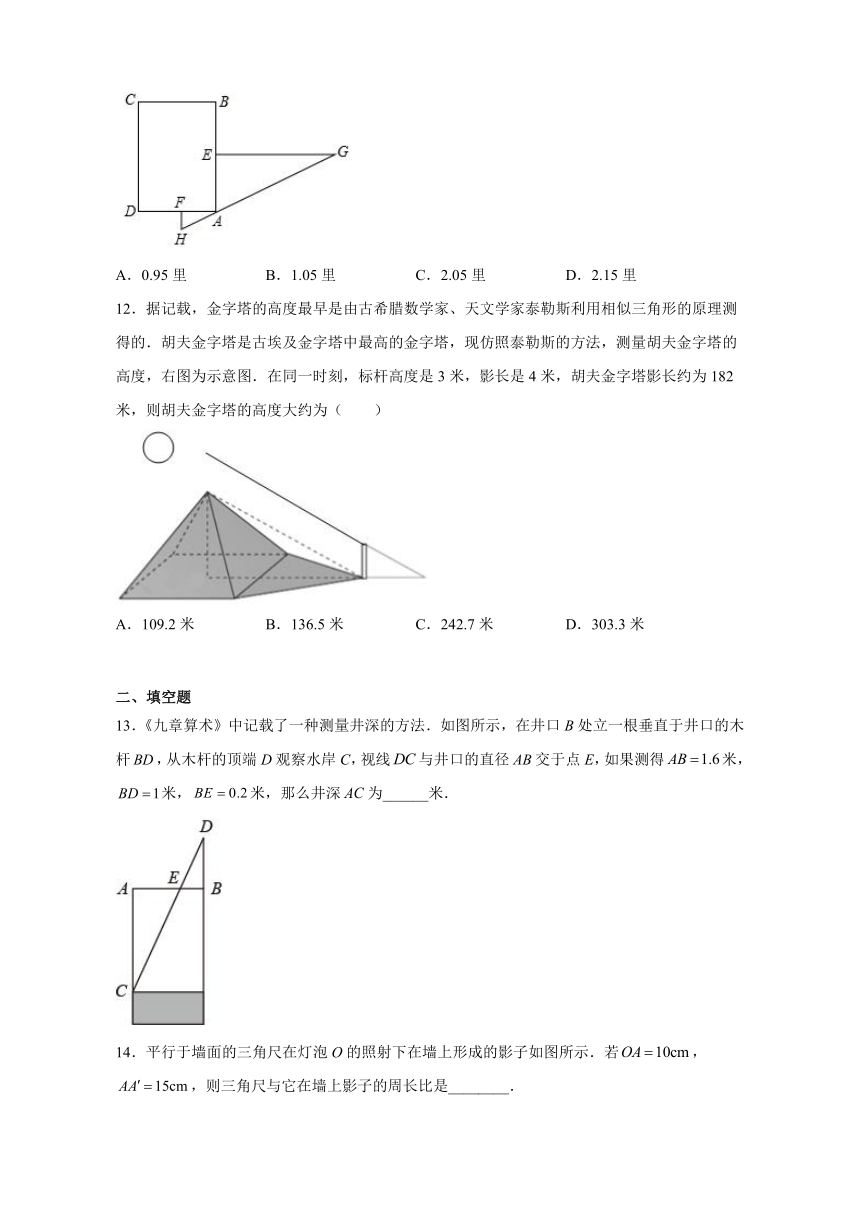
12.据记载,金字塔的高度最早是由古希腊数学家、天文学家泰勒斯利用相似三角形的原理测得的.胡夫金字塔是古埃及金字塔中最高的金字塔,现仿照泰勒斯的方法,测量胡夫金字塔的高度,右图为示意图.在同一时刻,标杆高度是3米,影长是4米,胡夫金字塔影长约为182米,则胡夫金字塔的高度大约为( )
A.109.2米 B.136.5米 C.242.7米 D.303.3米
二、填空题
13.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆,从木杆的顶端D观察水岸C,视线与井口的直径交于点E,如果测得米,米,米,那么井深为______米.
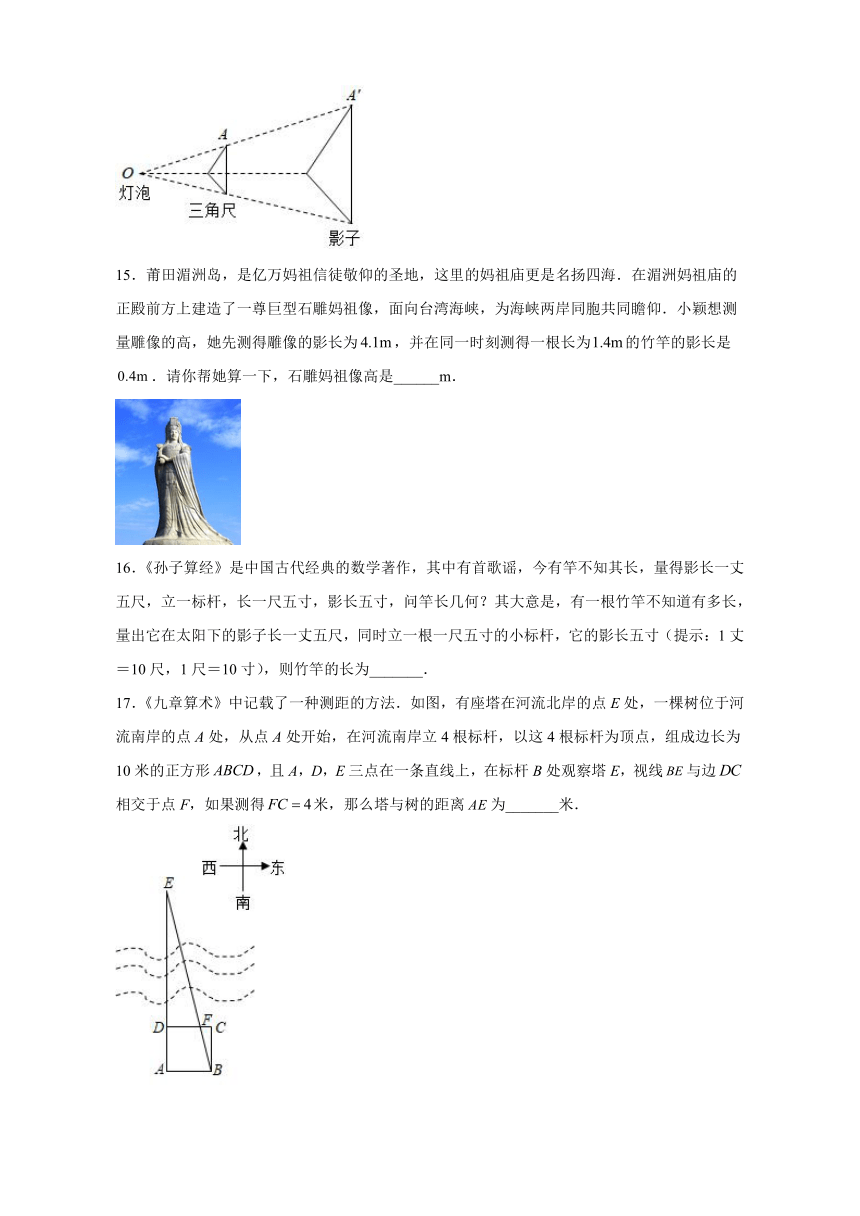
14.平行于墙面的三角尺在灯泡O的照射下在墙上形成的影子如图所示.若,,则三角尺与它在墙上影子的周长比是________.
15.莆田湄洲岛,是亿万妈祖信徒敬仰的圣地,这里的妈祖庙更是名扬四海.在湄洲妈祖庙的正殿前方上建造了一尊巨型石雕妈祖像,面向台湾海峡,为海峡两岸同胞共同瞻仰.小颖想测量雕像的高,她先测得雕像的影长为,并在同一时刻测得一根长为的竹竿的影长是.请你帮她算一下,石雕妈祖像高是______m.
16.《孙子算经》是中国古代经典的数学著作,其中有首歌谣,今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?其大意是,有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为_______.
17.《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线与边相交于点F,如果测得米,那么塔与树的距离为_______米.
三、解答题
18.如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点O,再在他们所在的这一侧选点A,B,D,使得,然后确定和的交点C.测得,你能帮助他们算出峡谷的宽吗?
19.如图,表示一个窗户的高,和表示射入室内的光线,窗户的下端到地面的距离.已知某一时刻在地面的影长,在地面的影长,求窗户的高度.
20.某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的跟晴离地面1.6米,凉亭顶端离地面米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮的身高是1.7米.请根据以上数据求出城楼的高度.
21.如图,两棵树的高度分别为,,两树的根部间的距离,小强正在距树AB的20m的点P处从左向右前进,如果小强的眼睛与地面的距离为1.5m,当小强前进多少米时,就恰好不能看到CD的树顶D
22.如图:AB为路灯主杆,AE为路灯的悬臂,AE长3米,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A、标杆顶端D和地面上一点G在同一直线上,此时路灯E、标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B、标杆底端C和地面上点F、点G在同一水平线上).这时测得FG长1.5米,求路灯主杆AB的高度.
参考答案
1.B
解:如图,由题意得:
而
所以树高为
故选:
2.B
解:依题意,可得,
,
,
,
,
.
故选B.
3.C
解:根据题意,得,且
∴
∴
∴
故选:C.
4.C
解:根据题意得:CD∥AB,
∴△ODC△OBA,
∴.
故选:C.
5.B
解:设树高为xm.
由题意得:,
∴x=8,
∴树高为8m.
故选:B.
6.C
解:由题可知,第一个高脚杯盛液体的高度为:15-7=8(cm),
第二个高脚杯盛液体的高度为:11-7=4(cm),
因为液面都是水平的,图1和图2中的高脚杯是同一个高脚杯,
所以图1和图2中的两个三角形相似,
∴,
∴(cm),
故选:C.
7.B
解:∵DC∥AB,
∴△EDC∽△EBA,
∴=,即=①,
∵FG∥AB,
∴△HGF∽△HBA,
∴=,即=②,
①﹣②得=,解得BD=7.5,
∴=,
∴AB=5.95≈6(米).
即路灯杆AB的高度(精确到1米)为6m.
故选:B.
8.C
解:在和中,,
∴,
∴,
即,
解得:,
∵,
∴,
即“步云图”的高度为.
故选:C.
9.C
解:设纸板与蜡烛的距离是x,
根据题意可得:,
解得:x=,
则纸板与蜡烛的距离是,带“小孔”的纸板距离光屏,
故选:C.
10.B
解:∵,
∴,
∴AB=16(米).
故选:B.
11.B
解:
,
故选:B.
12.B
解:设胡夫金字塔的高度大约为x米,由标杆高度与影长之比等于塔高与影长之比可得:
,
解得.
故选:B.
13.7
解:∵,
∴,
∴,
∵米,米,米,
∴,
解得米,
故井深AC为7米.
14.
解:如图,∵OA=10cm,AA′=15cm,
∴OA′=25cm,
∴,
∵三角尺与影子是相似三角形,
∴三角尺的周长与它在墙上形成的影子的周长的比=,
故答案为:.
15.14.35
解:如图,设石雕妈祖像高为AB,影长为BE,同一时刻竹竿高度为CD,竹竿影长为DE,
∵AB∥CD,
∴△ABE∽△CDE,
∴,
即,
∴AB=14.35m.
故答案为:14.35
16.四丈五尺
解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴,
解得:x=45(尺),
45尺=四丈五尺.
故答案为:四丈五尺.
17.25
解:∵四边形ABCD为正方形,边长为10米,
∴AD=CD=BC=10,FD=CD-CF=6,
∵AD∥BC,且A,D,E三点在一条直线上,
∴AE∥BC,
∴△FDE∽△FCB,
∴,
即:,
∴ED=15,
∴AE=AD+ED=25米,
故答案为:25.
18.
解:∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
解得:,
即峡谷得宽是.
19.
解:,
,
,
即,解得,
,
即窗户的高度为:.
20.
解:过点作于点,交于点,
由题意得:,,,
∵,
∴,
∴,
∴,
解得:,
∵,
故城楼的高度为:,
答:城楼的高度为.
21.小强前进11米时,就恰好不能看到CD的树顶D.
解:由题可知:,,,,
∴,
∵∴
又∵∴.
∴,即
设为,则
∴
∴经检验可知,是原分式方程的根,即.
∴
答:小强前进11米时,就恰好不能看到CD的树顶D.
22.路灯主杆的高度为5.4米.
解:过点作于,交于点,
,,
,
,
,
等于的边上的高,
,,,
,
米.米,
,
,
,即,
(米,
(米,
答:路灯主杆的高度为5.4米.
一、单选题
1.如图,一位同学借助镜子测量一棵树的高度,他与树的距离为,当他在镜子中看到树的顶端时,该同学与镜子的距离是远,已知这位同学眼睛到地面的距离是,则树高为( )m.
A.3.4 B.5.1 C.6.8 D.8.5
2.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.2m,测得AB=1.5m,BC=12.5m,则建筑物CD的高是( )
A.10m B.11.2m C.12m D.12.2m
3.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为,当测试距离为时,最大的“”字高度为( )mm
A. B. C. D.
4.在小孔成像问题中, 如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物AB长的( )
A.3倍 B. C. D.不知AB的长度,无法判断
5.一根1m长的木杆,竖直放置在地面上,影长为1.5m,同一时刻,一棵树落在地面上的影长为12m,则树高为( )
A.6m B.8m C.12m D.18m
6.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面( )
A. B.
C. D.
7.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,则路灯杆AB的高度(精确到1米)为( )
A.5米 B.6米 C.7米 D.8米
8.如图,李老师用自制的直角三角形纸板去测“步云图”的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.已知纸板的两条直角边,,测得眼睛D离地面的高度为,他与“步云图”的水平距离为,则“步云图”的高度是( )m.
A.75.5 B.77.1 C.79.8 D.82.5
9.同学们在物理课上做“小孔成像”实验.如图,蜡烛与带“小孔”的纸板之间的距离为,当蜡烛火焰的高度是它在光屏上所成的像高度的一半时,带“小孔”的纸板距离光屏( )
A. B. C. D.
10.如图,为测量楼高,在适当位置竖立一根高的标杆,并在同一时刻分别测得其落在地面上的影长,则楼高为( )
A. B. C. D.
11.《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形,东边城墙长9里,南边城墙长7里,东门点,南门点分别位于,的中点,,,里,经过点,则的长为( )
A.0.95里 B.1.05里 C.2.05里 D.2.15里
12.据记载,金字塔的高度最早是由古希腊数学家、天文学家泰勒斯利用相似三角形的原理测得的.胡夫金字塔是古埃及金字塔中最高的金字塔,现仿照泰勒斯的方法,测量胡夫金字塔的高度,右图为示意图.在同一时刻,标杆高度是3米,影长是4米,胡夫金字塔影长约为182米,则胡夫金字塔的高度大约为( )
A.109.2米 B.136.5米 C.242.7米 D.303.3米
二、填空题
13.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆,从木杆的顶端D观察水岸C,视线与井口的直径交于点E,如果测得米,米,米,那么井深为______米.
14.平行于墙面的三角尺在灯泡O的照射下在墙上形成的影子如图所示.若,,则三角尺与它在墙上影子的周长比是________.
15.莆田湄洲岛,是亿万妈祖信徒敬仰的圣地,这里的妈祖庙更是名扬四海.在湄洲妈祖庙的正殿前方上建造了一尊巨型石雕妈祖像,面向台湾海峡,为海峡两岸同胞共同瞻仰.小颖想测量雕像的高,她先测得雕像的影长为,并在同一时刻测得一根长为的竹竿的影长是.请你帮她算一下,石雕妈祖像高是______m.
16.《孙子算经》是中国古代经典的数学著作,其中有首歌谣,今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?其大意是,有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为_______.
17.《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线与边相交于点F,如果测得米,那么塔与树的距离为_______米.
三、解答题
18.如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点O,再在他们所在的这一侧选点A,B,D,使得,然后确定和的交点C.测得,你能帮助他们算出峡谷的宽吗?
19.如图,表示一个窗户的高,和表示射入室内的光线,窗户的下端到地面的距离.已知某一时刻在地面的影长,在地面的影长,求窗户的高度.
20.某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的跟晴离地面1.6米,凉亭顶端离地面米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮的身高是1.7米.请根据以上数据求出城楼的高度.
21.如图,两棵树的高度分别为,,两树的根部间的距离,小强正在距树AB的20m的点P处从左向右前进,如果小强的眼睛与地面的距离为1.5m,当小强前进多少米时,就恰好不能看到CD的树顶D
22.如图:AB为路灯主杆,AE为路灯的悬臂,AE长3米,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A、标杆顶端D和地面上一点G在同一直线上,此时路灯E、标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B、标杆底端C和地面上点F、点G在同一水平线上).这时测得FG长1.5米,求路灯主杆AB的高度.
参考答案
1.B
解:如图,由题意得:
而
所以树高为
故选:
2.B
解:依题意,可得,
,
,
,
,
.
故选B.
3.C
解:根据题意,得,且
∴
∴
∴
故选:C.
4.C
解:根据题意得:CD∥AB,
∴△ODC△OBA,
∴.
故选:C.
5.B
解:设树高为xm.
由题意得:,
∴x=8,
∴树高为8m.
故选:B.
6.C
解:由题可知,第一个高脚杯盛液体的高度为:15-7=8(cm),
第二个高脚杯盛液体的高度为:11-7=4(cm),
因为液面都是水平的,图1和图2中的高脚杯是同一个高脚杯,
所以图1和图2中的两个三角形相似,
∴,
∴(cm),
故选:C.
7.B
解:∵DC∥AB,
∴△EDC∽△EBA,
∴=,即=①,
∵FG∥AB,
∴△HGF∽△HBA,
∴=,即=②,
①﹣②得=,解得BD=7.5,
∴=,
∴AB=5.95≈6(米).
即路灯杆AB的高度(精确到1米)为6m.
故选:B.
8.C
解:在和中,,
∴,
∴,
即,
解得:,
∵,
∴,
即“步云图”的高度为.
故选:C.
9.C
解:设纸板与蜡烛的距离是x,
根据题意可得:,
解得:x=,
则纸板与蜡烛的距离是,带“小孔”的纸板距离光屏,
故选:C.
10.B
解:∵,
∴,
∴AB=16(米).
故选:B.
11.B
解:
,
故选:B.
12.B
解:设胡夫金字塔的高度大约为x米,由标杆高度与影长之比等于塔高与影长之比可得:
,
解得.
故选:B.
13.7
解:∵,
∴,
∴,
∵米,米,米,
∴,
解得米,
故井深AC为7米.
14.
解:如图,∵OA=10cm,AA′=15cm,
∴OA′=25cm,
∴,
∵三角尺与影子是相似三角形,
∴三角尺的周长与它在墙上形成的影子的周长的比=,
故答案为:.
15.14.35
解:如图,设石雕妈祖像高为AB,影长为BE,同一时刻竹竿高度为CD,竹竿影长为DE,
∵AB∥CD,
∴△ABE∽△CDE,
∴,
即,
∴AB=14.35m.
故答案为:14.35
16.四丈五尺
解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴,
解得:x=45(尺),
45尺=四丈五尺.
故答案为:四丈五尺.
17.25
解:∵四边形ABCD为正方形,边长为10米,
∴AD=CD=BC=10,FD=CD-CF=6,
∵AD∥BC,且A,D,E三点在一条直线上,
∴AE∥BC,
∴△FDE∽△FCB,
∴,
即:,
∴ED=15,
∴AE=AD+ED=25米,
故答案为:25.
18.
解:∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
解得:,
即峡谷得宽是.
19.
解:,
,
,
即,解得,
,
即窗户的高度为:.
20.
解:过点作于点,交于点,
由题意得:,,,
∵,
∴,
∴,
∴,
解得:,
∵,
故城楼的高度为:,
答:城楼的高度为.
21.小强前进11米时,就恰好不能看到CD的树顶D.
解:由题可知:,,,,
∴,
∵∴
又∵∴.
∴,即
设为,则
∴
∴经检验可知,是原分式方程的根,即.
∴
答:小强前进11米时,就恰好不能看到CD的树顶D.
22.路灯主杆的高度为5.4米.
解:过点作于,交于点,
,,
,
,
,
等于的边上的高,
,,,
,
米.米,
,
,
,即,
(米,
(米,
答:路灯主杆的高度为5.4米.
