23.5位似图形 同步练习 2020-2021学年华东师大版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 23.5位似图形 同步练习 2020-2021学年华东师大版九年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 867.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 10:38:13 | ||
图片预览

文档简介
位似图形
一、单选题
1.下列每组的两个图形不是位似图形的是( )
A. B. C. D.
2.下列说法错误的是( )
A.位似图形一定是相似图形
B.相似图形不一定是位似图形
C.位似图形上任意一对对应点到位似中心的距离之比等于相似比
D.位似图形中每组对应点所在的直线必相互平行
3.如图,△ABC与△DEF位似,点O为位似中心,已知BO:OE=2:1,则△ABC与△DEF的面积比是( )
A.9:1 B.4:1 C.3:1 D.2:1
4.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=( )
A. B. C. D.
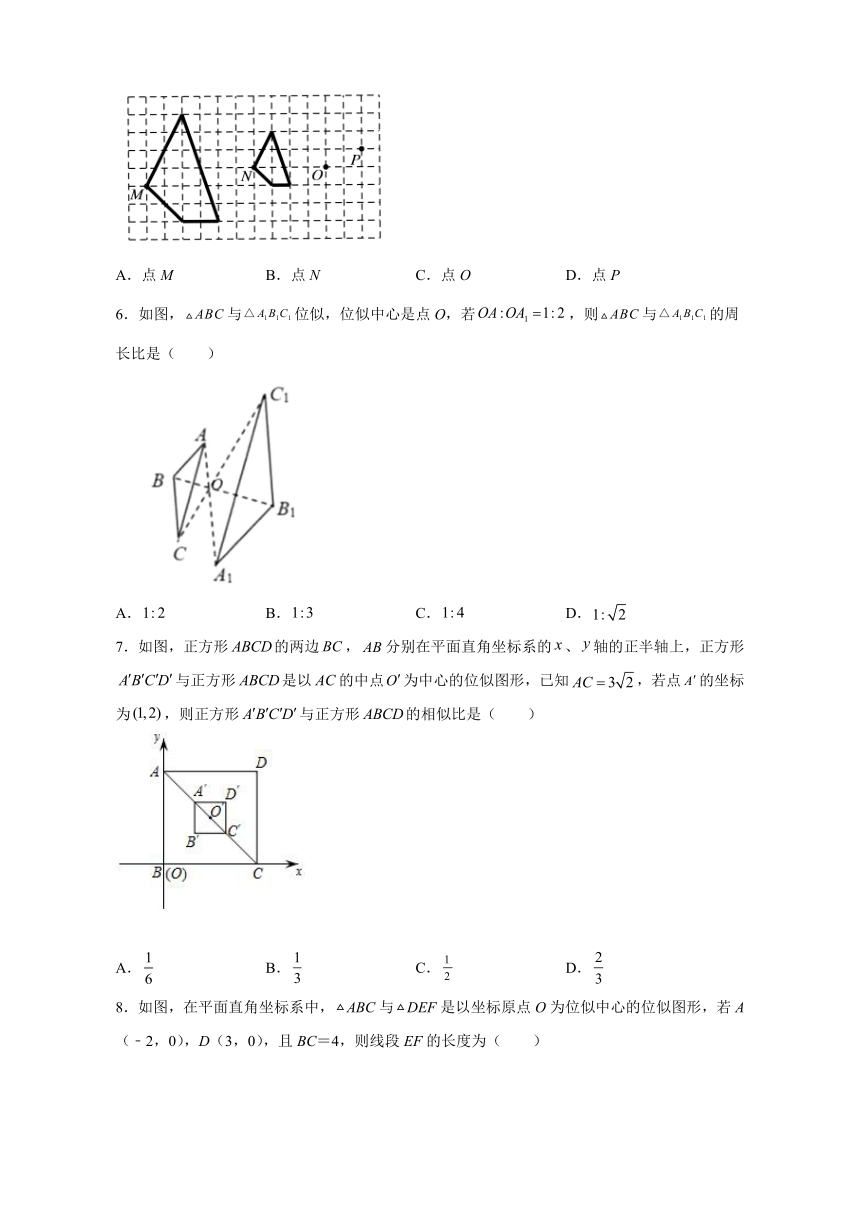
5.如图,两个四边形是位似图形,则它们的位似中心是( )
A.点M B.点N C.点O D.点P
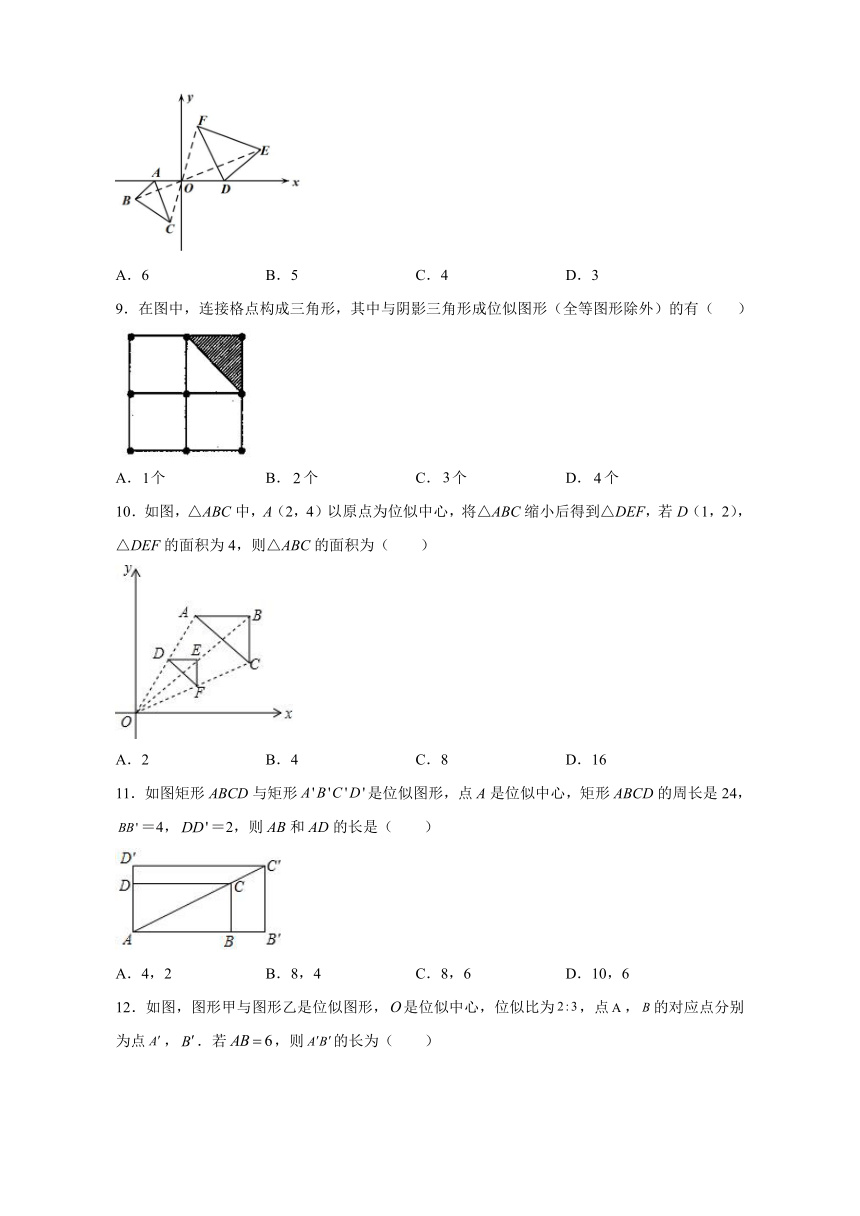
6.如图,与位似,位似中心是点O,若,则与的周长比是( )
A. B. C. D.
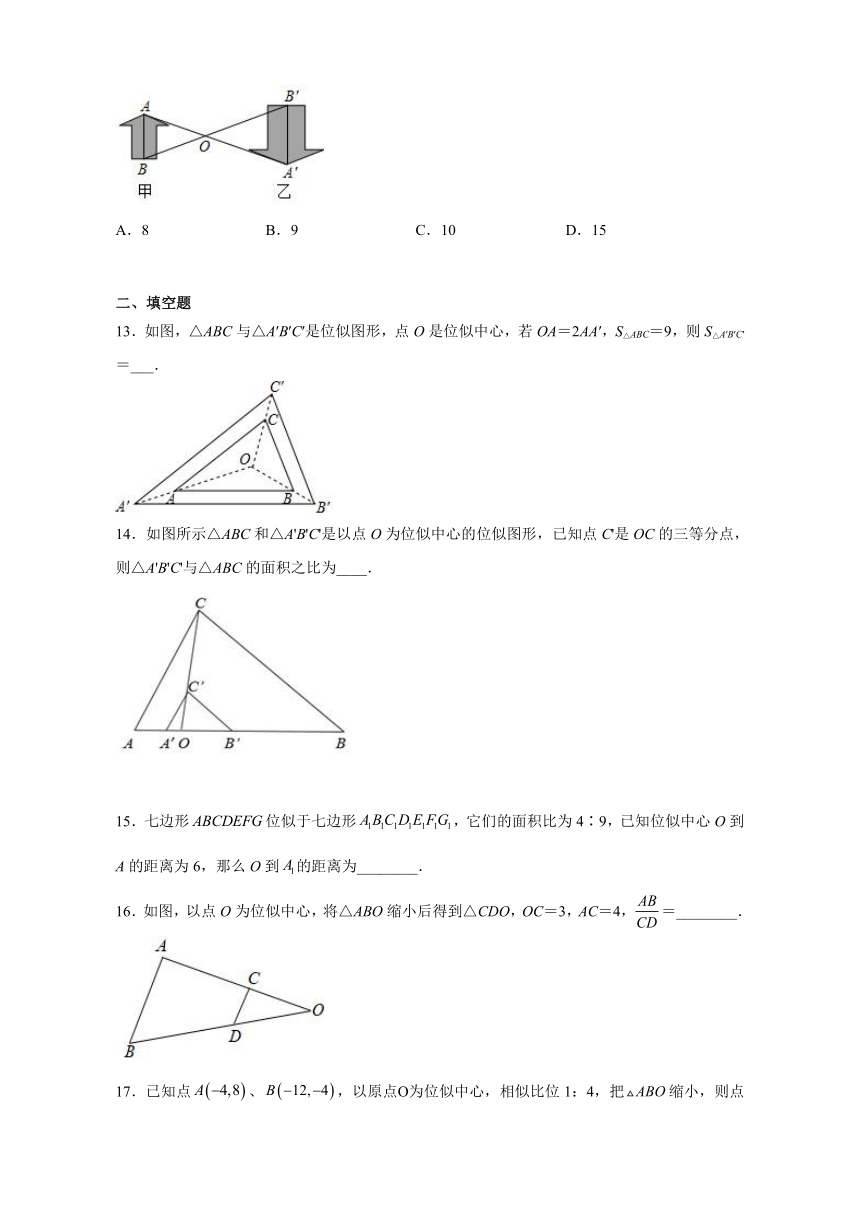
7.如图,正方形的两边,分别在平面直角坐标系的、轴的正半轴上,正方形与正方形是以的中点为中心的位似图形,已知,若点的坐标为,则正方形与正方形的相似比是( )
A. B. C. D.
8.如图,在平面直角坐标系中,ABC与DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且BC=4,则线段EF的长度为( )
A.6 B.5 C.4 D.3
9.在图中,连接格点构成三角形,其中与阴影三角形成位似图形(全等图形除外)的有( )
A.个 B.个 C.个 D.个
10.如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )
A.2 B.4 C.8 D.16
11.如图矩形ABCD与矩形是位似图形,点A是位似中心,矩形ABCD的周长是24,=4,=2,则AB和AD的长是( )
A.4,2 B.8,4 C.8,6 D.10,6
12.如图,图形甲与图形乙是位似图形,是位似中心,位似比为,点,的对应点分别为点,.若,则的长为( )
A.8 B.9 C.10 D.15
二、填空题
13.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=9,则S△A′B′C′=___.
14.如图所示△ABC和△A'B'C'是以点O为位似中心的位似图形,已知点C'是OC的三等分点,则△A'B'C'与△ABC的面积之比为____.
15.七边形位似于七边形,它们的面积比为4∶9,已知位似中心O到A的距离为6,那么O到的距离为________.
16.如图,以点O为位似中心,将△ABO缩小后得到△CDO,OC=3,AC=4,=________.
17.已知点、,以原点О为位似中心,相似比位1:4,把缩小,则点A的对应点的坐标是_______________.
三、解答题
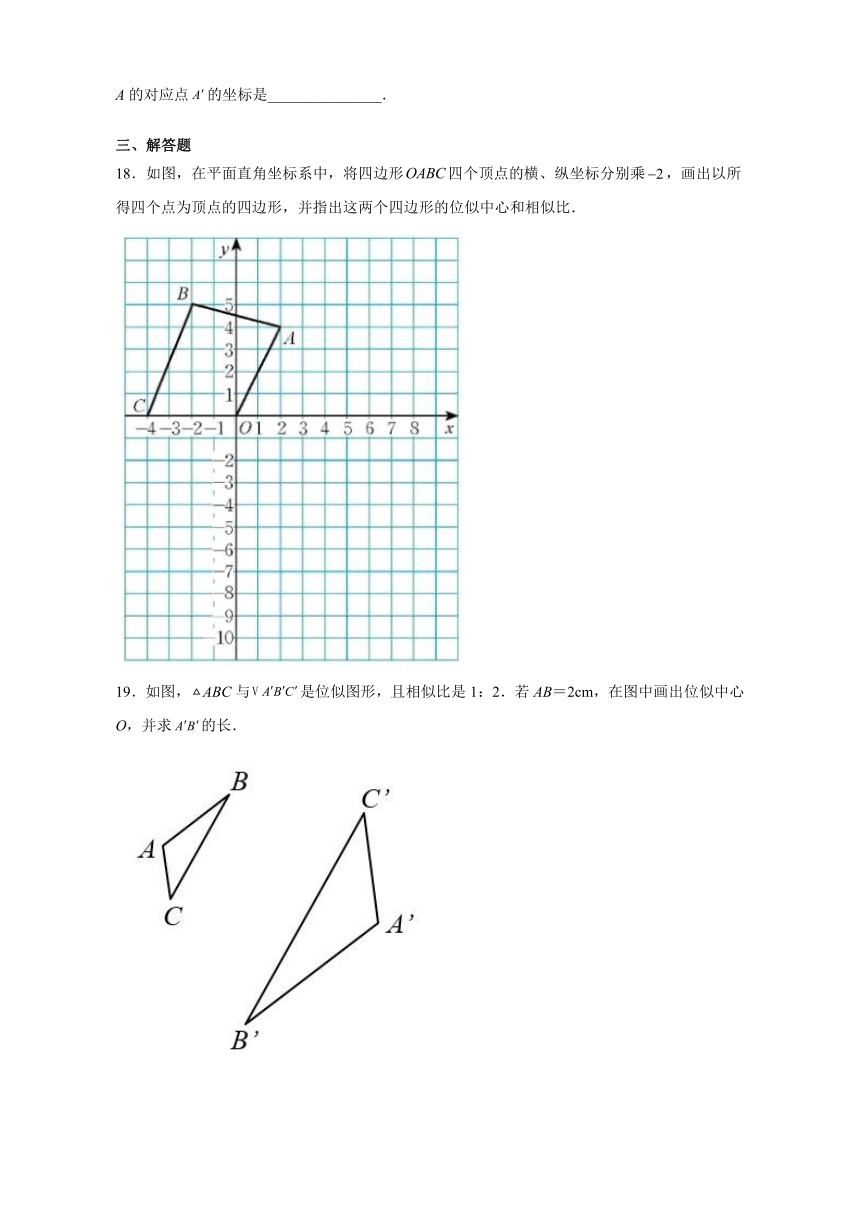
18.如图,在平面直角坐标系中,将四边形四个顶点的横、纵坐标分别乘,画出以所得四个点为顶点的四边形,并指出这两个四边形的位似中心和相似比.
19.如图,ABC与是位似图形,且相似比是1:2.若AB=2cm,在图中画出位似中心O,并求的长.
参考答案
1.D
解:对应顶点的连线相交于一点的两个相似多边形叫位似图形.
据此可得A、B、C三个图形中的两个图形都是位似图形;
而D的对应顶点的连线不能相交于一点,故不是位似图形.
故选:D.
2.D
解:A、位似图形一定是相似图形,所以A选项正确;
B、相似三角形不一定是位似图形,所以B选项正确;
C、位似图形上任意一对对应点到位似中心的距离之比等于相似比,所以C选项正确;
D、位似图形中每组对应点所在的直线相交于一点,不平行,所以D选项错误.
故选:D.
3.B
解:△ABC与△DEF位似,
BO:OE=2:1,
故选B.
4.A
解:∵,
∴,
∵四边形ABCD与四边形EFGH位似,位似中心为点O,
∴EF∥AB,FG∥BC,
∴△OEF∽△OAB,△OGF∽△OCB,
∴,
∴,
故选:A.
5.D
解:如图,位似中心是点P.
故选D
6.A
解:与△位似,
△,,
△,
,
与△的周长比为,
故选:.
7.B
解:延长A′B′交BC于点E,如图.
∵在正方形ABCD中,AC=3,
∴BC=AB=3,
∵点A′的坐标为(1,2),
∴OE=1,EC=A′E=3﹣1=2,
∴CE:BC=2:3,
∵A′E∥AB,
∴△A′CE∽△ACB,
∴CA′:AC=2:3,
∵正方形与正方形是以的中点为中心的位似图形,
∴AA′=CC′,
∴AA′=CC′=A′C′,
∴A′C′:AC=1:3,
∴正方形A′B′C′D′与正方形ABCD的相似比是.
故选:B.
8.A
解:与是以坐标原点为位似中心的位似图形,
,
,,
,,
与的相似比为,
∴BC∶EF=2∶3,
,
,
故选:A.
9.B
解:如图:与构成位似图形.
故选
10.D
解:∵A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,D(1,2),
∴位似比为:2:1,
∴面积比为:4:1,
∵△DEF的面积为4,
∴△ABC的面积为:4×4=16.
故选:D.
11.B
解:∵矩形ABCD的周长是24,
∴AB+AD=12,
∴AD=12﹣AB,
∴AB′=AB+4,AD′=12﹣AB+2=14﹣AB,
∵矩形ABCD与矩形A'B'C'D'是位似图形,
∴CD//C′D′,BC//B′C′,
∴=,=,
∴=,即=,
解得,AB=8,
则AD=12﹣AB=4,
故选:B.
12.B
解:∵图形甲与图形乙是位似图形,是位似中心,位似比为,
∴,
∵,
∴,
∴
故答案为:B.
13.
解:△ABC与△A′B′C′是位似图形且由OA=2AA′.
可得两位似图形的位似比为2:3,所以两位似图形的面积比为4:9,
又S△ABC=9,
∴S△A'B'C′=.
故答案为:.
14.
解:∵点是OC的三等分点
∴
由题意可得,
∴
∴
由相似三角形的性质可得
故答案为
15.9
解:∵位似多边形的面积比为4∶9
∴位似多边形相似比为2∶3
设O到的距离为x
∴6∶x=2∶3,解得x=9
故答案为:9.
16..
解:∵OC=3,AC=4,
∴
∵以点O为位似中心,将△ABO缩小后得到△CDO,
∴
∴
∴=.
故答案为:.
17.(﹣1,2)或(1,﹣2).
解:∵点A(﹣4,8)、B(﹣12,﹣4),以原点O为位似中心,相似比为1:4,把△ABO缩小,
∴A点坐标都乘以或﹣即可得出答案,
则点A的对应点的坐标为:(﹣1,2)或(1,﹣2),
故答案为:(﹣1,2)或(1,﹣2).
18.位似中心是原点,相似比是2∶1.
解:由图可知,点坐标是:,点坐标是: ,点坐标是:, 点坐标是: ,
将四个顶点的横、纵坐标分别乘,可得:点坐标是:, 点坐标是:,点坐标是: ,点坐标是:,
所得四边形如下图所示:
连接,,,可知连线经过原点,
∴所画四边形与四边形的位似中心是原点,相似比是2∶1.
19.画图见解析,cm
解:如图,连接,交点即为位似中心,
相似比是1:2,
,
cm,
cm.
一、单选题
1.下列每组的两个图形不是位似图形的是( )
A. B. C. D.
2.下列说法错误的是( )
A.位似图形一定是相似图形
B.相似图形不一定是位似图形
C.位似图形上任意一对对应点到位似中心的距离之比等于相似比
D.位似图形中每组对应点所在的直线必相互平行
3.如图,△ABC与△DEF位似,点O为位似中心,已知BO:OE=2:1,则△ABC与△DEF的面积比是( )
A.9:1 B.4:1 C.3:1 D.2:1
4.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=( )
A. B. C. D.
5.如图,两个四边形是位似图形,则它们的位似中心是( )
A.点M B.点N C.点O D.点P
6.如图,与位似,位似中心是点O,若,则与的周长比是( )
A. B. C. D.
7.如图,正方形的两边,分别在平面直角坐标系的、轴的正半轴上,正方形与正方形是以的中点为中心的位似图形,已知,若点的坐标为,则正方形与正方形的相似比是( )
A. B. C. D.
8.如图,在平面直角坐标系中,ABC与DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且BC=4,则线段EF的长度为( )
A.6 B.5 C.4 D.3
9.在图中,连接格点构成三角形,其中与阴影三角形成位似图形(全等图形除外)的有( )
A.个 B.个 C.个 D.个
10.如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )
A.2 B.4 C.8 D.16
11.如图矩形ABCD与矩形是位似图形,点A是位似中心,矩形ABCD的周长是24,=4,=2,则AB和AD的长是( )
A.4,2 B.8,4 C.8,6 D.10,6
12.如图,图形甲与图形乙是位似图形,是位似中心,位似比为,点,的对应点分别为点,.若,则的长为( )
A.8 B.9 C.10 D.15
二、填空题
13.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=9,则S△A′B′C′=___.
14.如图所示△ABC和△A'B'C'是以点O为位似中心的位似图形,已知点C'是OC的三等分点,则△A'B'C'与△ABC的面积之比为____.
15.七边形位似于七边形,它们的面积比为4∶9,已知位似中心O到A的距离为6,那么O到的距离为________.
16.如图,以点O为位似中心,将△ABO缩小后得到△CDO,OC=3,AC=4,=________.
17.已知点、,以原点О为位似中心,相似比位1:4,把缩小,则点A的对应点的坐标是_______________.
三、解答题
18.如图,在平面直角坐标系中,将四边形四个顶点的横、纵坐标分别乘,画出以所得四个点为顶点的四边形,并指出这两个四边形的位似中心和相似比.
19.如图,ABC与是位似图形,且相似比是1:2.若AB=2cm,在图中画出位似中心O,并求的长.
参考答案
1.D
解:对应顶点的连线相交于一点的两个相似多边形叫位似图形.
据此可得A、B、C三个图形中的两个图形都是位似图形;
而D的对应顶点的连线不能相交于一点,故不是位似图形.
故选:D.
2.D
解:A、位似图形一定是相似图形,所以A选项正确;
B、相似三角形不一定是位似图形,所以B选项正确;
C、位似图形上任意一对对应点到位似中心的距离之比等于相似比,所以C选项正确;
D、位似图形中每组对应点所在的直线相交于一点,不平行,所以D选项错误.
故选:D.
3.B
解:△ABC与△DEF位似,
BO:OE=2:1,
故选B.
4.A
解:∵,
∴,
∵四边形ABCD与四边形EFGH位似,位似中心为点O,
∴EF∥AB,FG∥BC,
∴△OEF∽△OAB,△OGF∽△OCB,
∴,
∴,
故选:A.
5.D
解:如图,位似中心是点P.
故选D
6.A
解:与△位似,
△,,
△,
,
与△的周长比为,
故选:.
7.B
解:延长A′B′交BC于点E,如图.
∵在正方形ABCD中,AC=3,
∴BC=AB=3,
∵点A′的坐标为(1,2),
∴OE=1,EC=A′E=3﹣1=2,
∴CE:BC=2:3,
∵A′E∥AB,
∴△A′CE∽△ACB,
∴CA′:AC=2:3,
∵正方形与正方形是以的中点为中心的位似图形,
∴AA′=CC′,
∴AA′=CC′=A′C′,
∴A′C′:AC=1:3,
∴正方形A′B′C′D′与正方形ABCD的相似比是.
故选:B.
8.A
解:与是以坐标原点为位似中心的位似图形,
,
,,
,,
与的相似比为,
∴BC∶EF=2∶3,
,
,
故选:A.
9.B
解:如图:与构成位似图形.
故选
10.D
解:∵A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,D(1,2),
∴位似比为:2:1,
∴面积比为:4:1,
∵△DEF的面积为4,
∴△ABC的面积为:4×4=16.
故选:D.
11.B
解:∵矩形ABCD的周长是24,
∴AB+AD=12,
∴AD=12﹣AB,
∴AB′=AB+4,AD′=12﹣AB+2=14﹣AB,
∵矩形ABCD与矩形A'B'C'D'是位似图形,
∴CD//C′D′,BC//B′C′,
∴=,=,
∴=,即=,
解得,AB=8,
则AD=12﹣AB=4,
故选:B.
12.B
解:∵图形甲与图形乙是位似图形,是位似中心,位似比为,
∴,
∵,
∴,
∴
故答案为:B.
13.
解:△ABC与△A′B′C′是位似图形且由OA=2AA′.
可得两位似图形的位似比为2:3,所以两位似图形的面积比为4:9,
又S△ABC=9,
∴S△A'B'C′=.
故答案为:.
14.
解:∵点是OC的三等分点
∴
由题意可得,
∴
∴
由相似三角形的性质可得
故答案为
15.9
解:∵位似多边形的面积比为4∶9
∴位似多边形相似比为2∶3
设O到的距离为x
∴6∶x=2∶3,解得x=9
故答案为:9.
16..
解:∵OC=3,AC=4,
∴
∵以点O为位似中心,将△ABO缩小后得到△CDO,
∴
∴
∴=.
故答案为:.
17.(﹣1,2)或(1,﹣2).
解:∵点A(﹣4,8)、B(﹣12,﹣4),以原点O为位似中心,相似比为1:4,把△ABO缩小,
∴A点坐标都乘以或﹣即可得出答案,
则点A的对应点的坐标为:(﹣1,2)或(1,﹣2),
故答案为:(﹣1,2)或(1,﹣2).
18.位似中心是原点,相似比是2∶1.
解:由图可知,点坐标是:,点坐标是: ,点坐标是:, 点坐标是: ,
将四个顶点的横、纵坐标分别乘,可得:点坐标是:, 点坐标是:,点坐标是: ,点坐标是:,
所得四边形如下图所示:
连接,,,可知连线经过原点,
∴所画四边形与四边形的位似中心是原点,相似比是2∶1.
19.画图见解析,cm
解:如图,连接,交点即为位似中心,
相似比是1:2,
,
cm,
cm.
