2021—2022学年鲁教版(五四制)九年级上册1.2 反比例函数的图像和性质课件(共39张PPT)
文档属性
| 名称 | 2021—2022学年鲁教版(五四制)九年级上册1.2 反比例函数的图像和性质课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 11:23:51 | ||
图片预览







文档简介
(共39张PPT)
反比例函数的图象与性质
“心动”不如行动
列表(在自变量取值勤范围内取一些值,并计算相应的函数值)
连线
做一做
驶向胜利的彼岸
描点
x -8 -4 -2 -1 1 2 4 8
-1
-2
-4
-8
8
4
2
1
x
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
.
y
x
-1
-2
-4
-8
8
4
2
1
x … -8 -4 -2 -1 … 1 2 4 8
… …
.
.
.
.
…
…
.
.
y = —
-4
x
驶向胜利的彼岸
“心动”不如行动
你认为作比例函数图象时应注意哪些问题?
列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;
列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线(平滑的曲线),又较准确地表达函数的变化趋势;
描点时一定要养成按自变量从小到大的顺序 依次画线,从中体会函数的增减性;
……
做一做
5
驶向胜利的彼岸
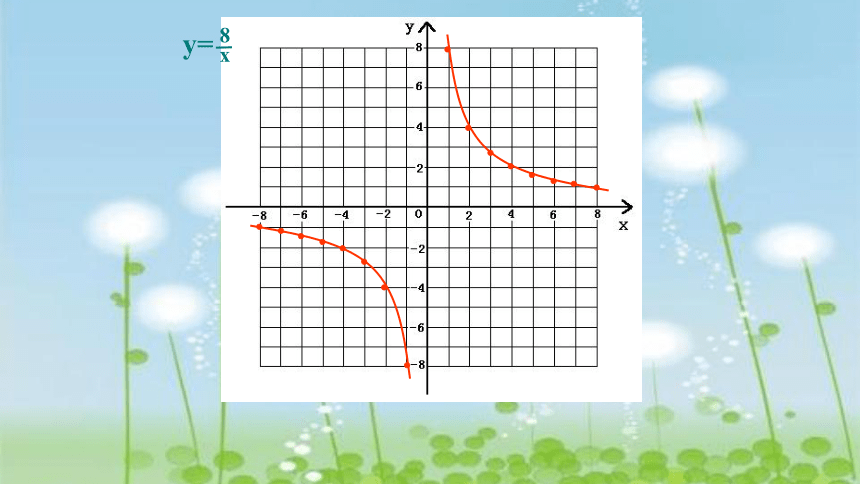
独立完成函数图像
y=
y=-
8
x
8
x
8
x
y=
8
x
y=
y
x
-6
-5
5
1
2
3
4
-8
-7
-4
-3
-2
-1
6
7
8
…
…
1
8/3
…
…
8/7
4/3
8/5
2
4
8
-8
-4
-8/3
-2
-8/5
-4/3
-8/7
-1
反比例函数的图象和性质
“行家”看门道
形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;
想一想
6
驶向胜利的彼岸
反比例函数的图象和性质
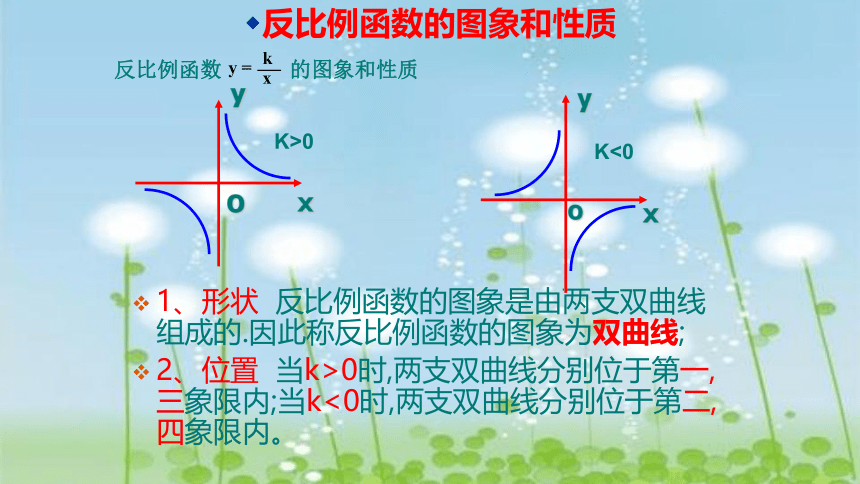
1、形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
2、位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内。
反比例函数 的图象和性质
y =
x
k
y
x
o
x
y
o
K>0
K<0
反比例函数的图象和性质
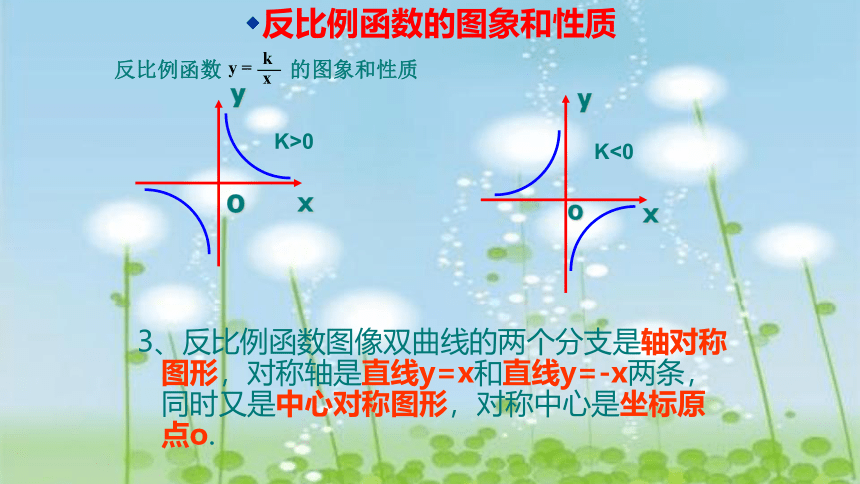
3、反比例函数图像双曲线的两个分支是轴对称图形,对称轴是直线y=x和直线y=-x两条,同时又是中心对称图形,对称中心是坐标原点o.
反比例函数 的图象和性质
y =
x
k
y
x
o
x
y
o
K>0
K<0
“双胞胎”之间的差异
y
x
o
x
y
o
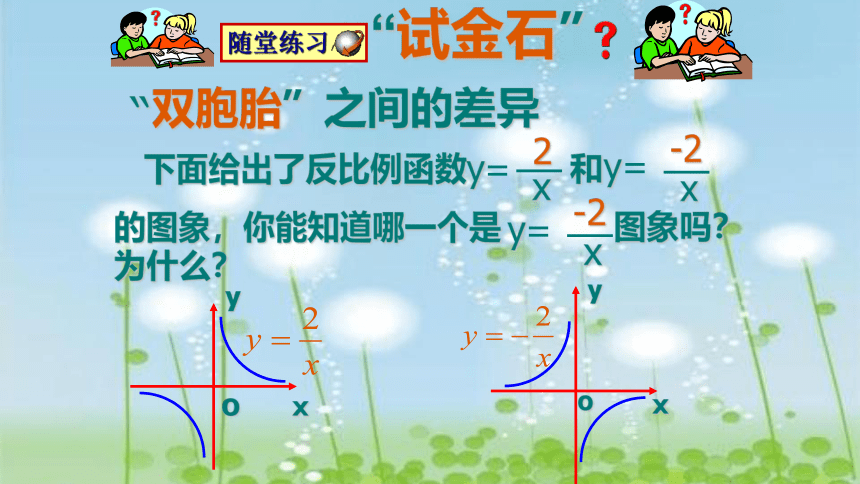
下面给出了反比例函数 和
的图象,你能知道哪一个是 图象吗?为什么?
y=
-2
x
y=
2
x
y=
-2
x
“试金石”
随堂练习
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
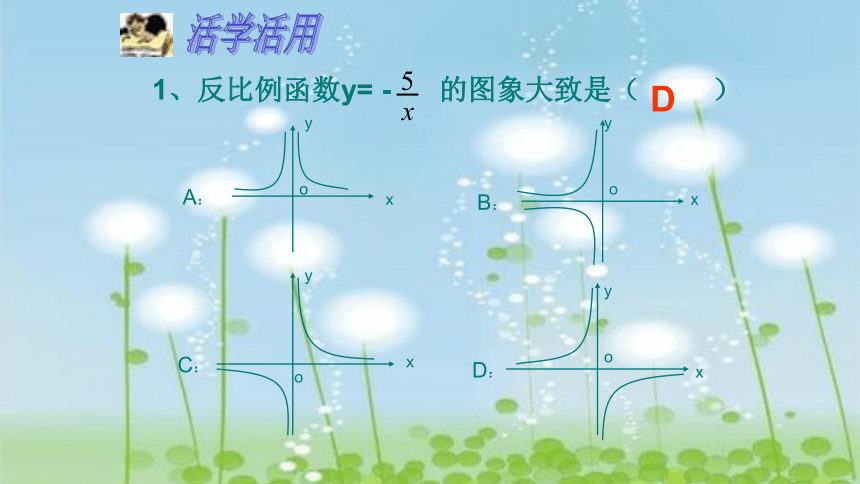
1、反比例函数y= - 的图象大致是( )
D
活学活用
1.函数 的图像在第_____象限,函数 的图象在第 象限。
2. 双曲线 经过点(-3,___)
y =
x
5
y =
1
3x
3.函数 的图像在二、四象限,则m的取值范围是 ____ .
4.对于函数 ,这部分图像在第 ________象限.
y =
1
2x
m-2
x
y =
测一测
二,四
m < 2
一、三
9
1
一、三
例1:如图是反比例函数 的图像的一支
x
o
y
y=
m-6
x
⑴图像的另一只位于哪个象限?常数m的取值范围是什么?
⑵图像经过点(-2,6),判断
点A(-3,4),B(8,- )
C(4,-4)在图像上吗?
3
2
巩固练习;已知反比例函数y= (k≠0)的图象的一支如图。
(1)判断k是正数还是负数;
(2)求这个反比例函数的解析式;
(3)补画这个反比例函数图象的另一支。
y
x
y
0
(-4,2)
基础训练:
1.若y=(a-1)x a是反比例函数,则图象在 象限;
2. 已知变量y与x成反比例,当x=3时,y=-6;那么
当y=3时,x的值是 ;
3.已知点A(-2,a)在函数 的图像上,则 a= ;
4、若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________
k>-1
5、甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)的函数,则这个函数的图象大致是( )
C
在实际问题中图象就可能只有一支。
课内练习:
1、已知反比例函数 (k≠0) 的图象上一点的坐标为( ,2 )。
求这个反比例函数的解析式。
y =
x
k
2、已知y 与 x 成反比例, 并且当 x = 2 时, y = 5,求 x 与 y 的函数关系式。
3、根据图形写出函数的解析式。
y
x
y
0
(-3,1)
y =
x
3
x
10
y =
反比例函数性质
第二课时
y
x
o
x
y
o
观察图像解决一下问题:
1、判断双曲线的k的正负
2、在每个象限内,随着x的逐渐增大,y的变化有什么规律?要注意什么?有哪些因素决定?
3、双曲线能和坐标轴相交吗?为什么?
总结:
1、对双曲线,当k>0时,在每个象限内,x、y的增减情况相反;当k<0时,在每个象限内, x、y的增减情况相同。
2、当x的绝对值无限增大时,双曲线的两支无限接近x轴;当x的绝对值无限接近零时,双曲线的两支无限接近y轴,但永远不会与坐标轴相交。
回味无穷
反比例函数的性质:
1、反比例函数的图像
2、象限问题
3、增减性
4、对称性
5、趋向性
6、图像离原点的远近
例2:如果反比例函数图像经过A(-3,6)
(1)求这个反比例函数的表达式
(2)如果双曲线经过B(a,m),
C(b,n),
当a > b > 0,判断m,n的大小
当0 > a > b ,判断m,n的大小
当a> 0 > b ,判断m,n的大小
巩固练习:
1、课本P12随堂练习1-2;
P13习题1;4;5
2、细解巧练P4变式1-2;
变式7-8
想一想
在双曲线上任取两个点P、Q,过每个点分别向x、y轴做平行线,与坐标轴围城矩形的面积S1、S2,则S1、S2有什么关系?为什么?
巩固练习:
课本P13习题2
细解巧练P4变式3-4
x
y
o
x
y
o
应用:
1、函数 的图象在第 象限内,在每个象限内,y随x的增大而 。
2、若双曲线 , y随x的增大而增大,则k= 。
3、下面给出了反比例函数 和 的图象,你知道哪一个是 的图象吗?为什么?
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
提高从函数的图象中获取信息的能力
x
y
o
x
y
o
说一说,当你看到下面的图象时,你能从中知道些什么
x
y
o
x
y
o
x
y
o
y=kx+b
y=kx+b
七、超越自我
课外探索与交流:
在同一坐标系中,函数 和y=k2x+b的
图像大致如下,则 k1 、k2、b各应满足什么条件?说明理由。
A
B
C
D
知识的综合运用:
祝你成功!
由k<0可知,两个函数的图象在第二,四象限,故可选(2),(4);再由y=k(x-1)=kx-k得-k>0,即一次函数与y轴的正半轴相交,因此选(2).
观察与发现
想一想
x
y
o
x
y
o
x
y
o
x
y
o
(1) (2) (3) (4)
联系拓广
在同一坐标系内作出函数 与函数y=x-1的图象,并利用图像求它们的交点坐标.
●
●
y=x-1
●
●
●
●
●
●
●
●
●
●
(-1,-2)
(2,1)
思考:反比例函数与正比例函数图像一定有交点?什么情况下有交点?
巩固练习
1、课本习题P9
2、细解巧练P3变式1-2;当堂巩固
巩固练习
细解巧练P5变式5-6
反比例函数的图象与性质
“心动”不如行动
列表(在自变量取值勤范围内取一些值,并计算相应的函数值)
连线
做一做
驶向胜利的彼岸
描点
x -8 -4 -2 -1 1 2 4 8
-1
-2
-4
-8
8
4
2
1
x
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
.
y
x
-1
-2
-4
-8
8
4
2
1
x … -8 -4 -2 -1 … 1 2 4 8
… …
.
.
.
.
…
…
.
.
y = —
-4
x
驶向胜利的彼岸
“心动”不如行动
你认为作比例函数图象时应注意哪些问题?
列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;
列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线(平滑的曲线),又较准确地表达函数的变化趋势;
描点时一定要养成按自变量从小到大的顺序 依次画线,从中体会函数的增减性;
……
做一做
5
驶向胜利的彼岸
独立完成函数图像
y=
y=-
8
x
8
x
8
x
y=
8
x
y=
y
x
-6
-5
5
1
2
3
4
-8
-7
-4
-3
-2
-1
6
7
8
…
…
1
8/3
…
…
8/7
4/3
8/5
2
4
8
-8
-4
-8/3
-2
-8/5
-4/3
-8/7
-1
反比例函数的图象和性质
“行家”看门道
形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;
想一想
6
驶向胜利的彼岸
反比例函数的图象和性质
1、形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
2、位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内。
反比例函数 的图象和性质
y =
x
k
y
x
o
x
y
o
K>0
K<0
反比例函数的图象和性质
3、反比例函数图像双曲线的两个分支是轴对称图形,对称轴是直线y=x和直线y=-x两条,同时又是中心对称图形,对称中心是坐标原点o.
反比例函数 的图象和性质
y =
x
k
y
x
o
x
y
o
K>0
K<0
“双胞胎”之间的差异
y
x
o
x
y
o
下面给出了反比例函数 和
的图象,你能知道哪一个是 图象吗?为什么?
y=
-2
x
y=
2
x
y=
-2
x
“试金石”
随堂练习
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
1、反比例函数y= - 的图象大致是( )
D
活学活用
1.函数 的图像在第_____象限,函数 的图象在第 象限。
2. 双曲线 经过点(-3,___)
y =
x
5
y =
1
3x
3.函数 的图像在二、四象限,则m的取值范围是 ____ .
4.对于函数 ,这部分图像在第 ________象限.
y =
1
2x
m-2
x
y =
测一测
二,四
m < 2
一、三
9
1
一、三
例1:如图是反比例函数 的图像的一支
x
o
y
y=
m-6
x
⑴图像的另一只位于哪个象限?常数m的取值范围是什么?
⑵图像经过点(-2,6),判断
点A(-3,4),B(8,- )
C(4,-4)在图像上吗?
3
2
巩固练习;已知反比例函数y= (k≠0)的图象的一支如图。
(1)判断k是正数还是负数;
(2)求这个反比例函数的解析式;
(3)补画这个反比例函数图象的另一支。
y
x
y
0
(-4,2)
基础训练:
1.若y=(a-1)x a是反比例函数,则图象在 象限;
2. 已知变量y与x成反比例,当x=3时,y=-6;那么
当y=3时,x的值是 ;
3.已知点A(-2,a)在函数 的图像上,则 a= ;
4、若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________
k>-1
5、甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)的函数,则这个函数的图象大致是( )
C
在实际问题中图象就可能只有一支。
课内练习:
1、已知反比例函数 (k≠0) 的图象上一点的坐标为( ,2 )。
求这个反比例函数的解析式。
y =
x
k
2、已知y 与 x 成反比例, 并且当 x = 2 时, y = 5,求 x 与 y 的函数关系式。
3、根据图形写出函数的解析式。
y
x
y
0
(-3,1)
y =
x
3
x
10
y =
反比例函数性质
第二课时
y
x
o
x
y
o
观察图像解决一下问题:
1、判断双曲线的k的正负
2、在每个象限内,随着x的逐渐增大,y的变化有什么规律?要注意什么?有哪些因素决定?
3、双曲线能和坐标轴相交吗?为什么?
总结:
1、对双曲线,当k>0时,在每个象限内,x、y的增减情况相反;当k<0时,在每个象限内, x、y的增减情况相同。
2、当x的绝对值无限增大时,双曲线的两支无限接近x轴;当x的绝对值无限接近零时,双曲线的两支无限接近y轴,但永远不会与坐标轴相交。
回味无穷
反比例函数的性质:
1、反比例函数的图像
2、象限问题
3、增减性
4、对称性
5、趋向性
6、图像离原点的远近
例2:如果反比例函数图像经过A(-3,6)
(1)求这个反比例函数的表达式
(2)如果双曲线经过B(a,m),
C(b,n),
当a > b > 0,判断m,n的大小
当0 > a > b ,判断m,n的大小
当a> 0 > b ,判断m,n的大小
巩固练习:
1、课本P12随堂练习1-2;
P13习题1;4;5
2、细解巧练P4变式1-2;
变式7-8
想一想
在双曲线上任取两个点P、Q,过每个点分别向x、y轴做平行线,与坐标轴围城矩形的面积S1、S2,则S1、S2有什么关系?为什么?
巩固练习:
课本P13习题2
细解巧练P4变式3-4
x
y
o
x
y
o
应用:
1、函数 的图象在第 象限内,在每个象限内,y随x的增大而 。
2、若双曲线 , y随x的增大而增大,则k= 。
3、下面给出了反比例函数 和 的图象,你知道哪一个是 的图象吗?为什么?
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
提高从函数的图象中获取信息的能力
x
y
o
x
y
o
说一说,当你看到下面的图象时,你能从中知道些什么
x
y
o
x
y
o
x
y
o
y=kx+b
y=kx+b
七、超越自我
课外探索与交流:
在同一坐标系中,函数 和y=k2x+b的
图像大致如下,则 k1 、k2、b各应满足什么条件?说明理由。
A
B
C
D
知识的综合运用:
祝你成功!
由k<0可知,两个函数的图象在第二,四象限,故可选(2),(4);再由y=k(x-1)=kx-k得-k>0,即一次函数与y轴的正半轴相交,因此选(2).
观察与发现
想一想
x
y
o
x
y
o
x
y
o
x
y
o
(1) (2) (3) (4)
联系拓广
在同一坐标系内作出函数 与函数y=x-1的图象,并利用图像求它们的交点坐标.
●
●
y=x-1
●
●
●
●
●
●
●
●
●
●
(-1,-2)
(2,1)
思考:反比例函数与正比例函数图像一定有交点?什么情况下有交点?
巩固练习
1、课本习题P9
2、细解巧练P3变式1-2;当堂巩固
巩固练习
细解巧练P5变式5-6
