青岛版 数学六年级上册 比例法解决相遇问题(课件)(共27张PPT)
文档属性
| 名称 | 青岛版 数学六年级上册 比例法解决相遇问题(课件)(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 146.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 14:43:22 | ||
图片预览








文档简介
(共27张PPT)
比例法——
解决相遇问题
相遇问题:
路程和=速度和×相遇时间
时间相等,路程比与速度比成正比
基本原理:
知识点:
(一)一般的相遇问题
(二)距离中点若干米相遇
(三)多人相遇问题
(四)两人多次相遇问题
(五)同一地点出发,返回相遇问题
(六)速度变化的相遇问题
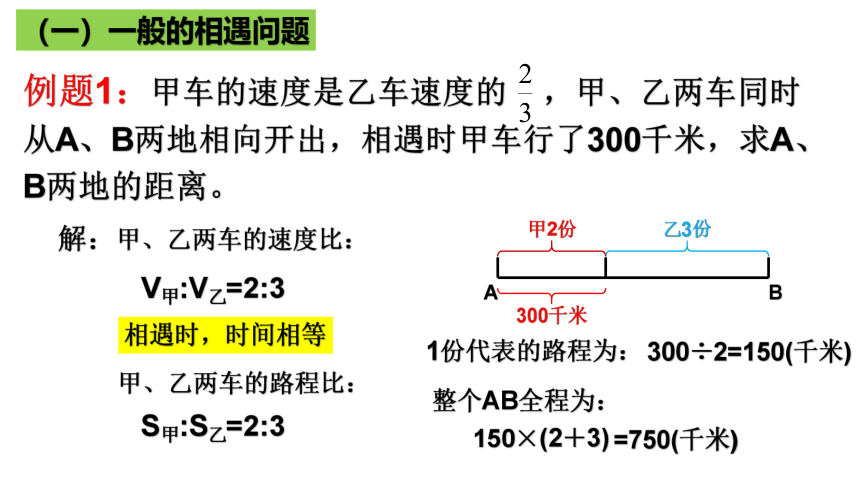
(一)一般的相遇问题
例题1:甲车的速度是乙车速度的 ,甲、乙两车同时
从A、B两地相向开出,相遇时甲车行了300千米,求A、
B两地的距离。
解:甲、乙两车的速度比:
V甲:V乙=2:3
相遇时,时间相等
S甲:S乙=2:3
甲、乙两车的路程比:
甲2份
乙3份
A
B
300千米
1份代表的路程为:
300÷2=150(千米)
整个AB全程为:
150×(2+3)
=750(千米)
练习1:甲车的速度是乙车速度的 ,甲、乙两车同时
从A、B两地相向开出,相遇时甲车行了96千米,求A、
B两地的距离。
练习2:甲车的速度是乙车速度的1.25倍,甲、乙两车
同时从A、B两地相向开出,相遇时甲车离B地还有320
千米,求A、B两地的距离。
例题2:从A城到B城,甲汽车用6小时,从B城到A城,
乙汽车用4小时。现在甲、乙两车分别从A、B两城同时
出发相对而行,相遇时甲车比乙车少走30千米,求A、B
两城的距离。
解:甲、乙两车的时间比:
t甲:t乙=6:4
=3:2
路程一定,
速度比与时间比成反比
V甲:V乙=2:3
相遇时,时间一定
甲、乙两车的路程比:
S甲:S乙=2:3
甲车比乙车少走的份数:
3-2=1份
1份就是30千米
A、B之间的全程为:
30×(2+3)
=150(千米)
练习1:一列快车从甲站到乙站需要8小时,一列慢车从
乙站到甲站需要12小时,两车同时从两站相对开出,相遇
时快车比慢车多行了48千米,甲、乙两站相距多少千米?
练习2:客车从甲地到乙地,要行5小时,货车从乙地到
甲地,每小时行90千米。现在客、货两车从甲、乙两地
同时相向而行,相遇时,客车与货车所行的路程比是4:3,
求甲、乙两地的距离是多少千米?
(二)距离中点若干米相遇
例题3:A、B两地之间有一条公路,大客车从A到B需要6小时,小客车要4小时。两车同时从A、B两地出发相向而行,在离中点24千米的地方相遇,求A、B两地的距离。
解:大、小客车的时间比:
t大:t小=6:4
= 3:2
V大:V小=2:3
相遇时,大、小客车的路程比:
S大:S小=2:3
大、小客车的速度比:
大车2份
小车3份
中点
2.5份
2.5份
24千米
A
B
A到中点的路程份数:
(2+3)÷2
=2.5份
24千米对应的份数为:
2.5-2=0.5份
A、B两地的距离为:
24÷0.5
×5
=240(千米)
练习1:甲、乙两车分别从A、B两地同时出发相向而
行,相遇点距中点24千米。已知甲车的速度是乙车的
62.5%,求A、B两地的距离。
练习2:快车、慢车分别从A、B两地,同时出发,相向
而行。已知快车、慢车的速度比是5:4,相遇时距两地的
中点24千米。相遇后,两车继续前行,当慢车行驶到两
地中点时,快车行驶了多少千米?
例题4:甲、乙、丙三人,甲每分钟走60米,乙每分钟走70米,丙每分钟走80米,甲、乙从A、丙从B同时出发相向而行,丙遇到乙后,经过10分钟遇到了甲,求A、B之间的距离。
(三)多人相遇问题
乙7份
丙8份
甲6份
A
D
C
B
甲
丙
丙
甲
乙
解:甲乙丙三人的速度比为:
V甲:V乙:V丙
=60:70:80
=6:7:8
乙与丙相遇在C点,甲走到D点,
时间相等,
路程比与速度比成正比
甲乙丙三人的路程比为:
=6:7:8
乙
甲与丙相遇,走的路程是CD长度
(60+80)×10
=1400(米)
CD的份数为:
7-6=1(份)
1份对应1400米
AB间的路程是:
1400×(7+8)
=21000(米)
S甲:S乙:S丙
练习1:甲、乙、丙三人,甲每分钟走20米,乙每分钟
走22.5米,丙每分钟走25米,甲、乙从东镇,丙从西镇
同时出发,丙遇到乙后再经过10分钟遇到甲,两镇相距
多少米?
练习2:甲、乙、丙三人的步行速度分别为每分钟70米、
60米和50米,甲从B地,乙和丙从A地同时出发相向而行,
途中甲遇到乙后10分钟又遇到丙,求A、B两地的距离。
(四)两人多次相遇问题
相遇1次,两人走的路程和为1个全程;
相遇2次,两人走的路程和为3个全程;
相遇3次,两人走的路程和为5个全程;
相遇4次,两人走的路程和为7个全程;
……,
……;
相遇N次,两人走的路程和为2N-1个全程。
例题5:甲、乙两人同时从A、B两地出发相向而行,甲的速度是乙的速度的1.5倍,到达对方的出发点后马上返回,如果第一次相遇点和第二次相遇点相距30千米,那么A、B两地相距多少千米?
解:甲乙的速度比是:
3:2
每次相遇,时间相等
甲乙的路程比是:
3:2
A
C
B
第一次相遇在C点,
一次
甲乙一起走了1个全程,
其中甲走了3份
第二次相遇,
甲乙一起走了3个全程,
甲走的份数为:
3×3
=9份
D
二次
30千米
CD的份数为:
2份
AB间的距离为:
30÷2×5
=75(千米)
甲
乙
相遇在D点,
练习1:甲、乙两人同时从A、B两地出发相向而行,第一次相遇后两人继续前进,到过对方的出发点后都立即返回,第二次相遇点与第一次相遇点相距2.4千米,若甲的速度是乙的 ,则A、B之间的距离为多少千米?
练习2:甲、乙两车分别从A、B两地出发,且在A、B之间不断的往返行驶,已知甲车的速度是15千米/小时,乙车的速度是25千米/小时,甲、乙两车第二次相遇的地点与第四次相遇的地点相差100千米,求A、B之间的距离。
例题6:甲、乙两车同时从A地开往B地,甲车到达B地后立即返回在离B地45千米处与乙车相遇。甲乙两车的速度比是3:2,求相遇时乙车行了多少千米?
45千米
甲比乙多走了:45×2 = 90千米
相遇时间一定,
速度比与路程比成正比
乙的路程:90÷(3-2)×2 = 180(千米)
答:相遇时乙车行了180千米。
A
B
甲与乙的路程比:
3:2
(五)同一地点出发,返回相遇问题
练习1:甲、乙两车同时从A地开往B地,甲车到达B地后立即返回在离B地30千米处与乙车相遇。甲乙两车的速度比是5:4,求相遇时乙车行了多少千米?
练习2:甲、乙两人同时骑车由相距60千米的A地到B地,甲每小时比乙每小时慢4千米,乙先到B地后立即返回,在距离B地12千米处与甲相遇。求甲的速度。
例题7:甲、乙两人骑自行车分别从A、B两地同时出发,相向而行,出发时甲与乙的速度比为3:2,相遇后甲的速度提高了20%,乙的速度提高了30%,这样当甲到达B地时,乙离A地还有14千米,求AB两地相距多少千米?
(六)速度变化的相遇问题
解:V甲 : V乙=3 : 2
提速后,V甲提 : V乙提
=[3×(1+20%)] : [2×(1+30%)]
=3.6 : 2.6
=18 : 13
时间相等,路程比与速度比成正比
相遇时,S甲 : S乙=3 : 2
提速后,S甲提 : S乙提=18 : 13
A
B
相遇
甲
乙
3份
2份
甲
乙
18份
13份
×9
×9
14份
14千米
乙离A地的份数为:
3×9-13=14份
AB两地相距:
14÷14×(18+27)
=45(千米)
练习1:甲、乙两车分别从A、B两地同时出发相向而行,出发时甲、乙的速度比是5:2,相遇后甲的速度减少60%,乙的速度减少了50%,当甲到达B地时,乙离A地还有40千米,求A、B两地的距地。
练习2:甲、乙两车分别从A、B两地出发,相向而行。出发时,甲、乙的速度比是5:4。相遇后,甲的速度减少20%,乙的速度增加20%,这样,当甲到达B地时,乙离A地还有10千米。那么A、B两地相距多少千米?
课后练习
1.A、B两地之间有一条公路,大客车从A到B需要6小时,小客车要4小时。两车同时从A、B两地出发相向而行,在离中点24千米的地方相遇,求A、B两地的距离。
2.甲、乙、丙三人,甲每分钟走60米,乙每分钟走70米,丙每分钟走80米,甲、乙从A、丙从B同时出发相向而行,丙遇到乙后,经过10分钟遇到了甲,求A、B之间的距离。
3.甲、乙两人同时从A、B两地出发相向而行,甲的速度是乙的速度的1.5倍,到达对方的出发点后马上返回,如果第一次相遇点和第二次相遇点相距40千米,那么A、B两地相距多少千米?
4.甲、乙两车同时从A地开往B地,甲车到达B地后立即返回在离B地45千米处与乙车相遇。甲乙两车的速度比是3:2,求AB两地相距多少千米?
比例法——
解决相遇问题
相遇问题:
路程和=速度和×相遇时间
时间相等,路程比与速度比成正比
基本原理:
知识点:
(一)一般的相遇问题
(二)距离中点若干米相遇
(三)多人相遇问题
(四)两人多次相遇问题
(五)同一地点出发,返回相遇问题
(六)速度变化的相遇问题
(一)一般的相遇问题
例题1:甲车的速度是乙车速度的 ,甲、乙两车同时
从A、B两地相向开出,相遇时甲车行了300千米,求A、
B两地的距离。
解:甲、乙两车的速度比:
V甲:V乙=2:3
相遇时,时间相等
S甲:S乙=2:3
甲、乙两车的路程比:
甲2份
乙3份
A
B
300千米
1份代表的路程为:
300÷2=150(千米)
整个AB全程为:
150×(2+3)
=750(千米)
练习1:甲车的速度是乙车速度的 ,甲、乙两车同时
从A、B两地相向开出,相遇时甲车行了96千米,求A、
B两地的距离。
练习2:甲车的速度是乙车速度的1.25倍,甲、乙两车
同时从A、B两地相向开出,相遇时甲车离B地还有320
千米,求A、B两地的距离。
例题2:从A城到B城,甲汽车用6小时,从B城到A城,
乙汽车用4小时。现在甲、乙两车分别从A、B两城同时
出发相对而行,相遇时甲车比乙车少走30千米,求A、B
两城的距离。
解:甲、乙两车的时间比:
t甲:t乙=6:4
=3:2
路程一定,
速度比与时间比成反比
V甲:V乙=2:3
相遇时,时间一定
甲、乙两车的路程比:
S甲:S乙=2:3
甲车比乙车少走的份数:
3-2=1份
1份就是30千米
A、B之间的全程为:
30×(2+3)
=150(千米)
练习1:一列快车从甲站到乙站需要8小时,一列慢车从
乙站到甲站需要12小时,两车同时从两站相对开出,相遇
时快车比慢车多行了48千米,甲、乙两站相距多少千米?
练习2:客车从甲地到乙地,要行5小时,货车从乙地到
甲地,每小时行90千米。现在客、货两车从甲、乙两地
同时相向而行,相遇时,客车与货车所行的路程比是4:3,
求甲、乙两地的距离是多少千米?
(二)距离中点若干米相遇
例题3:A、B两地之间有一条公路,大客车从A到B需要6小时,小客车要4小时。两车同时从A、B两地出发相向而行,在离中点24千米的地方相遇,求A、B两地的距离。
解:大、小客车的时间比:
t大:t小=6:4
= 3:2
V大:V小=2:3
相遇时,大、小客车的路程比:
S大:S小=2:3
大、小客车的速度比:
大车2份
小车3份
中点
2.5份
2.5份
24千米
A
B
A到中点的路程份数:
(2+3)÷2
=2.5份
24千米对应的份数为:
2.5-2=0.5份
A、B两地的距离为:
24÷0.5
×5
=240(千米)
练习1:甲、乙两车分别从A、B两地同时出发相向而
行,相遇点距中点24千米。已知甲车的速度是乙车的
62.5%,求A、B两地的距离。
练习2:快车、慢车分别从A、B两地,同时出发,相向
而行。已知快车、慢车的速度比是5:4,相遇时距两地的
中点24千米。相遇后,两车继续前行,当慢车行驶到两
地中点时,快车行驶了多少千米?
例题4:甲、乙、丙三人,甲每分钟走60米,乙每分钟走70米,丙每分钟走80米,甲、乙从A、丙从B同时出发相向而行,丙遇到乙后,经过10分钟遇到了甲,求A、B之间的距离。
(三)多人相遇问题
乙7份
丙8份
甲6份
A
D
C
B
甲
丙
丙
甲
乙
解:甲乙丙三人的速度比为:
V甲:V乙:V丙
=60:70:80
=6:7:8
乙与丙相遇在C点,甲走到D点,
时间相等,
路程比与速度比成正比
甲乙丙三人的路程比为:
=6:7:8
乙
甲与丙相遇,走的路程是CD长度
(60+80)×10
=1400(米)
CD的份数为:
7-6=1(份)
1份对应1400米
AB间的路程是:
1400×(7+8)
=21000(米)
S甲:S乙:S丙
练习1:甲、乙、丙三人,甲每分钟走20米,乙每分钟
走22.5米,丙每分钟走25米,甲、乙从东镇,丙从西镇
同时出发,丙遇到乙后再经过10分钟遇到甲,两镇相距
多少米?
练习2:甲、乙、丙三人的步行速度分别为每分钟70米、
60米和50米,甲从B地,乙和丙从A地同时出发相向而行,
途中甲遇到乙后10分钟又遇到丙,求A、B两地的距离。
(四)两人多次相遇问题
相遇1次,两人走的路程和为1个全程;
相遇2次,两人走的路程和为3个全程;
相遇3次,两人走的路程和为5个全程;
相遇4次,两人走的路程和为7个全程;
……,
……;
相遇N次,两人走的路程和为2N-1个全程。
例题5:甲、乙两人同时从A、B两地出发相向而行,甲的速度是乙的速度的1.5倍,到达对方的出发点后马上返回,如果第一次相遇点和第二次相遇点相距30千米,那么A、B两地相距多少千米?
解:甲乙的速度比是:
3:2
每次相遇,时间相等
甲乙的路程比是:
3:2
A
C
B
第一次相遇在C点,
一次
甲乙一起走了1个全程,
其中甲走了3份
第二次相遇,
甲乙一起走了3个全程,
甲走的份数为:
3×3
=9份
D
二次
30千米
CD的份数为:
2份
AB间的距离为:
30÷2×5
=75(千米)
甲
乙
相遇在D点,
练习1:甲、乙两人同时从A、B两地出发相向而行,第一次相遇后两人继续前进,到过对方的出发点后都立即返回,第二次相遇点与第一次相遇点相距2.4千米,若甲的速度是乙的 ,则A、B之间的距离为多少千米?
练习2:甲、乙两车分别从A、B两地出发,且在A、B之间不断的往返行驶,已知甲车的速度是15千米/小时,乙车的速度是25千米/小时,甲、乙两车第二次相遇的地点与第四次相遇的地点相差100千米,求A、B之间的距离。
例题6:甲、乙两车同时从A地开往B地,甲车到达B地后立即返回在离B地45千米处与乙车相遇。甲乙两车的速度比是3:2,求相遇时乙车行了多少千米?
45千米
甲比乙多走了:45×2 = 90千米
相遇时间一定,
速度比与路程比成正比
乙的路程:90÷(3-2)×2 = 180(千米)
答:相遇时乙车行了180千米。
A
B
甲与乙的路程比:
3:2
(五)同一地点出发,返回相遇问题
练习1:甲、乙两车同时从A地开往B地,甲车到达B地后立即返回在离B地30千米处与乙车相遇。甲乙两车的速度比是5:4,求相遇时乙车行了多少千米?
练习2:甲、乙两人同时骑车由相距60千米的A地到B地,甲每小时比乙每小时慢4千米,乙先到B地后立即返回,在距离B地12千米处与甲相遇。求甲的速度。
例题7:甲、乙两人骑自行车分别从A、B两地同时出发,相向而行,出发时甲与乙的速度比为3:2,相遇后甲的速度提高了20%,乙的速度提高了30%,这样当甲到达B地时,乙离A地还有14千米,求AB两地相距多少千米?
(六)速度变化的相遇问题
解:V甲 : V乙=3 : 2
提速后,V甲提 : V乙提
=[3×(1+20%)] : [2×(1+30%)]
=3.6 : 2.6
=18 : 13
时间相等,路程比与速度比成正比
相遇时,S甲 : S乙=3 : 2
提速后,S甲提 : S乙提=18 : 13
A
B
相遇
甲
乙
3份
2份
甲
乙
18份
13份
×9
×9
14份
14千米
乙离A地的份数为:
3×9-13=14份
AB两地相距:
14÷14×(18+27)
=45(千米)
练习1:甲、乙两车分别从A、B两地同时出发相向而行,出发时甲、乙的速度比是5:2,相遇后甲的速度减少60%,乙的速度减少了50%,当甲到达B地时,乙离A地还有40千米,求A、B两地的距地。
练习2:甲、乙两车分别从A、B两地出发,相向而行。出发时,甲、乙的速度比是5:4。相遇后,甲的速度减少20%,乙的速度增加20%,这样,当甲到达B地时,乙离A地还有10千米。那么A、B两地相距多少千米?
课后练习
1.A、B两地之间有一条公路,大客车从A到B需要6小时,小客车要4小时。两车同时从A、B两地出发相向而行,在离中点24千米的地方相遇,求A、B两地的距离。
2.甲、乙、丙三人,甲每分钟走60米,乙每分钟走70米,丙每分钟走80米,甲、乙从A、丙从B同时出发相向而行,丙遇到乙后,经过10分钟遇到了甲,求A、B之间的距离。
3.甲、乙两人同时从A、B两地出发相向而行,甲的速度是乙的速度的1.5倍,到达对方的出发点后马上返回,如果第一次相遇点和第二次相遇点相距40千米,那么A、B两地相距多少千米?
4.甲、乙两车同时从A地开往B地,甲车到达B地后立即返回在离B地45千米处与乙车相遇。甲乙两车的速度比是3:2,求AB两地相距多少千米?
