苏科版九年级数学上册 1.4 用一元二次方程解决问题(共15张)
文档属性
| 名称 | 苏科版九年级数学上册 1.4 用一元二次方程解决问题(共15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
1.4 用一元二次方程解决问题
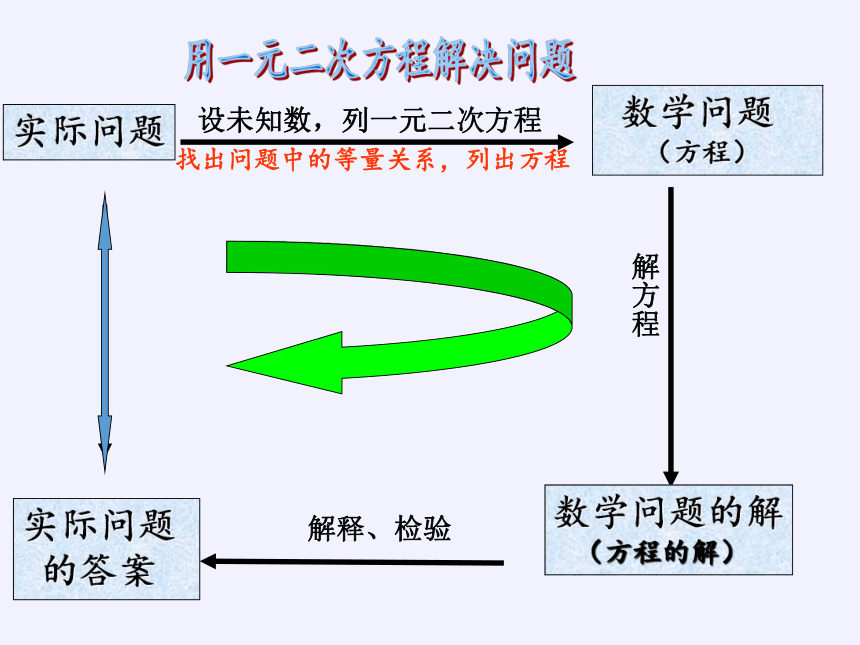
实际问题
设未知数,列一元二次方程
数学问题
(方程)
解方程
数学问题的解
(方程的解)
解释、检验
实际问题
的答案
用一元二次方程解决问题
找出问题中的等量关系,列出方程
列方程解应用题的一般步骤:
◆ 1.审:审清题意:已知什么,求什么,已知、未知之间有什么关系;
◆ 2.设:设未知数,语句要完整,有单位的要注明单位;
◆ 3.找:找出等量关系;
◆ 4.列:根据等量关系列代数式、列方程;
◆ 5.解:解所列的方程;
◆ 6.验:是否是所列方程的解、是否符合题意;
◆ 7.答:答案也必需是完整的语句,注明单位.
二、列方程解应用题的关键是:
◆找:找出等量关系.
【常见类型】
用一元二次方程解决实际问题的常见类型:
◆增长率问题
◆面积问题
◆决策问题
◆数字问题
◆面积问题
用一元二次方程解决实际问题:
面积问题
问题1 已知如图所示的图形的面积为24,根据图中的条件,可列出方程: .
分形、补形
面积问题
变式 如图所示,在长和宽分别是a、b的矩形纸片的四个角都
剪去一个边长为x的正方形.
(1)用a,b,x表示纸片剩余部分的
面积;
(2)当a=6,b=4,且剪去部分的面积
等于剩余部分的面积时,求正方形的边长.
(2)依题意有:
将a=6,b=4,代入上式,得
解得
解:(1) ;
即正方形的边长为 .
面积问题
问题2 如图,在长为100米,宽为80米的矩形场地上修建两条
宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面
积为7644米2,则道路的宽应为多少米?设道路的宽为x米,则
可列方程为( )
A.100×80-100x-80x=7644 B.(100-x)(80-x)+x2=7644
C.(100-x)(80-x)=7644 D.100x+80x=356
100米
80
米
80
米
100米
80
米
100米
C
100m
80m
面积问题
100m
80m
100m
80m
100m
80m
改为折线又如何?
80m
100m
80m
100m
改为曲线又如何?
面积问题
平移、切割拼接
面积问题
变式1 一幅长20cm、宽12cm的图案,如图,其中有一横两
竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为
xcm,图案中三条彩条所占面积为ycm2.
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的 ,求横、竖
彩条的宽度.
解:(1)根据题意可知::设横彩条的宽度为xcm,
xcm,
则横彩条的宽度为
∴y=20× x+2×12 x﹣2× x x
即y与x之间的函数关系式为y =﹣3x+54 x
(2)根据题意,得:﹣3x2+ 54x = ×20×12
整理,得:x2﹣18x+32=0,
解得:x1=2,x2=16(舍),
答:横彩条的宽度为3cm,竖彩条的宽度为2cm.
面积问题
变式2 为响应市委市政府提出的建设“绿色港城”的号召,我
市某单位准备将院内一块长30m,宽20m的长方形空地,建成一
个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的
小道,剩余的地方种植花草.如图所示,要使种植花草的面积
为532m2,那么小道进出口的宽度应为多少米?(注:所有小道
进出口的宽度相等,且每段小道均为平行四边形)
30m
20m
(30–2x)(20–x)=532
解:设小道进出口的宽度应为x米.
面积问题
学生练习: 小明家有一块长8 m、6 m的矩形空地,准备
在该空地上建造一个花园,并使花园面积为空地面积的一半,
小明设计了如下的四种方案,帮小明求出图中的各个x值.
方案一
方案二
方案三
方案四
实际问题
设未知数,列一元二次方程
数学问题
(方程)
解方程
数学问题的解
(方程的解)
解释、检验
实际问题
的答案
用一元二次方程解决问题
找出问题中的等量关系,列出方程
课堂总结:
谢 谢
1.4 用一元二次方程解决问题
实际问题
设未知数,列一元二次方程
数学问题
(方程)
解方程
数学问题的解
(方程的解)
解释、检验
实际问题
的答案
用一元二次方程解决问题
找出问题中的等量关系,列出方程
列方程解应用题的一般步骤:
◆ 1.审:审清题意:已知什么,求什么,已知、未知之间有什么关系;
◆ 2.设:设未知数,语句要完整,有单位的要注明单位;
◆ 3.找:找出等量关系;
◆ 4.列:根据等量关系列代数式、列方程;
◆ 5.解:解所列的方程;
◆ 6.验:是否是所列方程的解、是否符合题意;
◆ 7.答:答案也必需是完整的语句,注明单位.
二、列方程解应用题的关键是:
◆找:找出等量关系.
【常见类型】
用一元二次方程解决实际问题的常见类型:
◆增长率问题
◆面积问题
◆决策问题
◆数字问题
◆面积问题
用一元二次方程解决实际问题:
面积问题
问题1 已知如图所示的图形的面积为24,根据图中的条件,可列出方程: .
分形、补形
面积问题
变式 如图所示,在长和宽分别是a、b的矩形纸片的四个角都
剪去一个边长为x的正方形.
(1)用a,b,x表示纸片剩余部分的
面积;
(2)当a=6,b=4,且剪去部分的面积
等于剩余部分的面积时,求正方形的边长.
(2)依题意有:
将a=6,b=4,代入上式,得
解得
解:(1) ;
即正方形的边长为 .
面积问题
问题2 如图,在长为100米,宽为80米的矩形场地上修建两条
宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面
积为7644米2,则道路的宽应为多少米?设道路的宽为x米,则
可列方程为( )
A.100×80-100x-80x=7644 B.(100-x)(80-x)+x2=7644
C.(100-x)(80-x)=7644 D.100x+80x=356
100米
80
米
80
米
100米
80
米
100米
C
100m
80m
面积问题
100m
80m
100m
80m
100m
80m
改为折线又如何?
80m
100m
80m
100m
改为曲线又如何?
面积问题
平移、切割拼接
面积问题
变式1 一幅长20cm、宽12cm的图案,如图,其中有一横两
竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为
xcm,图案中三条彩条所占面积为ycm2.
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的 ,求横、竖
彩条的宽度.
解:(1)根据题意可知::设横彩条的宽度为xcm,
xcm,
则横彩条的宽度为
∴y=20× x+2×12 x﹣2× x x
即y与x之间的函数关系式为y =﹣3x+54 x
(2)根据题意,得:﹣3x2+ 54x = ×20×12
整理,得:x2﹣18x+32=0,
解得:x1=2,x2=16(舍),
答:横彩条的宽度为3cm,竖彩条的宽度为2cm.
面积问题
变式2 为响应市委市政府提出的建设“绿色港城”的号召,我
市某单位准备将院内一块长30m,宽20m的长方形空地,建成一
个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的
小道,剩余的地方种植花草.如图所示,要使种植花草的面积
为532m2,那么小道进出口的宽度应为多少米?(注:所有小道
进出口的宽度相等,且每段小道均为平行四边形)
30m
20m
(30–2x)(20–x)=532
解:设小道进出口的宽度应为x米.
面积问题
学生练习: 小明家有一块长8 m、6 m的矩形空地,准备
在该空地上建造一个花园,并使花园面积为空地面积的一半,
小明设计了如下的四种方案,帮小明求出图中的各个x值.
方案一
方案二
方案三
方案四
实际问题
设未知数,列一元二次方程
数学问题
(方程)
解方程
数学问题的解
(方程的解)
解释、检验
实际问题
的答案
用一元二次方程解决问题
找出问题中的等量关系,列出方程
课堂总结:
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
