苏科版九年级数学上册 2.2 圆的对称性(共24张)
文档属性
| 名称 | 苏科版九年级数学上册 2.2 圆的对称性(共24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 598.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
2.2 圆的对称性
圆的对称性
驶向胜利的彼岸
●O
圆是中心对称图形码?它的对称中心是什么?
圆是轴对称图形吗?它的对称轴是什么?
圆是中心对称图形,圆心是对称中心;
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴.
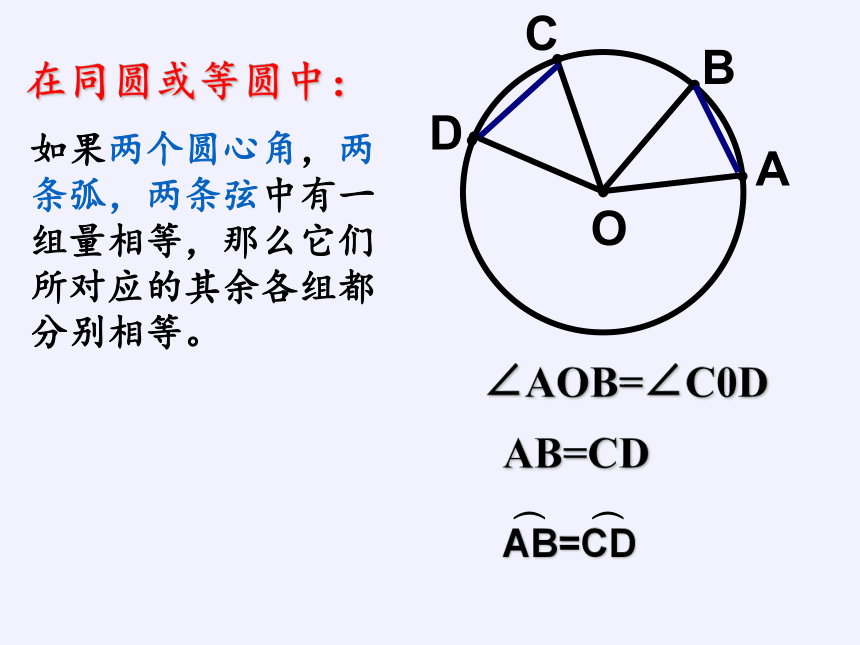
在同圆或等圆中:
∠AOB=∠C0D
AB=CD
AB=CD
)
)
如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等。
情景:你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳和智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
圆的对称性
·
如图圆形纸片, CD是⊙O直径.
1.在⊙O上任取一点A,过点A作直径CD的垂线,交⊙O于点B,点P为垂足.
2. 将圆沿着直径CD对折,你有什么发现呢?
●O
B
A
D
C
P
发现:CP=DP,弧AD=弧BD,弧AC=弧BC。
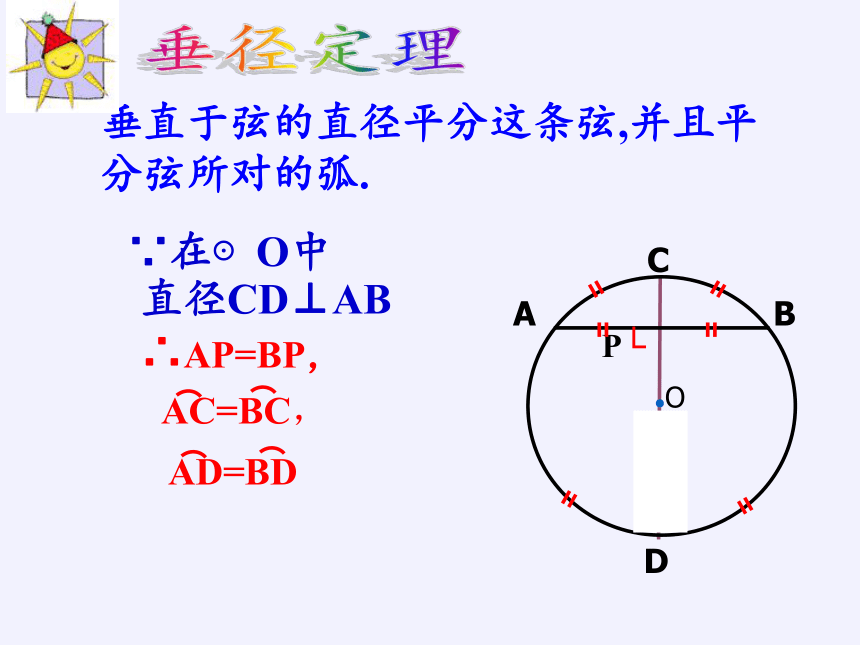
AC=BC,
AD=BD
∴AP=BP,
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
●O
A
B
C
D
P└
直径CD⊥AB
垂径定理
∵在⊙O中
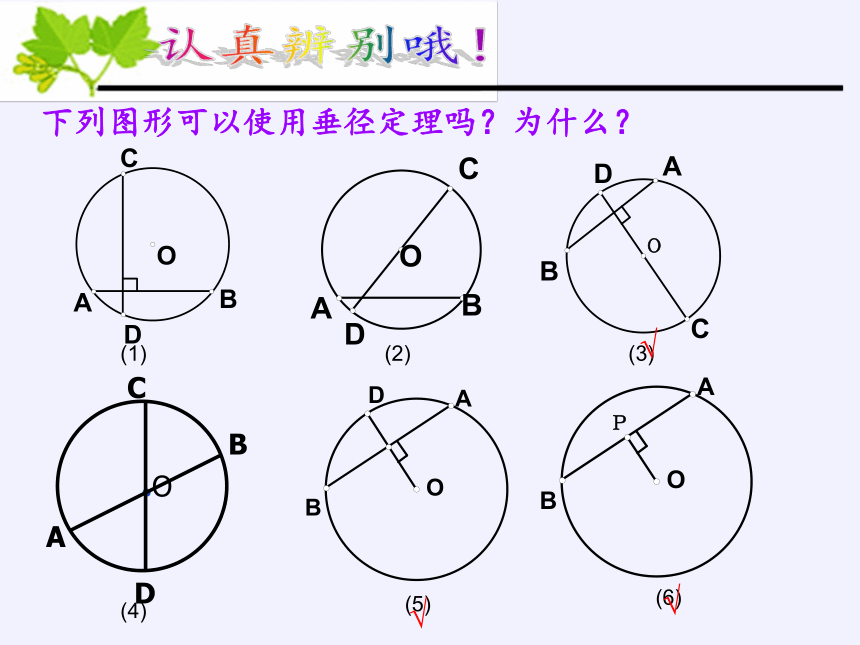
下列图形可以使用垂径定理吗?为什么?
认真辨别哦!
●O
A
B
C
D
O
P
(1)
(4)
(5)
(6)
(3)
(2)
√
√
√
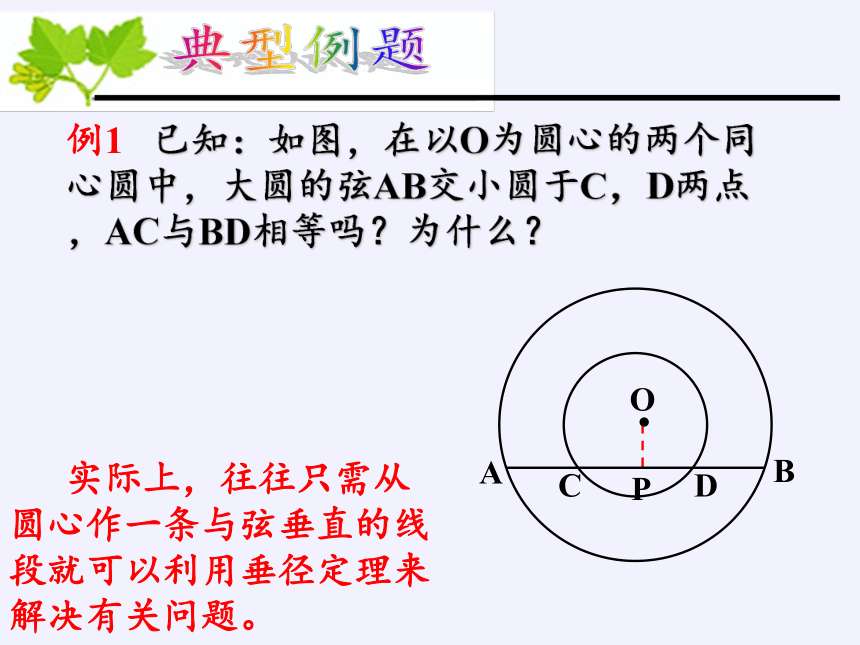
例1 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点,AC与BD相等吗?为什么?
P
.
A
C
D
B
O
典型例题
实际上,往往只需从圆心作一条与弦垂直的线段就可以利用垂径定理来解决有关问题。
⌒
⌒
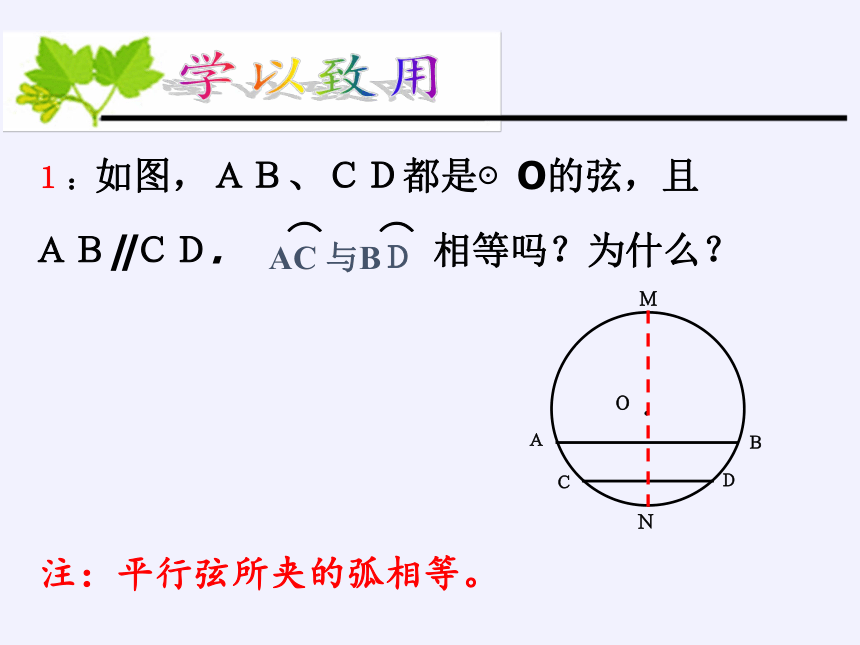
AC 与BD
1:如图,AB、CD都是⊙O的弦,且
AB‖CD. 相等吗?为什么?
.
O
C
B
A
D
学以致用
M
N
注:平行弦所夹的弧相等。
例2如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。
.
A
B
O
E
4
3
5
典型例题
学以至用
2.你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳和智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?(精确到0.1)
.
A
D
C
B
O
3.如图,在半径为13的⊙O中,OC垂直弦AB于点B,交⊙O于点C,AB=24,则CD的长为______。
学以致用
●O
A
D
C
B
7
4:如图, ⊙O的弦AB=8 ㎝ , DC=2㎝,直径CE⊥AB于D, 则半径OC=______。
学以致用
5
x
4
x-2
2
如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为_______.
3
5
挑战自我
例4:已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。
A
B
.
O
C
D
20
15
25
25
24
7
.
A
E
B
O
C
D
F
E
F
?
?
EF=15+7=22cm
或 EF=15-7=8cm
两条平行弦的相对位置有两种:圆心同侧
圆心异侧
典型例题
垂径定理的应用
5.在横截面为圆形的油槽内装入一些油后,若油面宽AB = 600mm,圆的直径为650mm,求油的最大深度.
E
D
600
B
A
O
600
650
E
F
挑战自我
C
D
课堂小结
图3
谈谈你今天的收获是什么?
解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,从而为应用垂径定理创造条件.
.
A
B
O
1.圆是轴对称图形.过圆心的任意一条直线都是它的对称轴.
2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
●O
2 . 已知AB和CD是⊙O内的两条弦,且AB∥CD,AB=6cm,CD =8cm,⊙O的半径为5cm,则弦AB和 弦CD的距离为__________.
分析:如图所示,AB,CD这两条弦在圆中位置有两种情况:(1)两条平行弦在圆心O的同侧;
(2)两条平行弦在圆心的O异侧;
.o
A
B
C
D
.o
A
B
C
D
E┘
┘F
┑F
┘E
2.如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
A
B
挑战自我
已知:C、D是弦AB上的两点,OC=OD,
求证:AC=BD
动脑想想吧!
E
如图,M为⊙O内的一点,利用尺规过点M作一条最短的弦,一条最长的弦 。
●O
●M
动脑想想吧!
A
B
C
D
∟
.银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如下图所示,污水水面宽度为60 cm,水面至管道顶部距离为10 cm,问修理人员应准备内径多大的管道
你学会了吗?
O
C
D
谢 谢
2.2 圆的对称性
圆的对称性
驶向胜利的彼岸
●O
圆是中心对称图形码?它的对称中心是什么?
圆是轴对称图形吗?它的对称轴是什么?
圆是中心对称图形,圆心是对称中心;
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴.
在同圆或等圆中:
∠AOB=∠C0D
AB=CD
AB=CD
)
)
如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等。
情景:你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳和智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
圆的对称性
·
如图圆形纸片, CD是⊙O直径.
1.在⊙O上任取一点A,过点A作直径CD的垂线,交⊙O于点B,点P为垂足.
2. 将圆沿着直径CD对折,你有什么发现呢?
●O
B
A
D
C
P
发现:CP=DP,弧AD=弧BD,弧AC=弧BC。
AC=BC,
AD=BD
∴AP=BP,
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
●O
A
B
C
D
P└
直径CD⊥AB
垂径定理
∵在⊙O中
下列图形可以使用垂径定理吗?为什么?
认真辨别哦!
●O
A
B
C
D
O
P
(1)
(4)
(5)
(6)
(3)
(2)
√
√
√
例1 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点,AC与BD相等吗?为什么?
P
.
A
C
D
B
O
典型例题
实际上,往往只需从圆心作一条与弦垂直的线段就可以利用垂径定理来解决有关问题。
⌒
⌒
AC 与BD
1:如图,AB、CD都是⊙O的弦,且
AB‖CD. 相等吗?为什么?
.
O
C
B
A
D
学以致用
M
N
注:平行弦所夹的弧相等。
例2如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。
.
A
B
O
E
4
3
5
典型例题
学以至用
2.你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳和智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?(精确到0.1)
.
A
D
C
B
O
3.如图,在半径为13的⊙O中,OC垂直弦AB于点B,交⊙O于点C,AB=24,则CD的长为______。
学以致用
●O
A
D
C
B
7
4:如图, ⊙O的弦AB=8 ㎝ , DC=2㎝,直径CE⊥AB于D, 则半径OC=______。
学以致用
5
x
4
x-2
2
如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为_______.
3
5
挑战自我
例4:已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。
A
B
.
O
C
D
20
15
25
25
24
7
.
A
E
B
O
C
D
F
E
F
?
?
EF=15+7=22cm
或 EF=15-7=8cm
两条平行弦的相对位置有两种:圆心同侧
圆心异侧
典型例题
垂径定理的应用
5.在横截面为圆形的油槽内装入一些油后,若油面宽AB = 600mm,圆的直径为650mm,求油的最大深度.
E
D
600
B
A
O
600
650
E
F
挑战自我
C
D
课堂小结
图3
谈谈你今天的收获是什么?
解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,从而为应用垂径定理创造条件.
.
A
B
O
1.圆是轴对称图形.过圆心的任意一条直线都是它的对称轴.
2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
●O
2 . 已知AB和CD是⊙O内的两条弦,且AB∥CD,AB=6cm,CD =8cm,⊙O的半径为5cm,则弦AB和 弦CD的距离为__________.
分析:如图所示,AB,CD这两条弦在圆中位置有两种情况:(1)两条平行弦在圆心O的同侧;
(2)两条平行弦在圆心的O异侧;
.o
A
B
C
D
.o
A
B
C
D
E┘
┘F
┑F
┘E
2.如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
A
B
挑战自我
已知:C、D是弦AB上的两点,OC=OD,
求证:AC=BD
动脑想想吧!
E
如图,M为⊙O内的一点,利用尺规过点M作一条最短的弦,一条最长的弦 。
●O
●M
动脑想想吧!
A
B
C
D
∟
.银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如下图所示,污水水面宽度为60 cm,水面至管道顶部距离为10 cm,问修理人员应准备内径多大的管道
你学会了吗?
O
C
D
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
