第四章图形的相似 单元测试训练卷 2021-2022学年北师版九年级数学上册(Word版含答案)
文档属性
| 名称 | 第四章图形的相似 单元测试训练卷 2021-2022学年北师版九年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 172.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 11:59:01 | ||
图片预览


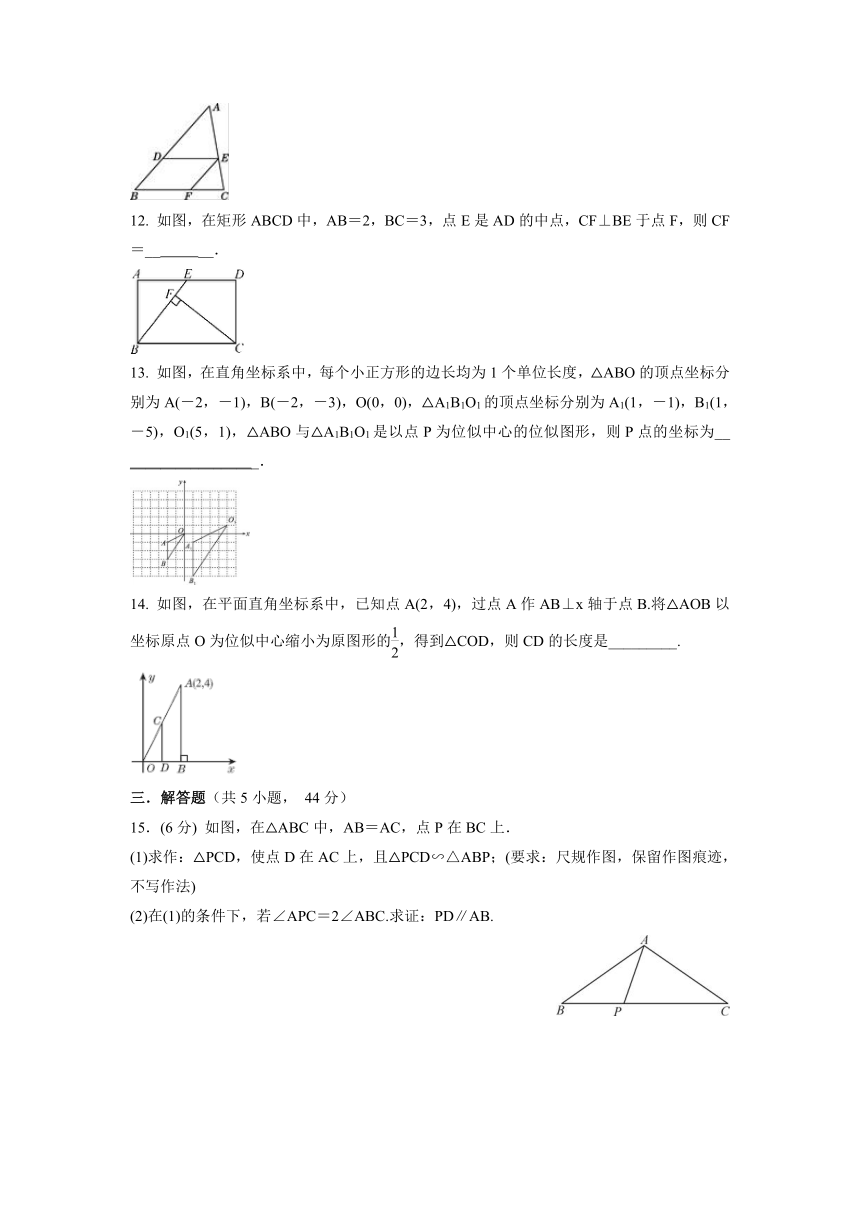
文档简介
北师版九年级数学上册
第四章 图形的相似
单元测试训练卷
一、选择题(共8小题,4*8=32)
1. 下列长度的各组线段中,成比例线段的是( )
A.1 cm,2 cm,3 cm,4 cm
B.1 cm,2 cm,3 cm,6 cm
C.2 cm,4 cm,6 cm,8 cm
D.3 cm,4 cm,5 cm,10 cm
2. 如图,直线a,b,c分别与直线m,n交于点A,B,C,D,E,F.已知直线a∥b∥c,若AB=2,BC=3,则的值为( )
A. B. C. D.
3. 如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,那么与△ABC相似的三角形的个数有( )
A.1个 B.2个 C.3个 D.4个
4. 如图,在△ABC中,AC=2,BC=4,D为BC边上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为( )
A.2a B.a C.3a D.a
5. 如图,在 ABCD中,F为BC中点,延长AD至点E,使DE∶AD=1∶3,连接EF交DC于点G,则S△DEG:S△CFG=( )
A.2∶3 B.3∶2 C.9∶4 D.4∶9
6. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.57.5尺 C.6.25尺 D.56.5尺
7. 已知两点A(5,6),B(7,2),先将线段AB向左平移1个单位长度,再以原点O为位似中心,在第一象限内将其缩小为原来的得到线段CD,则点A的对应点C的坐标为( )
A.(2,3) B.(3,1) C.(2,1) D.(3,3)
8. 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列结论:①=;②=;③=;④=. 其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,4*6=24)
9.已知a,b满足=,则的值为_______.
10. 生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2 m,则a约为_________.
11. 如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为________.
12. 如图,在矩形ABCD中,AB=2,BC=3,点E是AD的中点,CF⊥BE于点F,则CF=__ __.
13. 如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为__ _________________.
14. 如图,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,则CD的长度是_________.
三.解答题(共5小题, 44分)
15.(6分) 如图,在△ABC中,AB=AC,点P在BC上.
(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠APC=2∠ABC.求证:PD∥AB.
16.(8分) 如图,在△ABC和△ADE中,==,点B,D,E在一条直线上,求证:△ABD∽△ACE.
17.(8分) 如图所示,三个边长为1个单位长度的正方形ABCD,ABEF,EFGH拼在一起.
(1)请找岀中相似的两个三角形,并证明;
(2)直接写出∠1,∠2,∠3这三个角度数之和.
18.(10分) 如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
(1)求证:GD·AB=DF·BG;
(2)连接CF,求证:∠CFB=45°.
19.(12分) 如图,在 ABCD中,DE⊥AC于点O,交BC于点E,EG=EC,GF∥AD交DE于点F,连接FC,点H为线段AO上一点,连接HD,HF.
(1)判断四边形GECF的形状,并说明理由;
(2)当∠DHF=∠HAD时,求证:AH·CH=EC·AD.
参考答案
1-4BADC 5-8DBAC
9. 10.1.24 m 11. 12. 13.(-5,-1) 14.2
15.解:(1)如图:作出∠APD=∠ABP,即可得到△PCD∽△ABP
(2)如图,∵∠APC=2∠ABC,∠APD=∠ABC,∴∠DPC=∠ABC,∴PD∥AB
16.证明:∵在△ABC和△ADE中, ==,∴△ABC∽△ADE,∴∠BAC=∠DAE,∴∠BAD=∠CAE,∵=,∴=,∴△ABD∽△ACE
17.解:(1)ACF∽ΔAHC.理由如下:∵AC=,AF=1,AH=2,∴==,而∠FAC=∠CAH,∴△ACF∽△AHC
(2)∵△ACF∽△AHC,∴∠2=∠ACH,而∠1=∠ACH+∠3,∴∠1=∠2+∠3.∵∠1=45°,∴∠1+∠2+∠3=90°
18.证明:(1)∵四边形ABCD是正方形∴∠BCD=∠ADC=90°,AB=BC,∵BF⊥DE,∴∠GFD=90°,∴∠BCD=∠GFD,∵∠BGC=∠FGD,∴△BGC∽△DGF,∴=,∴DG·BC=DF·BG,∵AB=BC,∴DG·AB=DF·BG
(2)连接BD,CF,∵△BGC∽△DGF,∴=,∴=,又∵∠BGD=∠CGF,∴△BGD∽△CGF,∴∠BDG=∠CFG,∵四边形ABCD是正方形,BD是对角线,∴∠BDG=∠ADC=45°,∴∠CFB=45°
19. 解:(1)四边形GECF是菱形,∵EG=EC,DE⊥AC,∴GO=CO,∵GF∥AD,AD∥BC,∴GF∥BC,∴∠FGO=∠ECO,∠GFO=∠CEO,∴△GFO≌△CEO(AAS),∴GF=EC,∴四边形GECF是平行四边形,又∵EG=EC,∴平行四边形GECF是菱形
(2)∵∠DHC=∠DAH+∠ADH=∠DHF+∠FHC,∠DHF=∠HAD,∴∠ADH=∠FHC,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAH=∠ACB,∵四边形GECF是菱形,∴EC=CF,∠HCF=∠ACB,∴∠HCF=∠DAH,∴△ADH∽△CHF,∴=,AH·CH=EC·AD
第四章 图形的相似
单元测试训练卷
一、选择题(共8小题,4*8=32)
1. 下列长度的各组线段中,成比例线段的是( )
A.1 cm,2 cm,3 cm,4 cm
B.1 cm,2 cm,3 cm,6 cm
C.2 cm,4 cm,6 cm,8 cm
D.3 cm,4 cm,5 cm,10 cm
2. 如图,直线a,b,c分别与直线m,n交于点A,B,C,D,E,F.已知直线a∥b∥c,若AB=2,BC=3,则的值为( )
A. B. C. D.
3. 如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,那么与△ABC相似的三角形的个数有( )
A.1个 B.2个 C.3个 D.4个
4. 如图,在△ABC中,AC=2,BC=4,D为BC边上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为( )
A.2a B.a C.3a D.a
5. 如图,在 ABCD中,F为BC中点,延长AD至点E,使DE∶AD=1∶3,连接EF交DC于点G,则S△DEG:S△CFG=( )
A.2∶3 B.3∶2 C.9∶4 D.4∶9
6. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.57.5尺 C.6.25尺 D.56.5尺
7. 已知两点A(5,6),B(7,2),先将线段AB向左平移1个单位长度,再以原点O为位似中心,在第一象限内将其缩小为原来的得到线段CD,则点A的对应点C的坐标为( )
A.(2,3) B.(3,1) C.(2,1) D.(3,3)
8. 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列结论:①=;②=;③=;④=. 其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,4*6=24)
9.已知a,b满足=,则的值为_______.
10. 生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2 m,则a约为_________.
11. 如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为________.
12. 如图,在矩形ABCD中,AB=2,BC=3,点E是AD的中点,CF⊥BE于点F,则CF=__ __.
13. 如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为__ _________________.
14. 如图,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,则CD的长度是_________.
三.解答题(共5小题, 44分)
15.(6分) 如图,在△ABC中,AB=AC,点P在BC上.
(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠APC=2∠ABC.求证:PD∥AB.
16.(8分) 如图,在△ABC和△ADE中,==,点B,D,E在一条直线上,求证:△ABD∽△ACE.
17.(8分) 如图所示,三个边长为1个单位长度的正方形ABCD,ABEF,EFGH拼在一起.
(1)请找岀中相似的两个三角形,并证明;
(2)直接写出∠1,∠2,∠3这三个角度数之和.
18.(10分) 如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
(1)求证:GD·AB=DF·BG;
(2)连接CF,求证:∠CFB=45°.
19.(12分) 如图,在 ABCD中,DE⊥AC于点O,交BC于点E,EG=EC,GF∥AD交DE于点F,连接FC,点H为线段AO上一点,连接HD,HF.
(1)判断四边形GECF的形状,并说明理由;
(2)当∠DHF=∠HAD时,求证:AH·CH=EC·AD.
参考答案
1-4BADC 5-8DBAC
9. 10.1.24 m 11. 12. 13.(-5,-1) 14.2
15.解:(1)如图:作出∠APD=∠ABP,即可得到△PCD∽△ABP
(2)如图,∵∠APC=2∠ABC,∠APD=∠ABC,∴∠DPC=∠ABC,∴PD∥AB
16.证明:∵在△ABC和△ADE中, ==,∴△ABC∽△ADE,∴∠BAC=∠DAE,∴∠BAD=∠CAE,∵=,∴=,∴△ABD∽△ACE
17.解:(1)ACF∽ΔAHC.理由如下:∵AC=,AF=1,AH=2,∴==,而∠FAC=∠CAH,∴△ACF∽△AHC
(2)∵△ACF∽△AHC,∴∠2=∠ACH,而∠1=∠ACH+∠3,∴∠1=∠2+∠3.∵∠1=45°,∴∠1+∠2+∠3=90°
18.证明:(1)∵四边形ABCD是正方形∴∠BCD=∠ADC=90°,AB=BC,∵BF⊥DE,∴∠GFD=90°,∴∠BCD=∠GFD,∵∠BGC=∠FGD,∴△BGC∽△DGF,∴=,∴DG·BC=DF·BG,∵AB=BC,∴DG·AB=DF·BG
(2)连接BD,CF,∵△BGC∽△DGF,∴=,∴=,又∵∠BGD=∠CGF,∴△BGD∽△CGF,∴∠BDG=∠CFG,∵四边形ABCD是正方形,BD是对角线,∴∠BDG=∠ADC=45°,∴∠CFB=45°
19. 解:(1)四边形GECF是菱形,∵EG=EC,DE⊥AC,∴GO=CO,∵GF∥AD,AD∥BC,∴GF∥BC,∴∠FGO=∠ECO,∠GFO=∠CEO,∴△GFO≌△CEO(AAS),∴GF=EC,∴四边形GECF是平行四边形,又∵EG=EC,∴平行四边形GECF是菱形
(2)∵∠DHC=∠DAH+∠ADH=∠DHF+∠FHC,∠DHF=∠HAD,∴∠ADH=∠FHC,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAH=∠ACB,∵四边形GECF是菱形,∴EC=CF,∠HCF=∠ACB,∴∠HCF=∠DAH,∴△ADH∽△CHF,∴=,AH·CH=EC·AD
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
