第二章 一元二次方程 单元检测试题 2021-2022学年北师大版九年级数学上册(word版含答案)
文档属性
| 名称 | 第二章 一元二次方程 单元检测试题 2021-2022学年北师大版九年级数学上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 84.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 14:08:04 | ||
图片预览



文档简介
九年级数学上册 第二章 一元二次方程 单元检测试题
班级____________姓名____________考号___________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 关于的方程是一元二次方程,则值为( )
A.或 B. C. D.且
2. 根据表格中的信息,估计一元二次方程 (,,为常数,) 的一个解的范围为( )
A. B. C. D.
3. 一元二次方程配方后可变形为( )
A. B. C. D.
4. 关于的一元二次方程有实数根,则的取值范围是( )
A.且 B. C. D.且
5. 三角形的两边长分别为米和米,第三边的长是方程的一个根,则这个三角形的周长为( )
A. B. C.或 D.
6. 如图,学校课外生物小组的试验园地是长米,宽米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为平方米,则小道的宽为
A.米 B.米 C.米 D.米
7. 随着国内新冠疫情逐渐好转,市场对口罩的需求量越来越少,根据统计,某口罩厂月份出货量仅为月份的,设月份到月份口罩出厂量平均每月的下降率为,则下列关于的方程正确的是( )
A. B.
C. D.
8. 杨倩在东京奥运女子米气步枪决赛中夺得冠军,为中国代表团揽人首枚金牌,随后杨倩同款“小黄鸭”发卡在电商平台上爆单,该款发卡在某电商平台上月日的销量为个,月日和月日的总销量是个.若月日和日较前一天的增长率均为,则可列方程正确的是( )
A.
B.
C.
D.
9. 某班的每一个同学都将“建党百年”纪念卡向全班其他同学各送一张表示留念,全班共送了张相片,如果全班有名学生,根据题意,列出方程为
A. B.
C. D.
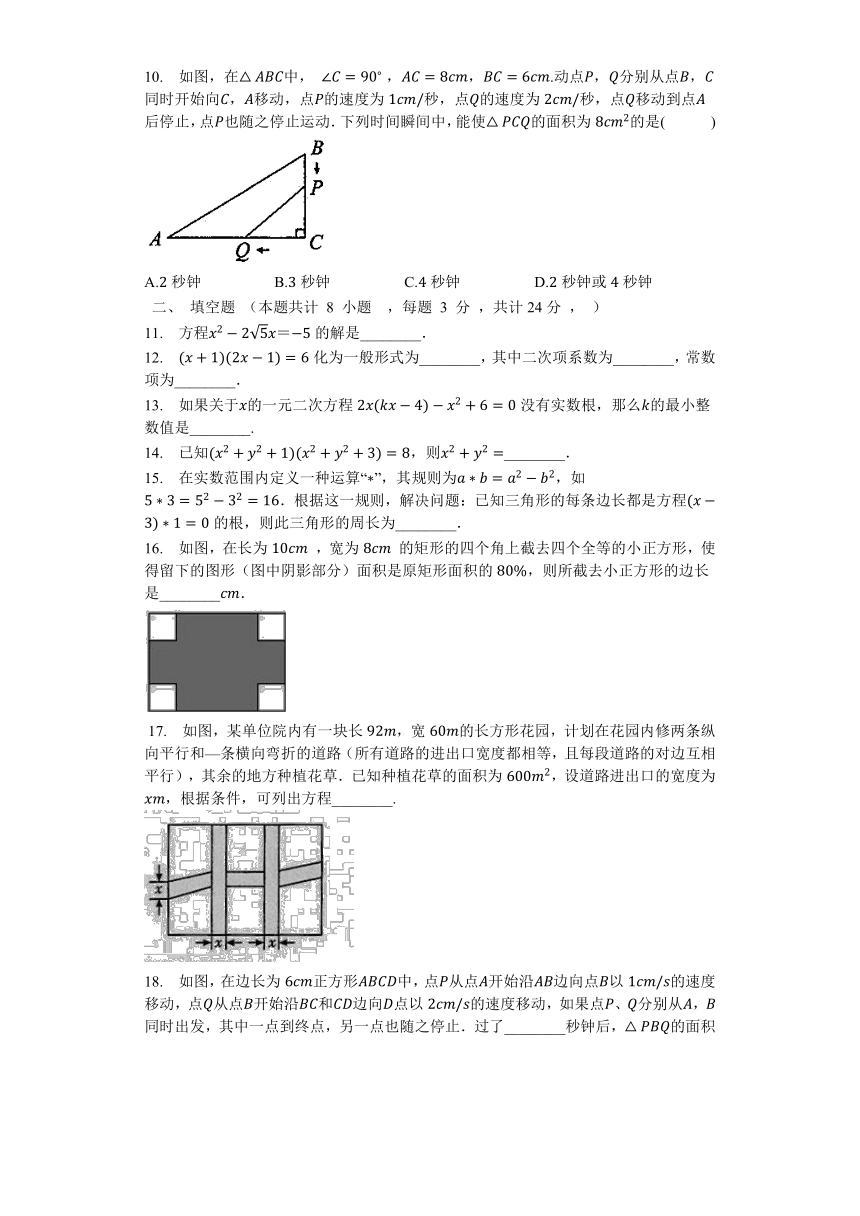
10. 如图,在中, ,,.动点,分别从点,同时开始向,移动,点的速度为秒,点的速度为秒,点移动到点后停止,点也随之停止运动.下列时间瞬间中,能使的面积为的是( )
A.秒钟 B.秒钟 C.秒钟 D.秒钟或秒钟
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
11. 方程=的解是________.
12. 化为一般形式为________,其中二次项系数为________,常数项为________.
13. 如果关于的一元二次方程没有实数根,那么的最小整数值是________.
14. 已知,则________.
15. 在实数范围内定义一种运算“”,其规则为,如.根据这一规则,解决问题:已知三角形的每条边长都是方程的根,则此三角形的周长为________.
16. 如图,在长为 ,宽为 的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的,则所截去小正方形的边长是________.
17. 如图,某单位院内有一块长,宽的长方形花园,计划在花园内修两条纵向平行和—条横向弯折的道路(所有道路的进出口宽度都相等,且每段道路的对边互相平行),其余的地方种植花草.已知种植花草的面积为,设道路进出口的宽度为,根据条件,可列出方程________.
18. 如图,在边长为正方形中,点从点开始沿边向点以的速度移动,点从点开始沿和边向点以的速度移动,如果点、分别从,同时出发,其中一点到终点,另一点也随之停止.过了________秒钟后,的面积等于.
三、 解答题 (本题共计 7 小题 ,共计66分 , )
19.(20分) 解方程.
.
20.(6分) 已知关于的方程有实数根.
(1)求的取值范围;
(2)为何值时,方程有两个相等的实数根?并求出这两个实数根.
21.(8分) 李师傅去年开了一家商店,今年月份开始盈利,月份盈利元,月份的盈利达到元,且从月到月,每月盈利的平均增长率都相同.
求每月盈利的增长率;
按照这个平均增长率,预计月份这家商店的盈利将达到多少元?
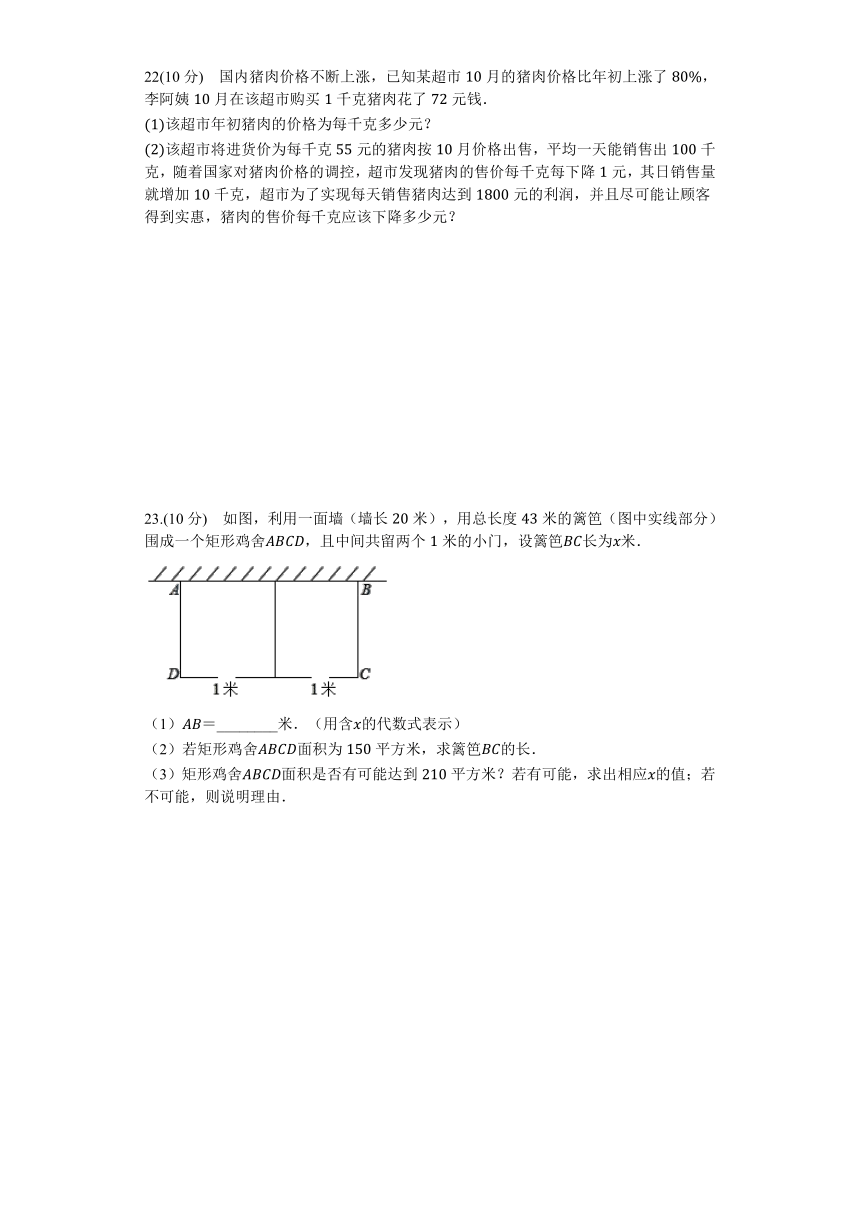
22(10分) 国内猪肉价格不断上涨,已知某超市月的猪肉价格比年初上涨了,李阿姨月在该超市购买千克猪肉花了元钱.
该超市年初猪肉的价格为每千克多少元?
该超市将进货价为每千克元的猪肉按月价格出售,平均一天能销售出千克,随着国家对猪肉价格的调控,超市发现猪肉的售价每千克每下降元,其日销售量就增加千克,超市为了实现每天销售猪肉达到元的利润,并且尽可能让顾客得到实惠,猪肉的售价每千克应该下降多少元?
23.(10分) 如图,利用一面墙(墙长米),用总长度米的篱笆(图中实线部分)围成一个矩形鸡舍,且中间共留两个米的小门,设篱笆长为米.
(1)=________米.(用含的代数式表示)
(2)若矩形鸡舍面积为平方米,求篱笆的长.
(3)矩形鸡舍面积是否有可能达到平方米?若有可能,求出相应的值;若不可能,则说明理由.
24.(12分) 如图,在中,,,.
点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动.如果点,分别从,同时出发,经过几秒,的面积等于?
点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动.如果点,分别从,同时出发,线段能否将分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
若点沿线段方向从点出发以的速度向点移动,点沿射线方向从点出发以的速度移动,,同时出发,问几秒后,的面积为?
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.C
【解析】
利用一元二次方程的定义判断即可.
2.D
【解析】
根据的符号即可估算的一个角的范围.
3.B
【解析】
两边配上一次项系数一半的平方,写成完全平方式即可得.
4.D
【解析】
此题暂无解析
5.A
【解析】
此题暂无解析
6.B
【解析】
设小道的宽为米,则种植区域可看成长为米、宽为米的长方形,根据长方形的面积公式结合种植面积为
平方米,即可得出关于》的一元二次方程,解方程并检验即可得出结论.
7.C
【解析】
根据该口罩厂月份及月份的产量,即可得出关于的一元二次方程,此题得解.
8.D
【解析】
此题暂无解析
9.B
【解析】
如果全班有名学生,那么每名学生应该送的相片为张,根据“全班共送了张相片”,可得出方程为.
10.D
【解析】
设后,满足题意,得出,,,根据面积公式得出方程,即可解答.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.=
【解析】
方程利用配方法求出解即可.
12.,,
【解析】
一元二次方程的一般式:(,,,为常数).叫二次项,叫二次项系数;叫一次项,叫一次项系数;叫常数项.把方程先去括号,再移项,最后合并即可.
13.
【解析】
先把方程变形为关于的一元二次方程的一般形式:,要方程无实数根,则且
,解不等式,并求出满足条件的最小整数.
14.
【解析】
设,已知等式化为关于的方程,求出方程的解得到的值,即可确定出的值.
15.或或
【解析】
利用已知得出,为,进而得出的值,进而得出三角形的周长.
16.
【解析】
等量关系为:矩形面积-四个全等的小正方形面积矩形面积,列方程即可求解.
17.
【解析】
设小道的进出口宽度为米,然后利用其种植花草的面积为平方米列出方程求解即可.
18.或
【解析】
设经过秒,的面积等于,分类讨论当秒时,点在上运动,在上运动,求出面积的表达式,求出一个值,当秒时,点在上运动,在上运动,根据条件列出一个一元一次方程,求出一个值.
三、 解答题 (本题共计 7 小题 ,共计66分 )
19.解:,
,
∴ ,
两边开平方,得:,
∴ ,;
左边因式分解,
得:,
即,
∴ ,
∴ 或,
解得:,;
两边直接开平方,
得:,即,
∴ ,;
原方程整理可得:,
∵ ,,
,
∴ ,
则,
即,.
【解析】
(1)配方法求解可得;
(2)因式分解法求解可得;
(3)直接开平方可得;
(4)先化成一元二次方程的一般式,再利用公式法求解可得.
20.解:(1)关于的方程有实数根,分两种情况讨论:
①即时,是一元一次方程,此时方程即为,必有实数根;
②时,是一元二次方程,
,
解得:且;
综上可知,当时,方程有实数根;
(2)∵ 关于的方程有两个相等的实数根,
∴ ,
解得:,
∴ 方程变为:,
两边同时乘以得:,
解得.
【解析】
(1)根据方程有实数根,分两种情况讨论:时,方程即为,必有实数根;时,,解不等式即可;
(2)根据方程有两个相等的实数根,可得,解方程可得的值,再把的值代入方程,解一元二次方程即可.
21.解:设每月盈利的平均增长率为,根据题意得:
,
解得:,(舍去).
答:每月盈利的平均增长率为.
(元).
答:月份这家商店的盈利达到元.
【解析】
(1)设该商店的月平均增长率为,根据等量关系:月份盈利额(增长率)=月份的盈利额列出方程求解即可.
(2)月份盈利=月份盈利增长率.
22解:设今年年初猪肉的价格为每千克元,
依题意,得,
解得.
答:今年年初猪肉的价格为每千克元.
设猪肉的售价应该下降元,则每日可售出千克,
依题意,得,
整理,得,
解得,.
∵ 让顾客得到实惠,
∴ .
答:猪肉的售价应该下降元.
【解析】
(1)设今年年初猪肉的价格为每千克元,根据“年初价格(增长的百分比)=月份的单价”列方程求解可得;
(2)设猪肉的售价应该下降元,则每日可售出千克,根据“每千克利润销售量=总利润”列方程,解之求得的值,继而结合题意取舍即可得.
23.
依题意,得:=,
整理,得:=,
解得:=,=.
当=时,==,舍去;
当=时,==.
答:篱笆的长为米.
不可能,理由如下:
依题意,得:=,
整理得:=,
∵ ==,
∴ 方程没有实数根,
∴ 矩形鸡舍面积不可能达到平方米.
【解析】
此题暂无解析
24.解:设经过秒,使的面积等于,依题意有
,
解得,,
经检验,,均符合题意.
故经过秒或秒,的面积等于.
不能,理由如下:
设经过秒,线段能否将分成面积相等的两部分,依题意有:
的面积,
,
,
∵ ,
∴ 此方程无实数根,
∴ 线段不能将分成面积相等的两部分;
①点在线段上,点在线段上,
设经过秒,依题意有,
,
,
解得,,
经检验,不符合题意,舍去,
∴ ;
②点在线段上,点在线段延长线上,
设经过秒,依题意有,
,
,
解得,
经检验,符合题意.
综上所述,经过秒或秒后,的面积为.
【解析】
(1)设经过秒,使的面积等于,根据等量关系:的面积等于,列出方程求解即可;
(2)设经过秒,线段能否将分成面积相等的两部分,根据面积之间的等量关系和判别式即可求解;
(3)分三种情况:①点在线段上,点在线段上;②点在线段上,点在线段上;③点在射线上,点在射线上;进行讨论即可求解.
班级____________姓名____________考号___________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 关于的方程是一元二次方程,则值为( )
A.或 B. C. D.且
2. 根据表格中的信息,估计一元二次方程 (,,为常数,) 的一个解的范围为( )
A. B. C. D.
3. 一元二次方程配方后可变形为( )
A. B. C. D.
4. 关于的一元二次方程有实数根,则的取值范围是( )
A.且 B. C. D.且
5. 三角形的两边长分别为米和米,第三边的长是方程的一个根,则这个三角形的周长为( )
A. B. C.或 D.
6. 如图,学校课外生物小组的试验园地是长米,宽米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为平方米,则小道的宽为
A.米 B.米 C.米 D.米
7. 随着国内新冠疫情逐渐好转,市场对口罩的需求量越来越少,根据统计,某口罩厂月份出货量仅为月份的,设月份到月份口罩出厂量平均每月的下降率为,则下列关于的方程正确的是( )
A. B.
C. D.
8. 杨倩在东京奥运女子米气步枪决赛中夺得冠军,为中国代表团揽人首枚金牌,随后杨倩同款“小黄鸭”发卡在电商平台上爆单,该款发卡在某电商平台上月日的销量为个,月日和月日的总销量是个.若月日和日较前一天的增长率均为,则可列方程正确的是( )
A.
B.
C.
D.
9. 某班的每一个同学都将“建党百年”纪念卡向全班其他同学各送一张表示留念,全班共送了张相片,如果全班有名学生,根据题意,列出方程为
A. B.
C. D.
10. 如图,在中, ,,.动点,分别从点,同时开始向,移动,点的速度为秒,点的速度为秒,点移动到点后停止,点也随之停止运动.下列时间瞬间中,能使的面积为的是( )
A.秒钟 B.秒钟 C.秒钟 D.秒钟或秒钟
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
11. 方程=的解是________.
12. 化为一般形式为________,其中二次项系数为________,常数项为________.
13. 如果关于的一元二次方程没有实数根,那么的最小整数值是________.
14. 已知,则________.
15. 在实数范围内定义一种运算“”,其规则为,如.根据这一规则,解决问题:已知三角形的每条边长都是方程的根,则此三角形的周长为________.
16. 如图,在长为 ,宽为 的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的,则所截去小正方形的边长是________.
17. 如图,某单位院内有一块长,宽的长方形花园,计划在花园内修两条纵向平行和—条横向弯折的道路(所有道路的进出口宽度都相等,且每段道路的对边互相平行),其余的地方种植花草.已知种植花草的面积为,设道路进出口的宽度为,根据条件,可列出方程________.
18. 如图,在边长为正方形中,点从点开始沿边向点以的速度移动,点从点开始沿和边向点以的速度移动,如果点、分别从,同时出发,其中一点到终点,另一点也随之停止.过了________秒钟后,的面积等于.
三、 解答题 (本题共计 7 小题 ,共计66分 , )
19.(20分) 解方程.
.
20.(6分) 已知关于的方程有实数根.
(1)求的取值范围;
(2)为何值时,方程有两个相等的实数根?并求出这两个实数根.
21.(8分) 李师傅去年开了一家商店,今年月份开始盈利,月份盈利元,月份的盈利达到元,且从月到月,每月盈利的平均增长率都相同.
求每月盈利的增长率;
按照这个平均增长率,预计月份这家商店的盈利将达到多少元?
22(10分) 国内猪肉价格不断上涨,已知某超市月的猪肉价格比年初上涨了,李阿姨月在该超市购买千克猪肉花了元钱.
该超市年初猪肉的价格为每千克多少元?
该超市将进货价为每千克元的猪肉按月价格出售,平均一天能销售出千克,随着国家对猪肉价格的调控,超市发现猪肉的售价每千克每下降元,其日销售量就增加千克,超市为了实现每天销售猪肉达到元的利润,并且尽可能让顾客得到实惠,猪肉的售价每千克应该下降多少元?
23.(10分) 如图,利用一面墙(墙长米),用总长度米的篱笆(图中实线部分)围成一个矩形鸡舍,且中间共留两个米的小门,设篱笆长为米.
(1)=________米.(用含的代数式表示)
(2)若矩形鸡舍面积为平方米,求篱笆的长.
(3)矩形鸡舍面积是否有可能达到平方米?若有可能,求出相应的值;若不可能,则说明理由.
24.(12分) 如图,在中,,,.
点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动.如果点,分别从,同时出发,经过几秒,的面积等于?
点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动.如果点,分别从,同时出发,线段能否将分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
若点沿线段方向从点出发以的速度向点移动,点沿射线方向从点出发以的速度移动,,同时出发,问几秒后,的面积为?
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.C
【解析】
利用一元二次方程的定义判断即可.
2.D
【解析】
根据的符号即可估算的一个角的范围.
3.B
【解析】
两边配上一次项系数一半的平方,写成完全平方式即可得.
4.D
【解析】
此题暂无解析
5.A
【解析】
此题暂无解析
6.B
【解析】
设小道的宽为米,则种植区域可看成长为米、宽为米的长方形,根据长方形的面积公式结合种植面积为
平方米,即可得出关于》的一元二次方程,解方程并检验即可得出结论.
7.C
【解析】
根据该口罩厂月份及月份的产量,即可得出关于的一元二次方程,此题得解.
8.D
【解析】
此题暂无解析
9.B
【解析】
如果全班有名学生,那么每名学生应该送的相片为张,根据“全班共送了张相片”,可得出方程为.
10.D
【解析】
设后,满足题意,得出,,,根据面积公式得出方程,即可解答.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.=
【解析】
方程利用配方法求出解即可.
12.,,
【解析】
一元二次方程的一般式:(,,,为常数).叫二次项,叫二次项系数;叫一次项,叫一次项系数;叫常数项.把方程先去括号,再移项,最后合并即可.
13.
【解析】
先把方程变形为关于的一元二次方程的一般形式:,要方程无实数根,则且
,解不等式,并求出满足条件的最小整数.
14.
【解析】
设,已知等式化为关于的方程,求出方程的解得到的值,即可确定出的值.
15.或或
【解析】
利用已知得出,为,进而得出的值,进而得出三角形的周长.
16.
【解析】
等量关系为:矩形面积-四个全等的小正方形面积矩形面积,列方程即可求解.
17.
【解析】
设小道的进出口宽度为米,然后利用其种植花草的面积为平方米列出方程求解即可.
18.或
【解析】
设经过秒,的面积等于,分类讨论当秒时,点在上运动,在上运动,求出面积的表达式,求出一个值,当秒时,点在上运动,在上运动,根据条件列出一个一元一次方程,求出一个值.
三、 解答题 (本题共计 7 小题 ,共计66分 )
19.解:,
,
∴ ,
两边开平方,得:,
∴ ,;
左边因式分解,
得:,
即,
∴ ,
∴ 或,
解得:,;
两边直接开平方,
得:,即,
∴ ,;
原方程整理可得:,
∵ ,,
,
∴ ,
则,
即,.
【解析】
(1)配方法求解可得;
(2)因式分解法求解可得;
(3)直接开平方可得;
(4)先化成一元二次方程的一般式,再利用公式法求解可得.
20.解:(1)关于的方程有实数根,分两种情况讨论:
①即时,是一元一次方程,此时方程即为,必有实数根;
②时,是一元二次方程,
,
解得:且;
综上可知,当时,方程有实数根;
(2)∵ 关于的方程有两个相等的实数根,
∴ ,
解得:,
∴ 方程变为:,
两边同时乘以得:,
解得.
【解析】
(1)根据方程有实数根,分两种情况讨论:时,方程即为,必有实数根;时,,解不等式即可;
(2)根据方程有两个相等的实数根,可得,解方程可得的值,再把的值代入方程,解一元二次方程即可.
21.解:设每月盈利的平均增长率为,根据题意得:
,
解得:,(舍去).
答:每月盈利的平均增长率为.
(元).
答:月份这家商店的盈利达到元.
【解析】
(1)设该商店的月平均增长率为,根据等量关系:月份盈利额(增长率)=月份的盈利额列出方程求解即可.
(2)月份盈利=月份盈利增长率.
22解:设今年年初猪肉的价格为每千克元,
依题意,得,
解得.
答:今年年初猪肉的价格为每千克元.
设猪肉的售价应该下降元,则每日可售出千克,
依题意,得,
整理,得,
解得,.
∵ 让顾客得到实惠,
∴ .
答:猪肉的售价应该下降元.
【解析】
(1)设今年年初猪肉的价格为每千克元,根据“年初价格(增长的百分比)=月份的单价”列方程求解可得;
(2)设猪肉的售价应该下降元,则每日可售出千克,根据“每千克利润销售量=总利润”列方程,解之求得的值,继而结合题意取舍即可得.
23.
依题意,得:=,
整理,得:=,
解得:=,=.
当=时,==,舍去;
当=时,==.
答:篱笆的长为米.
不可能,理由如下:
依题意,得:=,
整理得:=,
∵ ==,
∴ 方程没有实数根,
∴ 矩形鸡舍面积不可能达到平方米.
【解析】
此题暂无解析
24.解:设经过秒,使的面积等于,依题意有
,
解得,,
经检验,,均符合题意.
故经过秒或秒,的面积等于.
不能,理由如下:
设经过秒,线段能否将分成面积相等的两部分,依题意有:
的面积,
,
,
∵ ,
∴ 此方程无实数根,
∴ 线段不能将分成面积相等的两部分;
①点在线段上,点在线段上,
设经过秒,依题意有,
,
,
解得,,
经检验,不符合题意,舍去,
∴ ;
②点在线段上,点在线段延长线上,
设经过秒,依题意有,
,
,
解得,
经检验,符合题意.
综上所述,经过秒或秒后,的面积为.
【解析】
(1)设经过秒,使的面积等于,根据等量关系:的面积等于,列出方程求解即可;
(2)设经过秒,线段能否将分成面积相等的两部分,根据面积之间的等量关系和判别式即可求解;
(3)分三种情况:①点在线段上,点在线段上;②点在线段上,点在线段上;③点在射线上,点在射线上;进行讨论即可求解.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
