2021-2022学年冀教新版九年级上册数学第25章 图形的相似单元测试卷(word版、含解析)
文档属性
| 名称 | 2021-2022学年冀教新版九年级上册数学第25章 图形的相似单元测试卷(word版、含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 00:00:00 | ||
图片预览


文档简介
2021-2022学年冀教新版九年级上册数学《第25章 图形的相似》单元测试卷
一.选择题
1.已知=,那么下列式子中一定成立的是( )
A.4m=3n B.3m=4n C.m=4n D.mn=12
2.若a:b=3:4,且a+b=14,则2a﹣b的值是( )
A.4 B.2 C.20 D.14
3.在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,则甲、乙两地间的实际距离是( )
A.1250km B.125km C.12.5km D.1.25km
4.点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A.6cm B.(5+1)cm C.5(﹣1)cm D.(5﹣1)cm
5.如图,直线a∥b∥c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3,则EF的长是( )
A.5 B.6 C.7 D.8
6.已知≠0,则的值为( )
A. B.﹣ C.2 D.
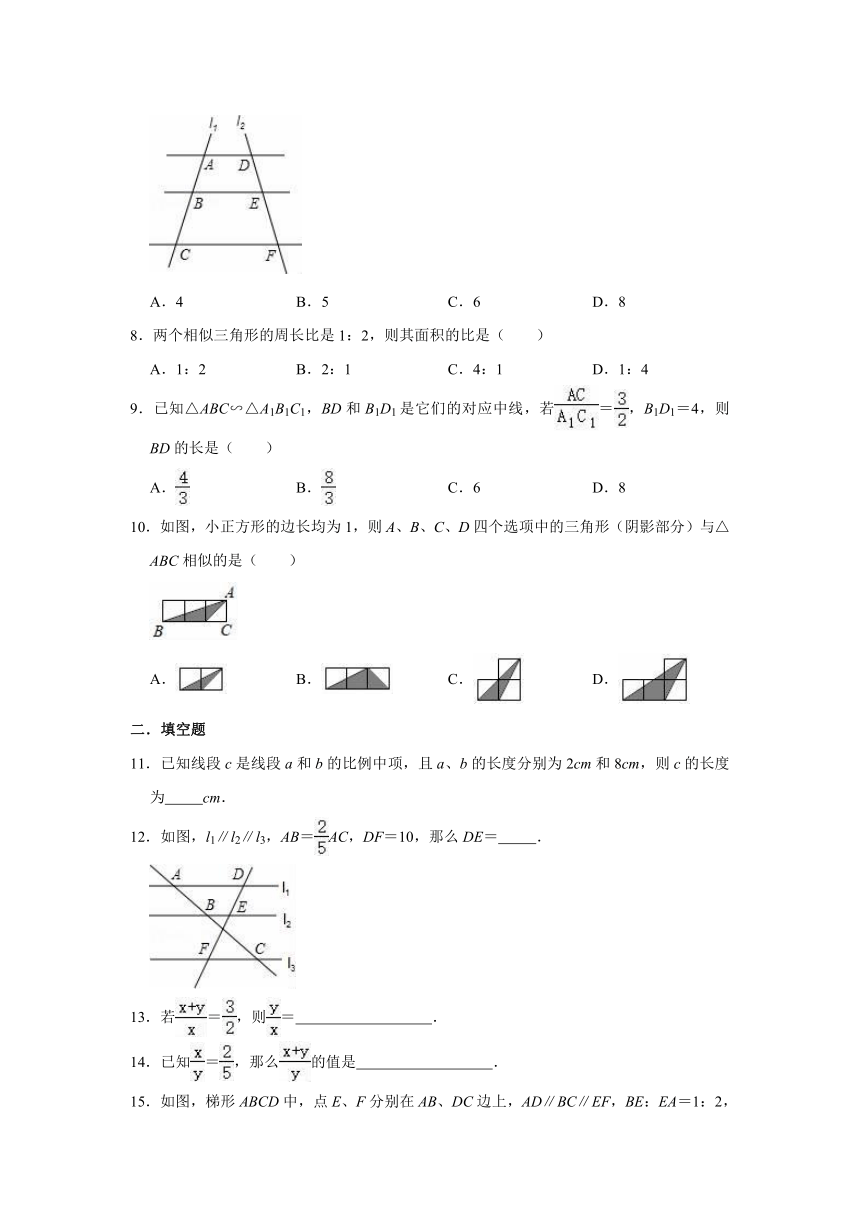
7.如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )
A.4 B.5 C.6 D.8
8.两个相似三角形的周长比是1:2,则其面积的比是( )
A.1:2 B.2:1 C.4:1 D.1:4
9.已知△ABC∽△A1B1C1,BD和B1D1是它们的对应中线,若=,B1D1=4,则BD的长是( )
A. B. C.6 D.8
10.如图,小正方形的边长均为1,则A、B、C、D四个选项中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
二.填空题
11.已知线段c是线段a和b的比例中项,且a、b的长度分别为2cm和8cm,则c的长度为 cm.
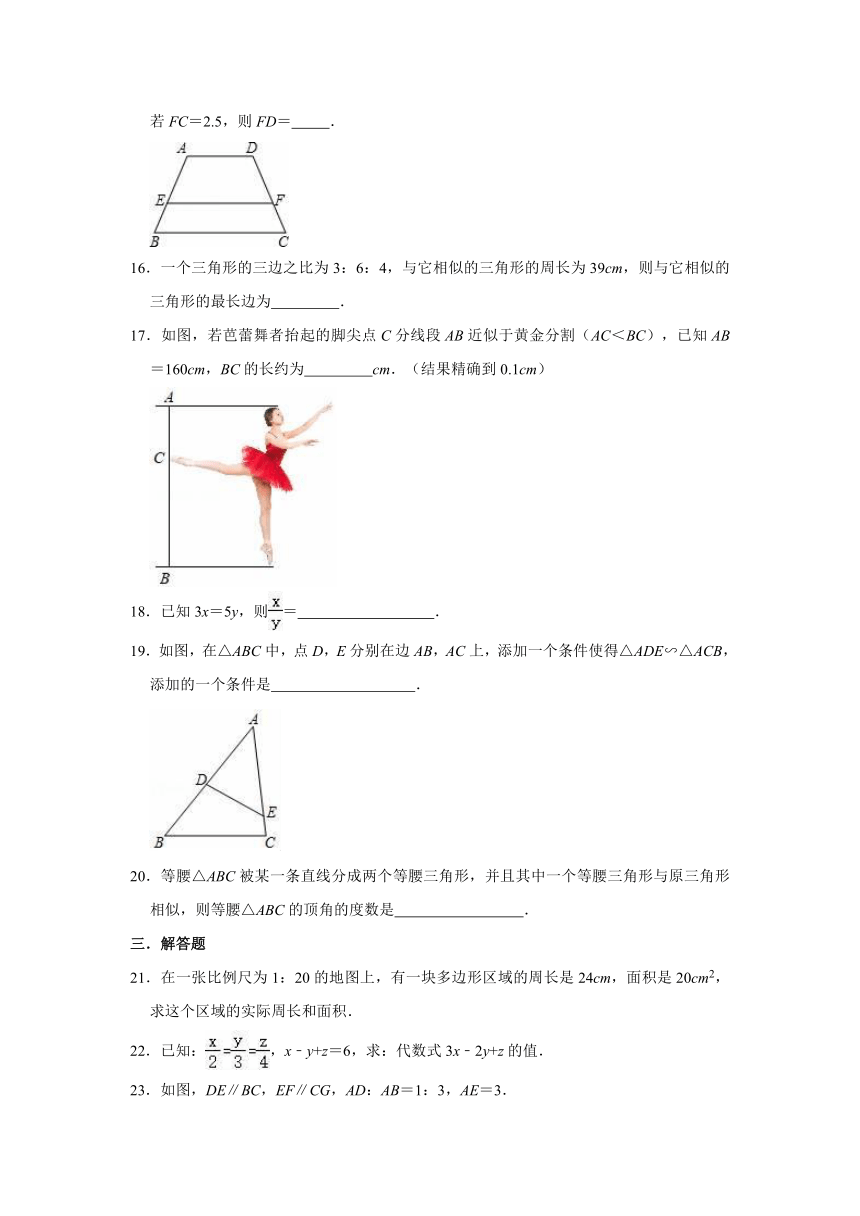
12.如图,l1∥l2∥l3,AB=AC,DF=10,那么DE= .
13.若=,则= .
14.已知=,那么的值是 .
15.如图,梯形ABCD中,点E、F分别在AB、DC边上,AD∥BC∥EF,BE:EA=1:2,若FC=2.5,则FD= .
16.一个三角形的三边之比为3:6:4,与它相似的三角形的周长为39cm,则与它相似的三角形的最长边为 .
17.如图,若芭蕾舞者抬起的脚尖点C分线段AB近似于黄金分割(AC<BC),已知AB=160cm,BC的长约为 cm.(结果精确到0.1cm)
18.已知3x=5y,则= .
19.如图,在△ABC中,点D,E分别在边AB,AC上,添加一个条件使得△ADE∽△ACB,添加的一个条件是 .
20.等腰△ABC被某一条直线分成两个等腰三角形,并且其中一个等腰三角形与原三角形相似,则等腰△ABC的顶角的度数是 .
三.解答题
21.在一张比例尺为1:20的地图上,有一块多边形区域的周长是24cm,面积是20cm2,求这个区域的实际周长和面积.
22.已知:,x﹣y+z=6,求:代数式3x﹣2y+z的值.
23.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD AG=AF AB.
24.已知a、b、c是△ABC的三边,且满足==,且a+b+c=12,请你探索△ABC的形状.
25.已知△ABC和△DEF中,有,且△DEF和△ABC的周长之差为15厘米,求△ABC和△DEF的周长.
26.若一个矩形的短边与长边的比值为(黄金分割数),我们把这样的矩形叫做黄金矩形.
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由;
(3)归纳:通过上述操作及探究,请概括出具有一般性的结论(不需要证明).
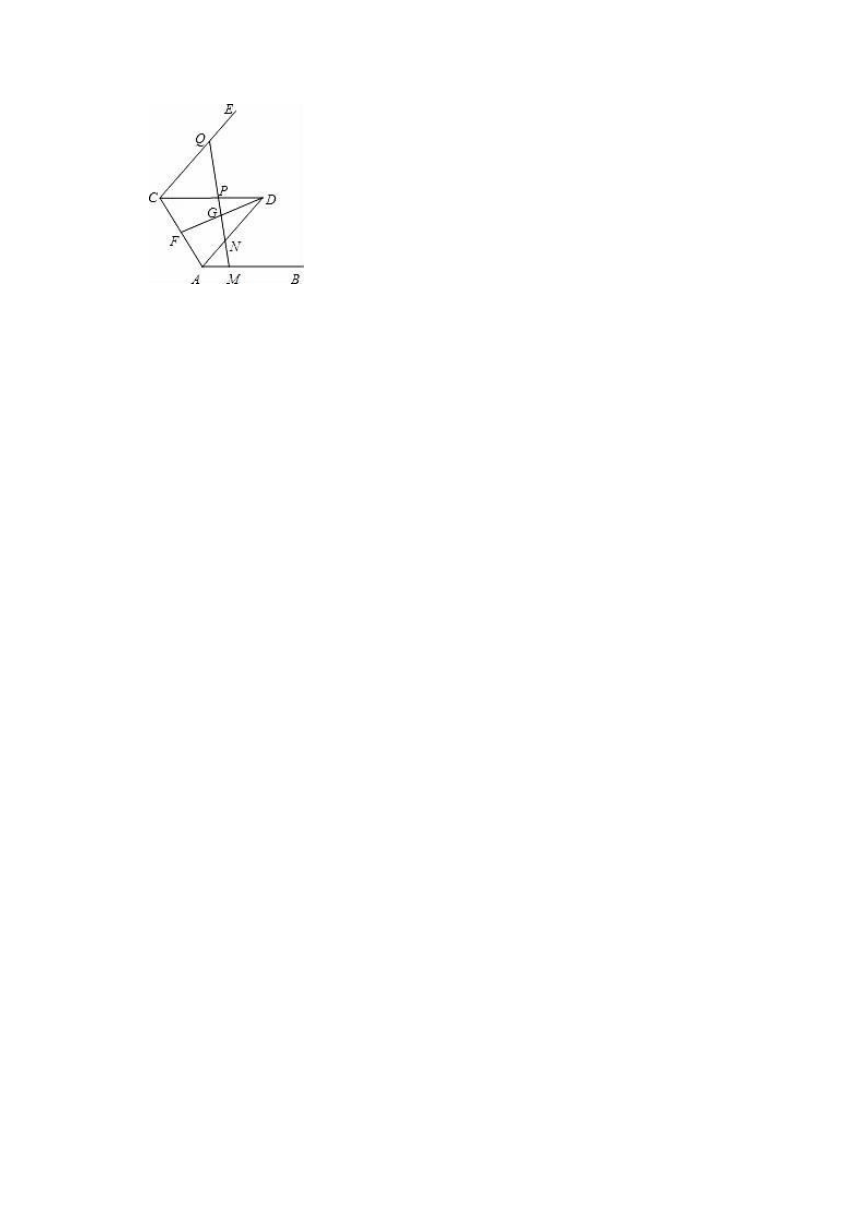
27.如图,AB∥CD、AD∥CE,F、G分别是AC和FD的中点,过G的直线依次交AB、AD、CD、CE于点M、N、P、Q,
求证:MN+PQ=2PN.
参考答案与试题解析
一.选择题
1.解:由=,得4m=3n.
A、4m=3n,故A正确;
B、4m=3n,故B错误;
C、m=,故C错误;
D、4m=3n,故D错误;
故选:A.
2.解:由a:b=3:4知3b=4a,
所以b=.
所以由a+b=14得到:a+=14,
解得a=6.
所以b=8.
所以2a﹣b=2×6﹣8=4.
故选:A.
3.解:设甲、乙两地间的实际距离为x,则:
=,
解得x=125000cm=1.25km.
故选:D.
4.解:∵点C是线段AB的黄金分割点(AC>BC),
∴AC=AB,
而AB=10cm,
∴AC=×10=5(﹣1)cm.
故选:C.
5.解:∵直线a∥b∥c,
∴=,即=,
∴EF=6.
故选:B.
6.解:由≠0,得
b=,c=2a,
==﹣.
故选:B.
7.解:∵AD∥BE∥CF,
∴=,
∴=,
∴EF=6,
∴DF=EF+DE=8,
故选:D.
8.解:∵两个相似三角形的周长比是1:2,
∴两个相似三角形的相似比为1:2,
∴其面积的比是1:4,
故选:D.
9.解:∵△ABC∽△A1B1C1,
∴,
∴,
∴BD=6,
故选:C.
10.解:已知给出的三角形的各边分别为、2、、
只有选项A的各边为1、、与它的各边对应成比例.
故选:A.
二.填空题
11.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
所以c2=2×8,解得c=±4(线段是正数,负值舍去),
故答案为:4.
12.解:∵l1∥l2∥l3,
∴.
∵AB=AC,
∴,
∴.
∵DF=10,
∴,
∴DE=4.
故答案为:4.
13.解:∵=,
∴2x+2y=3x,
故2y=x,
则=.
故答案为:.
14.解:∵=,
∴设x=2a,则y=5a,
那么==.
故答案为:.
15.解:∵AD∥BC∥EF,BE:EA=1:2,
∴FC:FD=1:2,
∵FC=2.5,
∴FD=5.
故答案为5.
16.解:∵一个三角形的三边之比为3:6:4,
∴与它相似的三角形的三边之比为3:6:4,
∵与它相似的三角形的周长为39cm,
∴与它相似的三角形的最长边为:39×=18(cm).
故答案为:18cm.
17.解:∵点C为线段AB的黄金分割点(AC<BC),AB=160cm,
∴BC=AB=×160≈98.9,
故答案为:98.9.
18.解:∵3x=5y,
∴=,
故答案为:.
19.解:添加条件为∠AED=∠B,理由如下:
∵∠A=∠A,∠AED=∠B,
∴△ADE∽△ACB;
故答案为:∠AED=∠B(答案不唯一).
20.解:分以下三种情况:
(1)如图,△ABC中,AB=AC,BD=AD,AC=CD,△ABD∽△BCA,求∠BAC的度数.
∵AB=AC,BD=AD,AC=CD,
∴∠B=∠C=∠BAD,∠CDA=∠CAD,
∵∠CDA=2∠B,
∴∠CAB=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BAC=108°;
(2)如图,△ABC中,AB=AC,AD=BD=CD,△ABD∽△BCA,求∠BAC的度数.
∵AB=AC,AD=BD=CD,
∴∠B=∠C=∠DAC=∠DAB,
∴∠BAC=2∠B,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠B=45°,
∴∠BAC=90°;
(3)如图,△ABC中,AB=AC,BD=AD=BC,△BCD∽△ABC,求∠BAC的度数.
∵AB=AC,BD=AD=BC,
∴∠ABC=∠C,∠A=∠ABD,∠BDC=∠C,
∵∠BDC=2∠A,
∴∠C=2∠A=∠ABC,
∵∠A+∠ABC+∠C=180°,
∴5∠A=180°,
∴∠A=36°;
综上所述,等腰△ABC的顶角的度数是36°或90°或108°,
故答案为:36°或90°或108°.
三.解答题
21.解:地图与该地区的实际图形相似,相似比就是比例尺为1:20,周长的比就是相似比,设实际周长是xcm,则
24:x=1:20,
解得:x=480,
面积的比等于相似比的平方,设实际面积是ycm2,则
20:y=(1:20)2,
解得y=8000,
答:这个区域的实际周长480cm,面积8000cm2.
22.解:设=k,
可得:x=2k,y=3k,z=4k,
把x=2k,y=3k,z=4k代入x﹣y+z=6,
可得:2k﹣3k+4k=6,
解得:k=2,
所以x=4,y=6,z=8,
把x=4,y=6,z=8代入3x﹣2y+z=12﹣12+8=8.
23.(1)解:
∵DE∥BC,
∴=,
又=,AE=3,
∴=,
解得AC=9,
∴EC=AC﹣AE=9﹣3=6;
(2)证明:
∵DE∥BC,EF∥CG,
∴==,
∴AD AG=AF AB.
24.解:设===k,
可得a=3k﹣4,b=2k﹣3,c=4k﹣8,
代入a+b+c=12得:9k﹣15=12,
解得:k=3,
∴a=5,b=3,c=4,
则△ABC为直角三角形.
25.解:设△ABC和△DEF的周长分别是x厘米和y厘米.
∵,
∴==①
由题意可得:y﹣x=15 ②
由①式得x=y③
将③式代入②式得:y﹣y=15,
∴y=45,
将y=45代入③式得:x=30,
答:△ABC和△DEF的周长分别是30厘米和45厘米.
26.解:(1)如图.
(2)探究:四边形EBCF是矩形,而且是黄金矩形.
∵四边形AEFD是正方形,
∴∠AEF=90°
∴∠BEF=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°
∴∠BEF=∠B=∠C=90°,
∴四边形EBCF是矩形.
【方法1】设
∴
∴矩形EBCF是黄金矩形.
【方法2】设,
∴
∴矩形EBCF是黄金矩形.
(3)归纳:在黄金矩形内以短边为边作一个正方形后,所得到的另外一个四边形是矩形,而且是黄金矩形.
27.证明:延长BA、EC,设交点为O,则四边形OADC为平行四边形,
∵F是AC的中点,
∴DF的延长线必过O点,且.
∵AB∥CD,
∴.
∵AD∥CE,
∴.
∴==.
又∵=,
∴OQ=3DN.
∴CQ=OQ﹣OC=3DN﹣OC=3DN﹣AD,AN=AD﹣DN.
∴AN+CQ=2DN.
∴==2.
即MN+PQ=2PN.
一.选择题
1.已知=,那么下列式子中一定成立的是( )
A.4m=3n B.3m=4n C.m=4n D.mn=12
2.若a:b=3:4,且a+b=14,则2a﹣b的值是( )
A.4 B.2 C.20 D.14
3.在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,则甲、乙两地间的实际距离是( )
A.1250km B.125km C.12.5km D.1.25km
4.点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A.6cm B.(5+1)cm C.5(﹣1)cm D.(5﹣1)cm
5.如图,直线a∥b∥c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3,则EF的长是( )
A.5 B.6 C.7 D.8
6.已知≠0,则的值为( )
A. B.﹣ C.2 D.
7.如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )
A.4 B.5 C.6 D.8
8.两个相似三角形的周长比是1:2,则其面积的比是( )
A.1:2 B.2:1 C.4:1 D.1:4
9.已知△ABC∽△A1B1C1,BD和B1D1是它们的对应中线,若=,B1D1=4,则BD的长是( )
A. B. C.6 D.8
10.如图,小正方形的边长均为1,则A、B、C、D四个选项中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
二.填空题
11.已知线段c是线段a和b的比例中项,且a、b的长度分别为2cm和8cm,则c的长度为 cm.
12.如图,l1∥l2∥l3,AB=AC,DF=10,那么DE= .
13.若=,则= .
14.已知=,那么的值是 .
15.如图,梯形ABCD中,点E、F分别在AB、DC边上,AD∥BC∥EF,BE:EA=1:2,若FC=2.5,则FD= .
16.一个三角形的三边之比为3:6:4,与它相似的三角形的周长为39cm,则与它相似的三角形的最长边为 .
17.如图,若芭蕾舞者抬起的脚尖点C分线段AB近似于黄金分割(AC<BC),已知AB=160cm,BC的长约为 cm.(结果精确到0.1cm)
18.已知3x=5y,则= .
19.如图,在△ABC中,点D,E分别在边AB,AC上,添加一个条件使得△ADE∽△ACB,添加的一个条件是 .
20.等腰△ABC被某一条直线分成两个等腰三角形,并且其中一个等腰三角形与原三角形相似,则等腰△ABC的顶角的度数是 .
三.解答题
21.在一张比例尺为1:20的地图上,有一块多边形区域的周长是24cm,面积是20cm2,求这个区域的实际周长和面积.
22.已知:,x﹣y+z=6,求:代数式3x﹣2y+z的值.
23.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD AG=AF AB.
24.已知a、b、c是△ABC的三边,且满足==,且a+b+c=12,请你探索△ABC的形状.
25.已知△ABC和△DEF中,有,且△DEF和△ABC的周长之差为15厘米,求△ABC和△DEF的周长.
26.若一个矩形的短边与长边的比值为(黄金分割数),我们把这样的矩形叫做黄金矩形.
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由;
(3)归纳:通过上述操作及探究,请概括出具有一般性的结论(不需要证明).
27.如图,AB∥CD、AD∥CE,F、G分别是AC和FD的中点,过G的直线依次交AB、AD、CD、CE于点M、N、P、Q,
求证:MN+PQ=2PN.
参考答案与试题解析
一.选择题
1.解:由=,得4m=3n.
A、4m=3n,故A正确;
B、4m=3n,故B错误;
C、m=,故C错误;
D、4m=3n,故D错误;
故选:A.
2.解:由a:b=3:4知3b=4a,
所以b=.
所以由a+b=14得到:a+=14,
解得a=6.
所以b=8.
所以2a﹣b=2×6﹣8=4.
故选:A.
3.解:设甲、乙两地间的实际距离为x,则:
=,
解得x=125000cm=1.25km.
故选:D.
4.解:∵点C是线段AB的黄金分割点(AC>BC),
∴AC=AB,
而AB=10cm,
∴AC=×10=5(﹣1)cm.
故选:C.
5.解:∵直线a∥b∥c,
∴=,即=,
∴EF=6.
故选:B.
6.解:由≠0,得
b=,c=2a,
==﹣.
故选:B.
7.解:∵AD∥BE∥CF,
∴=,
∴=,
∴EF=6,
∴DF=EF+DE=8,
故选:D.
8.解:∵两个相似三角形的周长比是1:2,
∴两个相似三角形的相似比为1:2,
∴其面积的比是1:4,
故选:D.
9.解:∵△ABC∽△A1B1C1,
∴,
∴,
∴BD=6,
故选:C.
10.解:已知给出的三角形的各边分别为、2、、
只有选项A的各边为1、、与它的各边对应成比例.
故选:A.
二.填空题
11.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
所以c2=2×8,解得c=±4(线段是正数,负值舍去),
故答案为:4.
12.解:∵l1∥l2∥l3,
∴.
∵AB=AC,
∴,
∴.
∵DF=10,
∴,
∴DE=4.
故答案为:4.
13.解:∵=,
∴2x+2y=3x,
故2y=x,
则=.
故答案为:.
14.解:∵=,
∴设x=2a,则y=5a,
那么==.
故答案为:.
15.解:∵AD∥BC∥EF,BE:EA=1:2,
∴FC:FD=1:2,
∵FC=2.5,
∴FD=5.
故答案为5.
16.解:∵一个三角形的三边之比为3:6:4,
∴与它相似的三角形的三边之比为3:6:4,
∵与它相似的三角形的周长为39cm,
∴与它相似的三角形的最长边为:39×=18(cm).
故答案为:18cm.
17.解:∵点C为线段AB的黄金分割点(AC<BC),AB=160cm,
∴BC=AB=×160≈98.9,
故答案为:98.9.
18.解:∵3x=5y,
∴=,
故答案为:.
19.解:添加条件为∠AED=∠B,理由如下:
∵∠A=∠A,∠AED=∠B,
∴△ADE∽△ACB;
故答案为:∠AED=∠B(答案不唯一).
20.解:分以下三种情况:
(1)如图,△ABC中,AB=AC,BD=AD,AC=CD,△ABD∽△BCA,求∠BAC的度数.
∵AB=AC,BD=AD,AC=CD,
∴∠B=∠C=∠BAD,∠CDA=∠CAD,
∵∠CDA=2∠B,
∴∠CAB=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BAC=108°;
(2)如图,△ABC中,AB=AC,AD=BD=CD,△ABD∽△BCA,求∠BAC的度数.
∵AB=AC,AD=BD=CD,
∴∠B=∠C=∠DAC=∠DAB,
∴∠BAC=2∠B,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠B=45°,
∴∠BAC=90°;
(3)如图,△ABC中,AB=AC,BD=AD=BC,△BCD∽△ABC,求∠BAC的度数.
∵AB=AC,BD=AD=BC,
∴∠ABC=∠C,∠A=∠ABD,∠BDC=∠C,
∵∠BDC=2∠A,
∴∠C=2∠A=∠ABC,
∵∠A+∠ABC+∠C=180°,
∴5∠A=180°,
∴∠A=36°;
综上所述,等腰△ABC的顶角的度数是36°或90°或108°,
故答案为:36°或90°或108°.
三.解答题
21.解:地图与该地区的实际图形相似,相似比就是比例尺为1:20,周长的比就是相似比,设实际周长是xcm,则
24:x=1:20,
解得:x=480,
面积的比等于相似比的平方,设实际面积是ycm2,则
20:y=(1:20)2,
解得y=8000,
答:这个区域的实际周长480cm,面积8000cm2.
22.解:设=k,
可得:x=2k,y=3k,z=4k,
把x=2k,y=3k,z=4k代入x﹣y+z=6,
可得:2k﹣3k+4k=6,
解得:k=2,
所以x=4,y=6,z=8,
把x=4,y=6,z=8代入3x﹣2y+z=12﹣12+8=8.
23.(1)解:
∵DE∥BC,
∴=,
又=,AE=3,
∴=,
解得AC=9,
∴EC=AC﹣AE=9﹣3=6;
(2)证明:
∵DE∥BC,EF∥CG,
∴==,
∴AD AG=AF AB.
24.解:设===k,
可得a=3k﹣4,b=2k﹣3,c=4k﹣8,
代入a+b+c=12得:9k﹣15=12,
解得:k=3,
∴a=5,b=3,c=4,
则△ABC为直角三角形.
25.解:设△ABC和△DEF的周长分别是x厘米和y厘米.
∵,
∴==①
由题意可得:y﹣x=15 ②
由①式得x=y③
将③式代入②式得:y﹣y=15,
∴y=45,
将y=45代入③式得:x=30,
答:△ABC和△DEF的周长分别是30厘米和45厘米.
26.解:(1)如图.
(2)探究:四边形EBCF是矩形,而且是黄金矩形.
∵四边形AEFD是正方形,
∴∠AEF=90°
∴∠BEF=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°
∴∠BEF=∠B=∠C=90°,
∴四边形EBCF是矩形.
【方法1】设
∴
∴矩形EBCF是黄金矩形.
【方法2】设,
∴
∴矩形EBCF是黄金矩形.
(3)归纳:在黄金矩形内以短边为边作一个正方形后,所得到的另外一个四边形是矩形,而且是黄金矩形.
27.证明:延长BA、EC,设交点为O,则四边形OADC为平行四边形,
∵F是AC的中点,
∴DF的延长线必过O点,且.
∵AB∥CD,
∴.
∵AD∥CE,
∴.
∴==.
又∵=,
∴OQ=3DN.
∴CQ=OQ﹣OC=3DN﹣OC=3DN﹣AD,AN=AD﹣DN.
∴AN+CQ=2DN.
∴==2.
即MN+PQ=2PN.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
