2021-2022学年苏科版数学八年级上册3.1勾股定理 课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级上册3.1勾股定理 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 832.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 16:15:02 | ||
图片预览




文档简介
(共16张PPT)
2002年国际数学家大会的会标
勾 股 定 理
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾股世界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
情境:走进历史--感受文化价值
让我们一起探索勾股定理吧
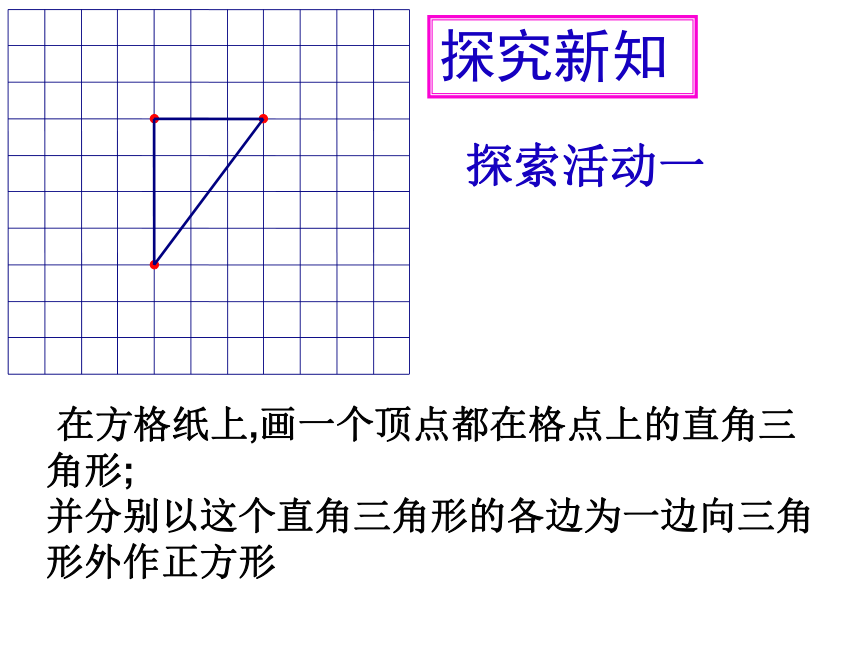
在方格纸上,画一个顶点都在格点上的直角三角形;
并分别以这个直角三角形的各边为一边向三角形外作正方形
探索活动一
探究新知
P
Q
C
R
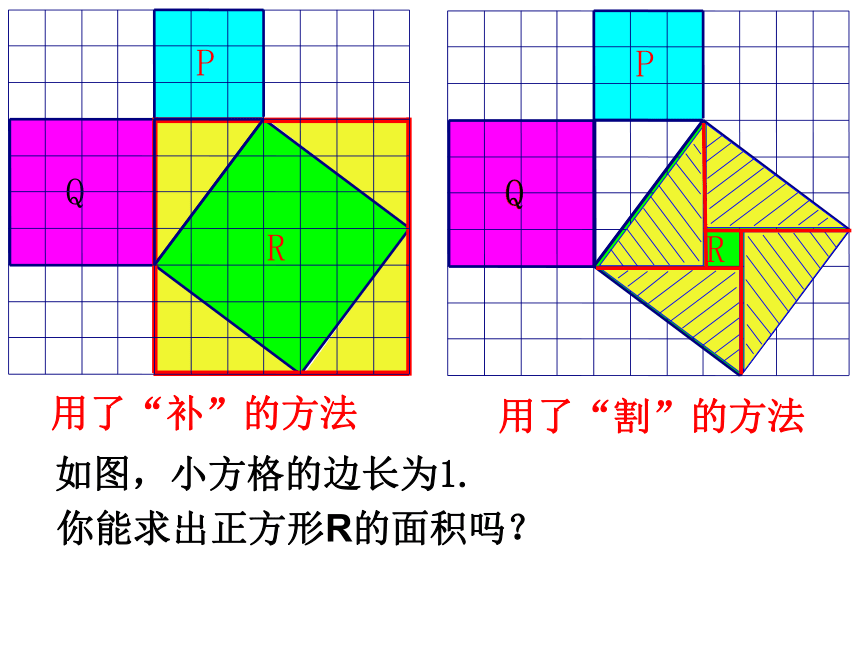
如图,小方格的边长为1.
(1)你能求出正方形R的面积吗?
用了“补”的方法
P
Q
C
R
用了“割”的方法
Q
P
Q
R
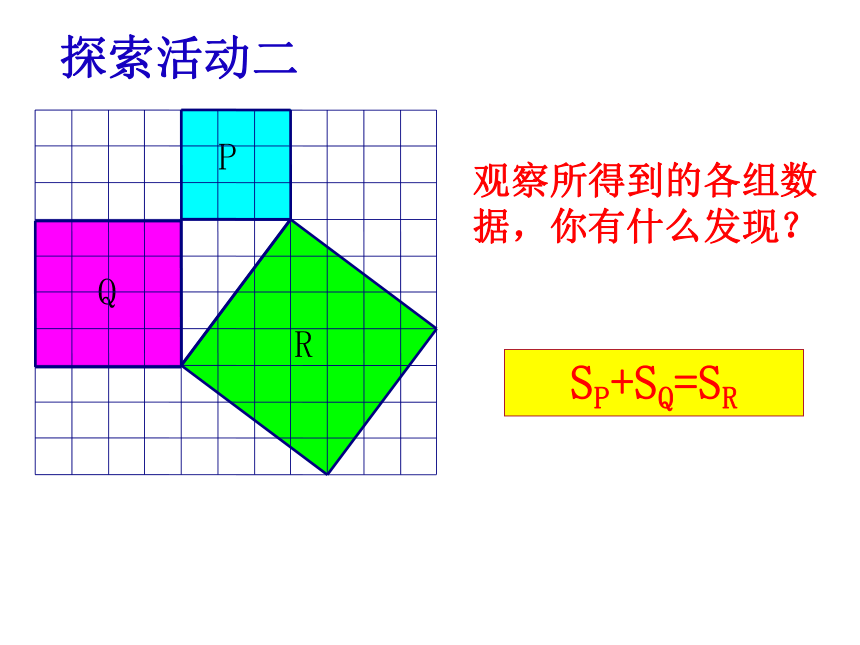
SP+SQ=SR
观察所得到的各组数据,你有什么发现?
探索活动二
图甲 图乙
A的面积
B的面积
C的面积
4
4
8
A
B
C
SA+SB=SC
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积 有 什 么关系?
A
B
C
C
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
P
Q
R
a
c
b
SP+SQ=SR
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?交流讨论
a2+b2=c2
SP=a2
SQ=b2
SR=c2
┏
a2+b2=c2
a
c
b
勾股定理 直角三角形两直角边的 平方和等于斜边的平方.
勾
股
弦
获得新知
比一比看看谁算得快!
1.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
应用新知
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
做一做
625
576
144
169
如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了几步路(假设2步为1米),却踩伤了花草?
解决问题
文明出行
试一试
1、如图,受台风 影响,一棵树在离地面4米
处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
C
B
A
已知,四边形ABCD中,∠DAB=∠DBC=90 ,AD=3,AB=4,BC=12。求:DC的长。
B
C
D
A
拓展延伸
通过今天的学习
你学到了哪些数学知识?
感受了哪些数学思想方法?
分享收获
2002年国际数学家大会的会标
勾 股 定 理
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾股世界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
情境:走进历史--感受文化价值
让我们一起探索勾股定理吧
在方格纸上,画一个顶点都在格点上的直角三角形;
并分别以这个直角三角形的各边为一边向三角形外作正方形
探索活动一
探究新知
P
Q
C
R
如图,小方格的边长为1.
(1)你能求出正方形R的面积吗?
用了“补”的方法
P
Q
C
R
用了“割”的方法
Q
P
Q
R
SP+SQ=SR
观察所得到的各组数据,你有什么发现?
探索活动二
图甲 图乙
A的面积
B的面积
C的面积
4
4
8
A
B
C
SA+SB=SC
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积 有 什 么关系?
A
B
C
C
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
P
Q
R
a
c
b
SP+SQ=SR
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?交流讨论
a2+b2=c2
SP=a2
SQ=b2
SR=c2
┏
a2+b2=c2
a
c
b
勾股定理 直角三角形两直角边的 平方和等于斜边的平方.
勾
股
弦
获得新知
比一比看看谁算得快!
1.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
应用新知
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
做一做
625
576
144
169
如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了几步路(假设2步为1米),却踩伤了花草?
解决问题
文明出行
试一试
1、如图,受台风 影响,一棵树在离地面4米
处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
C
B
A
已知,四边形ABCD中,∠DAB=∠DBC=90 ,AD=3,AB=4,BC=12。求:DC的长。
B
C
D
A
拓展延伸
通过今天的学习
你学到了哪些数学知识?
感受了哪些数学思想方法?
分享收获
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
