吉林省榆树一高2021-2022学年高二上学期10月月考数学试卷(Word版含答案)
文档属性
| 名称 | 吉林省榆树一高2021-2022学年高二上学期10月月考数学试卷(Word版含答案) | 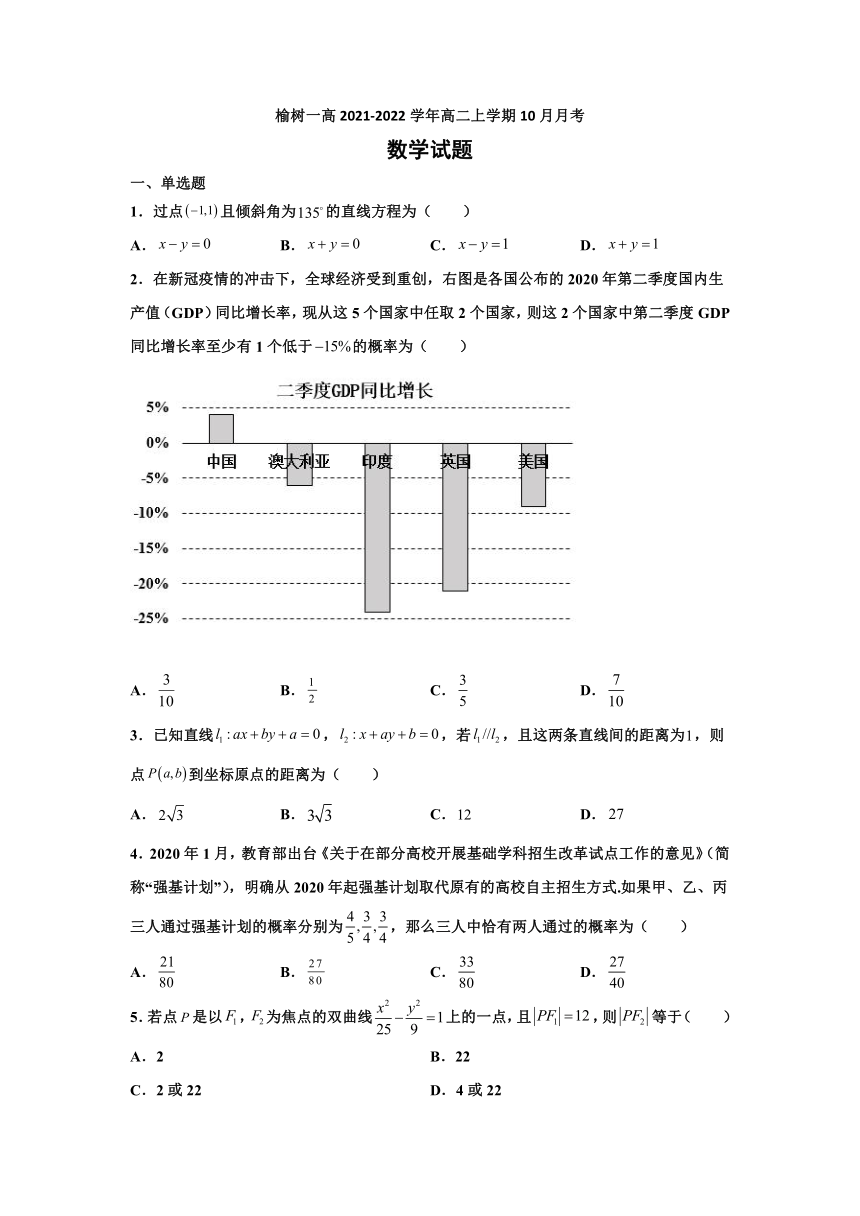 | |
| 格式 | doc | ||
| 文件大小 | 870.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 20:18:19 | ||
图片预览




文档简介
榆树一高2021-2022学年高二上学期10月月考
数学试题
一、单选题
1.过点且倾斜角为的直线方程为( )
A. B. C. D.
2.在新冠疫情的冲击下,全球经济受到重创,右图是各国公布的2020年第二季度国内生产值(GDP)同比增长率,现从这5个国家中任取2个国家,则这2个国家中第二季度GDP同比增长率至少有1个低于的概率为( )
A. B. C. D.
3.已知直线,,若,且这两条直线间的距离为,则点到坐标原点的距离为( )
A. B. C. D.
4.2020年1月,教育部出台《关于在部分高校开展基础学科招生改革试点工作的意见》(简称“强基计划”),明确从2020年起强基计划取代原有的高校自主招生方式.如果甲、乙、丙三人通过强基计划的概率分别为,那么三人中恰有两人通过的概率为( )
A. B. C. D.
5.若点是以,为焦点的双曲线上的一点,且,则等于( )
A.2 B.22
C.2或22 D.4或22
6.如果圆上总存在到原点的距离为的点,则实数的取值范围是
A. B. C. D.
7.已知点是直线()上一动点,,是圆:的两条切线,,为切点,若四边形的最小面积是2,则的值为( )
A.4 B. C.2 D.
8.已知椭圆与圆在第二象限的交点是点,是椭圆的左焦点,为坐标原点,到直线的距离是,则椭圆的离心率是( )
A. B. C. D.
二、多选题
9.设,为两个随机事件,以下命题正确的为( )
A.若,是互斥事件,,,则
B.若,是对立事件,则
C.若,是独立事件,,,则
D.若,,且,则,是独立事件
10.以下四个命题表述正确的是
A.直线恒过定点
B.圆:的圆心到直线的距离为2
C.圆:与圆:恰有三条公切线
D.两圆与的公共弦所在的直线方程为:
11.若直线过点,且在两坐标轴上截距的绝对值相等,则直线方程可能为( )
A. B.
C. D.
12.动点分别到两定点连线的斜率的乘积为,设的轨迹为曲线,分别为曲线的左、右焦点,则下列命题中正确的有( )
A.曲线的焦点坐标为;
B.若,则;
C.的内切圆的面积的最大值为;
D.设,则的最小值为.
三、填空题
13.在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球,分别标有数字1,2,3,4.现每次有放回地从中任意取出一个小球,直到标有偶数的球都取到过就停止.小明用随机模拟的方法估计恰好在第3次停止摸球的概率,利用计算机软件产生随机数,每1组中有3个数字,分别表示每次摸球的结果,经随机模拟产生了以下18组随机数:
131 432 123 233 234 122 332 141 312 241 122 214 431 241 141 433 223 442
由此可以估计恰好在第3次停止摸球的概率为_________
14.已知m为实数,直线,,若,则实数m的值为________.
15.已知双曲线与椭圆有共同的焦点,且它们的离心率之和为,则双曲线的方程是_______
16.若过点可作圆的两条切线,则实数的取值范围为________.
四、解答题
17.已知的顶点,边上的中线所在直线方程为,边上的高所在直线方程为,
(1)求顶点的坐标;
(2)求的面积.
18.某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在[120,130)内的频率;
(2)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
19.在①圆经过,②圆心在直线上,③圆截轴所得弦长为8且圆心的坐标为整数;这三个条件中任选一个,补充在下面的问题中,进行求解.
已知圆经过点,且______;
(1)求圆的方程;
(2)已知直线经过点,直线与圆相交所得的弦长为8,求直线的方程.
20.已知椭圆的左焦点到圆上一点距离的最大值为6,且过椭圆右焦点与上顶点的直线与圆相切.
(1)求椭圆的方程;
(2)若直线与椭圆交于A,两点,当以为直径的圆与轴相切时,求的值.
答案
选择:1-8 BDACC DCB 9.BCD 10.AC 11.ABC 12.ACD
13. 14.1 15. 16.
17. 【答案】(1);(2).
【详解】
(1)设,因为直线与直线垂直,且点在直线上,
所以,解得,故.
(2)设由题知:,
所以,解得,即.
,直线,即:.
,
点到直线的距离,
所以.
18. 【答案】(1)0.3;(2).
【详解】
解:(1)分数在内的频率为.
(2)由题意知,[110,120)分数段的人数为60×0.15=9,[120,130)分数段的人数为60×0.3=18.
用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,则需在[110,120)分数段内抽取2人,并分别记为m,n,在[120,130)分数段内抽取4人,并分别记为a,b,c,d.
设“从样本中任取2人,至多有1人在分数段[120,130)内”为事件A.
易知基本事件有(m,n),(m,a),(m,b), (m,c),(m,d),(n,a),(n,b),(n,c),(n,d),(a,b),(a,c),(a,d),(b,c) ,(b,d),(c,d)共15种.
事件A包含的基本事件有(m,n),(m,a),(m,b),(m,c),(m,d),(n,a),(n,b),(n,c),(n,d),共9种.
故P(A)==.
19. 【答案】(1);(2)或
【详解】
解:选条件①,
(1)设圆的方程为,
依题意有, 解得,,,
所以圆的方程为, 即圆的标准方程为:.
(2)设圆心到直线的距离为, 则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,,解得,,
所以所求直线的方程为或.
选条件②,
(1)设圆的方程为,
因为圆经过点,,且圆心在直线上
依题意有,解得,,,
所以圆的方程为.
(2)设圆心到直线的距离为, 则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,,解得,,
所以所求直线的方程为或.
选条件③,
设圆的方程为,
由圆经过点,,故, 又因为圆截轴所得弦长为8,
故方程的两个实数根的差的绝对值为.
所以,即
解方程组,得,,或,,,
由于圆心的坐标为整数,故圆的方程为
(2)设圆心到直线的距离为,则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,,解得,,
所以所求直线的方程为或.
20. 【答案】(1);(2)或.
【详解】
(1)椭圆的左焦点到圆上一点距离的最大值为,又,所以.
过椭圆右焦点和上顶点的直线方程为,即,
由直线和圆相切可得,解得, 所以.
所以椭圆的方程为.
(2)由,可得, 则,即.
设,,则,, 所以中点的横坐标为,
则以为直径的圆的半径为.
因为该圆与y轴相切,所以,
整理可得,即, 解得,所以或.
数学试题
一、单选题
1.过点且倾斜角为的直线方程为( )
A. B. C. D.
2.在新冠疫情的冲击下,全球经济受到重创,右图是各国公布的2020年第二季度国内生产值(GDP)同比增长率,现从这5个国家中任取2个国家,则这2个国家中第二季度GDP同比增长率至少有1个低于的概率为( )
A. B. C. D.
3.已知直线,,若,且这两条直线间的距离为,则点到坐标原点的距离为( )
A. B. C. D.
4.2020年1月,教育部出台《关于在部分高校开展基础学科招生改革试点工作的意见》(简称“强基计划”),明确从2020年起强基计划取代原有的高校自主招生方式.如果甲、乙、丙三人通过强基计划的概率分别为,那么三人中恰有两人通过的概率为( )
A. B. C. D.
5.若点是以,为焦点的双曲线上的一点,且,则等于( )
A.2 B.22
C.2或22 D.4或22
6.如果圆上总存在到原点的距离为的点,则实数的取值范围是
A. B. C. D.
7.已知点是直线()上一动点,,是圆:的两条切线,,为切点,若四边形的最小面积是2,则的值为( )
A.4 B. C.2 D.
8.已知椭圆与圆在第二象限的交点是点,是椭圆的左焦点,为坐标原点,到直线的距离是,则椭圆的离心率是( )
A. B. C. D.
二、多选题
9.设,为两个随机事件,以下命题正确的为( )
A.若,是互斥事件,,,则
B.若,是对立事件,则
C.若,是独立事件,,,则
D.若,,且,则,是独立事件
10.以下四个命题表述正确的是
A.直线恒过定点
B.圆:的圆心到直线的距离为2
C.圆:与圆:恰有三条公切线
D.两圆与的公共弦所在的直线方程为:
11.若直线过点,且在两坐标轴上截距的绝对值相等,则直线方程可能为( )
A. B.
C. D.
12.动点分别到两定点连线的斜率的乘积为,设的轨迹为曲线,分别为曲线的左、右焦点,则下列命题中正确的有( )
A.曲线的焦点坐标为;
B.若,则;
C.的内切圆的面积的最大值为;
D.设,则的最小值为.
三、填空题
13.在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球,分别标有数字1,2,3,4.现每次有放回地从中任意取出一个小球,直到标有偶数的球都取到过就停止.小明用随机模拟的方法估计恰好在第3次停止摸球的概率,利用计算机软件产生随机数,每1组中有3个数字,分别表示每次摸球的结果,经随机模拟产生了以下18组随机数:
131 432 123 233 234 122 332 141 312 241 122 214 431 241 141 433 223 442
由此可以估计恰好在第3次停止摸球的概率为_________
14.已知m为实数,直线,,若,则实数m的值为________.
15.已知双曲线与椭圆有共同的焦点,且它们的离心率之和为,则双曲线的方程是_______
16.若过点可作圆的两条切线,则实数的取值范围为________.
四、解答题
17.已知的顶点,边上的中线所在直线方程为,边上的高所在直线方程为,
(1)求顶点的坐标;
(2)求的面积.
18.某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在[120,130)内的频率;
(2)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
19.在①圆经过,②圆心在直线上,③圆截轴所得弦长为8且圆心的坐标为整数;这三个条件中任选一个,补充在下面的问题中,进行求解.
已知圆经过点,且______;
(1)求圆的方程;
(2)已知直线经过点,直线与圆相交所得的弦长为8,求直线的方程.
20.已知椭圆的左焦点到圆上一点距离的最大值为6,且过椭圆右焦点与上顶点的直线与圆相切.
(1)求椭圆的方程;
(2)若直线与椭圆交于A,两点,当以为直径的圆与轴相切时,求的值.
答案
选择:1-8 BDACC DCB 9.BCD 10.AC 11.ABC 12.ACD
13. 14.1 15. 16.
17. 【答案】(1);(2).
【详解】
(1)设,因为直线与直线垂直,且点在直线上,
所以,解得,故.
(2)设由题知:,
所以,解得,即.
,直线,即:.
,
点到直线的距离,
所以.
18. 【答案】(1)0.3;(2).
【详解】
解:(1)分数在内的频率为.
(2)由题意知,[110,120)分数段的人数为60×0.15=9,[120,130)分数段的人数为60×0.3=18.
用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,则需在[110,120)分数段内抽取2人,并分别记为m,n,在[120,130)分数段内抽取4人,并分别记为a,b,c,d.
设“从样本中任取2人,至多有1人在分数段[120,130)内”为事件A.
易知基本事件有(m,n),(m,a),(m,b), (m,c),(m,d),(n,a),(n,b),(n,c),(n,d),(a,b),(a,c),(a,d),(b,c) ,(b,d),(c,d)共15种.
事件A包含的基本事件有(m,n),(m,a),(m,b),(m,c),(m,d),(n,a),(n,b),(n,c),(n,d),共9种.
故P(A)==.
19. 【答案】(1);(2)或
【详解】
解:选条件①,
(1)设圆的方程为,
依题意有, 解得,,,
所以圆的方程为, 即圆的标准方程为:.
(2)设圆心到直线的距离为, 则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,,解得,,
所以所求直线的方程为或.
选条件②,
(1)设圆的方程为,
因为圆经过点,,且圆心在直线上
依题意有,解得,,,
所以圆的方程为.
(2)设圆心到直线的距离为, 则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,,解得,,
所以所求直线的方程为或.
选条件③,
设圆的方程为,
由圆经过点,,故, 又因为圆截轴所得弦长为8,
故方程的两个实数根的差的绝对值为.
所以,即
解方程组,得,,或,,,
由于圆心的坐标为整数,故圆的方程为
(2)设圆心到直线的距离为,则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,,解得,,
所以所求直线的方程为或.
20. 【答案】(1);(2)或.
【详解】
(1)椭圆的左焦点到圆上一点距离的最大值为,又,所以.
过椭圆右焦点和上顶点的直线方程为,即,
由直线和圆相切可得,解得, 所以.
所以椭圆的方程为.
(2)由,可得, 则,即.
设,,则,, 所以中点的横坐标为,
则以为直径的圆的半径为.
因为该圆与y轴相切,所以,
整理可得,即, 解得,所以或.
同课章节目录
