北师大版高中数学必修1《二次函数的图象》教学课件(共19张PPT)
文档属性
| 名称 | 北师大版高中数学必修1《二次函数的图象》教学课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 17:06:23 | ||
图片预览





文档简介
(共19张PPT)
? §4 二次函数性质的再研究
4.1 二次函数的图象
1.函数y=2x+1的图象与y轴的交点为 ,其单调性为 .
2.函数y=x2-2x+1的开口方向向 ,顶点坐标为 ,对称轴为 ,单调增区间为 ,单调减区间为 .
(0,1)
在(-∞,+∞)上是增函数
上
(1,0)
x=1
[1,+∞)
(-∞,1]
二次函数图象间的变换
(1)y=x2与y=ax2(a≠0)间的变换
纵坐标
a
左
h
上
k
右
下
在二次函数y=a(x+h)2+k(a≠0)的图象变换中,参数“a,h,k”的作用分别是什么?
【提示】 ①a的符号和绝对值大小分别决定了二次函数图象的开口方向和大小;②h决定了二次函数图象的左、右平移,而且“h正左移,h负右移”;③k决定了二次函数图象的上、下平移,而且“k正上移,k负下移”.
二次函数的图象的平移
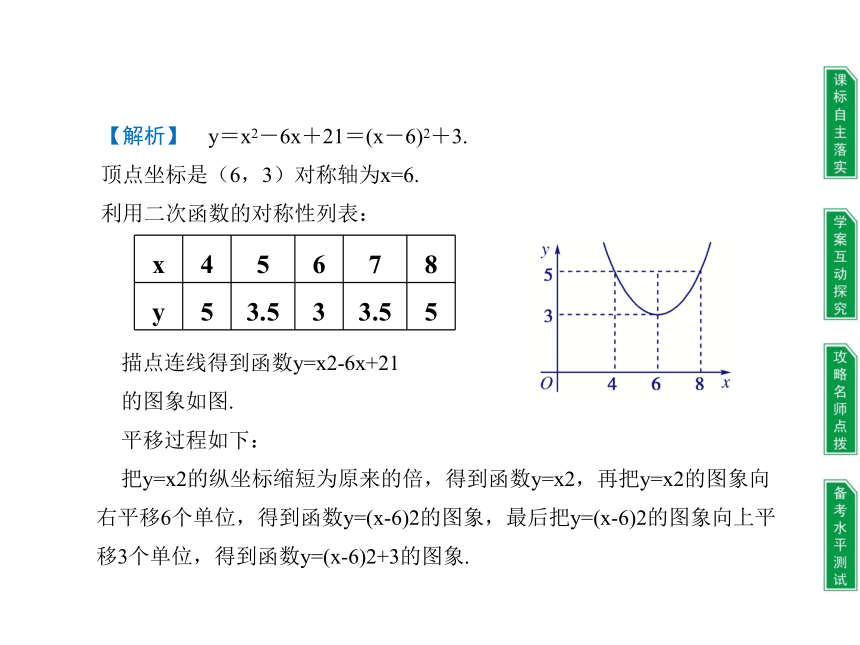
【解析】 y=x2-6x+21=(x-6)2+3.
顶点坐标是(6,3)对称轴为x=6.
利用二次函数的对称性列表:
x 4 5 6 7 8
y 5 3.5 3 3.5 5
描点连线得到函数y=x2-6x+21
的图象如图.
平移过程如下:
把y=x2的纵坐标缩短为原来的倍,得到函数y=x2,再把y=x2的图象向右平移6个单位,得到函数y=(x-6)2的图象,最后把y=(x-6)2的图象向上平移3个单位,得到函数y=(x-6)2+3的图象.
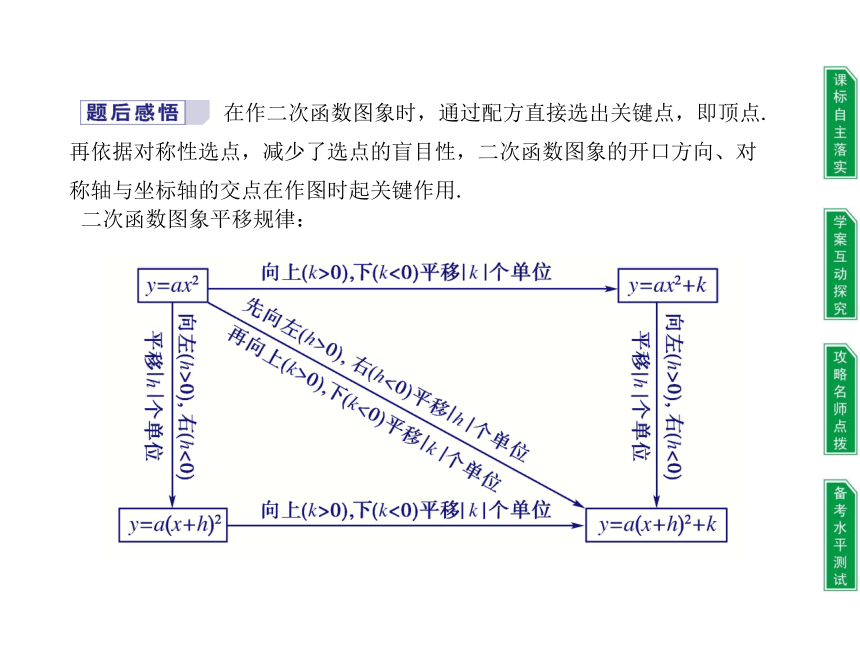
在作二次函数图象时,通过配方直接选出关键点,即顶点.再依据对称性选点,减少了选点的盲目性,二次函数图象的开口方向、对称轴与坐标轴的交点在作图时起关键作用.
二次函数图象平移规律:
1.函数y=x2的图象 平移 个单位长度,得到函数y=(x+2)2的图象,再 平移 个单位长度,得到函数y=(x+2)2-1的图象.若想要变回原来的函数,则需 平移 个单位长度,再 平移 个单位长度.
【答案】 向左 2 向下 1 向上 1 向右 2
求二次函数的解析式
二次函数的顶点坐标是(2,3),且经过点(3,1),求这个二次函数的解析式.
【思路点拨】 二次函数的一般式是y=ax2+bx+c,其中a、b、c为待定系数,应当根据三个条件,列出三个方程,进而求出待定的系数,写出函数解析式,本题给出的顶点坐标(2,3)还隐含着图象的对称轴x=2这样一个条件,即 .
方法二:二次函数的顶点式是y=a(x-h)2+k,而顶点坐标是(2,3),故有y=a(x-2)2+3,这样只需确定a的值.因为图象经过点(3,1),所以x=3,y=1满足于关系式y=a(x-2)2+3,从而有1=a(3-2)2+3,解得a=-2.
∴函数解析式为y=-2(x-2)2+3,
即y=-2x2+8x-5.
方法二:二次函数的顶点式是y=a(x-h)2+k,而顶点坐标是(2,3),故有y=a(x-2)2+3,这样只需确定a的值.因为图象经过点(3,1),所以x=3,y=1满足于关系式y=a(x-2)2+3,从而有1=a(3-2)2+3,解得a=-2.
∴函数解析式为y=-2(x-2)2+3,
即y=-2x2+8x-5.
运用待定系数法求二次函数的解析式时,一般可设出二次函数的一般式y=ax2+bx+c(a≠0),但如果已知函数的对称轴、顶点坐标或最值,则将解析式设为y=(x-h)2+k会使求解更加方便.具体来说:
(1)已知顶点坐标为(m,n),可设y=a(x-m)2+n,再借助于其他条件求a;
(2)已知对称轴方程x=m,可设y=a(x-m)2+k,再借助于其他条件求a和k;
(3)已知最大值或最小值为n,可设y=a(x-h)2+n,再借助于其他条件求a和h;
(4)二次函数的图象与x轴只有一个交点时,可设y=a(x-h)2,再借助于其他条件求a和h.
2.已知二次函数y=f(x)满足以下条件,求该函数的解析式:
(1)图象过A(0,1),B(1,2),C(2,-1)三点;
(2)图象顶点是(-2,3),且过点(-1,5).
1.五点法作二次函数图象的步骤
①确定顶点坐标,画出对称轴;
②找出关于对称轴对称的四个点;
③用平滑曲线连接五个点.
如何平移抛物线y=2x2可得到抛物线y=2(x+4)2+k?
【错解】 要得到y=2(x+4)2+k的图象,只需将y=2x2的图象向左平移4个单位
【错因】 没有对k进行讨论,k的正负、上下是不同的.
【正解】 要得到y=2(x+4)2+k的图象,只需将y=2x2的图象向左平移4个单位,当k>0时,向上平移k个单位,当k=0时,不作平移,当k<0时,向下平移|k|个单位.
1.二次函数y=x2的图象上各点的纵坐标变为原来的2倍,得到的新图象的二次函数是 ( )
?A.?y=x2+2 B.?y=2x2
?C.?y= x2 ? D.?y=x2-2
【答案】 ?B?
2.函数y= x2-5x+1的对称轴和顶点坐标分别是 ( )
?A.?x=5, ?B.?x=-5,
?C.?x=5, ?D.?x=-5,
【答案】 ?A?
3.二次函数的顶点坐标为(2,-1),且过点(3,1),则解析式为 .
【答案】 y=2x2-8x+7
4.对于二次函数y=-x2+4x+3,
(1)指出图象的开口方向、对称轴方程、顶点坐标.
(2)说明其图象是由y=-x2的图象经过怎样的平移得来?
【解析】 ∵y=-(x-2)2+7,
∴(1)开口向下;对称轴方程为x=2;顶点坐标为(2,7);
(2)先将y=-x2的图象向右平移2个单位,然后再向上平移7个单位,即可得到y=-x2+4x+3的图象.
? §4 二次函数性质的再研究
4.1 二次函数的图象
1.函数y=2x+1的图象与y轴的交点为 ,其单调性为 .
2.函数y=x2-2x+1的开口方向向 ,顶点坐标为 ,对称轴为 ,单调增区间为 ,单调减区间为 .
(0,1)
在(-∞,+∞)上是增函数
上
(1,0)
x=1
[1,+∞)
(-∞,1]
二次函数图象间的变换
(1)y=x2与y=ax2(a≠0)间的变换
纵坐标
a
左
h
上
k
右
下
在二次函数y=a(x+h)2+k(a≠0)的图象变换中,参数“a,h,k”的作用分别是什么?
【提示】 ①a的符号和绝对值大小分别决定了二次函数图象的开口方向和大小;②h决定了二次函数图象的左、右平移,而且“h正左移,h负右移”;③k决定了二次函数图象的上、下平移,而且“k正上移,k负下移”.
二次函数的图象的平移
【解析】 y=x2-6x+21=(x-6)2+3.
顶点坐标是(6,3)对称轴为x=6.
利用二次函数的对称性列表:
x 4 5 6 7 8
y 5 3.5 3 3.5 5
描点连线得到函数y=x2-6x+21
的图象如图.
平移过程如下:
把y=x2的纵坐标缩短为原来的倍,得到函数y=x2,再把y=x2的图象向右平移6个单位,得到函数y=(x-6)2的图象,最后把y=(x-6)2的图象向上平移3个单位,得到函数y=(x-6)2+3的图象.
在作二次函数图象时,通过配方直接选出关键点,即顶点.再依据对称性选点,减少了选点的盲目性,二次函数图象的开口方向、对称轴与坐标轴的交点在作图时起关键作用.
二次函数图象平移规律:
1.函数y=x2的图象 平移 个单位长度,得到函数y=(x+2)2的图象,再 平移 个单位长度,得到函数y=(x+2)2-1的图象.若想要变回原来的函数,则需 平移 个单位长度,再 平移 个单位长度.
【答案】 向左 2 向下 1 向上 1 向右 2
求二次函数的解析式
二次函数的顶点坐标是(2,3),且经过点(3,1),求这个二次函数的解析式.
【思路点拨】 二次函数的一般式是y=ax2+bx+c,其中a、b、c为待定系数,应当根据三个条件,列出三个方程,进而求出待定的系数,写出函数解析式,本题给出的顶点坐标(2,3)还隐含着图象的对称轴x=2这样一个条件,即 .
方法二:二次函数的顶点式是y=a(x-h)2+k,而顶点坐标是(2,3),故有y=a(x-2)2+3,这样只需确定a的值.因为图象经过点(3,1),所以x=3,y=1满足于关系式y=a(x-2)2+3,从而有1=a(3-2)2+3,解得a=-2.
∴函数解析式为y=-2(x-2)2+3,
即y=-2x2+8x-5.
方法二:二次函数的顶点式是y=a(x-h)2+k,而顶点坐标是(2,3),故有y=a(x-2)2+3,这样只需确定a的值.因为图象经过点(3,1),所以x=3,y=1满足于关系式y=a(x-2)2+3,从而有1=a(3-2)2+3,解得a=-2.
∴函数解析式为y=-2(x-2)2+3,
即y=-2x2+8x-5.
运用待定系数法求二次函数的解析式时,一般可设出二次函数的一般式y=ax2+bx+c(a≠0),但如果已知函数的对称轴、顶点坐标或最值,则将解析式设为y=(x-h)2+k会使求解更加方便.具体来说:
(1)已知顶点坐标为(m,n),可设y=a(x-m)2+n,再借助于其他条件求a;
(2)已知对称轴方程x=m,可设y=a(x-m)2+k,再借助于其他条件求a和k;
(3)已知最大值或最小值为n,可设y=a(x-h)2+n,再借助于其他条件求a和h;
(4)二次函数的图象与x轴只有一个交点时,可设y=a(x-h)2,再借助于其他条件求a和h.
2.已知二次函数y=f(x)满足以下条件,求该函数的解析式:
(1)图象过A(0,1),B(1,2),C(2,-1)三点;
(2)图象顶点是(-2,3),且过点(-1,5).
1.五点法作二次函数图象的步骤
①确定顶点坐标,画出对称轴;
②找出关于对称轴对称的四个点;
③用平滑曲线连接五个点.
如何平移抛物线y=2x2可得到抛物线y=2(x+4)2+k?
【错解】 要得到y=2(x+4)2+k的图象,只需将y=2x2的图象向左平移4个单位
【错因】 没有对k进行讨论,k的正负、上下是不同的.
【正解】 要得到y=2(x+4)2+k的图象,只需将y=2x2的图象向左平移4个单位,当k>0时,向上平移k个单位,当k=0时,不作平移,当k<0时,向下平移|k|个单位.
1.二次函数y=x2的图象上各点的纵坐标变为原来的2倍,得到的新图象的二次函数是 ( )
?A.?y=x2+2 B.?y=2x2
?C.?y= x2 ? D.?y=x2-2
【答案】 ?B?
2.函数y= x2-5x+1的对称轴和顶点坐标分别是 ( )
?A.?x=5, ?B.?x=-5,
?C.?x=5, ?D.?x=-5,
【答案】 ?A?
3.二次函数的顶点坐标为(2,-1),且过点(3,1),则解析式为 .
【答案】 y=2x2-8x+7
4.对于二次函数y=-x2+4x+3,
(1)指出图象的开口方向、对称轴方程、顶点坐标.
(2)说明其图象是由y=-x2的图象经过怎样的平移得来?
【解析】 ∵y=-(x-2)2+7,
∴(1)开口向下;对称轴方程为x=2;顶点坐标为(2,7);
(2)先将y=-x2的图象向右平移2个单位,然后再向上平移7个单位,即可得到y=-x2+4x+3的图象.
