《24.4 相似三角形判定》同步练习2020-2021学年 沪教版九年级数学上册(Word版 含解析)
文档属性
| 名称 | 《24.4 相似三角形判定》同步练习2020-2021学年 沪教版九年级数学上册(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 470.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 11:03:03 | ||
图片预览



文档简介
24.4 相似三角形判定
一.填空题
1.如图,已知∠ADE=∠ACD=∠ABC,则图中相似三角形共有 对.
2.已知,如图,CD是Rt△ACB斜边上的高,若AD=6,BD=2,CE=3,则BC的长度为 ;BE的长度为 .
3.如图,若AD AB=AE AC,∠A=70°,∠AED=54°,则∠C= 度.
4.如图,已知Rt△ACB中,∠C=90°,四边形MNPQ是正方形,若AN=4,BP=6,则PQ= .
5.已知,如图,AB⊥AC,AC⊥CD,M为线段AC上一动点,AB=4cm,AC=11cm,CD=6cm,当AM= 时,△ABM与以M,C,D构成的三角形相似.
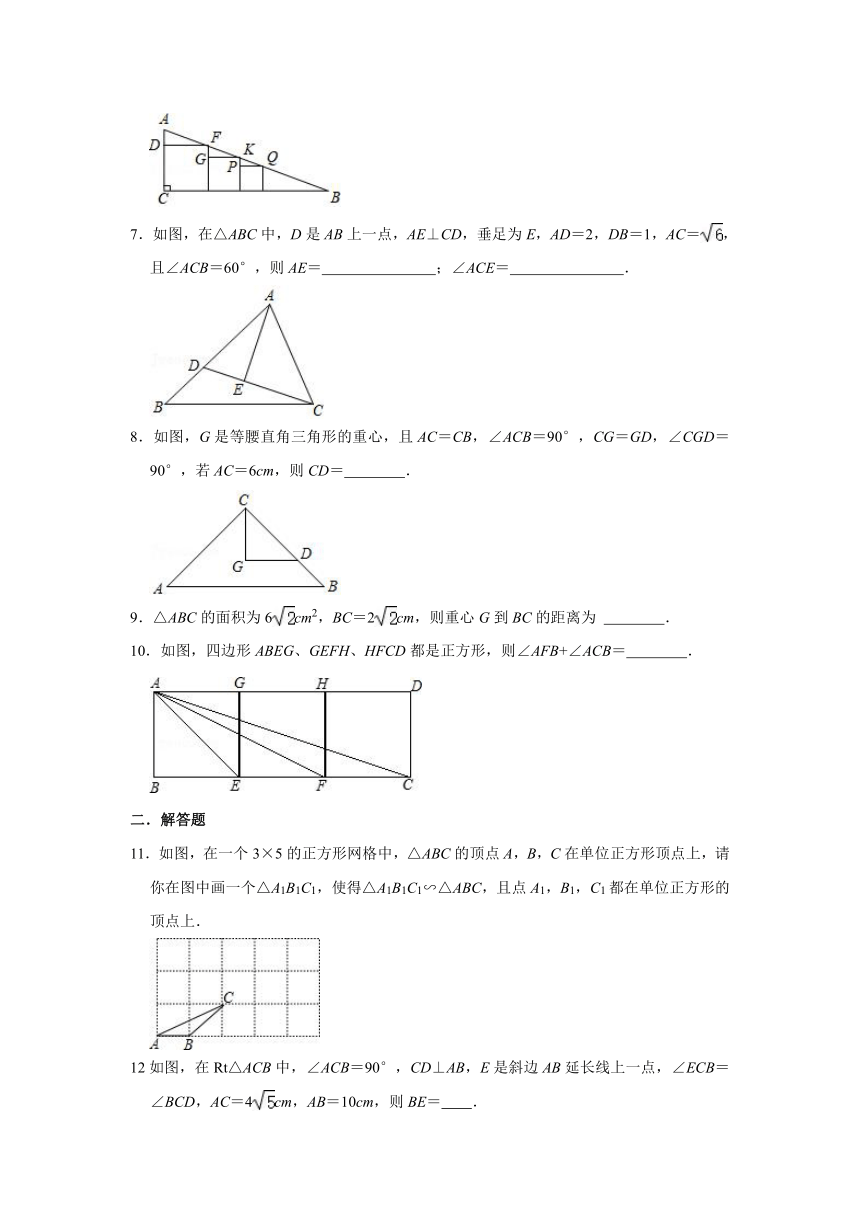
6.如图,Rt△ABC内有三个正方形,DF=9cm,GK=6cm,则PQ的长是 .
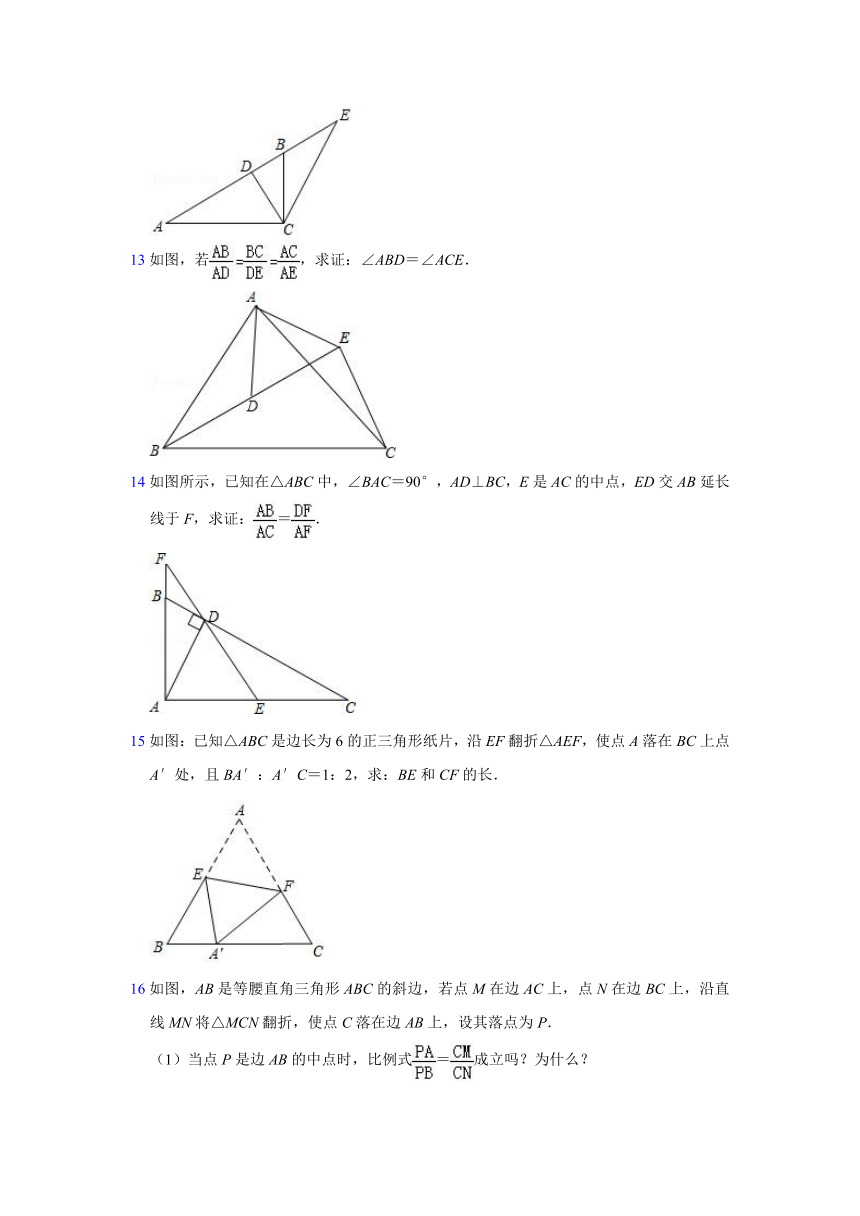
7.如图,在△ABC中,D是AB上一点,AE⊥CD,垂足为E,AD=2,DB=1,AC=,且∠ACB=60°,则AE= ;∠ACE= .
8.如图,G是等腰直角三角形的重心,且AC=CB,∠ACB=90°,CG=GD,∠CGD=90°,若AC=6cm,则CD= .
9.△ABC的面积为6cm2,BC=2cm,则重心G到BC的距离为 .
10.如图,四边形ABEG、GEFH、HFCD都是正方形,则∠AFB+∠ACB= .
二.解答题
11.如图,在一个3×5的正方形网格中,△ABC的顶点A,B,C在单位正方形顶点上,请你在图中画一个△A1B1C1,使得△A1B1C1∽△ABC,且点A1,B1,C1都在单位正方形的顶点上.
12如图,在Rt△ACB中,∠ACB=90°,CD⊥AB,E是斜边AB延长线上一点,∠ECB=∠BCD,AC=4cm,AB=10cm,则BE= .
13如图,若,求证:∠ABD=∠ACE.
14如图所示,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB延长线于F,求证:=.
15如图:已知△ABC是边长为6的正三角形纸片,沿EF翻折△AEF,使点A落在BC上点A′处,且BA′:A′C=1:2,求:BE和CF的长.
16如图,AB是等腰直角三角形ABC的斜边,若点M在边AC上,点N在边BC上,沿直线MN将△MCN翻折,使点C落在边AB上,设其落点为P.
(1)当点P是边AB的中点时,比例式=成立吗?为什么?
(2)当点P不是边AB的中点时,=是否仍然成立?请说明理由.
17在平面直角坐标系中,已知点A(4,0),点B(0,3).点P从点A出发,以每秒1个单位的速度向右平移,点Q从点B出发,以每秒2个单位的速度向右平移,又P、Q两点同时出发.
(1)连接AQ,当△ABQ是直角三角形时,求点Q的坐标;
(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时∠AQP的度数;
(3)过点A作AC⊥AB,AC交射线PQ于点C,连接BC,D是BC的中点.在点P、Q的运动过程中,是否存在某时刻,使得以A、C、Q、D为顶点的四边形是平行四边形?若存在,试求出这时cot∠ABC的值;若不存在,试说明理由.
参考答案与试题解析
一.填空题
1.如图,已知∠ADE=∠ACD=∠ABC,则图中相似三角形共有 4 对.
【分析】根据已知先判定线段DE∥BC,再根据相似三角形的判定方法进行分析,从而得到答案.
【解答】解:∵∠ADE=∠ACD=∠ABC,
∴DE∥BC.
∴△ADE∽△ABC,
∵DE∥BC,
∴∠EDC=∠DCB,
∵∠ACD=∠ABC,
∴△EDC∽△DCB,
同理:∠ACD=∠ABC,∠A=∠A,
∴△ABC∽△ACD,
∵△ADE∽△ABC,△ABC∽△ACD,
∴△ADE∽△ACD.
∴共4对.
故答案是:4.
2.已知,如图,CD是Rt△ACB斜边上的高,若AD=6,BD=2,CE=3,则BC的长度为 4 ;BE的长度为 5 .
【分析】根据“CD是Rt△ACB斜边上的高”证得△CDB∽△ACB,进而得到BC2=BD AB,即可求得BC,再利用勾股定理即可得到BE.
【解答】解:∵CD是Rt△ACB斜边上的高,
∴∠CDB=∠ACB=90°,
∵∠DBC=∠CBA,
∴△CDB∽△ACB,
∴=,即BC2=BD AB,
∵AD=6,BD=2,
∴AB=AD+BD=8,
∴BC=4,
在Rt△BCE中,BC=4,CE=3,
∴BE=5.
故答案为:4,5.
3.如图,若AD AB=AE AC,∠A=70°,∠AED=54°,则∠C= 56 度.
【分析】利用相似三角形的判定方法可判断△ADE∽△ACB,则∠ADE=∠C,然后利用三角形内角和计算出∠ADE,从而得到∠C的度数.
【解答】解:∵AD AB=AE AC,
∴=,
而∠DAE=∠CAB,
∴△ADE∽△ACB,
∴∠ADE=∠C,
∵∠ADE=180°﹣∠A﹣∠AED=180°﹣70°﹣54°=56°.
故答案为56.
4.如图,已知Rt△ACB中,∠C=90°,四边形MNPQ是正方形,若AN=4,BP=6,则PQ= 2 .
【分析】设PQ=x,证明△AMN∽△QBP,则利用相似比得到=,即=,然后利用比例性质求出x即可.
【解答】解:设PQ=x,
∵四边形MNPQ是正方形,
∴MN=PQ=x,∠MNP=∠QPN=90°,
∵∠C=90°,
∴∠A+∠B=90°,
而∠A+∠AMN=90°,
∴∠AMN=∠B,
∵∠ANM=∠BPQ,
∴△AMN∽△QBP,
∴=,即=,解得x=2或x=﹣2(舍去),
∴PQ=2.
故答案为2.
5.已知,如图,AB⊥AC,AC⊥CD,M为线段AC上一动点,AB=4cm,AC=11cm,CD=6cm,当AM= cm 时,△ABM与以M,C,D构成的三角形相似.
【分析】首先判定△ABM∽△CDM,然后由该相似三角形的对应边相等得到:=,代入相关数值即可解答.
【解答】解:∵△ABM与以M,C,D构成的三角形相似,且∠AMB=∠CMB,
∴△ABM∽△CDM或△ABM∽△DCM,
如图,∵AB⊥AC,AC⊥CD,
∴AB∥CD.
∴只有△ABM∽△CDM.
∴=.
∵AB=4cm,AC=11cm,CD=6cm,
∴=.
∴AM=(cm).
故答案是:cm.
6.如图,Rt△ABC内有三个正方形,DF=9cm,GK=6cm,则PQ的长是 4cm .
【分析】由相似三角形的判定可得△QPK∽△KGF∽△FDA,由相似三角形的性质可得=,再由正方形的性质可得:PK=KQ﹣QP,GF=DF﹣GK,即可求得PQ的长度.
【解答】解:由已知可得PK∥EF∥AC,
∴△QPK∽△KGF∽△FDA,
∴由相似三角形的性质和正方形的性质可得:=,
又∵PK=KG﹣QP,GF=DF﹣GK,DF=9cm,GK=6cm
∴=,即=,
解得:QP=4.
则PQ的长是4cm;
故答案为:4cm.
7.如图,在△ABC中,D是AB上一点,AE⊥CD,垂足为E,AD=2,DB=1,AC=,且∠ACB=60°,则AE= ;∠ACE= 45° .
【分析】根据“AD=2,DB=1,AC=”得到AC2=AD AB,进而证得△ACD∽△ABC,利用特殊角的锐角三角函数可得AE,再利用勾股定理求得CE,可得AE=CE,即可求得∠ACE.
【解答】解:∵AD=2,DB=1,
∴AB=AD+DB=3,
∵AC=,
∴AC2=AD AB,
∵∠DAC=∠CAB,
∴△ACD∽△ABC,
∴∠ADC=∠ACB=60°,
在Rt△ADE中,AD=2,∠ADC=60°,
∴AE=,
在Rt△ACE中,AE=,AC=,
∴CE=,
∴AE=CE,
∴∠ACE=45°.
故答案为:,45°.
8.如图,G是等腰直角三角形的重心,且AC=CB,∠ACB=90°,CG=GD,∠CGD=90°,若AC=6cm,则CD= 4cm .
【分析】延长CG交AB于E,由等腰直角三角形的性质及可得到GD∥EB,则,根据G为重心,可得,从而可求CD的长.
【解答】解:延长CG交AB于E,如图所示,
∵△ABC为等腰直角三角形且CE为中线,
∴CE亦为AB上的高,即∠CEB=90°,
又∠CGD=90°,
∴GD∥EB,
∴,
又G为重心,
故,AC=BC=6cm,
∴CD=BC=4cm.
故答案为:4cm.
9.△ABC的面积为6cm2,BC=2cm,则重心G到BC的距离为 2cm .
【分析】根据题意作出图形如右图所示,由三角形面积可得BC边上高AD=6cm,由重心性质可得AG=2GE,过点G作GF⊥BC于点F,再证明△GFE∽△ADE,根据比例式即可求出GF,即重心到BC的距离.
【解答】解:△ABC如图所示,AD为△ABC的高,
∵△ABC的面积为6cm2,BC=2cm,
故AD==6cm.
作BC边上中线AE,
设AE上点G为重心,
由重心的性质可得:AG=2GE,
过点G作GF⊥BC于点F,
∴GF∥AD,
∴△GFE∽△ADE,
∴,
∴GF==2cm,
故重心G到BC的距离为2cm,
故答案为:2cm.
10.如图,四边形ABEG、GEFH、HFCD都是正方形,则∠AFB+∠ACB= 45° .
【分析】由正方形的性质得出∠AEB=45°,AB=BE=EF=FC=a,∠B=90°,EC=2a,由勾股定理求出AE=a,证出 =,再由公共角∠AEF=∠CEA,得出△AEF∽△CEA,得出对应角相等∠AFB=∠EAC,再由三角形的外角性质即可得出结论
【解答】解:∵四边形ABEG、GEFH、HFCD都是边长为a的正方形,
∴∠AEB=45°,AB=BE=EF=FC=a,∠B=90°,
∴EC=2a,AE==a,
∵==,==,
∴=,
又∵∠AEF=∠CEA,
∴△AEF∽△CEA,
∴∠AFB=∠EAC,
∵∠AEB=∠EAC+∠ACB=45°,
∴∠AFB+∠ACB=45°.
故答案为45°.
二.解答题
11.如图,在一个3×5的正方形网格中,△ABC的顶点A,B,C在单位正方形顶点上,请你在图中画一个△A1B1C1,使得△A1B1C1∽△ABC,且点A1,B1,C1都在单位正方形的顶点上.
【分析】首先得出∠ABC=135°,进而利用相似三角形的判定与性质得出可以把这对应边比值看作:2,2:2等,进而得出答案.
【解答】解:由图可知∠ABC=135°,不妨设单位正方形的边长为1个单位,则AB:BC=1:,
由此推断,所画三角形必有一角为135°,且夹该角的两边之比为1:,
也可以把这一比值看作:2,2:2等,以此为突破口,在图连出和2,2和2等线段,
即得△EDF∽△GDH∽△FMN∽△ABC,
如图所示.即图中的△EDF、△GDH、△FMN均可视为△A1B1C1.
12如图,在Rt△ACB中,∠ACB=90°,CD⊥AB,E是斜边AB延长线上一点,∠ECB=∠BCD,AC=4cm,AB=10cm,则BE= .
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】cm
【分析】过B点作BH⊥BC交CE于H,如图,先利用勾股定理计算出BC=2,再利用面积法计算出CD=4,接着计算出BD=2,然后证明△CBH∽△CDB,利用相似比求出BH=,最后证明△EBH∽△EAC,于是利用相似比可求出BE的长.
【解答】解:过B点作BH⊥BC交CE于H,如图,
∵∠ACB=90°,AC=4,AB=10,
∴BC==2,
∵CD⊥AB,
∴CD AB=AC BC,
∴CD==4,
∴BD===2,
∵∠BCH=∠BCD,∠CBH=∠CDB,
∴△CBH∽△CDB,
∴=,即=,解得BH=,
∵BH⊥BC,
∴BH∥AC,
∴△EBH∽△EAC,
∴=,即=,解得EB=(cm).
故答案为cm.
13如图,若,求证:∠ABD=∠ACE.
【考点】相似三角形的判定与性质.
【专题】证明题;推理能力.
【答案】证明见解析部分.
【分析】由可得△ABC∽△ADE,推出∠BAC=∠DAE,推出∠BAD=∠CAE,推出△ABD∽△ACE,再根据相似三角形的性质即可得出答案.
【解答】证明:∵
∴△ABC∽△ADE (三边分别对应成比例的两个三角形相似),
∴∠BAC=∠DAE(相似三角形的对应角相等),
∴∠BAD=∠CAE,
∴△BAD∽△CAE,
∴∠ABD=∠ACE.
14如图所示,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB延长线于F,求证:=.
【考点】相似三角形的判定与性质.
【专题】证明题.
【答案】见试题解答内容
【分析】首先由直角三角形的性质可得:△CBA∽△ABD,根据相似三角形的对应边成比例,可得:AB:AC=BD:AD,又由直角三角形斜边上的中线是斜边的一半,证得:ED=AC=EC,可得:∠C=∠EDC,则易得:∠FAD=∠FDB,∠F为公共角,证得:△DBF∽△ADF,则得:BD:AD=DF:AF,则问题得证.
【解答】证明:∵∠BAC=90°,AD⊥BC,
∴△CBA∽△ABD,
∴=,
∴AB:AC=BD:AD①,
∴∠C=∠FAD,
又∵E为AC的中点,AD⊥BC,
∴ED=AC=EC,
∴∠C=∠EDC,
又∵∠EDC=∠FDB,
∴∠FAD=∠FDB,∠F为公共角,
∴△DBF∽△ADF,
∴BD:AD=DF:AF②,
由①②得,.
15如图:已知△ABC是边长为6的正三角形纸片,沿EF翻折△AEF,使点A落在BC上点A′处,且BA′:A′C=1:2,求:BE和CF的长.
【考点】等边三角形的性质;翻折变换(折叠问题).
【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.
【答案】BE=,CF=.
【分析】由折叠的性质可得AE=A'E,∠A=∠A'=60°,AF=A'F,通过证明△A'BE∽△FCA',可求BE CF=8,在Rt△EHA'中,由勾股定理可求BE的长,即可求解.
【解答】解:过点E作EH⊥BC于H,
∵△ABC是边长为6的等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC=6,
∵BA′:A′C=1:2,
∴BA'=2,A'C=4,
∵沿EF翻折△AEF,
∴AE=A'E,∠A=∠A'=60°,AF=A'F,
∵∠EA'C=∠B+∠A'EB=∠EA'F+∠FA'C,
∴∠BEA'=∠FA'C,
∴△A'BE∽△FCA',
∴,
∴BE CF=2×4=8,
设BE=x,则AE=A'E=6﹣x,
∵∠B=60°,∠BHE=90°,
∴BH=BE=,EH=x,
∴A'H=2﹣,
∵A'E2=EH2+A'H2,
∴(6﹣x)2=(x)2+(2﹣)2,
∴x=,
∴BE=,
∵BE CF=2×4=8,
∴CF=.
16如图,AB是等腰直角三角形ABC的斜边,若点M在边AC上,点N在边BC上,沿直线MN将△MCN翻折,使点C落在边AB上,设其落点为P.
(1)当点P是边AB的中点时,比例式=成立吗?为什么?
(2)当点P不是边AB的中点时,=是否仍然成立?请说明理由.
【考点】等腰直角三角形;相似三角形的判定与性质.
【答案】见试题解答内容
【分析】(1)首先连接PC,易证得△CMN∽△CAB,然后由相似三角形的对应边成比例,证得=1,继而可得比例式=成立;
(2)首先连接PC,则MN⊥PC,过点P作PE⊥AC于点E,易证得△AEP∽△ACB,△MCN∽△PEC,然后由相似三角形的对应边成比例,证得=成立.
【解答】解:(1)点P是边AB的中点时,比例式=成立.
理由:如图(1),连接PC,
∵MN是折痕,
∴MN垂直平分PC,
∵AC=BC,AP=BP,
∴CP⊥AB,=1,
∴MN∥AB,
∴△CMN∽△CAB,
∴=1,
∴=;
(2)当点P不是边AB的中点时,=仍然成立.
理由:如图(2),连接PC,则MN⊥PC,
过点P作PE⊥AC于点E,
∵∠ACB=90°,∠A是公共角,
∴△AEP∽△ACB,
∴,
∵AC=BC,
∴∠A=∠B=45°,∠APE=∠B=45°,
∴AE=EP,
∵∠MCN=90°,CP⊥MN,
∴∠ECP=∠MNC,
∴△MCN∽△PEC,
∴,
∴,
∴=.
17在平面直角坐标系中,已知点A(4,0),点B(0,3).点P从点A出发,以每秒1个单位的速度向右平移,点Q从点B出发,以每秒2个单位的速度向右平移,又P、Q两点同时出发.
(1)连接AQ,当△ABQ是直角三角形时,求点Q的坐标;
(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时∠AQP的度数;
(3)过点A作AC⊥AB,AC交射线PQ于点C,连接BC,D是BC的中点.在点P、Q的运动过程中,是否存在某时刻,使得以A、C、Q、D为顶点的四边形是平行四边形?若存在,试求出这时cot∠ABC的值;若不存在,试说明理由.
【考点】全等三角形的判定与性质;平行四边形的性质;翻折变换(折叠问题);相似三角形的判定与性质.
【答案】见试题解答内容
【分析】(1)由于∠ABQ<90°,若△ABQ是直角三角形,需要考虑两种情况:
①∠BAQ=90°,此时△BAQ∽△ABO,根据相似三角形所得比例线段,可求出BQ的长,即可得到Q点坐标;
②∠BQA=90°,此时四边形BOAQ是矩形,BQ=OA,由此可求出Q点坐标.
(2)假设P点翻折到AB上时,落点为E,那么∠QAP=∠QAE,QE=QP;由于BQ∥OP,那么∠QAP=∠BQA=∠BAQ,即BQ=BA=5,此时P、Q运动了2.5s,所以AP=AE=,即E是AB的中点;分别过E、Q作BQ、OP的垂线,设垂足为F、H,易求EF=PH=,即可证得△QPH≌△QEF,得∠EQF=∠PQH,由此发现∠EQP=90°,而∠PQA=∠EQA,由此可求得∠AQP的度数.
(3)假设存在这样的平行四边形,可分作两种情况考虑:
①点C在线段PQ上,可延长AC、BQ交于点F,由于DQ∥AC,因此DQ是△BCF的中位线,则FC=2DQ=2AC,过F作FH⊥x轴于H,由于∠BAC=90°,可证得△AOB∽△FHA,通过得到的比例线段,即可求出AF的长,进而可得到AC的长;在Rt△BAC中,已知了AC、BA的长,即可求出∠ABC的正切值;
②点C在PQ的延长线上,设AD、AC与BQ的交点分别为G、F,按照①的思路可证得AD=CQ=2AG,那么在相似三角形△CFQ和△AFG中,FC=2AF,即AC=3AF,AF的长在①中已求得,由此可得到AC的长,进而可求出∠ABC的余切值.
【解答】解:(1)根据题意,可得:A(4,0)、B(0,3),AB=5.
ⅰ)当∠BAQ=90°时,△AOB∽△BAQ,
∴BQ:AB=AB:AO.解得 BQ=;
ⅱ)当∠BQA=90°时,BQ=OA=4,
∴Q (,3)或Q(4,3).(4分)
(2)令点P翻折后落在线段AB上的点E处,
则∠EAQ=∠PAQ,∠EQA=∠PQA,AE=AP,QE=QP;
又∵BQ∥OP,
∴∠PAQ=∠BQA,
∴∠EAQ=∠BQA,
即AB=QB=5.
∴AP=BQ=,
∴AE=AP==AB,即点E是AB的中点.
过点E作EF⊥BQ,垂足为点F,过点Q作QH⊥OP,垂足为点H,
则 EF=,PH=,∴EF=PH.
又∵EQ=PQ,∠EFQ=∠PHQ=90°,
∴△EQF≌△PHQ,
∴∠EQF=∠PQH,从而∠PQE=90°.
∴∠AQP=∠AQE=45°.(8分)
(3)当点C在线段PQ上时,延长BQ与AC的延长线交于点F,
∵AC⊥AB,
∴△AOB∽△FHA.
∴AB:FA=AO:FH,即5:FA=4:3,
∴FA=.
∵DQ∥AC,DQ=AC,且D为BC中点,
∴FC=2DQ=2AC.
∴AC=.
在Rt△BAC中,tan∠ABC=;
当点C在PQ的延长线上时,记BQ与AC的交点为F,记AD与BQ的交点为G,
∵CQ∥AD,CQ=AD且D为BC中点,
∴AD=CQ=2DG.
∴CQ=2AG
∵BQ∥OP,AD∥PC,
∴AG=PQ,
∴CQ=2PQ.
∴FC=2AF.
∴AC=.
在Rt△BAC中,tan∠ABC=.
即cot∠ABC==(12分)
一.填空题
1.如图,已知∠ADE=∠ACD=∠ABC,则图中相似三角形共有 对.
2.已知,如图,CD是Rt△ACB斜边上的高,若AD=6,BD=2,CE=3,则BC的长度为 ;BE的长度为 .
3.如图,若AD AB=AE AC,∠A=70°,∠AED=54°,则∠C= 度.
4.如图,已知Rt△ACB中,∠C=90°,四边形MNPQ是正方形,若AN=4,BP=6,则PQ= .
5.已知,如图,AB⊥AC,AC⊥CD,M为线段AC上一动点,AB=4cm,AC=11cm,CD=6cm,当AM= 时,△ABM与以M,C,D构成的三角形相似.
6.如图,Rt△ABC内有三个正方形,DF=9cm,GK=6cm,则PQ的长是 .
7.如图,在△ABC中,D是AB上一点,AE⊥CD,垂足为E,AD=2,DB=1,AC=,且∠ACB=60°,则AE= ;∠ACE= .
8.如图,G是等腰直角三角形的重心,且AC=CB,∠ACB=90°,CG=GD,∠CGD=90°,若AC=6cm,则CD= .
9.△ABC的面积为6cm2,BC=2cm,则重心G到BC的距离为 .
10.如图,四边形ABEG、GEFH、HFCD都是正方形,则∠AFB+∠ACB= .
二.解答题
11.如图,在一个3×5的正方形网格中,△ABC的顶点A,B,C在单位正方形顶点上,请你在图中画一个△A1B1C1,使得△A1B1C1∽△ABC,且点A1,B1,C1都在单位正方形的顶点上.
12如图,在Rt△ACB中,∠ACB=90°,CD⊥AB,E是斜边AB延长线上一点,∠ECB=∠BCD,AC=4cm,AB=10cm,则BE= .
13如图,若,求证:∠ABD=∠ACE.
14如图所示,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB延长线于F,求证:=.
15如图:已知△ABC是边长为6的正三角形纸片,沿EF翻折△AEF,使点A落在BC上点A′处,且BA′:A′C=1:2,求:BE和CF的长.
16如图,AB是等腰直角三角形ABC的斜边,若点M在边AC上,点N在边BC上,沿直线MN将△MCN翻折,使点C落在边AB上,设其落点为P.
(1)当点P是边AB的中点时,比例式=成立吗?为什么?
(2)当点P不是边AB的中点时,=是否仍然成立?请说明理由.
17在平面直角坐标系中,已知点A(4,0),点B(0,3).点P从点A出发,以每秒1个单位的速度向右平移,点Q从点B出发,以每秒2个单位的速度向右平移,又P、Q两点同时出发.
(1)连接AQ,当△ABQ是直角三角形时,求点Q的坐标;
(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时∠AQP的度数;
(3)过点A作AC⊥AB,AC交射线PQ于点C,连接BC,D是BC的中点.在点P、Q的运动过程中,是否存在某时刻,使得以A、C、Q、D为顶点的四边形是平行四边形?若存在,试求出这时cot∠ABC的值;若不存在,试说明理由.
参考答案与试题解析
一.填空题
1.如图,已知∠ADE=∠ACD=∠ABC,则图中相似三角形共有 4 对.
【分析】根据已知先判定线段DE∥BC,再根据相似三角形的判定方法进行分析,从而得到答案.
【解答】解:∵∠ADE=∠ACD=∠ABC,
∴DE∥BC.
∴△ADE∽△ABC,
∵DE∥BC,
∴∠EDC=∠DCB,
∵∠ACD=∠ABC,
∴△EDC∽△DCB,
同理:∠ACD=∠ABC,∠A=∠A,
∴△ABC∽△ACD,
∵△ADE∽△ABC,△ABC∽△ACD,
∴△ADE∽△ACD.
∴共4对.
故答案是:4.
2.已知,如图,CD是Rt△ACB斜边上的高,若AD=6,BD=2,CE=3,则BC的长度为 4 ;BE的长度为 5 .
【分析】根据“CD是Rt△ACB斜边上的高”证得△CDB∽△ACB,进而得到BC2=BD AB,即可求得BC,再利用勾股定理即可得到BE.
【解答】解:∵CD是Rt△ACB斜边上的高,
∴∠CDB=∠ACB=90°,
∵∠DBC=∠CBA,
∴△CDB∽△ACB,
∴=,即BC2=BD AB,
∵AD=6,BD=2,
∴AB=AD+BD=8,
∴BC=4,
在Rt△BCE中,BC=4,CE=3,
∴BE=5.
故答案为:4,5.
3.如图,若AD AB=AE AC,∠A=70°,∠AED=54°,则∠C= 56 度.
【分析】利用相似三角形的判定方法可判断△ADE∽△ACB,则∠ADE=∠C,然后利用三角形内角和计算出∠ADE,从而得到∠C的度数.
【解答】解:∵AD AB=AE AC,
∴=,
而∠DAE=∠CAB,
∴△ADE∽△ACB,
∴∠ADE=∠C,
∵∠ADE=180°﹣∠A﹣∠AED=180°﹣70°﹣54°=56°.
故答案为56.
4.如图,已知Rt△ACB中,∠C=90°,四边形MNPQ是正方形,若AN=4,BP=6,则PQ= 2 .
【分析】设PQ=x,证明△AMN∽△QBP,则利用相似比得到=,即=,然后利用比例性质求出x即可.
【解答】解:设PQ=x,
∵四边形MNPQ是正方形,
∴MN=PQ=x,∠MNP=∠QPN=90°,
∵∠C=90°,
∴∠A+∠B=90°,
而∠A+∠AMN=90°,
∴∠AMN=∠B,
∵∠ANM=∠BPQ,
∴△AMN∽△QBP,
∴=,即=,解得x=2或x=﹣2(舍去),
∴PQ=2.
故答案为2.
5.已知,如图,AB⊥AC,AC⊥CD,M为线段AC上一动点,AB=4cm,AC=11cm,CD=6cm,当AM= cm 时,△ABM与以M,C,D构成的三角形相似.
【分析】首先判定△ABM∽△CDM,然后由该相似三角形的对应边相等得到:=,代入相关数值即可解答.
【解答】解:∵△ABM与以M,C,D构成的三角形相似,且∠AMB=∠CMB,
∴△ABM∽△CDM或△ABM∽△DCM,
如图,∵AB⊥AC,AC⊥CD,
∴AB∥CD.
∴只有△ABM∽△CDM.
∴=.
∵AB=4cm,AC=11cm,CD=6cm,
∴=.
∴AM=(cm).
故答案是:cm.
6.如图,Rt△ABC内有三个正方形,DF=9cm,GK=6cm,则PQ的长是 4cm .
【分析】由相似三角形的判定可得△QPK∽△KGF∽△FDA,由相似三角形的性质可得=,再由正方形的性质可得:PK=KQ﹣QP,GF=DF﹣GK,即可求得PQ的长度.
【解答】解:由已知可得PK∥EF∥AC,
∴△QPK∽△KGF∽△FDA,
∴由相似三角形的性质和正方形的性质可得:=,
又∵PK=KG﹣QP,GF=DF﹣GK,DF=9cm,GK=6cm
∴=,即=,
解得:QP=4.
则PQ的长是4cm;
故答案为:4cm.
7.如图,在△ABC中,D是AB上一点,AE⊥CD,垂足为E,AD=2,DB=1,AC=,且∠ACB=60°,则AE= ;∠ACE= 45° .
【分析】根据“AD=2,DB=1,AC=”得到AC2=AD AB,进而证得△ACD∽△ABC,利用特殊角的锐角三角函数可得AE,再利用勾股定理求得CE,可得AE=CE,即可求得∠ACE.
【解答】解:∵AD=2,DB=1,
∴AB=AD+DB=3,
∵AC=,
∴AC2=AD AB,
∵∠DAC=∠CAB,
∴△ACD∽△ABC,
∴∠ADC=∠ACB=60°,
在Rt△ADE中,AD=2,∠ADC=60°,
∴AE=,
在Rt△ACE中,AE=,AC=,
∴CE=,
∴AE=CE,
∴∠ACE=45°.
故答案为:,45°.
8.如图,G是等腰直角三角形的重心,且AC=CB,∠ACB=90°,CG=GD,∠CGD=90°,若AC=6cm,则CD= 4cm .
【分析】延长CG交AB于E,由等腰直角三角形的性质及可得到GD∥EB,则,根据G为重心,可得,从而可求CD的长.
【解答】解:延长CG交AB于E,如图所示,
∵△ABC为等腰直角三角形且CE为中线,
∴CE亦为AB上的高,即∠CEB=90°,
又∠CGD=90°,
∴GD∥EB,
∴,
又G为重心,
故,AC=BC=6cm,
∴CD=BC=4cm.
故答案为:4cm.
9.△ABC的面积为6cm2,BC=2cm,则重心G到BC的距离为 2cm .
【分析】根据题意作出图形如右图所示,由三角形面积可得BC边上高AD=6cm,由重心性质可得AG=2GE,过点G作GF⊥BC于点F,再证明△GFE∽△ADE,根据比例式即可求出GF,即重心到BC的距离.
【解答】解:△ABC如图所示,AD为△ABC的高,
∵△ABC的面积为6cm2,BC=2cm,
故AD==6cm.
作BC边上中线AE,
设AE上点G为重心,
由重心的性质可得:AG=2GE,
过点G作GF⊥BC于点F,
∴GF∥AD,
∴△GFE∽△ADE,
∴,
∴GF==2cm,
故重心G到BC的距离为2cm,
故答案为:2cm.
10.如图,四边形ABEG、GEFH、HFCD都是正方形,则∠AFB+∠ACB= 45° .
【分析】由正方形的性质得出∠AEB=45°,AB=BE=EF=FC=a,∠B=90°,EC=2a,由勾股定理求出AE=a,证出 =,再由公共角∠AEF=∠CEA,得出△AEF∽△CEA,得出对应角相等∠AFB=∠EAC,再由三角形的外角性质即可得出结论
【解答】解:∵四边形ABEG、GEFH、HFCD都是边长为a的正方形,
∴∠AEB=45°,AB=BE=EF=FC=a,∠B=90°,
∴EC=2a,AE==a,
∵==,==,
∴=,
又∵∠AEF=∠CEA,
∴△AEF∽△CEA,
∴∠AFB=∠EAC,
∵∠AEB=∠EAC+∠ACB=45°,
∴∠AFB+∠ACB=45°.
故答案为45°.
二.解答题
11.如图,在一个3×5的正方形网格中,△ABC的顶点A,B,C在单位正方形顶点上,请你在图中画一个△A1B1C1,使得△A1B1C1∽△ABC,且点A1,B1,C1都在单位正方形的顶点上.
【分析】首先得出∠ABC=135°,进而利用相似三角形的判定与性质得出可以把这对应边比值看作:2,2:2等,进而得出答案.
【解答】解:由图可知∠ABC=135°,不妨设单位正方形的边长为1个单位,则AB:BC=1:,
由此推断,所画三角形必有一角为135°,且夹该角的两边之比为1:,
也可以把这一比值看作:2,2:2等,以此为突破口,在图连出和2,2和2等线段,
即得△EDF∽△GDH∽△FMN∽△ABC,
如图所示.即图中的△EDF、△GDH、△FMN均可视为△A1B1C1.
12如图,在Rt△ACB中,∠ACB=90°,CD⊥AB,E是斜边AB延长线上一点,∠ECB=∠BCD,AC=4cm,AB=10cm,则BE= .
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】cm
【分析】过B点作BH⊥BC交CE于H,如图,先利用勾股定理计算出BC=2,再利用面积法计算出CD=4,接着计算出BD=2,然后证明△CBH∽△CDB,利用相似比求出BH=,最后证明△EBH∽△EAC,于是利用相似比可求出BE的长.
【解答】解:过B点作BH⊥BC交CE于H,如图,
∵∠ACB=90°,AC=4,AB=10,
∴BC==2,
∵CD⊥AB,
∴CD AB=AC BC,
∴CD==4,
∴BD===2,
∵∠BCH=∠BCD,∠CBH=∠CDB,
∴△CBH∽△CDB,
∴=,即=,解得BH=,
∵BH⊥BC,
∴BH∥AC,
∴△EBH∽△EAC,
∴=,即=,解得EB=(cm).
故答案为cm.
13如图,若,求证:∠ABD=∠ACE.
【考点】相似三角形的判定与性质.
【专题】证明题;推理能力.
【答案】证明见解析部分.
【分析】由可得△ABC∽△ADE,推出∠BAC=∠DAE,推出∠BAD=∠CAE,推出△ABD∽△ACE,再根据相似三角形的性质即可得出答案.
【解答】证明:∵
∴△ABC∽△ADE (三边分别对应成比例的两个三角形相似),
∴∠BAC=∠DAE(相似三角形的对应角相等),
∴∠BAD=∠CAE,
∴△BAD∽△CAE,
∴∠ABD=∠ACE.
14如图所示,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB延长线于F,求证:=.
【考点】相似三角形的判定与性质.
【专题】证明题.
【答案】见试题解答内容
【分析】首先由直角三角形的性质可得:△CBA∽△ABD,根据相似三角形的对应边成比例,可得:AB:AC=BD:AD,又由直角三角形斜边上的中线是斜边的一半,证得:ED=AC=EC,可得:∠C=∠EDC,则易得:∠FAD=∠FDB,∠F为公共角,证得:△DBF∽△ADF,则得:BD:AD=DF:AF,则问题得证.
【解答】证明:∵∠BAC=90°,AD⊥BC,
∴△CBA∽△ABD,
∴=,
∴AB:AC=BD:AD①,
∴∠C=∠FAD,
又∵E为AC的中点,AD⊥BC,
∴ED=AC=EC,
∴∠C=∠EDC,
又∵∠EDC=∠FDB,
∴∠FAD=∠FDB,∠F为公共角,
∴△DBF∽△ADF,
∴BD:AD=DF:AF②,
由①②得,.
15如图:已知△ABC是边长为6的正三角形纸片,沿EF翻折△AEF,使点A落在BC上点A′处,且BA′:A′C=1:2,求:BE和CF的长.
【考点】等边三角形的性质;翻折变换(折叠问题).
【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.
【答案】BE=,CF=.
【分析】由折叠的性质可得AE=A'E,∠A=∠A'=60°,AF=A'F,通过证明△A'BE∽△FCA',可求BE CF=8,在Rt△EHA'中,由勾股定理可求BE的长,即可求解.
【解答】解:过点E作EH⊥BC于H,
∵△ABC是边长为6的等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC=6,
∵BA′:A′C=1:2,
∴BA'=2,A'C=4,
∵沿EF翻折△AEF,
∴AE=A'E,∠A=∠A'=60°,AF=A'F,
∵∠EA'C=∠B+∠A'EB=∠EA'F+∠FA'C,
∴∠BEA'=∠FA'C,
∴△A'BE∽△FCA',
∴,
∴BE CF=2×4=8,
设BE=x,则AE=A'E=6﹣x,
∵∠B=60°,∠BHE=90°,
∴BH=BE=,EH=x,
∴A'H=2﹣,
∵A'E2=EH2+A'H2,
∴(6﹣x)2=(x)2+(2﹣)2,
∴x=,
∴BE=,
∵BE CF=2×4=8,
∴CF=.
16如图,AB是等腰直角三角形ABC的斜边,若点M在边AC上,点N在边BC上,沿直线MN将△MCN翻折,使点C落在边AB上,设其落点为P.
(1)当点P是边AB的中点时,比例式=成立吗?为什么?
(2)当点P不是边AB的中点时,=是否仍然成立?请说明理由.
【考点】等腰直角三角形;相似三角形的判定与性质.
【答案】见试题解答内容
【分析】(1)首先连接PC,易证得△CMN∽△CAB,然后由相似三角形的对应边成比例,证得=1,继而可得比例式=成立;
(2)首先连接PC,则MN⊥PC,过点P作PE⊥AC于点E,易证得△AEP∽△ACB,△MCN∽△PEC,然后由相似三角形的对应边成比例,证得=成立.
【解答】解:(1)点P是边AB的中点时,比例式=成立.
理由:如图(1),连接PC,
∵MN是折痕,
∴MN垂直平分PC,
∵AC=BC,AP=BP,
∴CP⊥AB,=1,
∴MN∥AB,
∴△CMN∽△CAB,
∴=1,
∴=;
(2)当点P不是边AB的中点时,=仍然成立.
理由:如图(2),连接PC,则MN⊥PC,
过点P作PE⊥AC于点E,
∵∠ACB=90°,∠A是公共角,
∴△AEP∽△ACB,
∴,
∵AC=BC,
∴∠A=∠B=45°,∠APE=∠B=45°,
∴AE=EP,
∵∠MCN=90°,CP⊥MN,
∴∠ECP=∠MNC,
∴△MCN∽△PEC,
∴,
∴,
∴=.
17在平面直角坐标系中,已知点A(4,0),点B(0,3).点P从点A出发,以每秒1个单位的速度向右平移,点Q从点B出发,以每秒2个单位的速度向右平移,又P、Q两点同时出发.
(1)连接AQ,当△ABQ是直角三角形时,求点Q的坐标;
(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时∠AQP的度数;
(3)过点A作AC⊥AB,AC交射线PQ于点C,连接BC,D是BC的中点.在点P、Q的运动过程中,是否存在某时刻,使得以A、C、Q、D为顶点的四边形是平行四边形?若存在,试求出这时cot∠ABC的值;若不存在,试说明理由.
【考点】全等三角形的判定与性质;平行四边形的性质;翻折变换(折叠问题);相似三角形的判定与性质.
【答案】见试题解答内容
【分析】(1)由于∠ABQ<90°,若△ABQ是直角三角形,需要考虑两种情况:
①∠BAQ=90°,此时△BAQ∽△ABO,根据相似三角形所得比例线段,可求出BQ的长,即可得到Q点坐标;
②∠BQA=90°,此时四边形BOAQ是矩形,BQ=OA,由此可求出Q点坐标.
(2)假设P点翻折到AB上时,落点为E,那么∠QAP=∠QAE,QE=QP;由于BQ∥OP,那么∠QAP=∠BQA=∠BAQ,即BQ=BA=5,此时P、Q运动了2.5s,所以AP=AE=,即E是AB的中点;分别过E、Q作BQ、OP的垂线,设垂足为F、H,易求EF=PH=,即可证得△QPH≌△QEF,得∠EQF=∠PQH,由此发现∠EQP=90°,而∠PQA=∠EQA,由此可求得∠AQP的度数.
(3)假设存在这样的平行四边形,可分作两种情况考虑:
①点C在线段PQ上,可延长AC、BQ交于点F,由于DQ∥AC,因此DQ是△BCF的中位线,则FC=2DQ=2AC,过F作FH⊥x轴于H,由于∠BAC=90°,可证得△AOB∽△FHA,通过得到的比例线段,即可求出AF的长,进而可得到AC的长;在Rt△BAC中,已知了AC、BA的长,即可求出∠ABC的正切值;
②点C在PQ的延长线上,设AD、AC与BQ的交点分别为G、F,按照①的思路可证得AD=CQ=2AG,那么在相似三角形△CFQ和△AFG中,FC=2AF,即AC=3AF,AF的长在①中已求得,由此可得到AC的长,进而可求出∠ABC的余切值.
【解答】解:(1)根据题意,可得:A(4,0)、B(0,3),AB=5.
ⅰ)当∠BAQ=90°时,△AOB∽△BAQ,
∴BQ:AB=AB:AO.解得 BQ=;
ⅱ)当∠BQA=90°时,BQ=OA=4,
∴Q (,3)或Q(4,3).(4分)
(2)令点P翻折后落在线段AB上的点E处,
则∠EAQ=∠PAQ,∠EQA=∠PQA,AE=AP,QE=QP;
又∵BQ∥OP,
∴∠PAQ=∠BQA,
∴∠EAQ=∠BQA,
即AB=QB=5.
∴AP=BQ=,
∴AE=AP==AB,即点E是AB的中点.
过点E作EF⊥BQ,垂足为点F,过点Q作QH⊥OP,垂足为点H,
则 EF=,PH=,∴EF=PH.
又∵EQ=PQ,∠EFQ=∠PHQ=90°,
∴△EQF≌△PHQ,
∴∠EQF=∠PQH,从而∠PQE=90°.
∴∠AQP=∠AQE=45°.(8分)
(3)当点C在线段PQ上时,延长BQ与AC的延长线交于点F,
∵AC⊥AB,
∴△AOB∽△FHA.
∴AB:FA=AO:FH,即5:FA=4:3,
∴FA=.
∵DQ∥AC,DQ=AC,且D为BC中点,
∴FC=2DQ=2AC.
∴AC=.
在Rt△BAC中,tan∠ABC=;
当点C在PQ的延长线上时,记BQ与AC的交点为F,记AD与BQ的交点为G,
∵CQ∥AD,CQ=AD且D为BC中点,
∴AD=CQ=2DG.
∴CQ=2AG
∵BQ∥OP,AD∥PC,
∴AG=PQ,
∴CQ=2PQ.
∴FC=2AF.
∴AC=.
在Rt△BAC中,tan∠ABC=.
即cot∠ABC==(12分)
