第四章 图形的相似 单元测试训练卷 2021-2022学年北师大版数学九年级上册(word版含答案)
文档属性
| 名称 | 第四章 图形的相似 单元测试训练卷 2021-2022学年北师大版数学九年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 164.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 07:46:38 | ||
图片预览



文档简介
北师版九年级数学上册
第四章 图形的相似
单元测试训练卷
一、选择题(共8小题,4*8=32)
1. 下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d=
B.a=4,b=6,c=5,d=10
C.a=2,b=,c=2,d=
D.a=2,b=3,c=4,d=1
2. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,=,则EC的长是( )
A.4.5 B.8 C.10.5 D.14
3. 如图,点D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A.6 B.12 C.18 D.24
4. 如图①,②中各有两个三角形,其边长和角的度数如图上标注,则对图①,②中的两个三角形,下列说法正确的是( )
A.都相似 B.都不相似
C.只有图①相似 D.只有图②相似
5. 如图所示,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A.= B.=
C.∠B=∠D D.∠C=∠AED
6. 在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
7. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )
A.2 B.3 C.2 D.5
8. 如图,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②△ABE∽△AEF;③CF=CD;④S△ABE=4S△ECF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,4*6=24)
9.四条线段a,b,c,d成比例,即=,其中a=3 cm,d=4 cm,c=6 cm,则b等于_______.
10. 已知=,则的值为_______.
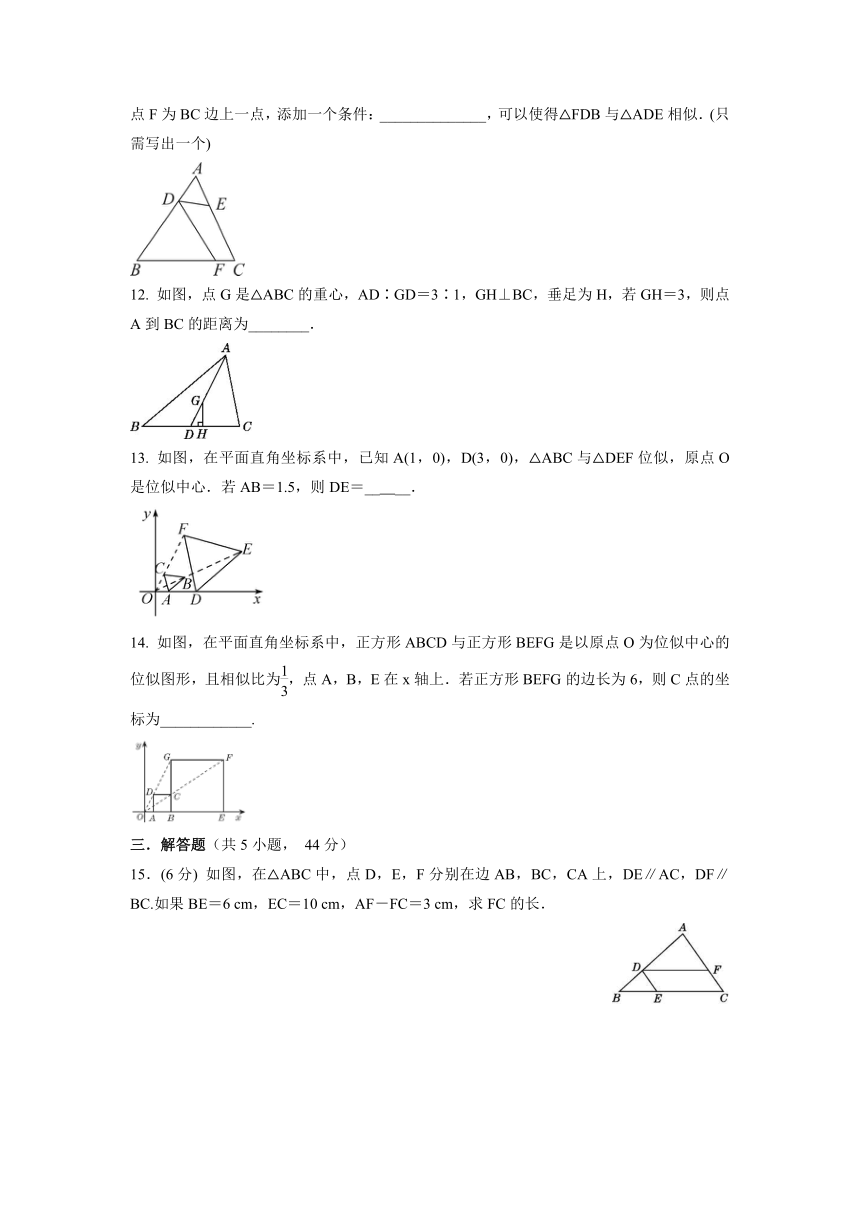
11. 如图,在△ABC中,AB≠AC.D,E分别为边AB,AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:______________,可以使得△FDB与△ADE相似.(只需写出一个)
12. 如图,点G是△ABC的重心,AD∶GD=3∶1,GH⊥BC,垂足为H,若GH=3,则点A到BC的距离为________.
13. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=__ __.
14. 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形BEFG的边长为6,则C点的坐标为____________.
三.解答题(共5小题, 44分)
15.(6分) 如图,在△ABC中,点D,E,F分别在边AB,BC,CA上,DE∥AC,DF∥BC.如果BE=6 cm,EC=10 cm,AF-FC=3 cm,求FC的长.
16.(8分) 如图,矩形ABCD为台球桌面.AD=260 cm,AB=130 cm.球目前在E点位置,AE=60 cm.如果小丁瞄准了BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
17.(8分) 如图,在梯形ABCD中,DC∥AB,AD=BC,E是DC延长线上的点,连接AE,交BC于点F.
(1)求证:△ABF∽△ECF;
(2)如果AD=5 cm,AB=8 cm,CF=2 cm,求CE的长.
18.(10分) 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
19.(12分) 如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长;
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点;
②求λ的值.
参考答案
1-4CBBA 5-8BACB
9.2 cm 10. 11.DF∥AC或∠BFD=∠A 12.9 13. 4.5 14.(3,2)
15. 解:∵DE∥AC,BE=6 cm,EC=10 cm,∴===. 又∵DF∥BC,∴==.∵AF-FC=3 cm,∴=.∴FC=4.5 cm.
16. 解:(1)证明:∵FG⊥BC,∠EFG=∠DFG,∴∠BFE=∠CFD.又∵∠B=∠C=90°,∴△BEF∽△CDF.
(2)设CF=x,则BF=260-x.∵AB=130,AE=60,∴BE=70.由(1)得,△BEF∽△CDF,∴=,即=,∴x=169,即CF=169 cm.
17. (1)证明:∵DC∥AB,∴∠B=∠ECF,∠BAF=∠E,∴△ABF∽△ECF
(2)解:∵AD=BC,AD=5 cm,AB=8 cm,CF=2 cm,∴BF=3 cm.∵由(1)知,△ABF∽△ECF,∴=,即=.∴CE=(cm)
18. (1)∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴∠C+∠B=180°,∠ADF=∠DEC.∵∠AFD+∠AFE=180°,∠AFE=∠B,∴∠AFD=∠C,∴△ADF∽△DEC
(2)∵四边形ABCD是平行四边形,∴CD=AB=8.由(1)知△ADF∽△DEC,∴=,∴DE===12.在Rt△ADE中,由勾股定理得AE===6
19. 解:(1)∵在正方形ABCD中,AD∥BC,∴∠DAG=∠F,又∵AG平分∠DAE,∴∠DAG=∠EAG,∴∠EAG=∠F,∴EA=EF,∵AB=2,∠B=90°,点E为BC的中点,∴BE=EC=1,∴AE==,∴EF=,∴CF=EF-EC=-1
(2)①∵EA=EF,EG⊥AF,∴AG=FG,在△ADG和△FCG中,∴△ADG≌△FCG(AAS),∴DG=CG,即点G为CD的中点
②设CD=2a,则GC=a,由①知,CF=DA=2a,∵EG⊥AF,∠GCF=90°,∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,∴∠EGC=∠F,∴△EGC∽△GFC,∴=,∵GC=a,FC=2a,∴=,∴=,∴EC=a,BE=BC-EC=2a-a=a,∴λ===
第四章 图形的相似
单元测试训练卷
一、选择题(共8小题,4*8=32)
1. 下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d=
B.a=4,b=6,c=5,d=10
C.a=2,b=,c=2,d=
D.a=2,b=3,c=4,d=1
2. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,=,则EC的长是( )
A.4.5 B.8 C.10.5 D.14
3. 如图,点D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A.6 B.12 C.18 D.24
4. 如图①,②中各有两个三角形,其边长和角的度数如图上标注,则对图①,②中的两个三角形,下列说法正确的是( )
A.都相似 B.都不相似
C.只有图①相似 D.只有图②相似
5. 如图所示,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A.= B.=
C.∠B=∠D D.∠C=∠AED
6. 在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
7. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )
A.2 B.3 C.2 D.5
8. 如图,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②△ABE∽△AEF;③CF=CD;④S△ABE=4S△ECF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,4*6=24)
9.四条线段a,b,c,d成比例,即=,其中a=3 cm,d=4 cm,c=6 cm,则b等于_______.
10. 已知=,则的值为_______.
11. 如图,在△ABC中,AB≠AC.D,E分别为边AB,AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:______________,可以使得△FDB与△ADE相似.(只需写出一个)
12. 如图,点G是△ABC的重心,AD∶GD=3∶1,GH⊥BC,垂足为H,若GH=3,则点A到BC的距离为________.
13. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=__ __.
14. 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形BEFG的边长为6,则C点的坐标为____________.
三.解答题(共5小题, 44分)
15.(6分) 如图,在△ABC中,点D,E,F分别在边AB,BC,CA上,DE∥AC,DF∥BC.如果BE=6 cm,EC=10 cm,AF-FC=3 cm,求FC的长.
16.(8分) 如图,矩形ABCD为台球桌面.AD=260 cm,AB=130 cm.球目前在E点位置,AE=60 cm.如果小丁瞄准了BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
17.(8分) 如图,在梯形ABCD中,DC∥AB,AD=BC,E是DC延长线上的点,连接AE,交BC于点F.
(1)求证:△ABF∽△ECF;
(2)如果AD=5 cm,AB=8 cm,CF=2 cm,求CE的长.
18.(10分) 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
19.(12分) 如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长;
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点;
②求λ的值.
参考答案
1-4CBBA 5-8BACB
9.2 cm 10. 11.DF∥AC或∠BFD=∠A 12.9 13. 4.5 14.(3,2)
15. 解:∵DE∥AC,BE=6 cm,EC=10 cm,∴===. 又∵DF∥BC,∴==.∵AF-FC=3 cm,∴=.∴FC=4.5 cm.
16. 解:(1)证明:∵FG⊥BC,∠EFG=∠DFG,∴∠BFE=∠CFD.又∵∠B=∠C=90°,∴△BEF∽△CDF.
(2)设CF=x,则BF=260-x.∵AB=130,AE=60,∴BE=70.由(1)得,△BEF∽△CDF,∴=,即=,∴x=169,即CF=169 cm.
17. (1)证明:∵DC∥AB,∴∠B=∠ECF,∠BAF=∠E,∴△ABF∽△ECF
(2)解:∵AD=BC,AD=5 cm,AB=8 cm,CF=2 cm,∴BF=3 cm.∵由(1)知,△ABF∽△ECF,∴=,即=.∴CE=(cm)
18. (1)∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴∠C+∠B=180°,∠ADF=∠DEC.∵∠AFD+∠AFE=180°,∠AFE=∠B,∴∠AFD=∠C,∴△ADF∽△DEC
(2)∵四边形ABCD是平行四边形,∴CD=AB=8.由(1)知△ADF∽△DEC,∴=,∴DE===12.在Rt△ADE中,由勾股定理得AE===6
19. 解:(1)∵在正方形ABCD中,AD∥BC,∴∠DAG=∠F,又∵AG平分∠DAE,∴∠DAG=∠EAG,∴∠EAG=∠F,∴EA=EF,∵AB=2,∠B=90°,点E为BC的中点,∴BE=EC=1,∴AE==,∴EF=,∴CF=EF-EC=-1
(2)①∵EA=EF,EG⊥AF,∴AG=FG,在△ADG和△FCG中,∴△ADG≌△FCG(AAS),∴DG=CG,即点G为CD的中点
②设CD=2a,则GC=a,由①知,CF=DA=2a,∵EG⊥AF,∠GCF=90°,∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,∴∠EGC=∠F,∴△EGC∽△GFC,∴=,∵GC=a,FC=2a,∴=,∴=,∴EC=a,BE=BC-EC=2a-a=a,∴λ===
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
