2020-2021学年山东省济南市莱芜区大王庄中学六年级(上)月考数学试卷(12月份)(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省济南市莱芜区大王庄中学六年级(上)月考数学试卷(12月份)(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 435.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 11:06:38 | ||
图片预览




文档简介
2020-2021学年山东省济南市莱芜区大王庄中学六年级(上)月考数学试卷(12月份)(五四学制)
一、单选题(共48分)
1.在下列变形中,正确的是( )
A.如果a=b,那么
B.如果,那么a=2
C.如果a﹣b+c=0,那么a=b+c
D.如果a=b,那么a+c=b﹣c
2.若关于x的方程(m﹣2)x|m|﹣1+3=0是一元一次方程,则m值为( )
A.﹣2 B.2 C.﹣3 D.3
3.若是关于x的方程5x﹣m=0的解,则m的值为( )
A.3 B. C.﹣3 D.
4.三棱柱的截面不可能是( )
A.三角形 B.长方形 C.五边形 D.六边形
5.若单项式2x3y2m与﹣3xny2的差仍是单项式,则m+n的值是( )
A.2 B.3 C.4 D.5
6.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是( )
A.这个多项式是五次四项式
B.四次项的系数是7
C.常数项是1
D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+1
7.下列结论中,正确的是( )
A.单项式的系数是3,次数是2
B.﹣xy2z的系数是﹣1,次数是4
C.单项式m的次数是1,没有系数
D.多项式2x2+xy+3是三次三项式
8.若a,b互为相反数,则下面四个等式中一定成立的是( )
A.a+b=0 B.a+b=1 C.|a|+|b|=0 D.|a|+b=0
9.下列说法:①﹣a一定是负数;②|﹣a|一定是正数;③倒数等于它本身的数是±1;④绝对值等于它本身的数是1;⑤平方等于它本身的数是1.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
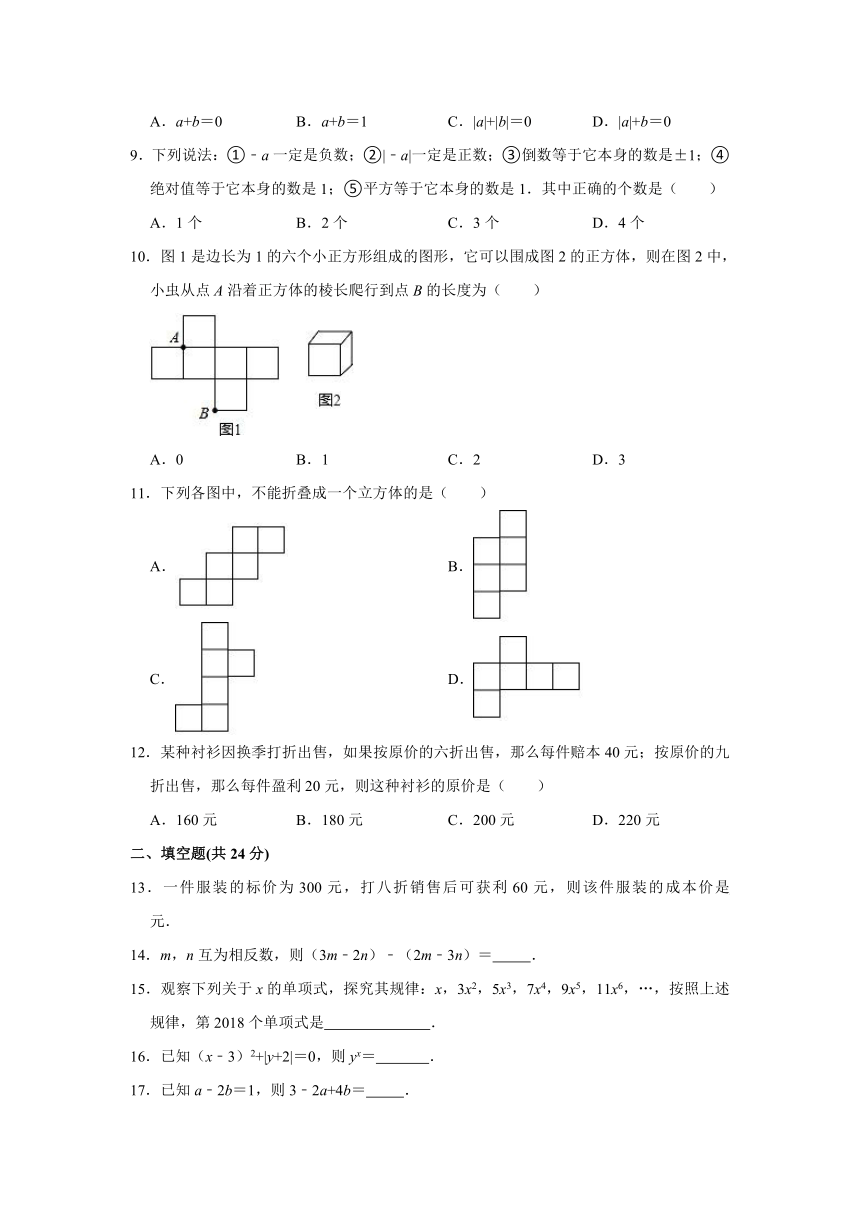
10.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为( )
A.0 B.1 C.2 D.3
11.下列各图中,不能折叠成一个立方体的是( )
A. B.
C. D.
12.某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是( )
A.160元 B.180元 C.200元 D.220元
二、填空题(共24分)
13.一件服装的标价为300元,打八折销售后可获利60元,则该件服装的成本价是 元.
14.m,n互为相反数,则(3m﹣2n)﹣(2m﹣3n)= .
15.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,…,按照上述规律,第2018个单项式是 .
16.已知(x﹣3)2+|y+2|=0,则yx= .
17.已知a﹣2b=1,则3﹣2a+4b= .
18.在数轴上表示a、b两个实数的点的位置如图所示,则化简|a﹣b|﹣|a+b|的结果是 .
三、解答题(共78分)
19.图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
20.′已知a、b互为相反数,c、d互为倒数,m是绝对值等于2的数,求:﹣cd的值.
21.出租车司机李师傅一天下午的营运全是在东西走向的路上进行的,如果规定向东行驶为正,他这天下午行车的里程(单位:千米)如下:+8,+4,﹣10,﹣3,+6,﹣5,﹣2,﹣7,+4,+6
(1)李师傅将第几名乘客送到目的地时,刚好回到下午出发点?
(2)李师傅将最后一名乘客送抵目的地时,他距离出发点多少千米?
(3)如果汽车耗油量为0.3升/千米,那么这天下午汽车共耗油多少升?
22.计算:
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣19)
(2)﹣10﹣8÷(﹣2)×(﹣)
(3)(﹣)×30÷(﹣)
(4)(﹣+﹣)×|﹣12|
(5)18×+13×﹣4×.
(6)(﹣36)÷9.
23.把下列各数表示在数轴上,然后把这些数按从大到小的顺序用“>”连接起来.
0,1,﹣3,﹣(﹣0.5),﹣|﹣|,+(﹣4).
24.解下列一元一次方程:
(1)2﹣3(x+3)=3﹣4(2+x);
(2).
25.化简下列各式:
(1)﹣3x+2y﹣4﹣7y+6
(2)﹣4(3x﹣2y)﹣3(5y﹣2x)
26.某商品每件的标价是280元,按标价的八折销售时,仍可获利12%,则这种商品每件的进价为多少元?
27.公园门票价格规定如下表:
购票张数 1~50张 51~100张 100张以上
每张票的价格 13元 11元 9元
某校七(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)如果两班联合起来,作为一个团体购票,可省多少钱?
(2)两班各有多少学生?
(3)如果七(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
参考答案
一、单选题(共48分)
1.在下列变形中,正确的是( )
A.如果a=b,那么
B.如果,那么a=2
C.如果a﹣b+c=0,那么a=b+c
D.如果a=b,那么a+c=b﹣c
【分析】根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
解:A、两边都乘以3,正确;
B、如果,那么a=8,错误;
C、如果a﹣b+c=0,那么a=b﹣c,错误;
D、如果a=b,那么a﹣c=b﹣c,错误;
故选:A.
2.若关于x的方程(m﹣2)x|m|﹣1+3=0是一元一次方程,则m值为( )
A.﹣2 B.2 C.﹣3 D.3
【分析】只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.它的一般形式是ax+b=0(a,b是常数且a≠0).则x的次数是1且系数不为0,即可得到关于m的方程,即可求解.
解:∵关于x的方程(m﹣2)x|m|﹣1+3=0是一元一次方程,
∴m﹣2≠0且|m|﹣1=1,
解得:m=﹣2,
故选:A.
3.若是关于x的方程5x﹣m=0的解,则m的值为( )
A.3 B. C.﹣3 D.
【分析】把x=代入方程计算即可求出m的值.
解:把x=代入方程得:3﹣m=0,
解得:m=3,
故选:A.
4.三棱柱的截面不可能是( )
A.三角形 B.长方形 C.五边形 D.六边形
【分析】根据截面经过几个面,得到的多边形就是几边形进行判断即可.
解:∵截面与立体图形几个面相交,截面图形就是几边形,而三棱柱有5个面,
∴三棱柱的截面不可能是六边形,
故选:D.
5.若单项式2x3y2m与﹣3xny2的差仍是单项式,则m+n的值是( )
A.2 B.3 C.4 D.5
【分析】根据合并同类项法则得出n=3,2m=2,求出即可.
解:∵单项式2x3y2m与﹣3xny2的差仍是单项式,
∴n=3,2m=2,
解得:m=1,
∴m+n=1+3=4,
故选:C.
6.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是( )
A.这个多项式是五次四项式
B.四次项的系数是7
C.常数项是1
D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+1
【分析】根据多项式的概念即可求出答案.
解:该多项式四次项是﹣7xy3,其系数为﹣7,
故选:B.
7.下列结论中,正确的是( )
A.单项式的系数是3,次数是2
B.﹣xy2z的系数是﹣1,次数是4
C.单项式m的次数是1,没有系数
D.多项式2x2+xy+3是三次三项式
【分析】根据多项式的概念以及系数、次数的定义对各选项分析判断即可得解.
解:A、单项式的系数是,次数是3,故本选项错误不符合题意.
B、﹣xy2z的系数是﹣1,次数是4,本选项正确符合题意.
C、单项式m的次数是1,系数是1,本选项错误不符合题意.
D、多项式2x3+xy+3是二次三项式,故本选项错误不符合题意..
故选:B.
8.若a,b互为相反数,则下面四个等式中一定成立的是( )
A.a+b=0 B.a+b=1 C.|a|+|b|=0 D.|a|+b=0
【分析】此题依据相反数的概念及性质求值.
解:∵a与b互为相反数,
∴a+b=0.
故选:A.
9.下列说法:①﹣a一定是负数;②|﹣a|一定是正数;③倒数等于它本身的数是±1;④绝对值等于它本身的数是1;⑤平方等于它本身的数是1.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据正数和负数的意义,可判断①;
根据绝对值的意义,可判断②;
根据倒数的意义,可判断③;
根据绝对值的性质,可判断④;
根据平方的意义,可判断⑤.
解:①﹣a可能是负数、零、正数,故①说法错误;
②|﹣a|一定是非负数,故②说法错误;
③倒数等于它本身的数是±1,故③说法正确;
④绝对值等于它本身的数是非负数,故④说法错误;
⑤平方等于它本身的数是0或1,故⑤说法错误;
故选:A.
10.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为( )
A.0 B.1 C.2 D.3
【分析】将图1折成正方体,然后判断出A、B在正方体中的位置关系,从而可得到AB之间的距离.
解:将图1折成正方体后点A和点B为同一条棱的两个端点,得出AB=1,
则小虫从点A沿着正方体的棱长爬行到点B的长度为1.
故选:B.
11.下列各图中,不能折叠成一个立方体的是( )
A. B.
C. D.
【分析】由平面图形的折叠及正方体的展开图解题.
解:A、是正方体的展开图,不符合题意;
B、有两个面重合,不是正方体的展开图,符合题意;
C、是正方体的展开图,不符合题意;
D、是正方体的展开图,不符合题意.
故选:B.
12.某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是( )
A.160元 B.180元 C.200元 D.220元
【分析】设这种衬衫的原价是x元,根据衬衫的成本不变,即可得出关于x的一元一次方程,解之即可得出结论.
解:设这种衬衫的原价是x元,
依题意,得:0.6x+40=0.9x﹣20,
解得:x=200.
故选:C.
二、填空题(共24分)
13.一件服装的标价为300元,打八折销售后可获利60元,则该件服装的成本价是 180 元.
【分析】设该件服装的成本价是x元.根据“利润=标价×折扣﹣进价”即可得出关于x的一元一次方程,解方程即可得出结论.
解:设该件服装的成本价是x元,
依题意得:300×﹣x=60,
解得:x=180.
∴该件服装的成本价是180元.
故答案为:180.
14.m,n互为相反数,则(3m﹣2n)﹣(2m﹣3n)= 0 .
【分析】因为m,n互为相反数,所以m+n=0.再对所求代数式进行化简,把m+n的值整体代入即可.
解:依题意得:m+n=0,
∴(3m﹣2n)﹣(2m﹣3n)=m+n=0.
15.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,…,按照上述规律,第2018个单项式是 4035x2018 .
【分析】系数的规律:第n个对应的系数是2n﹣1,指数的规律:第n个对应的指数是n.
解:系数的规律:第n个对应的系数是2n﹣1,指数的规律:第n个对应的指数是n,则第2018个单项式是4035x2018.
故答案为:4035x2018.
16.已知(x﹣3)2+|y+2|=0,则yx= ﹣8 .
【分析】根据非负数的性质求出x、y的值,计算即可.
解:由题意得,x﹣3=0,y+2=0,
解得,x=3,y=﹣2,
则yx=﹣8,
故答案为:﹣8.
17.已知a﹣2b=1,则3﹣2a+4b= 1 .
【分析】先把代数式化为已知的形式,再把已知条件整体代入计算即可.
解:根据题意可得:3﹣2a+4b=3﹣2(a﹣2b)=3﹣2=1.
18.在数轴上表示a、b两个实数的点的位置如图所示,则化简|a﹣b|﹣|a+b|的结果是 2b .
【分析】先根据a、b在数轴上的位置确定出其符号及|a|、|b|的大小,再由绝对值的性质去掉绝对值符号即可.
解:∵由a、b在数轴上的位置可知,a<0,b>0,|a|>|b|,
∴原式=b﹣a+a+b=2b.
故答案为:2b.
三、解答题(共78分)
19.图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
【分析】由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,4,左视图有2列,每列小正方形数目分别为4,3.据此可画出图形.
解:如图所示:
.
20.′已知a、b互为相反数,c、d互为倒数,m是绝对值等于2的数,求:﹣cd的值.
【分析】根据a、b互为相反数,c、d互为倒数,m是绝对值等于2的数,可得:a+b=0,cd=1,m2=4,据此求出+m2﹣cd的值是多少即可.
解:∵a,b互为相反数,
∴a+b=0;
∵c,d互为倒数,
∴cd=1;
∵m的绝对值为2,
∴m2=4;
∴+m2﹣cd
=0+4﹣1
=3
21.出租车司机李师傅一天下午的营运全是在东西走向的路上进行的,如果规定向东行驶为正,他这天下午行车的里程(单位:千米)如下:+8,+4,﹣10,﹣3,+6,﹣5,﹣2,﹣7,+4,+6
(1)李师傅将第几名乘客送到目的地时,刚好回到下午出发点?
(2)李师傅将最后一名乘客送抵目的地时,他距离出发点多少千米?
(3)如果汽车耗油量为0.3升/千米,那么这天下午汽车共耗油多少升?
【分析】(1)根据有理数的加法,可得答案;
(2)根据有理数的加法,可得答案;
(3)根据单位耗油量乘以行驶路程,可得答案.
解:(1)+8+4=12,
12﹣10=2,
2﹣3=﹣1,
﹣1+6=5,
5﹣5=0.
故李师傅将第六名乘客送到目的地时,刚好回到下午出发点;
(2)0﹣2﹣7+4+6=1,
故李师傅将最后一名乘客送抵目的地时,他距离出发点1千米;
(3)(8+4+10+3+6+5+2+7+4+6)×0.3
=55×0.3
=16.5(升).
故这天下午汽车共耗油16.5升.
22.计算:
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣19)
(2)﹣10﹣8÷(﹣2)×(﹣)
(3)(﹣)×30÷(﹣)
(4)(﹣+﹣)×|﹣12|
(5)18×+13×﹣4×.
(6)(﹣36)÷9.
【分析】(1)从左向右依次计算即可.
(2)首先计算除法和乘法,然后计算减法即可.
(3)首先计算小括号里面的运算,然后计算乘法和除法即可.
(4)(5)根据乘法分配律计算即可.
(6)根据除法的性质计算即可.
解:(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣19)
=﹣7﹣11+19
=1
(2)﹣10﹣8÷(﹣2)×(﹣)
=﹣10+4×(﹣)
=﹣10﹣2
=﹣12
(3)(﹣)×30÷(﹣)
=×30÷(﹣)
=5÷(﹣)
=﹣25
(4)(﹣+﹣)×|﹣12|
=(﹣+﹣)×12
=(﹣)×12+×12﹣×12
=﹣6+8﹣3
=﹣1
(5)18×+13×﹣4×
=(18+13﹣4)×
=27×
=18
(6)(﹣36)÷9
=(﹣36﹣)÷9
=(﹣36)÷9﹣÷9
=﹣4﹣
=﹣4
23.把下列各数表示在数轴上,然后把这些数按从大到小的顺序用“>”连接起来.
0,1,﹣3,﹣(﹣0.5),﹣|﹣|,+(﹣4).
【分析】先把各数化简,在数轴上表示出各数,再根据数轴的特点把这些数按从大到小的顺序用“>”连接起来.
解:如图所示:
根据数轴的特点把这些数按从大到小的顺序用“>”连接起来为1>﹣(﹣0.5)>0>﹣|﹣|>﹣3>+(﹣4).
24.解下列一元一次方程:
(1)2﹣3(x+3)=3﹣4(2+x);
(2).
【分析】(1)方程去括号,移项合并,把未知数系数化为1即可;
(2)方程去分母,去括号,移项合并,把未知数系数化为1即可.
解:(1)2﹣3(x+3)=3﹣4(2+x),
去括号,得2﹣3x﹣9=3﹣8﹣4x,
移项,得4x﹣3x=9+3﹣2﹣8,
合并同类项,得x=2;
(2),
去分母,得12﹣(x+5)=6x﹣2(x﹣1),
去括号,得12﹣x﹣5=6x﹣2x+2,
移项,得2x﹣x﹣6x=2+5﹣12,
合并同类项,得﹣5x=﹣5,
系数化为1,得x=1.
25.化简下列各式:
(1)﹣3x+2y﹣4﹣7y+6
(2)﹣4(3x﹣2y)﹣3(5y﹣2x)
【分析】(1)根据合并同类项法则计算可得;
(2)先去括号,再合并同类项即可得.
解:(1)原式=﹣3x+(2﹣7)y+(﹣4+6)=﹣3x﹣5y+2;
(2)原式=﹣12x+8y﹣15y+6x
=﹣6x﹣7y.
26.某商品每件的标价是280元,按标价的八折销售时,仍可获利12%,则这种商品每件的进价为多少元?
【分析】设这种商品每件的进价为x元,根据等量关系:按标价的八折销售时,仍可获利12%,列出关于x的方程,求出方程的解即可得到结果.
解:设这种商品每件的进价为x元,
根据题意得:280×80%﹣x=12%x,
解得:x=200.
答:这种商品每件的进价为200元.
27.公园门票价格规定如下表:
购票张数 1~50张 51~100张 100张以上
每张票的价格 13元 11元 9元
某校七(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)如果两班联合起来,作为一个团体购票,可省多少钱?
(2)两班各有多少学生?
(3)如果七(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
【分析】(1)若设初一(1)班有x人,根据总价钱即可列方程;
(2)利用算术方法即可解答;
(3)应尽量设计的能够享受优惠.
解:(1)1240﹣104×9=304,
∴可省304元钱;
(2)设七(1)班有x人,
则有13x+11(104﹣x)=1240或13x+9(104﹣x)=1240,
解得:x=48或x=76(不合题意,舍去).
即七(1)班48人,七(2)班56人;
(3)要想享受优惠,由(1)可知七(1)班48人,只需多买3张,
51×11=561,48×13=624>561
∴48人买51人的票可以更省钱.
一、单选题(共48分)
1.在下列变形中,正确的是( )
A.如果a=b,那么
B.如果,那么a=2
C.如果a﹣b+c=0,那么a=b+c
D.如果a=b,那么a+c=b﹣c
2.若关于x的方程(m﹣2)x|m|﹣1+3=0是一元一次方程,则m值为( )
A.﹣2 B.2 C.﹣3 D.3
3.若是关于x的方程5x﹣m=0的解,则m的值为( )
A.3 B. C.﹣3 D.
4.三棱柱的截面不可能是( )
A.三角形 B.长方形 C.五边形 D.六边形
5.若单项式2x3y2m与﹣3xny2的差仍是单项式,则m+n的值是( )
A.2 B.3 C.4 D.5
6.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是( )
A.这个多项式是五次四项式
B.四次项的系数是7
C.常数项是1
D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+1
7.下列结论中,正确的是( )
A.单项式的系数是3,次数是2
B.﹣xy2z的系数是﹣1,次数是4
C.单项式m的次数是1,没有系数
D.多项式2x2+xy+3是三次三项式
8.若a,b互为相反数,则下面四个等式中一定成立的是( )
A.a+b=0 B.a+b=1 C.|a|+|b|=0 D.|a|+b=0
9.下列说法:①﹣a一定是负数;②|﹣a|一定是正数;③倒数等于它本身的数是±1;④绝对值等于它本身的数是1;⑤平方等于它本身的数是1.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
10.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为( )
A.0 B.1 C.2 D.3
11.下列各图中,不能折叠成一个立方体的是( )
A. B.
C. D.
12.某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是( )
A.160元 B.180元 C.200元 D.220元
二、填空题(共24分)
13.一件服装的标价为300元,打八折销售后可获利60元,则该件服装的成本价是 元.
14.m,n互为相反数,则(3m﹣2n)﹣(2m﹣3n)= .
15.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,…,按照上述规律,第2018个单项式是 .
16.已知(x﹣3)2+|y+2|=0,则yx= .
17.已知a﹣2b=1,则3﹣2a+4b= .
18.在数轴上表示a、b两个实数的点的位置如图所示,则化简|a﹣b|﹣|a+b|的结果是 .
三、解答题(共78分)
19.图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
20.′已知a、b互为相反数,c、d互为倒数,m是绝对值等于2的数,求:﹣cd的值.
21.出租车司机李师傅一天下午的营运全是在东西走向的路上进行的,如果规定向东行驶为正,他这天下午行车的里程(单位:千米)如下:+8,+4,﹣10,﹣3,+6,﹣5,﹣2,﹣7,+4,+6
(1)李师傅将第几名乘客送到目的地时,刚好回到下午出发点?
(2)李师傅将最后一名乘客送抵目的地时,他距离出发点多少千米?
(3)如果汽车耗油量为0.3升/千米,那么这天下午汽车共耗油多少升?
22.计算:
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣19)
(2)﹣10﹣8÷(﹣2)×(﹣)
(3)(﹣)×30÷(﹣)
(4)(﹣+﹣)×|﹣12|
(5)18×+13×﹣4×.
(6)(﹣36)÷9.
23.把下列各数表示在数轴上,然后把这些数按从大到小的顺序用“>”连接起来.
0,1,﹣3,﹣(﹣0.5),﹣|﹣|,+(﹣4).
24.解下列一元一次方程:
(1)2﹣3(x+3)=3﹣4(2+x);
(2).
25.化简下列各式:
(1)﹣3x+2y﹣4﹣7y+6
(2)﹣4(3x﹣2y)﹣3(5y﹣2x)
26.某商品每件的标价是280元,按标价的八折销售时,仍可获利12%,则这种商品每件的进价为多少元?
27.公园门票价格规定如下表:
购票张数 1~50张 51~100张 100张以上
每张票的价格 13元 11元 9元
某校七(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)如果两班联合起来,作为一个团体购票,可省多少钱?
(2)两班各有多少学生?
(3)如果七(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
参考答案
一、单选题(共48分)
1.在下列变形中,正确的是( )
A.如果a=b,那么
B.如果,那么a=2
C.如果a﹣b+c=0,那么a=b+c
D.如果a=b,那么a+c=b﹣c
【分析】根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
解:A、两边都乘以3,正确;
B、如果,那么a=8,错误;
C、如果a﹣b+c=0,那么a=b﹣c,错误;
D、如果a=b,那么a﹣c=b﹣c,错误;
故选:A.
2.若关于x的方程(m﹣2)x|m|﹣1+3=0是一元一次方程,则m值为( )
A.﹣2 B.2 C.﹣3 D.3
【分析】只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.它的一般形式是ax+b=0(a,b是常数且a≠0).则x的次数是1且系数不为0,即可得到关于m的方程,即可求解.
解:∵关于x的方程(m﹣2)x|m|﹣1+3=0是一元一次方程,
∴m﹣2≠0且|m|﹣1=1,
解得:m=﹣2,
故选:A.
3.若是关于x的方程5x﹣m=0的解,则m的值为( )
A.3 B. C.﹣3 D.
【分析】把x=代入方程计算即可求出m的值.
解:把x=代入方程得:3﹣m=0,
解得:m=3,
故选:A.
4.三棱柱的截面不可能是( )
A.三角形 B.长方形 C.五边形 D.六边形
【分析】根据截面经过几个面,得到的多边形就是几边形进行判断即可.
解:∵截面与立体图形几个面相交,截面图形就是几边形,而三棱柱有5个面,
∴三棱柱的截面不可能是六边形,
故选:D.
5.若单项式2x3y2m与﹣3xny2的差仍是单项式,则m+n的值是( )
A.2 B.3 C.4 D.5
【分析】根据合并同类项法则得出n=3,2m=2,求出即可.
解:∵单项式2x3y2m与﹣3xny2的差仍是单项式,
∴n=3,2m=2,
解得:m=1,
∴m+n=1+3=4,
故选:C.
6.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是( )
A.这个多项式是五次四项式
B.四次项的系数是7
C.常数项是1
D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+1
【分析】根据多项式的概念即可求出答案.
解:该多项式四次项是﹣7xy3,其系数为﹣7,
故选:B.
7.下列结论中,正确的是( )
A.单项式的系数是3,次数是2
B.﹣xy2z的系数是﹣1,次数是4
C.单项式m的次数是1,没有系数
D.多项式2x2+xy+3是三次三项式
【分析】根据多项式的概念以及系数、次数的定义对各选项分析判断即可得解.
解:A、单项式的系数是,次数是3,故本选项错误不符合题意.
B、﹣xy2z的系数是﹣1,次数是4,本选项正确符合题意.
C、单项式m的次数是1,系数是1,本选项错误不符合题意.
D、多项式2x3+xy+3是二次三项式,故本选项错误不符合题意..
故选:B.
8.若a,b互为相反数,则下面四个等式中一定成立的是( )
A.a+b=0 B.a+b=1 C.|a|+|b|=0 D.|a|+b=0
【分析】此题依据相反数的概念及性质求值.
解:∵a与b互为相反数,
∴a+b=0.
故选:A.
9.下列说法:①﹣a一定是负数;②|﹣a|一定是正数;③倒数等于它本身的数是±1;④绝对值等于它本身的数是1;⑤平方等于它本身的数是1.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据正数和负数的意义,可判断①;
根据绝对值的意义,可判断②;
根据倒数的意义,可判断③;
根据绝对值的性质,可判断④;
根据平方的意义,可判断⑤.
解:①﹣a可能是负数、零、正数,故①说法错误;
②|﹣a|一定是非负数,故②说法错误;
③倒数等于它本身的数是±1,故③说法正确;
④绝对值等于它本身的数是非负数,故④说法错误;
⑤平方等于它本身的数是0或1,故⑤说法错误;
故选:A.
10.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为( )
A.0 B.1 C.2 D.3
【分析】将图1折成正方体,然后判断出A、B在正方体中的位置关系,从而可得到AB之间的距离.
解:将图1折成正方体后点A和点B为同一条棱的两个端点,得出AB=1,
则小虫从点A沿着正方体的棱长爬行到点B的长度为1.
故选:B.
11.下列各图中,不能折叠成一个立方体的是( )
A. B.
C. D.
【分析】由平面图形的折叠及正方体的展开图解题.
解:A、是正方体的展开图,不符合题意;
B、有两个面重合,不是正方体的展开图,符合题意;
C、是正方体的展开图,不符合题意;
D、是正方体的展开图,不符合题意.
故选:B.
12.某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是( )
A.160元 B.180元 C.200元 D.220元
【分析】设这种衬衫的原价是x元,根据衬衫的成本不变,即可得出关于x的一元一次方程,解之即可得出结论.
解:设这种衬衫的原价是x元,
依题意,得:0.6x+40=0.9x﹣20,
解得:x=200.
故选:C.
二、填空题(共24分)
13.一件服装的标价为300元,打八折销售后可获利60元,则该件服装的成本价是 180 元.
【分析】设该件服装的成本价是x元.根据“利润=标价×折扣﹣进价”即可得出关于x的一元一次方程,解方程即可得出结论.
解:设该件服装的成本价是x元,
依题意得:300×﹣x=60,
解得:x=180.
∴该件服装的成本价是180元.
故答案为:180.
14.m,n互为相反数,则(3m﹣2n)﹣(2m﹣3n)= 0 .
【分析】因为m,n互为相反数,所以m+n=0.再对所求代数式进行化简,把m+n的值整体代入即可.
解:依题意得:m+n=0,
∴(3m﹣2n)﹣(2m﹣3n)=m+n=0.
15.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,…,按照上述规律,第2018个单项式是 4035x2018 .
【分析】系数的规律:第n个对应的系数是2n﹣1,指数的规律:第n个对应的指数是n.
解:系数的规律:第n个对应的系数是2n﹣1,指数的规律:第n个对应的指数是n,则第2018个单项式是4035x2018.
故答案为:4035x2018.
16.已知(x﹣3)2+|y+2|=0,则yx= ﹣8 .
【分析】根据非负数的性质求出x、y的值,计算即可.
解:由题意得,x﹣3=0,y+2=0,
解得,x=3,y=﹣2,
则yx=﹣8,
故答案为:﹣8.
17.已知a﹣2b=1,则3﹣2a+4b= 1 .
【分析】先把代数式化为已知的形式,再把已知条件整体代入计算即可.
解:根据题意可得:3﹣2a+4b=3﹣2(a﹣2b)=3﹣2=1.
18.在数轴上表示a、b两个实数的点的位置如图所示,则化简|a﹣b|﹣|a+b|的结果是 2b .
【分析】先根据a、b在数轴上的位置确定出其符号及|a|、|b|的大小,再由绝对值的性质去掉绝对值符号即可.
解:∵由a、b在数轴上的位置可知,a<0,b>0,|a|>|b|,
∴原式=b﹣a+a+b=2b.
故答案为:2b.
三、解答题(共78分)
19.图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
【分析】由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,4,左视图有2列,每列小正方形数目分别为4,3.据此可画出图形.
解:如图所示:
.
20.′已知a、b互为相反数,c、d互为倒数,m是绝对值等于2的数,求:﹣cd的值.
【分析】根据a、b互为相反数,c、d互为倒数,m是绝对值等于2的数,可得:a+b=0,cd=1,m2=4,据此求出+m2﹣cd的值是多少即可.
解:∵a,b互为相反数,
∴a+b=0;
∵c,d互为倒数,
∴cd=1;
∵m的绝对值为2,
∴m2=4;
∴+m2﹣cd
=0+4﹣1
=3
21.出租车司机李师傅一天下午的营运全是在东西走向的路上进行的,如果规定向东行驶为正,他这天下午行车的里程(单位:千米)如下:+8,+4,﹣10,﹣3,+6,﹣5,﹣2,﹣7,+4,+6
(1)李师傅将第几名乘客送到目的地时,刚好回到下午出发点?
(2)李师傅将最后一名乘客送抵目的地时,他距离出发点多少千米?
(3)如果汽车耗油量为0.3升/千米,那么这天下午汽车共耗油多少升?
【分析】(1)根据有理数的加法,可得答案;
(2)根据有理数的加法,可得答案;
(3)根据单位耗油量乘以行驶路程,可得答案.
解:(1)+8+4=12,
12﹣10=2,
2﹣3=﹣1,
﹣1+6=5,
5﹣5=0.
故李师傅将第六名乘客送到目的地时,刚好回到下午出发点;
(2)0﹣2﹣7+4+6=1,
故李师傅将最后一名乘客送抵目的地时,他距离出发点1千米;
(3)(8+4+10+3+6+5+2+7+4+6)×0.3
=55×0.3
=16.5(升).
故这天下午汽车共耗油16.5升.
22.计算:
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣19)
(2)﹣10﹣8÷(﹣2)×(﹣)
(3)(﹣)×30÷(﹣)
(4)(﹣+﹣)×|﹣12|
(5)18×+13×﹣4×.
(6)(﹣36)÷9.
【分析】(1)从左向右依次计算即可.
(2)首先计算除法和乘法,然后计算减法即可.
(3)首先计算小括号里面的运算,然后计算乘法和除法即可.
(4)(5)根据乘法分配律计算即可.
(6)根据除法的性质计算即可.
解:(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣19)
=﹣7﹣11+19
=1
(2)﹣10﹣8÷(﹣2)×(﹣)
=﹣10+4×(﹣)
=﹣10﹣2
=﹣12
(3)(﹣)×30÷(﹣)
=×30÷(﹣)
=5÷(﹣)
=﹣25
(4)(﹣+﹣)×|﹣12|
=(﹣+﹣)×12
=(﹣)×12+×12﹣×12
=﹣6+8﹣3
=﹣1
(5)18×+13×﹣4×
=(18+13﹣4)×
=27×
=18
(6)(﹣36)÷9
=(﹣36﹣)÷9
=(﹣36)÷9﹣÷9
=﹣4﹣
=﹣4
23.把下列各数表示在数轴上,然后把这些数按从大到小的顺序用“>”连接起来.
0,1,﹣3,﹣(﹣0.5),﹣|﹣|,+(﹣4).
【分析】先把各数化简,在数轴上表示出各数,再根据数轴的特点把这些数按从大到小的顺序用“>”连接起来.
解:如图所示:
根据数轴的特点把这些数按从大到小的顺序用“>”连接起来为1>﹣(﹣0.5)>0>﹣|﹣|>﹣3>+(﹣4).
24.解下列一元一次方程:
(1)2﹣3(x+3)=3﹣4(2+x);
(2).
【分析】(1)方程去括号,移项合并,把未知数系数化为1即可;
(2)方程去分母,去括号,移项合并,把未知数系数化为1即可.
解:(1)2﹣3(x+3)=3﹣4(2+x),
去括号,得2﹣3x﹣9=3﹣8﹣4x,
移项,得4x﹣3x=9+3﹣2﹣8,
合并同类项,得x=2;
(2),
去分母,得12﹣(x+5)=6x﹣2(x﹣1),
去括号,得12﹣x﹣5=6x﹣2x+2,
移项,得2x﹣x﹣6x=2+5﹣12,
合并同类项,得﹣5x=﹣5,
系数化为1,得x=1.
25.化简下列各式:
(1)﹣3x+2y﹣4﹣7y+6
(2)﹣4(3x﹣2y)﹣3(5y﹣2x)
【分析】(1)根据合并同类项法则计算可得;
(2)先去括号,再合并同类项即可得.
解:(1)原式=﹣3x+(2﹣7)y+(﹣4+6)=﹣3x﹣5y+2;
(2)原式=﹣12x+8y﹣15y+6x
=﹣6x﹣7y.
26.某商品每件的标价是280元,按标价的八折销售时,仍可获利12%,则这种商品每件的进价为多少元?
【分析】设这种商品每件的进价为x元,根据等量关系:按标价的八折销售时,仍可获利12%,列出关于x的方程,求出方程的解即可得到结果.
解:设这种商品每件的进价为x元,
根据题意得:280×80%﹣x=12%x,
解得:x=200.
答:这种商品每件的进价为200元.
27.公园门票价格规定如下表:
购票张数 1~50张 51~100张 100张以上
每张票的价格 13元 11元 9元
某校七(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)如果两班联合起来,作为一个团体购票,可省多少钱?
(2)两班各有多少学生?
(3)如果七(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
【分析】(1)若设初一(1)班有x人,根据总价钱即可列方程;
(2)利用算术方法即可解答;
(3)应尽量设计的能够享受优惠.
解:(1)1240﹣104×9=304,
∴可省304元钱;
(2)设七(1)班有x人,
则有13x+11(104﹣x)=1240或13x+9(104﹣x)=1240,
解得:x=48或x=76(不合题意,舍去).
即七(1)班48人,七(2)班56人;
(3)要想享受优惠,由(1)可知七(1)班48人,只需多买3张,
51×11=561,48×13=624>561
∴48人买51人的票可以更省钱.
同课章节目录
