2021-2022学年度华师版八年级数学上册:14.1 勾股定理(4课时)教案
文档属性
| 名称 | 2021-2022学年度华师版八年级数学上册:14.1 勾股定理(4课时)教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 08:04:34 | ||
图片预览





文档简介
14.1 勾股定理
1 直角三角形三边的关系
第1课时 勾股定理及其证明
一、基本目标
1.会用数格子(或割、补、拼等)的办法体验勾股定理的探索过程、理解勾股定理反映的直角三角形三边之间的数量关系.
2.学会运用勾股定理进行简单的计算和实际运用.
二、重难点目标
【教学重点】
勾股定理的内容.
【教学难点】
勾股定理的探究及证明.
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P108~P111的内容,完成下面练习.
【3 min反馈】
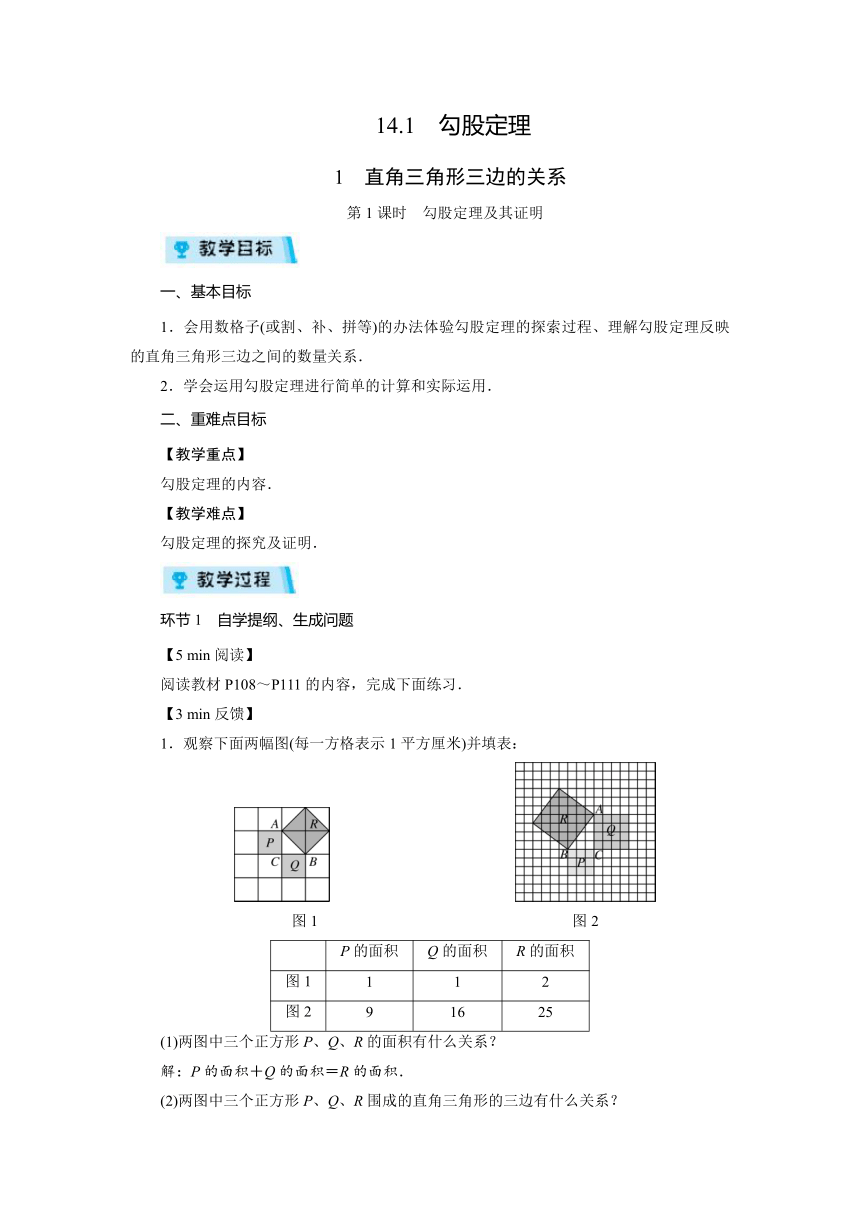
1.观察下面两幅图(每一方格表示1平方厘米)并填表:
图1 图2
P的面积 Q的面积 R的面积
图1 1 1 2
图2 9 16 25
(1)两图中三个正方形P、Q、R的面积有什么关系?
解:P的面积+Q的面积=R的面积.
(2)两图中三个正方形P、Q、R围成的直角三角形的三边有什么关系?
解:AC2+BC2=AB2.
2.勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
3.下列说法中正确的是( C )
A.已知a、b、c是三角形的三边,则a2+b2=c2
B.在直角三角形中,两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,则a2+b2=c2
D.在Rt△ABC中,∠B=90°,则a2+b2=c2
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】作8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再作三个边长分别为a、b、c的正方形,将它们像下图所示拼成两个正方形.
求证:a2+b2=c2.
【互动探索】(引发学生思考)从整体上看,这两个正方形的边长都是a+b,因此它们的面积相等.我们用不同的方法来表示这两个正方形的面积,即可证明勾股定理.
【证明】由图易知,这两个正方形的边长都是a+b,∴它们的面积相等.
左边的正方形面积可表示为a2+b2+ab×4,
右边的正方形面积可表示为c2+ab×4.
∵a2+b2+ab×4=c2+ab×4,
∴a2+b2=c2.
【互动总结】(学生总结,老师点评)根据拼图,通过对拼接图形的面积的不同表示方法,建立相等关系,从而验证勾股定理.
【例2】已知在Rt△ABC中,∠C=90°.
(1)若a=3,b=4,则c2=__,c=__;
(2)若a=6,b=8,则c2=____,c=__;
(3)若c=41,a=9,则b=__;
(4)若c=17,b=8,则a=__.
【互动探索】(引发学生思考)根据勾股定理求解.(1)c2=a2+b2=32+42=25,则c=5.(2) c2=a2+b2=62+82=100,则c=10.(3) 因为c2=a2+b2,所以b===40.(4)因为c2=a2+b2,所以a===15.
【解答】(1)25 5 (2)100 10 (3)40 (4)15
【互动总结】(学生总结,老师点评)本题考查的是勾股定理的应用,如果直角三角形的两条直角边长分别是a、b,斜边长为c,那么a2+b2=c2. a2+b2=c2的常用变形为b=,a=.
活动2 巩固练习(学生独学)
1.在△ABC中,∠C=90°.若 a=5,b=12,则 c=13;若c=41,a=9,则b=40.
2.等腰△ABC的腰长AB=10 cm,底BC为16 cm,则底边上的高为6,面积为48.
3.已知在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=1,b=2,求c;
(2)若a=15,c=17,求b.
解:(1)根据勾股定理,得c2=a2+b2=12+22=5.∵c>0,∴c=.
(2)根据勾股定理,得b2=c2-a2=172-152=64.∵b>0,∴b=8.
活动3 拓展延伸(学生对学)
【例3】在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
【互动探索】应考虑高AD在△ABC内和△ABC外的两种情形.
【解答】当高AD在△ABC内部时,如图1.在Rt△ABD中,由勾股定理,得BD2=AB2-AD2=202-122=162,∴BD=16;在Rt△ACD中,由勾股定理,得CD2=AC2-AD2=152-122=81,∴CD=9.∴BC=BD+CD=25,∴△ABC的周长为25+20+15=60.
当高AD在△ABC外部时,如图2.同理可得BD=16,CD=9.∴BC=BD-CD=7,∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
图1 图2
【互动总结】(学生总结,老师点评)题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
请完成本课时对应练习!
第2课时 勾股定理的简单应用
一、基本目标
理解直角三角形三边的关系,会应用勾股定理解决简单的数学问题.
二、重难点目标
【教学重点】
勾股定理的简单应用.
【教学难点】
勾股定理的简单应用.
环节1自学提纲、生成问题
【5 min阅读】
阅读教材P111~P112的内容,完成下面练习.
【3 min反馈】
1.在△ABC中,∠C=90°.若a=6,c=10,则b=8.
2.某农舍的大门是一个木制的矩形栅栏,它的高为2 m,宽为1.5 m,现需要在相对的顶点间用一块木板加固,木板的长为2.5m.
3.根据下图,利用面积法证明勾股定理.
证明:∵S梯形ABCD=S△ABE+S△DCE+S△EDA,
S梯形ABCD=(a+b)2,S△ABE=S△DCE=ab,S△ADE=c2,∴ (a+b)2=2×ab+c2,
∴a2+b2=c2,即勾股定理得证.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图,已知在△ABC中,∠ACB=90°,AB=5 cm,BC=3 cm,CD⊥AB于点D,求CD的长.
【互动探索】(引发学生思考)要求CD的长,CD是△ABC的高,AB的长已知,如果能求出三角形ABC的面积就好办了.
【解答】∵△ABC是直角三角形,∠ACB=90°,AB=5 cm,BC=3 cm,
∴由勾股定理,得AC2=AB2-BC2=52-32=42,∴AC=4 cm.
又∵S△ABC=AB·CD=AC·BC,
∴CD===(cm).
【互动总结】(学生总结,老师点评)由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,这个规律也称“弦高公式”,它常与勾股定理联合使用.
【例2】我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王算出敌方汽车的速度吗?
【互动探索】(引发学生思考)要求敌方汽车的速度,需要算出BC的长,在Rt△ABC利用勾股定理即可求的BC.
【解答】由勾股定理,得AB2=BC2+AC2,即5002=BC2+4002,所以BC=300 m.
敌方汽车10 s行驶了300 m,那么它1 h行驶的距离为300×6×60=108 000(m),即敌方汽车的速度为108 km/h.
【互动总结】(学生总结,老师点评)用勾股定理解决实际问题的关键是建立直角三角形模型,再代入数据求解.
活动2 巩固练习(学生独学)
1.等腰三角形的腰长为13 cm,底边长为10 cm,则它的面积为( D )
A.30 cm2 B.130 cm2
C.120 cm2 D.60 cm2
2.直角三角形两直角边长分别为5 cm,12 cm,则斜边上的高为cm.
3.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达地点B200 m,结果他在水中实际游了520 m,该河流的宽度为多少?
解:根据图中数据,运用勾股定理,得AB===480(m).
该河流的宽度为480 m.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
勾股定理的简单运用:(1)由直角三角形的任意两边的长度,可以应用勾股定理求出第三边的长度.(2) 用勾股定理解决实际问题的关键是建立直角三角形模型,再代入数据求解.
请完成本课时对应练习!
2 直角三角形的判定(第3课时)
一、基本目标
1.学会用勾股定理逆定理判断三角形是不是直角三角形.
2.理解勾股数的概念,并准确地判断一组数是不是勾股数.
3.能根据直角三角形的判别条件进行一些综合运用.
二、重难点目标
【教学重点】
勾股定理的逆定理,勾股数.
【教学难点】
利用勾股定理的逆定理的应用.
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P112~P114的内容,完成下面练习.
【3 min反馈】
1.下列各组数是一个三角形的三边长.
①a=3,b=4,c=5; ②a=4,b=6,c=8; ③a=6,b=8,c=10.
(1)这三组数都满足a2+b2=c2吗?
(2)分别以每组数为边长作出三角形,看看他们是一些什么样的三角形?
(3)请你说说三角形三边符合什么条件才是直角三角形呢?
请你举出几组勾股数.
解:(1) ①③满足,②不满足.
(2) ①③所画的三角形是直角三角形,②所画的三角形不是直角三角形.
(3)满足a2+b2=c2才是直角三角形.
比如9,40,41;7,24,25;6,8,10等.
2.勾股定理的逆定理:如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形,且边c所对的角为直角.
3.能够成为直接三角形三条边长的三个正整数,称为勾股数.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】判断满足下列条件的三角形是否是直角三角形.
(1)在△ABC中,∠A=20°,∠B=70°;
(2)在△ABC中,AC=7,AB=24,BC=25;
(3)△ABC的三边长a、b、c满足(a+b)(a-b)=c2.
【互动探索】(引发学生思考)分别已知三角形的边和角,如何判定一个三角形是直角三角形呢?
【解答】(1)在△ABC中,∵∠A=20°,∠B=70°,∴∠C=180°-∠A-∠B=90°,即△ABC是直角三角形.
(2)∵AC2+AB2=72+242=625,BC2=252=625,∴AC2+AB2=BC2.根据勾股定理的逆定理可知,△ABC是直角三角形.
(3)∵(a+b)(a-b)=c2,∴a2-b2=c2,即a2=b2+c2.根据勾股定理的逆定理可知,△ABC是直角三角形.
【互动总结】(学生总结,老师点评)判断直角三角形的常用方法有两种:(1)两锐角互余的三角形是直角三角形(即有一个角等于90°的三角形是直角三角形);(2)利用勾股定理的逆定理判断三角形的三边是否满足a2+b2=c2(c为最长边).
【例2】如图,AB=3,CB=4,∠ABC=90°,CD=13,AD=12.求该图形的面积.
【互动探索】(引发学生思考)求不规则图形面积→作辅助线(连结AC)→用S△ADC-S△ACB即可得解.
【解答】连结AC.因为在Rt△ACB中,AB=3,CB=4,所以AC==5.因为在△ACD中,AC2+AD2=52+122=132=DC2,所以△ADC为直角三角形.所以该图形的面积为S△ADC-S△ACB=×5×12-×3×4=24.
【互动总结】(学生总结,老师点评)求解不规则图形面积的常用方法是割补法,即将不规则图形的面积转化为规则图形面积的和或差.
活动2 巩固练习(学生独学)
1.以下列各组数为边长,能组成直角三角形的是( C )
A.5,6,7 B.10,8,4
C.7,25,24 D.9,17,15
2.如果三条线段长a、b、c满足a2=c2-b2,那么这三条线段组成的三角形是不是直角三角形?为什么?
解:是.理由:因为a2=c2-b2,所以a2+b2=c2,由勾股定理的逆定理判断是直角三角形.
3.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a、b、c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
解:对.因为a2+b2=(2m)2+(m2-1)2=4m2+m4-2m2+1=m4+2m2+1=(m2+1)2,而c2=(m2+1)2,所以a2+b2=c2,即a、b、c是勾股数.
m=2时,勾股数为4、3、5;m=3时,勾股数为6、8、10;m=4时,勾股数为8、15、17.
活动3 拓展延伸(学生对学)
【例3】在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
【互动探索】观察图形,猜测AF⊥EF→证明△AEF为直角三角形可得AF⊥EF.
【解答】AF⊥EF.理由:设正方形的边长为4a, 则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,由勾股定理,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,由勾股定理,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,由勾股定理,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,∵AE2=EF2+AF2,∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
【互动总结】(学生总结,老师点评)利用三角形三边的数量关系来判定直角三角形,从而推出两线的垂直关系.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
勾股定理的逆定理:如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形,且边c所对的角为直角.
能够成为直角三角形三条边长的三个正整数,称为勾股数.
请完成本课时对应练习!
3 反证法(第4课时)
一、基本目标
1.通过实例,体会反证法的含义.
2.了解反证法的基本步骤,会用反证法证明简单的命题.
二、重难点目标
【教学重点】
反证法的定义及步骤.
【教学难点】
会用反证法解决问题.
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P114~P117的内容,完成下面练习.
【3 min反馈】
1.列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( B )
A.5 B.2
C.4 D.8
2.间接地去否定与结论相反的一面,从而得出事物真实的一面的证明方法叫做反证法,其步骤为:先假设结论的反面是正确的;然后通过演绎推理,推出与基本事实、已证的定理、定义或已知条件相矛盾;从而说明假设不成立,进而得出原结论正确.
3.用反证法证明:“三角形中最多有一个钝角”时,首先应假设这个三角形中至少有两个角是钝角.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】求证:两直线相交只有一个交点.
已知:两条相交直线l1与l2.
求证:l1与l2只有一个交点.
【教师点拨】分析、证明过程见教材P116例5.
【例2】求证:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC.
求证:△ABC中至少有一个内角小于或等于60°.
【教师点拨】证明过程见教材P116例6.
【例3】如图,在△ABC中,AB=AC,P是△ABC内的一点,且∠APB>∠APC,求证:PB<PC(反证法).
【互动探索】(引发学生思考)假设结论PB<PC不成立,即PB≥PC成立,从假设出发推出与已知相矛盾,得到假设不成立,则结论成立.
【证明】假设PB≥PC.把△ABP绕点A逆时针旋转,使B与C重合,如图:
∵PB≥PC,PB=CD,∴CD≥PC,∴∠CPD≥∠CDP.又∵AP=AD,∴∠APD=∠ADP,∴∠APD+∠CPD≥∠ADP+∠CDP,即∠APC≥∠ADC.又∵∠APB=∠ADC,∴∠APC≥∠APB,与∠APB>∠APC矛盾,∴PB≥PC不成立.综上所述,得PB<PC.
【互动总结】(学生总结,老师点评)用反证法解决问题的关键是找出命题结论的对立面.
活动2 巩固练习(学生独学)
1.用反证法证明:“在一个三角形中,至少有一个内角小于或等于60°”,证明过程大致分3步,第一步是假设在一个三角形中,没有一个内角小于或等于60°.
2.证明:在△ABC中,∠A、∠B、∠C中至少有一个角大于或等于60°.
证明:假设△ABC中每个内角都小于60°,则∠A+∠B+∠C<180°,与三角形内角和定理矛盾,故假设错误,即原结论成立,在△ABC中,∠A、∠B、∠C中至少有一个角大于或等于60°.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
一个命题,当正面证明有困难或者不可能时,就可以尝试用反证法,有时该问题竟能轻易地被解决,此即“正难则反”.
请完成本课时对应练习!
1 直角三角形三边的关系
第1课时 勾股定理及其证明
一、基本目标
1.会用数格子(或割、补、拼等)的办法体验勾股定理的探索过程、理解勾股定理反映的直角三角形三边之间的数量关系.
2.学会运用勾股定理进行简单的计算和实际运用.
二、重难点目标
【教学重点】
勾股定理的内容.
【教学难点】
勾股定理的探究及证明.
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P108~P111的内容,完成下面练习.
【3 min反馈】
1.观察下面两幅图(每一方格表示1平方厘米)并填表:
图1 图2
P的面积 Q的面积 R的面积
图1 1 1 2
图2 9 16 25
(1)两图中三个正方形P、Q、R的面积有什么关系?
解:P的面积+Q的面积=R的面积.
(2)两图中三个正方形P、Q、R围成的直角三角形的三边有什么关系?
解:AC2+BC2=AB2.
2.勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
3.下列说法中正确的是( C )
A.已知a、b、c是三角形的三边,则a2+b2=c2
B.在直角三角形中,两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,则a2+b2=c2
D.在Rt△ABC中,∠B=90°,则a2+b2=c2
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】作8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再作三个边长分别为a、b、c的正方形,将它们像下图所示拼成两个正方形.
求证:a2+b2=c2.
【互动探索】(引发学生思考)从整体上看,这两个正方形的边长都是a+b,因此它们的面积相等.我们用不同的方法来表示这两个正方形的面积,即可证明勾股定理.
【证明】由图易知,这两个正方形的边长都是a+b,∴它们的面积相等.
左边的正方形面积可表示为a2+b2+ab×4,
右边的正方形面积可表示为c2+ab×4.
∵a2+b2+ab×4=c2+ab×4,
∴a2+b2=c2.
【互动总结】(学生总结,老师点评)根据拼图,通过对拼接图形的面积的不同表示方法,建立相等关系,从而验证勾股定理.
【例2】已知在Rt△ABC中,∠C=90°.
(1)若a=3,b=4,则c2=__,c=__;
(2)若a=6,b=8,则c2=____,c=__;
(3)若c=41,a=9,则b=__;
(4)若c=17,b=8,则a=__.
【互动探索】(引发学生思考)根据勾股定理求解.(1)c2=a2+b2=32+42=25,则c=5.(2) c2=a2+b2=62+82=100,则c=10.(3) 因为c2=a2+b2,所以b===40.(4)因为c2=a2+b2,所以a===15.
【解答】(1)25 5 (2)100 10 (3)40 (4)15
【互动总结】(学生总结,老师点评)本题考查的是勾股定理的应用,如果直角三角形的两条直角边长分别是a、b,斜边长为c,那么a2+b2=c2. a2+b2=c2的常用变形为b=,a=.
活动2 巩固练习(学生独学)
1.在△ABC中,∠C=90°.若 a=5,b=12,则 c=13;若c=41,a=9,则b=40.
2.等腰△ABC的腰长AB=10 cm,底BC为16 cm,则底边上的高为6,面积为48.
3.已知在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=1,b=2,求c;
(2)若a=15,c=17,求b.
解:(1)根据勾股定理,得c2=a2+b2=12+22=5.∵c>0,∴c=.
(2)根据勾股定理,得b2=c2-a2=172-152=64.∵b>0,∴b=8.
活动3 拓展延伸(学生对学)
【例3】在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
【互动探索】应考虑高AD在△ABC内和△ABC外的两种情形.
【解答】当高AD在△ABC内部时,如图1.在Rt△ABD中,由勾股定理,得BD2=AB2-AD2=202-122=162,∴BD=16;在Rt△ACD中,由勾股定理,得CD2=AC2-AD2=152-122=81,∴CD=9.∴BC=BD+CD=25,∴△ABC的周长为25+20+15=60.
当高AD在△ABC外部时,如图2.同理可得BD=16,CD=9.∴BC=BD-CD=7,∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
图1 图2
【互动总结】(学生总结,老师点评)题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a、b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
请完成本课时对应练习!
第2课时 勾股定理的简单应用
一、基本目标
理解直角三角形三边的关系,会应用勾股定理解决简单的数学问题.
二、重难点目标
【教学重点】
勾股定理的简单应用.
【教学难点】
勾股定理的简单应用.
环节1自学提纲、生成问题
【5 min阅读】
阅读教材P111~P112的内容,完成下面练习.
【3 min反馈】
1.在△ABC中,∠C=90°.若a=6,c=10,则b=8.
2.某农舍的大门是一个木制的矩形栅栏,它的高为2 m,宽为1.5 m,现需要在相对的顶点间用一块木板加固,木板的长为2.5m.
3.根据下图,利用面积法证明勾股定理.
证明:∵S梯形ABCD=S△ABE+S△DCE+S△EDA,
S梯形ABCD=(a+b)2,S△ABE=S△DCE=ab,S△ADE=c2,∴ (a+b)2=2×ab+c2,
∴a2+b2=c2,即勾股定理得证.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图,已知在△ABC中,∠ACB=90°,AB=5 cm,BC=3 cm,CD⊥AB于点D,求CD的长.
【互动探索】(引发学生思考)要求CD的长,CD是△ABC的高,AB的长已知,如果能求出三角形ABC的面积就好办了.
【解答】∵△ABC是直角三角形,∠ACB=90°,AB=5 cm,BC=3 cm,
∴由勾股定理,得AC2=AB2-BC2=52-32=42,∴AC=4 cm.
又∵S△ABC=AB·CD=AC·BC,
∴CD===(cm).
【互动总结】(学生总结,老师点评)由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,这个规律也称“弦高公式”,它常与勾股定理联合使用.
【例2】我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王算出敌方汽车的速度吗?
【互动探索】(引发学生思考)要求敌方汽车的速度,需要算出BC的长,在Rt△ABC利用勾股定理即可求的BC.
【解答】由勾股定理,得AB2=BC2+AC2,即5002=BC2+4002,所以BC=300 m.
敌方汽车10 s行驶了300 m,那么它1 h行驶的距离为300×6×60=108 000(m),即敌方汽车的速度为108 km/h.
【互动总结】(学生总结,老师点评)用勾股定理解决实际问题的关键是建立直角三角形模型,再代入数据求解.
活动2 巩固练习(学生独学)
1.等腰三角形的腰长为13 cm,底边长为10 cm,则它的面积为( D )
A.30 cm2 B.130 cm2
C.120 cm2 D.60 cm2
2.直角三角形两直角边长分别为5 cm,12 cm,则斜边上的高为cm.
3.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达地点B200 m,结果他在水中实际游了520 m,该河流的宽度为多少?
解:根据图中数据,运用勾股定理,得AB===480(m).
该河流的宽度为480 m.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
勾股定理的简单运用:(1)由直角三角形的任意两边的长度,可以应用勾股定理求出第三边的长度.(2) 用勾股定理解决实际问题的关键是建立直角三角形模型,再代入数据求解.
请完成本课时对应练习!
2 直角三角形的判定(第3课时)
一、基本目标
1.学会用勾股定理逆定理判断三角形是不是直角三角形.
2.理解勾股数的概念,并准确地判断一组数是不是勾股数.
3.能根据直角三角形的判别条件进行一些综合运用.
二、重难点目标
【教学重点】
勾股定理的逆定理,勾股数.
【教学难点】
利用勾股定理的逆定理的应用.
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P112~P114的内容,完成下面练习.
【3 min反馈】
1.下列各组数是一个三角形的三边长.
①a=3,b=4,c=5; ②a=4,b=6,c=8; ③a=6,b=8,c=10.
(1)这三组数都满足a2+b2=c2吗?
(2)分别以每组数为边长作出三角形,看看他们是一些什么样的三角形?
(3)请你说说三角形三边符合什么条件才是直角三角形呢?
请你举出几组勾股数.
解:(1) ①③满足,②不满足.
(2) ①③所画的三角形是直角三角形,②所画的三角形不是直角三角形.
(3)满足a2+b2=c2才是直角三角形.
比如9,40,41;7,24,25;6,8,10等.
2.勾股定理的逆定理:如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形,且边c所对的角为直角.
3.能够成为直接三角形三条边长的三个正整数,称为勾股数.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】判断满足下列条件的三角形是否是直角三角形.
(1)在△ABC中,∠A=20°,∠B=70°;
(2)在△ABC中,AC=7,AB=24,BC=25;
(3)△ABC的三边长a、b、c满足(a+b)(a-b)=c2.
【互动探索】(引发学生思考)分别已知三角形的边和角,如何判定一个三角形是直角三角形呢?
【解答】(1)在△ABC中,∵∠A=20°,∠B=70°,∴∠C=180°-∠A-∠B=90°,即△ABC是直角三角形.
(2)∵AC2+AB2=72+242=625,BC2=252=625,∴AC2+AB2=BC2.根据勾股定理的逆定理可知,△ABC是直角三角形.
(3)∵(a+b)(a-b)=c2,∴a2-b2=c2,即a2=b2+c2.根据勾股定理的逆定理可知,△ABC是直角三角形.
【互动总结】(学生总结,老师点评)判断直角三角形的常用方法有两种:(1)两锐角互余的三角形是直角三角形(即有一个角等于90°的三角形是直角三角形);(2)利用勾股定理的逆定理判断三角形的三边是否满足a2+b2=c2(c为最长边).
【例2】如图,AB=3,CB=4,∠ABC=90°,CD=13,AD=12.求该图形的面积.
【互动探索】(引发学生思考)求不规则图形面积→作辅助线(连结AC)→用S△ADC-S△ACB即可得解.
【解答】连结AC.因为在Rt△ACB中,AB=3,CB=4,所以AC==5.因为在△ACD中,AC2+AD2=52+122=132=DC2,所以△ADC为直角三角形.所以该图形的面积为S△ADC-S△ACB=×5×12-×3×4=24.
【互动总结】(学生总结,老师点评)求解不规则图形面积的常用方法是割补法,即将不规则图形的面积转化为规则图形面积的和或差.
活动2 巩固练习(学生独学)
1.以下列各组数为边长,能组成直角三角形的是( C )
A.5,6,7 B.10,8,4
C.7,25,24 D.9,17,15
2.如果三条线段长a、b、c满足a2=c2-b2,那么这三条线段组成的三角形是不是直角三角形?为什么?
解:是.理由:因为a2=c2-b2,所以a2+b2=c2,由勾股定理的逆定理判断是直角三角形.
3.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a、b、c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
解:对.因为a2+b2=(2m)2+(m2-1)2=4m2+m4-2m2+1=m4+2m2+1=(m2+1)2,而c2=(m2+1)2,所以a2+b2=c2,即a、b、c是勾股数.
m=2时,勾股数为4、3、5;m=3时,勾股数为6、8、10;m=4时,勾股数为8、15、17.
活动3 拓展延伸(学生对学)
【例3】在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
【互动探索】观察图形,猜测AF⊥EF→证明△AEF为直角三角形可得AF⊥EF.
【解答】AF⊥EF.理由:设正方形的边长为4a, 则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,由勾股定理,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,由勾股定理,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,由勾股定理,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,∵AE2=EF2+AF2,∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
【互动总结】(学生总结,老师点评)利用三角形三边的数量关系来判定直角三角形,从而推出两线的垂直关系.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
勾股定理的逆定理:如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形,且边c所对的角为直角.
能够成为直角三角形三条边长的三个正整数,称为勾股数.
请完成本课时对应练习!
3 反证法(第4课时)
一、基本目标
1.通过实例,体会反证法的含义.
2.了解反证法的基本步骤,会用反证法证明简单的命题.
二、重难点目标
【教学重点】
反证法的定义及步骤.
【教学难点】
会用反证法解决问题.
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P114~P117的内容,完成下面练习.
【3 min反馈】
1.列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( B )
A.5 B.2
C.4 D.8
2.间接地去否定与结论相反的一面,从而得出事物真实的一面的证明方法叫做反证法,其步骤为:先假设结论的反面是正确的;然后通过演绎推理,推出与基本事实、已证的定理、定义或已知条件相矛盾;从而说明假设不成立,进而得出原结论正确.
3.用反证法证明:“三角形中最多有一个钝角”时,首先应假设这个三角形中至少有两个角是钝角.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】求证:两直线相交只有一个交点.
已知:两条相交直线l1与l2.
求证:l1与l2只有一个交点.
【教师点拨】分析、证明过程见教材P116例5.
【例2】求证:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC.
求证:△ABC中至少有一个内角小于或等于60°.
【教师点拨】证明过程见教材P116例6.
【例3】如图,在△ABC中,AB=AC,P是△ABC内的一点,且∠APB>∠APC,求证:PB<PC(反证法).
【互动探索】(引发学生思考)假设结论PB<PC不成立,即PB≥PC成立,从假设出发推出与已知相矛盾,得到假设不成立,则结论成立.
【证明】假设PB≥PC.把△ABP绕点A逆时针旋转,使B与C重合,如图:
∵PB≥PC,PB=CD,∴CD≥PC,∴∠CPD≥∠CDP.又∵AP=AD,∴∠APD=∠ADP,∴∠APD+∠CPD≥∠ADP+∠CDP,即∠APC≥∠ADC.又∵∠APB=∠ADC,∴∠APC≥∠APB,与∠APB>∠APC矛盾,∴PB≥PC不成立.综上所述,得PB<PC.
【互动总结】(学生总结,老师点评)用反证法解决问题的关键是找出命题结论的对立面.
活动2 巩固练习(学生独学)
1.用反证法证明:“在一个三角形中,至少有一个内角小于或等于60°”,证明过程大致分3步,第一步是假设在一个三角形中,没有一个内角小于或等于60°.
2.证明:在△ABC中,∠A、∠B、∠C中至少有一个角大于或等于60°.
证明:假设△ABC中每个内角都小于60°,则∠A+∠B+∠C<180°,与三角形内角和定理矛盾,故假设错误,即原结论成立,在△ABC中,∠A、∠B、∠C中至少有一个角大于或等于60°.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
一个命题,当正面证明有困难或者不可能时,就可以尝试用反证法,有时该问题竟能轻易地被解决,此即“正难则反”.
请完成本课时对应练习!
