2021-2022学年度华师版九年级数学上册 25.2随机事件的概率 共3课时(教案)
文档属性
| 名称 | 2021-2022学年度华师版九年级数学上册 25.2随机事件的概率 共3课时(教案) |

|
|
| 格式 | doc | ||
| 文件大小 | 363.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 08:53:52 | ||
图片预览




文档简介
25.2 随机事件的概率
1 概率及其意义(第1课时)
一、基本目标
1.理解概率的意义,并掌握利用概率的意义求一些简单事件概率的方法.
2.经历“猜想——试验——收集数据——分析结果”的探索过程,丰富对随机现象的体验,体会概率是描述不确定现象规律的数学模型.
二、重难点目标
【教学重点】
概率的意义.
【教学难点】
随机事件发生的概率的计算方法.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P136~P141的内容,完成下面练习.
【3 min反馈】
1.一个事件发生的可能性就叫做该事件的__概率__.
2.抛掷一枚正方体骰子,掷得“6”的概率等于,表示如果掷很多很多次的话,那么__平均每6次__有1次掷得“6”.
3.在一个不透明的口袋中,装有10个大小和外形一模一样的小球,其中有6个红球、4个白球,并在口袋中搅匀,任意从口袋中摸出一个球,摸到红球与白球的概率分别是多少?
解:P(摸到红球)==,P(摸到白球)==.即摸到红球与白球的概率分别是,.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】已知一个口袋装有两种只有颜色不同、其他都相同的球,其中3个白球、4个黑球.
(1)求从中随机取出一个黑球的概率;
(2)从中随机取出一个球,取出白球的概率大还是取出黑球的概率大?
(2)若往口袋中再放入x个黑球,且从口袋中随机取出一个白球的概率是,求x的值.
【互动探索】(引发学生思考)要计算事件发生的概率,需要了解概率的意义,利用概率的意义怎样求随机事件发生的概率?
【解答】(1)因为一共有3个白球、4个黑球,
所以从中随机取出一个黑球的概率P==.
(2)P(取出白球)==,P(取出黑球)==.
因为<,
所以取出黑球的概率大.
(3)再放入x个黑球,则一共有(x+7)个球,其中有3个白球,所以从中随机取出一个白球的概率P==,解得x=5.
【互动总结】(学生总结,老师点评)一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)=.
活动2 巩固练习(学生独学)
1.商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”,下列说法正确的是( C )
A.抽10次奖必有1次抽到一等奖
B.抽1次不可能抽到一等奖
C.抽10次也可能没有抽到一等奖
D.抽了9次如果没有抽到一等奖,那么再抽1次肯定抽到一等奖
2.有7张卡片,分别写有1~7这7个数字,将它们背面朝上洗匀后,任意抽出一张.
(1)求抽到数字为偶数的概率;
(2)抽到数字小于5的概率大还是抽到数字大于5的概率大?
解:(1)P(偶数)=.
(2)P(数字小于5)=,P(数字大于5)=.因为>,所以抽到数字小于5的概率大.
3.某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成20个扇形,如图)并规定:顾客在本商场每消费200元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券,某顾客消费210元.
(1)他转动转盘获得购物券的概率是多少?
(2)他得到100元、50元、20元购物券的概率分别是多少?
解:(1)P(获得购物券)=.
(2)P(获得100元)=,P(获得50元)==,P(获得20元)==.
活动3 拓展延伸(学生对学)
【例2】随意抛一粒豆子,恰好落在如图所示的圆内,那么这粒豆子落在正方形里面的概率大还是落在正方形外面的概率大?
【互动探索】要计算随机事件A发生的概率,得知道在一次试验中,可能结果的总数和事件A包含的结果数,那么在平面图形中,应该怎么计算随机事件发生的概率?
【解答】设圆的半径为1,则正方形的边长为.
圆的面积为πr2=π,正方形的面积为()2=2.
故这粒豆子落在正方形里面的概率为,落在正方形外面的概率为.
因为>,
所以这粒豆子落在正方形里面的概率大.
【互动总结】(学生总结,老师点评)有关平面图形中随机事件发生的概率,可以根据图形面积来计算,随机事件发生对应的图形面积与图形总面积的比值就是随机事件发生的概率.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
概率
请完成本课时对应练习!
2 频率与概率(第2课时)
一、基本目标
1.理解用随机事件的频率估计事件发生的概率的正确性.
2.掌握用随机事件的频率估计事件发生的概率的方法.
二、重难点目标
【教学重点】
用频率估计概率的条件与方法.
【教学难点】
由试验得出的频率与理论分析得出的概率之间的关系.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P141~P146的内容,完成下面练习.
【3 min反馈】
1.抛掷一枚质地均匀的硬币时,“出现两正”“出现两反”“出现一正一反”“出现一反一正”的可能性__相等__,这四个随机事件发生的概率都是____.通过试验可以发现:在重复抛掷一枚硬币时,“出现两正”“出现两反”“出现一正一反”“出现一反一正”的频率的稳定值在____左右.由此可知,理论分析与重复试验得到的结论是__一致__的.
2.通过重复试验用频率估计概率,必须要求试验是在__相同条件__下进行的,试验次数越__多__,就越有可能得到较好的__估计__值,但不同小组试验所得的估计值也并不一定相同.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】一颗木质的中国象棋子“车”,正面雕刻一个“车”字,它的反面是平的,将它从一定高度掷下,落地反弹后可能是“车”字面朝上,也可能是“车”字面朝下,由于棋子的两面不均匀,为了估计“车”字面朝上的概率,九年级某实验小组做了掷棋子的试验,试验数据如下表:
试验次数 20 80 100 160 200 240 300 360 400
“车”字朝上的频数 14 48 50 84 112 144 172 204 228
相应的频率 0.70 0.60 0.53 0.56 0.60 0.57
(1)请将数据表补充完整;
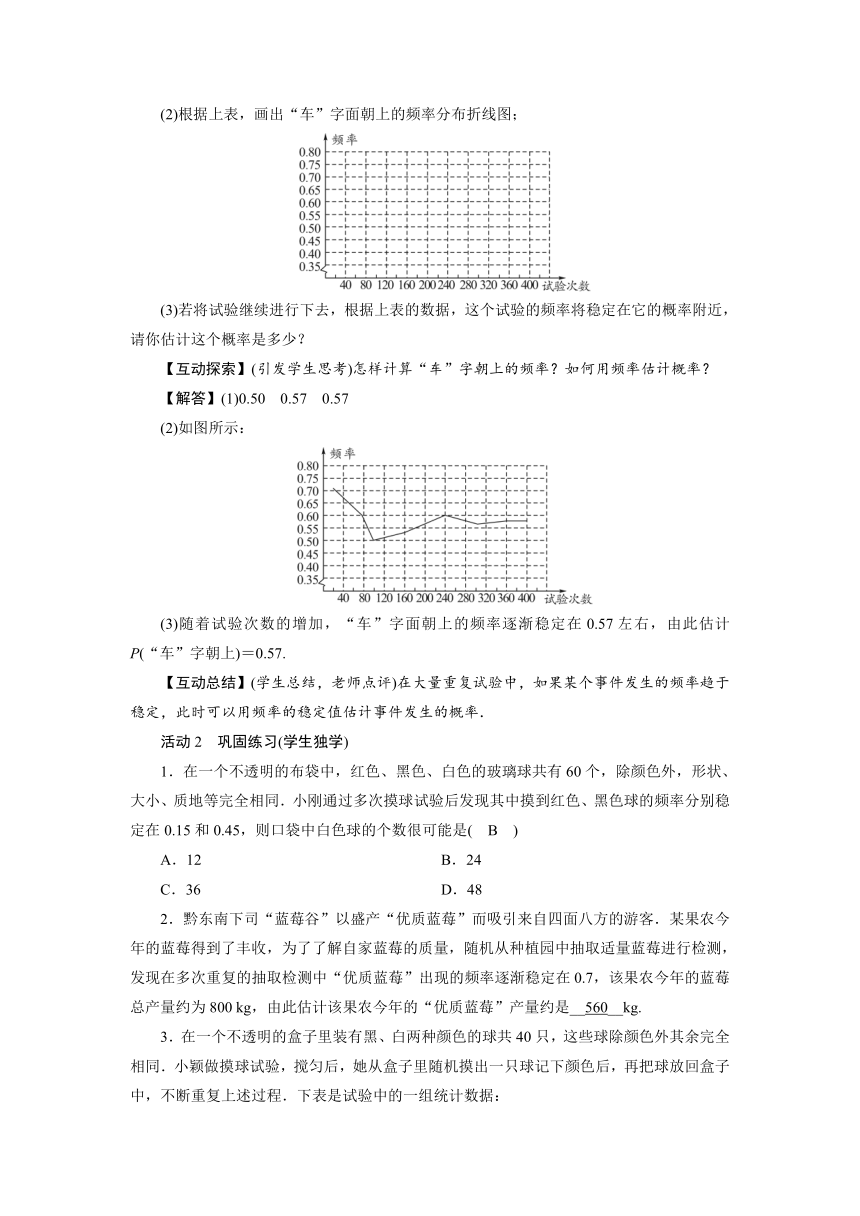
(2)根据上表,画出“车”字面朝上的频率分布折线图;
(3)若将试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少?
【互动探索】(引发学生思考)怎样计算“车”字朝上的频率?如何用频率估计概率?
【解答】(1)0.50 0.57 0.57
(2)如图所示:
(3)随着试验次数的增加,“车”字面朝上的频率逐渐稳定在0.57左右,由此估计P(“车”字朝上)=0.57.
【互动总结】(学生总结,老师点评)在大量重复试验中,如果某个事件发生的频率趋于稳定,此时可以用频率的稳定值估计事件发生的概率.
活动2 巩固练习(学生独学)
1.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在0.15和0.45,则口袋中白色球的个数很可能是( B )
A.12 B.24
C.36 D.48
2.黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客.某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800 kg,由此估计该果农今年的“优质蓝莓”产量约是__560__kg.
3.在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程.下表是试验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 65 124 178 302 481 599 1803
摸到白球的频率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
(1)当n很大时,摸到白球的频率将会接近 __0.6__;(精确到0.1)
(2)若从盒子里随机摸出一只球,则摸到白球的概率的估计值为__0.6__;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
解:40×0.6=24(个),40-24=16(个),故盒子里黑、白两种颜色的球各有16个、24个.
活动3 拓展延伸(学生对学)
【例2】在一个不透明的盒子里装有颜色不同的黑、白两种球共60个,它们除颜色不同外,其余都相同,王颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率定于0.25.
(1)请估计摸到白球的概率将会接近____________;
(2)计算盒子里白、黑两种颜色的球各有多少个?
(3)如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?
【互动探索】频率和概率之间有什么关系?怎么求简单随机事件的概率?
【解答】(1)0.25
(2)60×0.25=15(个),60-15=45(个),故盒子里白、黑两种颜色的球各有15个、45个.
(3)设需要往盒子里再放入x个白球.
根据题意,得=,解得x=15.
故需要往盒子里再放入15个白球.
【互动总结】(学生总结,老师点评)利用频率估计概率,所用频率必须是大量重复试验的稳定值.根据概率的定义求随机事件的概率时,注意事件包含的结果总数.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
生活中的随机事件事件发生的频率事件发生的概率实际生活中的事件
请完成本课时对应练习!
3 列举所有机会均等的结果(第3课时)
一、基本目标
1.掌握用画树状图法和列表法求简单事件的概率.
2.理解在什么条件下使用列表法,在什么条件下使用画树状图法.
二、重难点目标
【教学重点】
利用画树状图法和列表法求随机事件的概率.
【教学难点】
选择合适的方法列举事件的所有等可能的结果.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P149~P152的内容,完成下面练习.
【3 min反馈】
1.在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小__相等__,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率.
2.教材P150上方[思考]答案为__不同意__这种说法.理由:用画树状图法可得:“全是正面”的概率为 ____,“两正一反”的概率为____,“两反一正”的概率为____,“全是反面”的概率为____.
3.教材P150下方[思考]答案为他的分析__没有__道理.理由:每次从口袋中摸出红球和摸出白球的概率__不相等__.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】同时抛掷3枚质地相同的硬币,求下列事件的概率.
(1)三枚硬币的正面都朝上;
(2)有两枚硬币的正面朝上;
(3)至少有两枚硬币的正面朝上.
【互动探索】(引发学生思考)要求随机事件发生的概率,就要知道所有的结果数,题中涉及三枚硬币,用什么方法来列举所有结果比较方便?
【解答】画树状图如下:
由树状图可知,一共有8种等可能结果,即(上,上,上),(上,上,下),(上,下,上),(上,下,下),(下,上,上),(下,上,下),(下,下,上),(下,下,下).
(1)三枚硬币的正面都朝上的结果有1种,即(上,上,上),所以P(三枚硬币的正面都朝上)=.
(2)有两枚硬币的正面朝上的结果有3种,即(上,上,下),(上,下,上),(下,上,上),所以P(有两枚硬币的正面朝上)=.
(3)至少有两枚硬币的正面朝上的结果有4种,即(上,上,下),(上,下,上),(下,上,上),(上,上,上),所以P(至少有两枚硬币的正面朝上)==.
【互动总结】(学生总结,老师点评)当一次试验涉及三个或更多个因素时,用画树状图法列举出所有可能性相同的结果,再利用概率公式P=计算事件的概率.
【例2】有5张看上去无差别的卡片,正面分别写着1,2,3,4,5,洗匀后正面向下放在桌面上,从中随机抽取1张,记下数字后放回洗匀,再从中随机抽取1张.
(1)求两次抽到的数都是偶数的概率;
(2)求第一次抽到的数比第二次抽到的数大的概率;
(3)求两次抽到的数相等的概率.
【互动探索】(引发学生思考)问题中抽取卡片的结果数比较多,应该怎么列举出所有可能的结果?
【解答】列表如下:
第一次第二次 1 2 3 4 5
1 (1,1) (2,1) (3,1) (4,1) (5,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5)
由表可以看出,可能出现的结果一共有25种,并且它们出现的可能性相等.
(1)两次抽到的数都是偶数的结果有4种,即(2,2),(2,4),(4,2),(4,4),所以P(两次抽到的数都是偶数)=.
(2)第一次抽到的数比第二次抽到的数大的结果有10种,即(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),所以P(第一次抽到的数比第二次抽到的数大)==.
(3)两次抽到的数相等的结果有5种,即(1,1),(2,2),(3,3),(4,4),(5,5),所以P(两次抽到的数相等)==.
【互动总结】(学生总结,老师点评)在一次试验中,如果可能出现的结果比较多,且各种结果出现的可能性大小相等,那么我们可以列表列举出试验结果,从而求出随机事件发生的概率.
活动2 巩固练习(学生独学)
1.在一个不透明的袋中装有2个黄球和2个红球,它们除颜色外没有其他区别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸出一个球,那么两次都摸到黄球的概率是( C )
A. B.
C. D.
2.李玲有红色、黄色、白色的三件运动短袖上衣和白色、黄色两条运动短裤,若任意组合穿着,则李玲穿着“衣裤同色”的概率是____.
3.小明、小亮、小红三人参加课外兴趣小组,他们都计划从航模小组、科技小组、美术小组中选择一个.
(1)求三人选择同一个兴趣小组的概率;
(2)求三人都选择不同兴趣小组的概率.
解:(1)P(三人选择同一个兴趣小组)=.
(2)P(三人都选择不同兴趣小组)=.
4.同时掷两枚质地均匀的六面体骰子,计算下列事件的概率:
(1)两枚骰子点数的和是6;
(2)两枚骰子点数都大于4;
(3)其中一枚骰子的点数是3.
解:(1)P(两枚骰子点数的和是6)=.
(2)P(两枚骰子点数都大于4)==.
(3)P(其中一枚骰子的点数是3)=.
活动3 拓展延伸(学生对学)
【例3】如图所示,小明和小亮用转盘做“配紫色”游戏(红色和蓝色在一起能配成紫色),小明转动的A盘被等分成4个扇形,小亮转动的B盘被等分成3个扇形,两人分别转动转盘一次.两人转动转盘得到的两种颜色若能配成紫色则小明获胜,否则小亮获胜,这个游戏对双方公平吗?如果不公平,应该怎么修改游戏规则才对双方公平?
转盘A 转盘B
【互动探索】结合概率的相关知识,要使游戏对双方公平,则两人获胜的概率之间有什么关系?
【解答】列表如下:
红 蓝 黄
蓝 (红,蓝) (蓝,蓝) (黄,蓝)
红 (红,红) (蓝,红) (黄,红)
黄 (红,黄) (蓝,黄) (黄,黄)
红 (红,红) (蓝,红) (黄,红)
由表可知,两人分别转动转盘一次,可能出现的结果共有12种,并且它们出现的可能性相同.
其中能配成紫色的结果有3种,所以P(小明获胜)==,P(小亮获胜)=1-=.
因为<,
所以这个游戏对双方不公平.
要使游戏对双方公平,可以改为能配成紫色小明获胜,两个转盘的颜色相同,则小亮获胜.
【互动总结】(学生总结,老师点评)判断一个游戏对双方是否公平,就看双方获胜的概率是否相等,若相等,则公平,否则不公平.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
随机事件的概率P(A)=
请完成本课时对应练习!
1 概率及其意义(第1课时)
一、基本目标
1.理解概率的意义,并掌握利用概率的意义求一些简单事件概率的方法.
2.经历“猜想——试验——收集数据——分析结果”的探索过程,丰富对随机现象的体验,体会概率是描述不确定现象规律的数学模型.
二、重难点目标
【教学重点】
概率的意义.
【教学难点】
随机事件发生的概率的计算方法.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P136~P141的内容,完成下面练习.
【3 min反馈】
1.一个事件发生的可能性就叫做该事件的__概率__.
2.抛掷一枚正方体骰子,掷得“6”的概率等于,表示如果掷很多很多次的话,那么__平均每6次__有1次掷得“6”.
3.在一个不透明的口袋中,装有10个大小和外形一模一样的小球,其中有6个红球、4个白球,并在口袋中搅匀,任意从口袋中摸出一个球,摸到红球与白球的概率分别是多少?
解:P(摸到红球)==,P(摸到白球)==.即摸到红球与白球的概率分别是,.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】已知一个口袋装有两种只有颜色不同、其他都相同的球,其中3个白球、4个黑球.
(1)求从中随机取出一个黑球的概率;
(2)从中随机取出一个球,取出白球的概率大还是取出黑球的概率大?
(2)若往口袋中再放入x个黑球,且从口袋中随机取出一个白球的概率是,求x的值.
【互动探索】(引发学生思考)要计算事件发生的概率,需要了解概率的意义,利用概率的意义怎样求随机事件发生的概率?
【解答】(1)因为一共有3个白球、4个黑球,
所以从中随机取出一个黑球的概率P==.
(2)P(取出白球)==,P(取出黑球)==.
因为<,
所以取出黑球的概率大.
(3)再放入x个黑球,则一共有(x+7)个球,其中有3个白球,所以从中随机取出一个白球的概率P==,解得x=5.
【互动总结】(学生总结,老师点评)一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)=.
活动2 巩固练习(学生独学)
1.商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”,下列说法正确的是( C )
A.抽10次奖必有1次抽到一等奖
B.抽1次不可能抽到一等奖
C.抽10次也可能没有抽到一等奖
D.抽了9次如果没有抽到一等奖,那么再抽1次肯定抽到一等奖
2.有7张卡片,分别写有1~7这7个数字,将它们背面朝上洗匀后,任意抽出一张.
(1)求抽到数字为偶数的概率;
(2)抽到数字小于5的概率大还是抽到数字大于5的概率大?
解:(1)P(偶数)=.
(2)P(数字小于5)=,P(数字大于5)=.因为>,所以抽到数字小于5的概率大.
3.某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成20个扇形,如图)并规定:顾客在本商场每消费200元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券,某顾客消费210元.
(1)他转动转盘获得购物券的概率是多少?
(2)他得到100元、50元、20元购物券的概率分别是多少?
解:(1)P(获得购物券)=.
(2)P(获得100元)=,P(获得50元)==,P(获得20元)==.
活动3 拓展延伸(学生对学)
【例2】随意抛一粒豆子,恰好落在如图所示的圆内,那么这粒豆子落在正方形里面的概率大还是落在正方形外面的概率大?
【互动探索】要计算随机事件A发生的概率,得知道在一次试验中,可能结果的总数和事件A包含的结果数,那么在平面图形中,应该怎么计算随机事件发生的概率?
【解答】设圆的半径为1,则正方形的边长为.
圆的面积为πr2=π,正方形的面积为()2=2.
故这粒豆子落在正方形里面的概率为,落在正方形外面的概率为.
因为>,
所以这粒豆子落在正方形里面的概率大.
【互动总结】(学生总结,老师点评)有关平面图形中随机事件发生的概率,可以根据图形面积来计算,随机事件发生对应的图形面积与图形总面积的比值就是随机事件发生的概率.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
概率
请完成本课时对应练习!
2 频率与概率(第2课时)
一、基本目标
1.理解用随机事件的频率估计事件发生的概率的正确性.
2.掌握用随机事件的频率估计事件发生的概率的方法.
二、重难点目标
【教学重点】
用频率估计概率的条件与方法.
【教学难点】
由试验得出的频率与理论分析得出的概率之间的关系.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P141~P146的内容,完成下面练习.
【3 min反馈】
1.抛掷一枚质地均匀的硬币时,“出现两正”“出现两反”“出现一正一反”“出现一反一正”的可能性__相等__,这四个随机事件发生的概率都是____.通过试验可以发现:在重复抛掷一枚硬币时,“出现两正”“出现两反”“出现一正一反”“出现一反一正”的频率的稳定值在____左右.由此可知,理论分析与重复试验得到的结论是__一致__的.
2.通过重复试验用频率估计概率,必须要求试验是在__相同条件__下进行的,试验次数越__多__,就越有可能得到较好的__估计__值,但不同小组试验所得的估计值也并不一定相同.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】一颗木质的中国象棋子“车”,正面雕刻一个“车”字,它的反面是平的,将它从一定高度掷下,落地反弹后可能是“车”字面朝上,也可能是“车”字面朝下,由于棋子的两面不均匀,为了估计“车”字面朝上的概率,九年级某实验小组做了掷棋子的试验,试验数据如下表:
试验次数 20 80 100 160 200 240 300 360 400
“车”字朝上的频数 14 48 50 84 112 144 172 204 228
相应的频率 0.70 0.60 0.53 0.56 0.60 0.57
(1)请将数据表补充完整;
(2)根据上表,画出“车”字面朝上的频率分布折线图;
(3)若将试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少?
【互动探索】(引发学生思考)怎样计算“车”字朝上的频率?如何用频率估计概率?
【解答】(1)0.50 0.57 0.57
(2)如图所示:
(3)随着试验次数的增加,“车”字面朝上的频率逐渐稳定在0.57左右,由此估计P(“车”字朝上)=0.57.
【互动总结】(学生总结,老师点评)在大量重复试验中,如果某个事件发生的频率趋于稳定,此时可以用频率的稳定值估计事件发生的概率.
活动2 巩固练习(学生独学)
1.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在0.15和0.45,则口袋中白色球的个数很可能是( B )
A.12 B.24
C.36 D.48
2.黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客.某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800 kg,由此估计该果农今年的“优质蓝莓”产量约是__560__kg.
3.在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程.下表是试验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 65 124 178 302 481 599 1803
摸到白球的频率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
(1)当n很大时,摸到白球的频率将会接近 __0.6__;(精确到0.1)
(2)若从盒子里随机摸出一只球,则摸到白球的概率的估计值为__0.6__;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
解:40×0.6=24(个),40-24=16(个),故盒子里黑、白两种颜色的球各有16个、24个.
活动3 拓展延伸(学生对学)
【例2】在一个不透明的盒子里装有颜色不同的黑、白两种球共60个,它们除颜色不同外,其余都相同,王颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率定于0.25.
(1)请估计摸到白球的概率将会接近____________;
(2)计算盒子里白、黑两种颜色的球各有多少个?
(3)如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?
【互动探索】频率和概率之间有什么关系?怎么求简单随机事件的概率?
【解答】(1)0.25
(2)60×0.25=15(个),60-15=45(个),故盒子里白、黑两种颜色的球各有15个、45个.
(3)设需要往盒子里再放入x个白球.
根据题意,得=,解得x=15.
故需要往盒子里再放入15个白球.
【互动总结】(学生总结,老师点评)利用频率估计概率,所用频率必须是大量重复试验的稳定值.根据概率的定义求随机事件的概率时,注意事件包含的结果总数.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
生活中的随机事件事件发生的频率事件发生的概率实际生活中的事件
请完成本课时对应练习!
3 列举所有机会均等的结果(第3课时)
一、基本目标
1.掌握用画树状图法和列表法求简单事件的概率.
2.理解在什么条件下使用列表法,在什么条件下使用画树状图法.
二、重难点目标
【教学重点】
利用画树状图法和列表法求随机事件的概率.
【教学难点】
选择合适的方法列举事件的所有等可能的结果.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P149~P152的内容,完成下面练习.
【3 min反馈】
1.在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小__相等__,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率.
2.教材P150上方[思考]答案为__不同意__这种说法.理由:用画树状图法可得:“全是正面”的概率为 ____,“两正一反”的概率为____,“两反一正”的概率为____,“全是反面”的概率为____.
3.教材P150下方[思考]答案为他的分析__没有__道理.理由:每次从口袋中摸出红球和摸出白球的概率__不相等__.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】同时抛掷3枚质地相同的硬币,求下列事件的概率.
(1)三枚硬币的正面都朝上;
(2)有两枚硬币的正面朝上;
(3)至少有两枚硬币的正面朝上.
【互动探索】(引发学生思考)要求随机事件发生的概率,就要知道所有的结果数,题中涉及三枚硬币,用什么方法来列举所有结果比较方便?
【解答】画树状图如下:
由树状图可知,一共有8种等可能结果,即(上,上,上),(上,上,下),(上,下,上),(上,下,下),(下,上,上),(下,上,下),(下,下,上),(下,下,下).
(1)三枚硬币的正面都朝上的结果有1种,即(上,上,上),所以P(三枚硬币的正面都朝上)=.
(2)有两枚硬币的正面朝上的结果有3种,即(上,上,下),(上,下,上),(下,上,上),所以P(有两枚硬币的正面朝上)=.
(3)至少有两枚硬币的正面朝上的结果有4种,即(上,上,下),(上,下,上),(下,上,上),(上,上,上),所以P(至少有两枚硬币的正面朝上)==.
【互动总结】(学生总结,老师点评)当一次试验涉及三个或更多个因素时,用画树状图法列举出所有可能性相同的结果,再利用概率公式P=计算事件的概率.
【例2】有5张看上去无差别的卡片,正面分别写着1,2,3,4,5,洗匀后正面向下放在桌面上,从中随机抽取1张,记下数字后放回洗匀,再从中随机抽取1张.
(1)求两次抽到的数都是偶数的概率;
(2)求第一次抽到的数比第二次抽到的数大的概率;
(3)求两次抽到的数相等的概率.
【互动探索】(引发学生思考)问题中抽取卡片的结果数比较多,应该怎么列举出所有可能的结果?
【解答】列表如下:
第一次第二次 1 2 3 4 5
1 (1,1) (2,1) (3,1) (4,1) (5,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5)
由表可以看出,可能出现的结果一共有25种,并且它们出现的可能性相等.
(1)两次抽到的数都是偶数的结果有4种,即(2,2),(2,4),(4,2),(4,4),所以P(两次抽到的数都是偶数)=.
(2)第一次抽到的数比第二次抽到的数大的结果有10种,即(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),所以P(第一次抽到的数比第二次抽到的数大)==.
(3)两次抽到的数相等的结果有5种,即(1,1),(2,2),(3,3),(4,4),(5,5),所以P(两次抽到的数相等)==.
【互动总结】(学生总结,老师点评)在一次试验中,如果可能出现的结果比较多,且各种结果出现的可能性大小相等,那么我们可以列表列举出试验结果,从而求出随机事件发生的概率.
活动2 巩固练习(学生独学)
1.在一个不透明的袋中装有2个黄球和2个红球,它们除颜色外没有其他区别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸出一个球,那么两次都摸到黄球的概率是( C )
A. B.
C. D.
2.李玲有红色、黄色、白色的三件运动短袖上衣和白色、黄色两条运动短裤,若任意组合穿着,则李玲穿着“衣裤同色”的概率是____.
3.小明、小亮、小红三人参加课外兴趣小组,他们都计划从航模小组、科技小组、美术小组中选择一个.
(1)求三人选择同一个兴趣小组的概率;
(2)求三人都选择不同兴趣小组的概率.
解:(1)P(三人选择同一个兴趣小组)=.
(2)P(三人都选择不同兴趣小组)=.
4.同时掷两枚质地均匀的六面体骰子,计算下列事件的概率:
(1)两枚骰子点数的和是6;
(2)两枚骰子点数都大于4;
(3)其中一枚骰子的点数是3.
解:(1)P(两枚骰子点数的和是6)=.
(2)P(两枚骰子点数都大于4)==.
(3)P(其中一枚骰子的点数是3)=.
活动3 拓展延伸(学生对学)
【例3】如图所示,小明和小亮用转盘做“配紫色”游戏(红色和蓝色在一起能配成紫色),小明转动的A盘被等分成4个扇形,小亮转动的B盘被等分成3个扇形,两人分别转动转盘一次.两人转动转盘得到的两种颜色若能配成紫色则小明获胜,否则小亮获胜,这个游戏对双方公平吗?如果不公平,应该怎么修改游戏规则才对双方公平?
转盘A 转盘B
【互动探索】结合概率的相关知识,要使游戏对双方公平,则两人获胜的概率之间有什么关系?
【解答】列表如下:
红 蓝 黄
蓝 (红,蓝) (蓝,蓝) (黄,蓝)
红 (红,红) (蓝,红) (黄,红)
黄 (红,黄) (蓝,黄) (黄,黄)
红 (红,红) (蓝,红) (黄,红)
由表可知,两人分别转动转盘一次,可能出现的结果共有12种,并且它们出现的可能性相同.
其中能配成紫色的结果有3种,所以P(小明获胜)==,P(小亮获胜)=1-=.
因为<,
所以这个游戏对双方不公平.
要使游戏对双方公平,可以改为能配成紫色小明获胜,两个转盘的颜色相同,则小亮获胜.
【互动总结】(学生总结,老师点评)判断一个游戏对双方是否公平,就看双方获胜的概率是否相等,若相等,则公平,否则不公平.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
随机事件的概率P(A)=
请完成本课时对应练习!
