浙江省十校联合体2013届高三上学期期初联考数学(文)试题
文档属性
| 名称 | 浙江省十校联合体2013届高三上学期期初联考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 172.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-10 21:21:26 | ||
图片预览



文档简介
十校联合体2013届高三上学期期初联考数学(文)试题
(完卷时间:120分钟, 满分:150分,本次考试不得使用计算器)
一.选择题:本大题共10题,每小题5分,共50分.
1.设集合≤x≤2},B=,则= ( )
A.[1,2] B.[0,2] C. [1,4] D.[0,4]
2.设(是虚数单位),则= ( )
A. B. C. D.
3. 已知{an}是等比数列,,则公比q= ( )
A. B.-2 C.2 D.
4.设变量满足约束条件,则目标函数的最大值为 ( )
A.-3 B.2 C.4 D.5
5.将圆平分的直线的方程可以是 ( )
A. B. C. D.
6.若正数满足,则 的最大值是 ( )
A. B. C.2 D.
A为三角形的内角,则的 ( )
A.充分不必要条件 B.必要不充分条件 C. 充要条件D.既不充分也不必要条件
8.已知抛物线的焦点与椭圆的一个焦点重合,
它们在第一象限内的交点为,且与轴垂直,则椭圆的离心率为 ( )
A. B. C. D.
9.若恒成立,其中 ( )
A. B. C. D.
以下四个命题
(1) 在△ABC中,内角A,B,C的对边分别为a,b,c,且,则
(2)设是两个非零向量且,则存在实数λ,使得;
(3)方程在实数范围内的解有且仅有一个;
(4);
其中正确的个数有 ( )
A.1个 B. 2个 C. 3 D.4个
二.填空题:本大题共7小题,每小题4分,共28分
11.f (x)为偶函数且 则f (-1)=
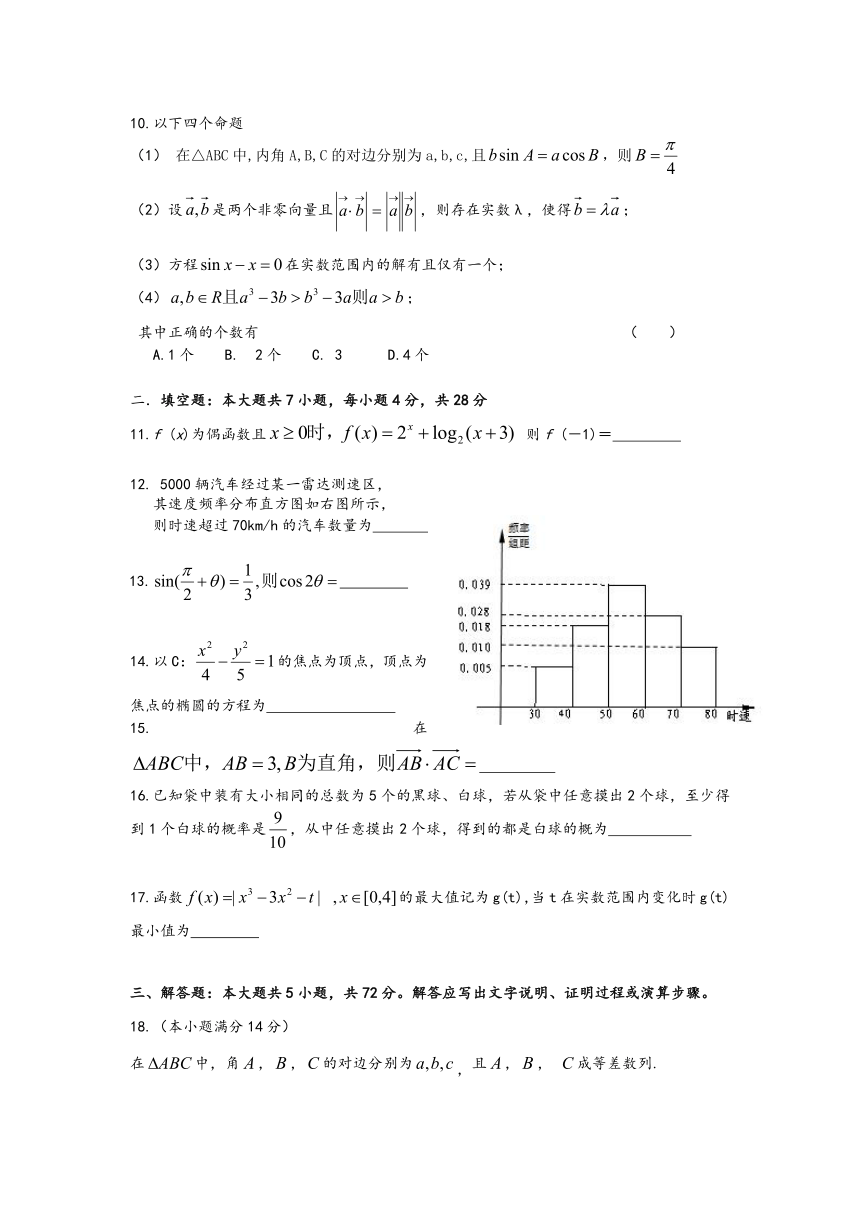
12. 5000辆汽车经过某一雷达测速区,
其速度频率分布直方图如右图所示,
则时速超过70km/h的汽车数量为
13.
14.以C:的焦点为顶点,顶点为焦点的椭圆的方程为
15.在
已知袋中装有大小相同的总数为5个的黑球、白球,若从袋中任意摸出2个球,至少得到1个白球的概率是,从中任意摸出2个球,得到的都是白球的概为
17.函数 的最大值记为g(t),当t在实数范围内变化时g(t)最小值为
解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.(本小题满分14分)
在中,角,,的对边分别为,且,, 成等差数列.
(1)若,求的值;(2)求sinA+sinC的最大值.
19.(本小题满分14分)
已知在递增等差数列中, ,成等比数列数列的前n项和为Sn,且.21世纪教育网
(1)求数列、的通项公式;(2)设,求数列的前和.
(本小题满分14分)
若,求;
若函数对应的图象记为
(I)求曲线在处的切线方程?(II)若直线为曲线的切线,并且直线与曲线有且仅有一个公共点,求所有这样直线的方程?
(本小题满分15分)
已知函数.
(1)求的单调区间;(2)设,若对任意,均存在,使得,求的取值范围.
(本小题满分15分)
已知P为曲线C上任一点,若P到点F的距离与P到直线距离相等
(1)求曲线C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点A、B,
(I)若,求直线l的方程;(II)试问在x轴上是否存在定点E(a,0),使 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
2012学年第一学期温州十校联合体高三期中联考
数学(文科)答案
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项
中,只有一项是符合题目要求的。
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
(2)解:由已知sinA+sinC=sinA+sin(-B-A)=sinA+sin(-B)………………………10
=sinA+cosA+sinA………………12
=sin(A+)≤.………13 当△ABC为正三角形时取等号。………………14
(本小题满分14分)
21.(本小题满分15分)
解:(1), ………………2分
①当时,由于,故, ………………3分
所以,的单调递增区间为 ( http: / / www. ). ………………4分
②当时,由,得. ………………5分
在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.
………………7分
(2)由已知,转化为 ( http: / / www. ). ………………8分
………………9分
由(1)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.) ………………11分
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,, ………14分
所以,解得. ………15分
(完卷时间:120分钟, 满分:150分,本次考试不得使用计算器)
一.选择题:本大题共10题,每小题5分,共50分.
1.设集合≤x≤2},B=,则= ( )
A.[1,2] B.[0,2] C. [1,4] D.[0,4]
2.设(是虚数单位),则= ( )
A. B. C. D.
3. 已知{an}是等比数列,,则公比q= ( )
A. B.-2 C.2 D.
4.设变量满足约束条件,则目标函数的最大值为 ( )
A.-3 B.2 C.4 D.5
5.将圆平分的直线的方程可以是 ( )
A. B. C. D.
6.若正数满足,则 的最大值是 ( )
A. B. C.2 D.
A为三角形的内角,则的 ( )
A.充分不必要条件 B.必要不充分条件 C. 充要条件D.既不充分也不必要条件
8.已知抛物线的焦点与椭圆的一个焦点重合,
它们在第一象限内的交点为,且与轴垂直,则椭圆的离心率为 ( )
A. B. C. D.
9.若恒成立,其中 ( )
A. B. C. D.
以下四个命题
(1) 在△ABC中,内角A,B,C的对边分别为a,b,c,且,则
(2)设是两个非零向量且,则存在实数λ,使得;
(3)方程在实数范围内的解有且仅有一个;
(4);
其中正确的个数有 ( )
A.1个 B. 2个 C. 3 D.4个
二.填空题:本大题共7小题,每小题4分,共28分
11.f (x)为偶函数且 则f (-1)=
12. 5000辆汽车经过某一雷达测速区,
其速度频率分布直方图如右图所示,
则时速超过70km/h的汽车数量为
13.
14.以C:的焦点为顶点,顶点为焦点的椭圆的方程为
15.在
已知袋中装有大小相同的总数为5个的黑球、白球,若从袋中任意摸出2个球,至少得到1个白球的概率是,从中任意摸出2个球,得到的都是白球的概为
17.函数 的最大值记为g(t),当t在实数范围内变化时g(t)最小值为
解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.(本小题满分14分)
在中,角,,的对边分别为,且,, 成等差数列.
(1)若,求的值;(2)求sinA+sinC的最大值.
19.(本小题满分14分)
已知在递增等差数列中, ,成等比数列数列的前n项和为Sn,且.21世纪教育网
(1)求数列、的通项公式;(2)设,求数列的前和.
(本小题满分14分)
若,求;
若函数对应的图象记为
(I)求曲线在处的切线方程?(II)若直线为曲线的切线,并且直线与曲线有且仅有一个公共点,求所有这样直线的方程?
(本小题满分15分)
已知函数.
(1)求的单调区间;(2)设,若对任意,均存在,使得,求的取值范围.
(本小题满分15分)
已知P为曲线C上任一点,若P到点F的距离与P到直线距离相等
(1)求曲线C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点A、B,
(I)若,求直线l的方程;(II)试问在x轴上是否存在定点E(a,0),使 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
2012学年第一学期温州十校联合体高三期中联考
数学(文科)答案
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项
中,只有一项是符合题目要求的。
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
(2)解:由已知sinA+sinC=sinA+sin(-B-A)=sinA+sin(-B)………………………10
=sinA+cosA+sinA………………12
=sin(A+)≤.………13 当△ABC为正三角形时取等号。………………14
(本小题满分14分)
21.(本小题满分15分)
解:(1), ………………2分
①当时,由于,故, ………………3分
所以,的单调递增区间为 ( http: / / www. ). ………………4分
②当时,由,得. ………………5分
在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.
………………7分
(2)由已知,转化为 ( http: / / www. ). ………………8分
………………9分
由(1)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.) ………………11分
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,, ………14分
所以,解得. ………15分
同课章节目录
