2021-2022学年沪科新版九年级上册数学《第22章 相似形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪科新版九年级上册数学《第22章 相似形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 350.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 12:31:17 | ||
图片预览

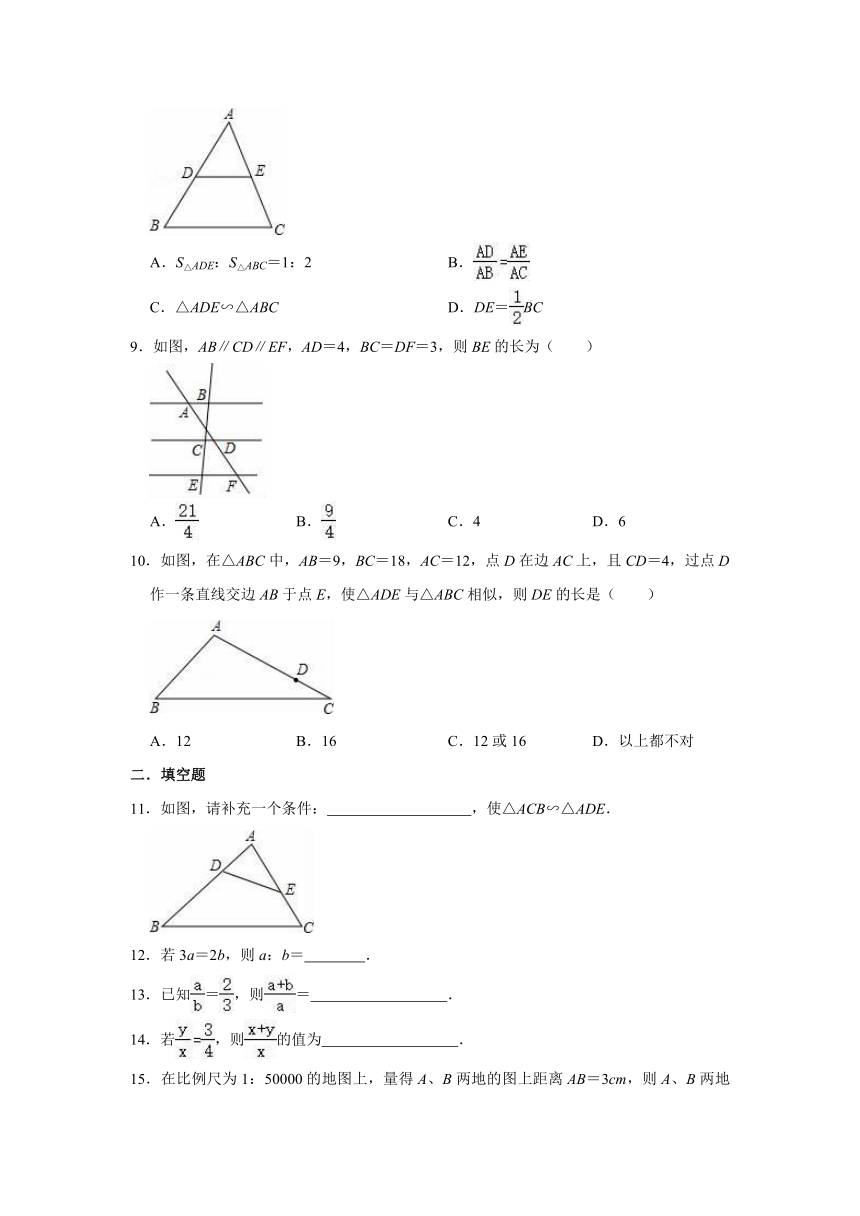

文档简介
2021-2022学年沪科新版九年级上册数学《第22章 相似形》单元测试卷
一.选择题
1.如果x:y=3:5,那么x:(x+y)=( )
A. B. C. D.
2.若=,则的值为( )
A. B. C. D.﹣
3.已知,则的值为( )
A. B. C. D.
4.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则d的长度为( )
A.4cm B.5cm C.6cm D.9cm
5.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
A.AB2=AC BC B.BC2=AC BC C.AC=BC D.BC=AC
6.下列判断中,正确的个数有( )
(1)全等三角形是相似三角形 (2)顶角相等的两个等腰三角形相似
(3)所有的等边三角形都相似 (4)所有的矩形都相似.
A.1个 B.2个 C.3个 D.4个
7.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对 B.5对 C.4对 D.3对
8.如图,在△ABC中,D,E分别是AB,AC的中点,下列说法中不正确的是( )
A.S△ADE:S△ABC=1:2 B.
C.△ADE∽△ABC D.DE=BC
9.如图,AB∥CD∥EF,AD=4,BC=DF=3,则BE的长为( )
A. B. C.4 D.6
10.如图,在△ABC中,AB=9,BC=18,AC=12,点D在边AC上,且CD=4,过点D作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是( )
A.12 B.16 C.12或16 D.以上都不对
二.填空题
11.如图,请补充一个条件: ,使△ACB∽△ADE.
12.若3a=2b,则a:b= .
13.已知=,则= .
14.若,则的值为 .
15.在比例尺为1:50000的地图上,量得A、B两地的图上距离AB=3cm,则A、B两地的实际距离为 km.
16.若线段AB=6cm,点C是线段AB的一个黄金分割点(AC>BC),则AC的长为 cm(结果保留根号).
17.已知:AM:MD=4:1,BD:DC=2:3,则AE:EC= .
18.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
19.如图,△ABC是正三角形,D、E分别是BC、AC上的点,当∠ADE= 时,△ABD∽△DCE.
20.如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,∠MON=∠B,若△OMN与△OBC相似,则CM= .
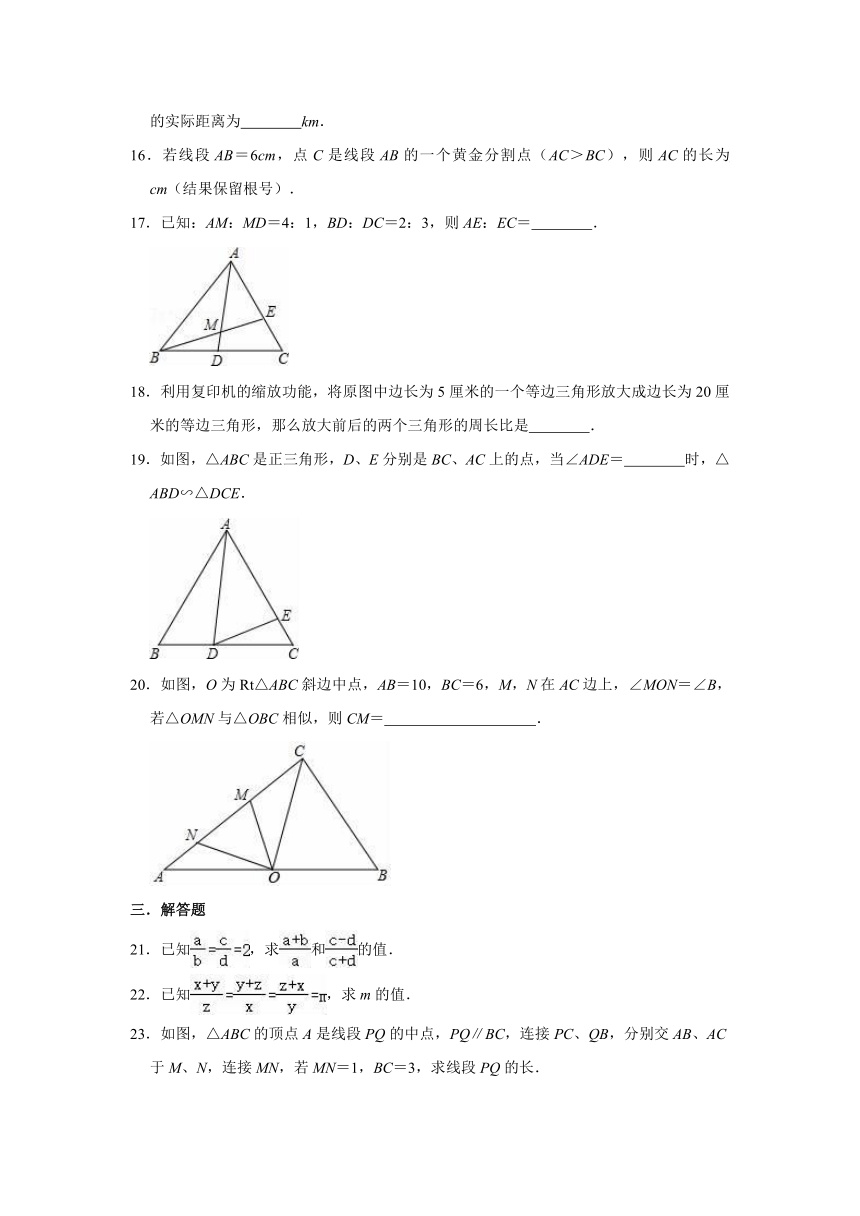
三.解答题
21.已知,求和的值.
22.已知,求m的值.
23.如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.
24.在比例尺是1:3000000的地图上,量得两地之间的距离是10厘米,甲、乙两车同时从两地相向而行,3小时后,两车相遇,已知甲、乙两车的速度比是2:3,甲、乙两车的速度各是多少?
25.已知a、b、c是△ABC的三边,且满足==,且a+b+c=12,请你探索△ABC的形状.
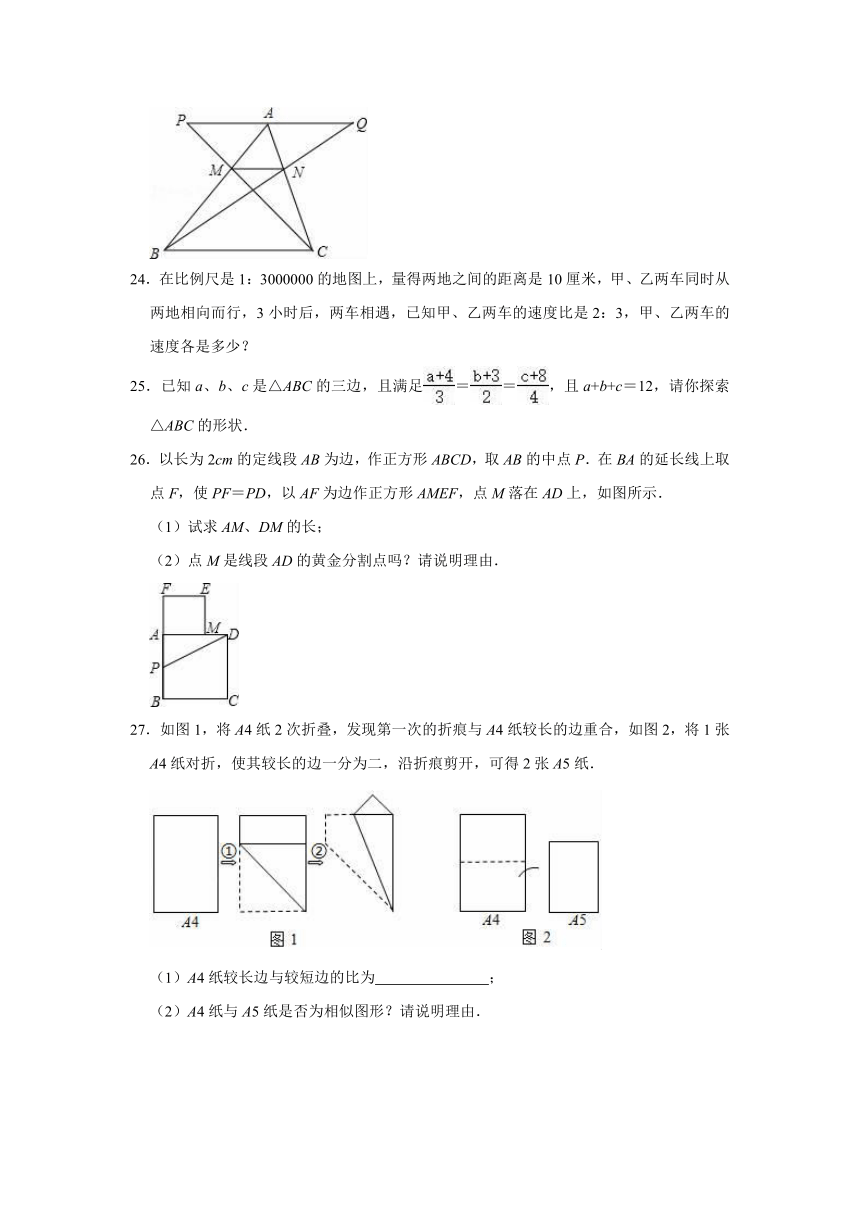
26.以长为2cm的定线段AB为边,作正方形ABCD,取AB的中点P.在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M落在AD上,如图所示.
(1)试求AM、DM的长;
(2)点M是线段AD的黄金分割点吗?请说明理由.
27.如图1,将A4纸2次折叠,发现第一次的折痕与A4纸较长的边重合,如图2,将1张A4纸对折,使其较长的边一分为二,沿折痕剪开,可得2张A5纸.
(1)A4纸较长边与较短边的比为 ;
(2)A4纸与A5纸是否为相似图形?请说明理由.
参考答案与试题解析
一.选择题
1.解:∵x:y=3:5,
∴可设x=3k,则y=5k,
则x:(x+y)=3k:(3k+5k)=3:8;
故选:B.
2.解:由,设a=5x,b=3x,
把a=5x,b=3x代入,
故选:B.
3.解:∵,
∴2m﹣2n=n,
则2m=3n,
∴=,
故选:C.
4.解:因为a,b,c,d是成比例线段,
可得:d=cm,
故选:A.
5.解:∵点C是线段AB的黄金分割点且AC>BC,
∴=,即AC2=BC AB,故A、B错误;
AC=AB,故C错误;
BC=AC,故D正确;
故选:D.
6.解:(1)全等三角形是相似三角形,正确,符合题意;
(2)顶角相等的两个等腰三角形相似,正确,符合题意;
(3)所有的等边三角形都相似,正确,符合题意;
(4)所有的矩形不一定相似,故错误,不符合题意,
正确的有3个,
故选:C.
7.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=∠DCB=90°,
∴∠PCF=90°,
∵BE⊥EF,
∴∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠DEP=90°,
∴∠ABE=∠DEP,
∵AD∥BC,
∴∠DEP=∠F,
∴∠ABE=∠DEP=∠F,
∴△ABE∽△DEP∽△EFB∽△CFP,
∴图中共有相似三角形有6对,
故选:A.
8.解:∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,===,
∴△ADE∽△ABC,DE=BC,
∴=()2=()2=.
故选:A.
9.解:∵AB∥CD∥EF,
∴=,
∴=,
∴EC=,
∴BE=BC+EC=3+=,
故选:A.
10.解:
∵∠A=∠A,
分为两种情况:①DE∥BC(即∠ADE=∠C),
∴△ADE∽△ACB,
∴=,
∴,
∴DE=12,
②∠ADE′=∠B,
∵∠A=∠A,
∴△ADE∽△ABC,
∴=,
∴=,
∴AE=>AB,不合题意,
故选:A.
二.填空题
11.解:当∠ADE=∠C(答案不唯一),再由∠BAC=∠DAE,可得△ACB∽△ADE.
故答案为:∠ADE=∠C(答案不唯一).
12.解:∵3a=2b,
∴a:b=2:3.
故答案为2:3.
13.解:∵=,
∴a=b,
∴==.
故答案为:.
14.解:由合比性质,得
==.
故答案为:.
15.解:∵比例尺为1:50000,量得两地的距离是3厘米,
∴,
∴A、B两地的实际距离=150000cm=1.5km.
故答案为:1.5.
16.解:根据黄金分割点的概念和AC>BC,得:AC=AB=3(﹣1).
故本题答案为:3(﹣1).
17.解:过点D作DF∥BE交AC于F,
∵DF∥BE,
∴△AME∽△ADF,
∴AM:MD=AE:EF=4:1=8:2
∵DF∥BE,
∴△CDF∽△CBE,
∴BD:DC=EF:FC=2:3
∴AE:EC=AE:(EF+FC)=8:(2+3)
∴AE:EC=8:5.
18.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
19.解:当∠ADE=60°时,△ABD∽△DCE;
理由:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=AC,
∵∠B+∠BAD=∠ADE+∠CDE,∠B=∠ADE=60°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE.
20.解:∵∠ACB=90°,AO=OB,
∴OC=OA=OB,
∴∠B=∠OCB,
∵∠MON=∠B,若△OMN与△OBC相似,
∴有两种情形:①如图1中,当∠MON=∠OMN时,
∵∠OMN=∠B,∠OMC+∠OMN=180°,
∴∠OMC+∠B=180°,
∴∠MOB+∠BCM=180°,
∴∠MOB=90°,
∵∠AOM=∠ACB,∠A=∠A,
∴△AOM∽△ACB,
∴=,
∴=,
∴AM=,
∴CM=AC﹣AM=8﹣=.
②如图2中,当∠MON=∠ONM时,
∵∠BOC=∠OMN,
∴∠A+∠ACO=∠ACO+∠MOC,
∴∠MOC=∠A,
∵∠MCO=∠ACO,
∴△OCM∽△ACO,
∴OC2=CM CA,
∴25=CM 8,
∴CM=,
故答案为或.
三.解答题
21.解:∵==2,
∴a=2b,c=2d,
∴==,
==.
22.解:由可知:
x+y=mz,y+z=mx,z+x=my.
这几式相加可得:2(x+y+z)=m(x+y+z),
当x+y+z≠0时,有m=2,
当x+y+z=0时,有x+y=﹣z,y+z=﹣x,x+z=﹣y,m=﹣1.
故m=2或﹣1.
23.解:∵PQ∥BC,
∴,,
∴MN∥BC,
∴==,
∴,
∴,
∵AP=AQ,
∴PQ=3.
24.解:10×3000000=30000000(厘米),
30000000厘米=300千米,
设甲车的速度是2x千米/时,则乙车的速度是3x千米/时,根据题意得
3(2x+3x)=300,
解得x=20,
2x=2×20=40,
3x=3×20=60.
答:甲车的速度是40千米/时,乙车的速度是60千米/时.
25.解:设===k,
可得a=3k﹣4,b=2k﹣3,c=4k﹣8,
代入a+b+c=12得:9k﹣15=12,
解得:k=3,
∴a=5,b=3,c=4,
则△ABC为直角三角形.
26.解:(1)在Rt△APD中,AP=1cm,AD=2cm,
由勾股定理知PD===cm,
∴AM=AF=PF﹣AP=PD﹣AP=﹣1(cm)
DM=AD﹣AM=3﹣(cm);
(2)∵AM2=()2=6﹣2,
AD DM=2×(3﹣)=6﹣2,
∴AM2=AD DM,
所以点M是线段AD的黄金分割点.
27.解:(1)如图1,
由折叠过程可以看到:第一次折叠,A与D重合,四边形ABDC为正方形,折痕BC为对角线,由勾股定理可得BC=AB;第二次折叠,第一次的折痕与A4纸较长的边重合,即BC与较长边重合.所以,较长边=AB.
∴A4纸较长边与较短边的比为:.
故答案为:.
(2)A4纸与A5纸是相似图形.理由:
∵A4纸较长边与较短边的比为:,
∴设A4纸较短边的长为a,则较长边为a.
∵由图2可知:A5纸的长边与A4纸的短边重合,短边等于A4纸的长边的一半,
∴A5纸的长边为a,短边为.
∴A5纸的长边与短边的比为:=.
∴A4纸较长边与较短边的比=A5纸的长边与短边的比.
又∵A4纸与A5纸的四个角均为直角,
∴A4纸与A5纸相似.
一.选择题
1.如果x:y=3:5,那么x:(x+y)=( )
A. B. C. D.
2.若=,则的值为( )
A. B. C. D.﹣
3.已知,则的值为( )
A. B. C. D.
4.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则d的长度为( )
A.4cm B.5cm C.6cm D.9cm
5.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
A.AB2=AC BC B.BC2=AC BC C.AC=BC D.BC=AC
6.下列判断中,正确的个数有( )
(1)全等三角形是相似三角形 (2)顶角相等的两个等腰三角形相似
(3)所有的等边三角形都相似 (4)所有的矩形都相似.
A.1个 B.2个 C.3个 D.4个
7.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对 B.5对 C.4对 D.3对
8.如图,在△ABC中,D,E分别是AB,AC的中点,下列说法中不正确的是( )
A.S△ADE:S△ABC=1:2 B.
C.△ADE∽△ABC D.DE=BC
9.如图,AB∥CD∥EF,AD=4,BC=DF=3,则BE的长为( )
A. B. C.4 D.6
10.如图,在△ABC中,AB=9,BC=18,AC=12,点D在边AC上,且CD=4,过点D作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是( )
A.12 B.16 C.12或16 D.以上都不对
二.填空题
11.如图,请补充一个条件: ,使△ACB∽△ADE.
12.若3a=2b,则a:b= .
13.已知=,则= .
14.若,则的值为 .
15.在比例尺为1:50000的地图上,量得A、B两地的图上距离AB=3cm,则A、B两地的实际距离为 km.
16.若线段AB=6cm,点C是线段AB的一个黄金分割点(AC>BC),则AC的长为 cm(结果保留根号).
17.已知:AM:MD=4:1,BD:DC=2:3,则AE:EC= .
18.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
19.如图,△ABC是正三角形,D、E分别是BC、AC上的点,当∠ADE= 时,△ABD∽△DCE.
20.如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,∠MON=∠B,若△OMN与△OBC相似,则CM= .
三.解答题
21.已知,求和的值.
22.已知,求m的值.
23.如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.
24.在比例尺是1:3000000的地图上,量得两地之间的距离是10厘米,甲、乙两车同时从两地相向而行,3小时后,两车相遇,已知甲、乙两车的速度比是2:3,甲、乙两车的速度各是多少?
25.已知a、b、c是△ABC的三边,且满足==,且a+b+c=12,请你探索△ABC的形状.
26.以长为2cm的定线段AB为边,作正方形ABCD,取AB的中点P.在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M落在AD上,如图所示.
(1)试求AM、DM的长;
(2)点M是线段AD的黄金分割点吗?请说明理由.
27.如图1,将A4纸2次折叠,发现第一次的折痕与A4纸较长的边重合,如图2,将1张A4纸对折,使其较长的边一分为二,沿折痕剪开,可得2张A5纸.
(1)A4纸较长边与较短边的比为 ;
(2)A4纸与A5纸是否为相似图形?请说明理由.
参考答案与试题解析
一.选择题
1.解:∵x:y=3:5,
∴可设x=3k,则y=5k,
则x:(x+y)=3k:(3k+5k)=3:8;
故选:B.
2.解:由,设a=5x,b=3x,
把a=5x,b=3x代入,
故选:B.
3.解:∵,
∴2m﹣2n=n,
则2m=3n,
∴=,
故选:C.
4.解:因为a,b,c,d是成比例线段,
可得:d=cm,
故选:A.
5.解:∵点C是线段AB的黄金分割点且AC>BC,
∴=,即AC2=BC AB,故A、B错误;
AC=AB,故C错误;
BC=AC,故D正确;
故选:D.
6.解:(1)全等三角形是相似三角形,正确,符合题意;
(2)顶角相等的两个等腰三角形相似,正确,符合题意;
(3)所有的等边三角形都相似,正确,符合题意;
(4)所有的矩形不一定相似,故错误,不符合题意,
正确的有3个,
故选:C.
7.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=∠DCB=90°,
∴∠PCF=90°,
∵BE⊥EF,
∴∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠DEP=90°,
∴∠ABE=∠DEP,
∵AD∥BC,
∴∠DEP=∠F,
∴∠ABE=∠DEP=∠F,
∴△ABE∽△DEP∽△EFB∽△CFP,
∴图中共有相似三角形有6对,
故选:A.
8.解:∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,===,
∴△ADE∽△ABC,DE=BC,
∴=()2=()2=.
故选:A.
9.解:∵AB∥CD∥EF,
∴=,
∴=,
∴EC=,
∴BE=BC+EC=3+=,
故选:A.
10.解:
∵∠A=∠A,
分为两种情况:①DE∥BC(即∠ADE=∠C),
∴△ADE∽△ACB,
∴=,
∴,
∴DE=12,
②∠ADE′=∠B,
∵∠A=∠A,
∴△ADE∽△ABC,
∴=,
∴=,
∴AE=>AB,不合题意,
故选:A.
二.填空题
11.解:当∠ADE=∠C(答案不唯一),再由∠BAC=∠DAE,可得△ACB∽△ADE.
故答案为:∠ADE=∠C(答案不唯一).
12.解:∵3a=2b,
∴a:b=2:3.
故答案为2:3.
13.解:∵=,
∴a=b,
∴==.
故答案为:.
14.解:由合比性质,得
==.
故答案为:.
15.解:∵比例尺为1:50000,量得两地的距离是3厘米,
∴,
∴A、B两地的实际距离=150000cm=1.5km.
故答案为:1.5.
16.解:根据黄金分割点的概念和AC>BC,得:AC=AB=3(﹣1).
故本题答案为:3(﹣1).
17.解:过点D作DF∥BE交AC于F,
∵DF∥BE,
∴△AME∽△ADF,
∴AM:MD=AE:EF=4:1=8:2
∵DF∥BE,
∴△CDF∽△CBE,
∴BD:DC=EF:FC=2:3
∴AE:EC=AE:(EF+FC)=8:(2+3)
∴AE:EC=8:5.
18.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
19.解:当∠ADE=60°时,△ABD∽△DCE;
理由:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=AC,
∵∠B+∠BAD=∠ADE+∠CDE,∠B=∠ADE=60°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE.
20.解:∵∠ACB=90°,AO=OB,
∴OC=OA=OB,
∴∠B=∠OCB,
∵∠MON=∠B,若△OMN与△OBC相似,
∴有两种情形:①如图1中,当∠MON=∠OMN时,
∵∠OMN=∠B,∠OMC+∠OMN=180°,
∴∠OMC+∠B=180°,
∴∠MOB+∠BCM=180°,
∴∠MOB=90°,
∵∠AOM=∠ACB,∠A=∠A,
∴△AOM∽△ACB,
∴=,
∴=,
∴AM=,
∴CM=AC﹣AM=8﹣=.
②如图2中,当∠MON=∠ONM时,
∵∠BOC=∠OMN,
∴∠A+∠ACO=∠ACO+∠MOC,
∴∠MOC=∠A,
∵∠MCO=∠ACO,
∴△OCM∽△ACO,
∴OC2=CM CA,
∴25=CM 8,
∴CM=,
故答案为或.
三.解答题
21.解:∵==2,
∴a=2b,c=2d,
∴==,
==.
22.解:由可知:
x+y=mz,y+z=mx,z+x=my.
这几式相加可得:2(x+y+z)=m(x+y+z),
当x+y+z≠0时,有m=2,
当x+y+z=0时,有x+y=﹣z,y+z=﹣x,x+z=﹣y,m=﹣1.
故m=2或﹣1.
23.解:∵PQ∥BC,
∴,,
∴MN∥BC,
∴==,
∴,
∴,
∵AP=AQ,
∴PQ=3.
24.解:10×3000000=30000000(厘米),
30000000厘米=300千米,
设甲车的速度是2x千米/时,则乙车的速度是3x千米/时,根据题意得
3(2x+3x)=300,
解得x=20,
2x=2×20=40,
3x=3×20=60.
答:甲车的速度是40千米/时,乙车的速度是60千米/时.
25.解:设===k,
可得a=3k﹣4,b=2k﹣3,c=4k﹣8,
代入a+b+c=12得:9k﹣15=12,
解得:k=3,
∴a=5,b=3,c=4,
则△ABC为直角三角形.
26.解:(1)在Rt△APD中,AP=1cm,AD=2cm,
由勾股定理知PD===cm,
∴AM=AF=PF﹣AP=PD﹣AP=﹣1(cm)
DM=AD﹣AM=3﹣(cm);
(2)∵AM2=()2=6﹣2,
AD DM=2×(3﹣)=6﹣2,
∴AM2=AD DM,
所以点M是线段AD的黄金分割点.
27.解:(1)如图1,
由折叠过程可以看到:第一次折叠,A与D重合,四边形ABDC为正方形,折痕BC为对角线,由勾股定理可得BC=AB;第二次折叠,第一次的折痕与A4纸较长的边重合,即BC与较长边重合.所以,较长边=AB.
∴A4纸较长边与较短边的比为:.
故答案为:.
(2)A4纸与A5纸是相似图形.理由:
∵A4纸较长边与较短边的比为:,
∴设A4纸较短边的长为a,则较长边为a.
∵由图2可知:A5纸的长边与A4纸的短边重合,短边等于A4纸的长边的一半,
∴A5纸的长边为a,短边为.
∴A5纸的长边与短边的比为:=.
∴A4纸较长边与较短边的比=A5纸的长边与短边的比.
又∵A4纸与A5纸的四个角均为直角,
∴A4纸与A5纸相似.
