6.2.2-待定系数法求反比例函数的解析式精选20题 2021-2022学年北师大版数学九年级上册(Word版含答案)
文档属性
| 名称 | 6.2.2-待定系数法求反比例函数的解析式精选20题 2021-2022学年北师大版数学九年级上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 263.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 19:19:47 | ||
图片预览



文档简介
2021-2022学年北师大九年级数学上册6.2.2-待定系数法求反比例函数的解析式精选20题
1.若反比例函数的图象经过点(m,3m),其中m≠0,则此反比例函数图象经过( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
2.已知关于x的方程(x+1)2+(x﹣b)2=2有唯一实数解,且反比例函数y=的图象,在每个象限内y随x的增大而增大,那么反比例函数的关系式为( )
A.y= B.y= C.y= D.y=
3.已知:如图,直线l经过点A(﹣2,0)和点B(0,1),点M在x轴上,过点M作x轴的垂线交直线l于点C,若OM=2OA,则经过点C的反比例函数表达式为( )
A. B. C. D.
4.如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则该反比例函数的表达式为( )
A.y= B.y= C.y= D.y=
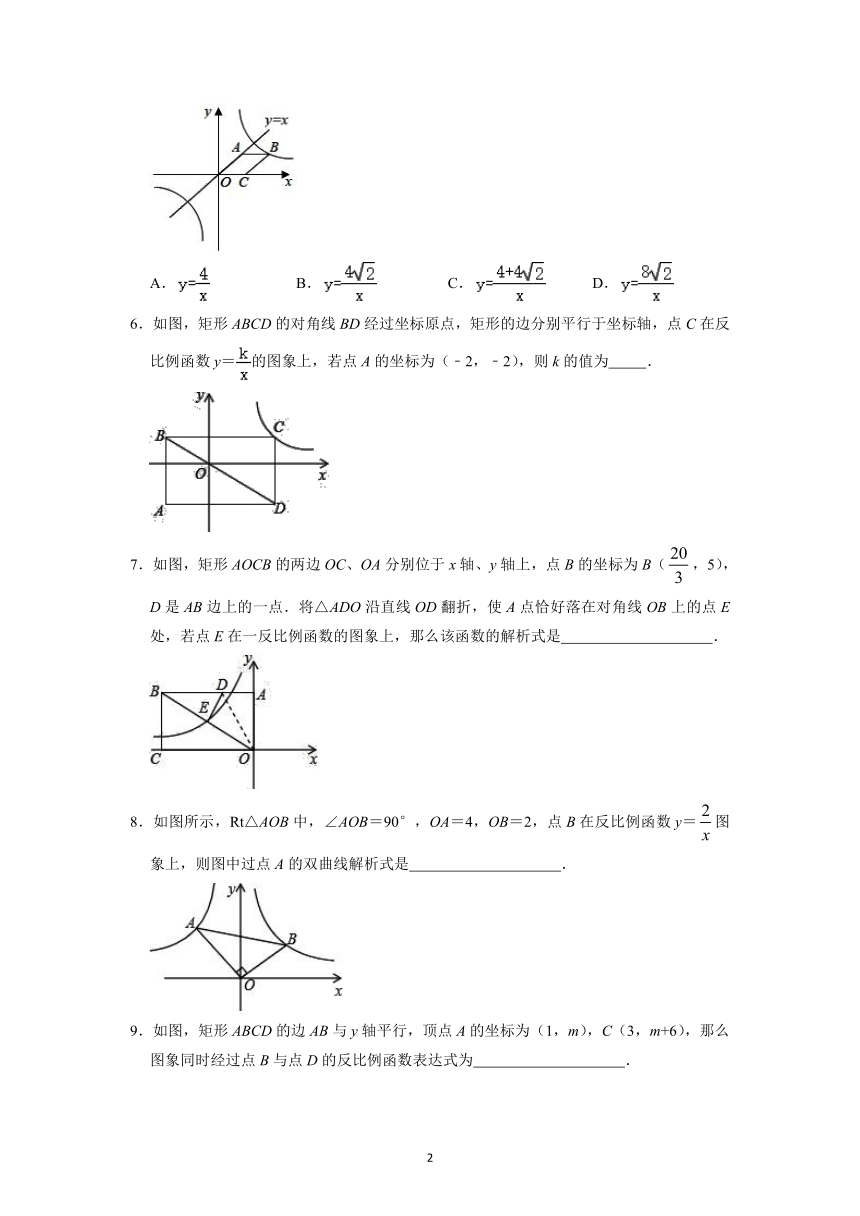
5.如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是4,若反比例函数的图象经过点B,则此反比例函数表达式为( )
A. B. C. D.
6.如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=的图象上,若点A的坐标为(﹣2,﹣2),则k的值为 .
7.如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .
8.如图所示,Rt△AOB中,∠AOB=90°,OA=4,OB=2,点B在反比例函数y=图象上,则图中过点A的双曲线解析式是 .
9.如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,m),C(3,m+6),那么图象同时经过点B与点D的反比例函数表达式为 .
10.如图,双曲线(k>0)经过矩形OABC的边BC的中点E,交AB于点D,若梯形ODBC的面积为3,则双曲线的解析式为 .
11.如图,矩形ABCD的两边AD,AB的长分别为3、8,E是DC的中点,反比例函数的图象经过点E,与AB交于点F.若AF﹣AE=2,则反比例函数的表达式为 .
12.如图,在平面直角坐标系中,已知 ABCD的边AD平行于x轴,A(﹣,2),B(,1),若在第一象限内,反比例函数y=的图象恰好经过C、D两点,则该反比例函数的表达式为 .
13.如图所示,菱形OEFG中,∠GOE=60°,GF=4,点E在y=(k≠0)的图象上,则反比例函数的解析式为 .
14.如图,正方形的中心在直角坐标系的原点,正方形的边与坐标轴平行,点P(3a,a)是正方形与反比例函数图象的一个交点.已知图中阴影部分的面积等于18,则这个反比例函数的表达式为 .
15.如图,点A,D在反比例函数y=的图象上,AB,CD都与y轴垂直,分别交y轴于点B,C.已知点A的坐标(1,m),BC=,CD=,则该反比例函数表达式是 .
16.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.
(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;
(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.
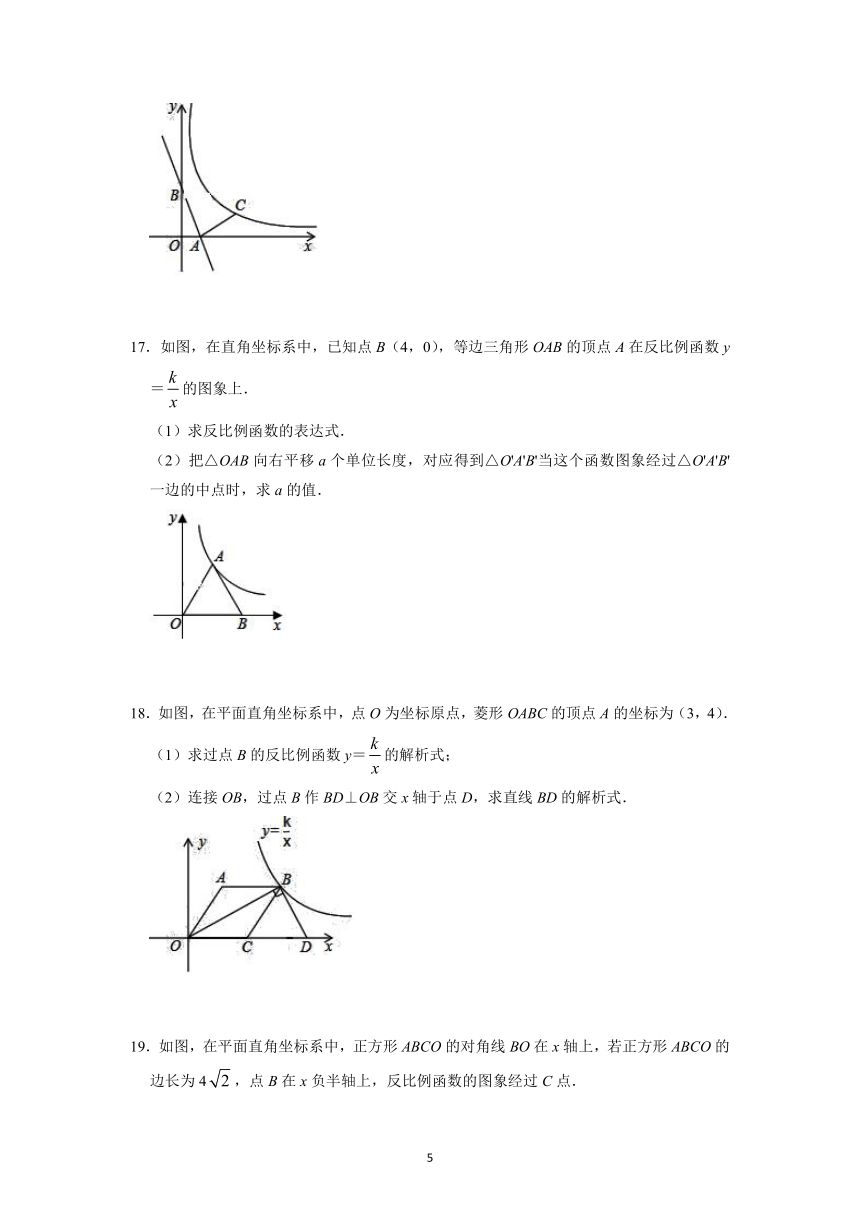
17.如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y=的图象上.
(1)求反比例函数的表达式.
(2)把△OAB向右平移a个单位长度,对应得到△O'A'B'当这个函数图象经过△O'A'B'一边的中点时,求a的值.
18.如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A的坐标为(3,4).
(1)求过点B的反比例函数y=的解析式;
(2)连接OB,过点B作BD⊥OB交x轴于点D,求直线BD的解析式.
19.如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4,点B在x负半轴上,反比例函数的图象经过C点.
(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
20.如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数y=的图象与大正方形的一边交于点A(1,2),且经过小正方形的顶点B.
(1)求反比例函数的解析式;
(2)求图中阴影部分的面积.
参考答案
A 2.B 3.B 4.A 5.C 6.4 7.y= 8.y=﹣ 9.y=
10.y= 11.y=﹣ 12. 13.y=﹣ 14.y= 15.y=
16.解:(1)将点A(1,0),点B(0,2),代入y=mx+b,
∴b=2,m=﹣2,
∴y=﹣2x+2;
∵过点C作CD⊥x轴,
∵线段AB绕点A顺时针旋转90°得到线段AC,
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=1,
∴C(3,1),
∴k=3,
∴y=;
(2)设与AB平行的直线y=﹣2x+h,
联立﹣2x+h=,
∴﹣2x2+hx﹣3=0,
当△=h2﹣24=0时,h=2或﹣2(舍弃),此时点P到直线AB距离最短,
∴﹣2x2+2x﹣3=0,
解得x=,
∴P(,);
17.解:(1)过点A作AC⊥OB于点C,
∵△OAB是等边三角形,
∴∠AOB=60°,OC=OB,
∵B(4,0),
∴OB=OA=4,
∴OC=2,AC=2.
把点A(2,2)代入y=,得k=4.
∴反比例函数的解析式为y=;
(2)分两种情况讨论:
①点D是A′B′的中点,过点D作DE⊥x轴于点E.
由题意得A′B′=4,∠A′B′E=60°,
在Rt△DEB′中,B′D=2,DE=,B′E=1.
∴O′E=3,
把y=代入y=,得x=4,
∴OE=4,
∴a=OO′=1;
②如图3,点F是A′O′的中点,过点F作FH⊥x轴于点H.
由题意得A′O′=4,∠A′O′B′=60°,
在Rt△FO′H中,FH=,O′H=1.
把y=代入y=,得x=4,
∴OH=4,
∴a=OO′=3,
综上所述,a的值为1或3.
18.解:(1)过点A作AE⊥x轴,过B作BF⊥x轴,垂足分别为E,F,如图,
∵A(3,4),
∴OE=3,AE=4,
∴,
∵四边形OABC是菱形,
∴AO=AB=OC=5,AB∥x轴,
∴EF=AB=5,
∴OF=OE+EF=3+5=8,
∴B(8,4),
∵过B点的反比例函数解析式为,
把B点坐标代入得k=32,
∴反比例函数解析式为;
(2)∵OB⊥BD,
∴∠OBD=90°,
∴∠OBF+∠DBF=90°,
∵∠DBF+∠BDF=90°,
∴∠OBF=∠BDF,
又∵∠OFB=∠BFD=90°,
∴△OBF∽△BDF,
∴,
∴,
解得DF=2,
∴OD=OF+DF=8+2=10,
∴D(10,0).
设BD所在直线解析式为y=k1x+b,
把B(8,4),D(10,0)分别代入得:,
解得.
∴直线BD的解析式为y=﹣2x+20.
19.解:(1)连接AC,交x轴于点D,
∵四边形ABCO为正方形,
∴AD=DC=OD=BD,且AC⊥OB,
∵正方形ABCO的边长为4,
∴DC=OD=4,
∴C(﹣4,﹣4),
把C坐标代入反比例函数解析式得:k=16,
则反比例函数解析式为y=;
(2)∵正方形ABCO的边长为4,
∴正方形ABCO的面积为32,
分两种情况考虑:
若P1在第一象限的反比例函数图象上,连接P1B,P1O,
∵S△P1BO=BO |yP|=S正方形ABCO=32,而OB=CO=8,
∴×8×|yP|=32,
∴yP1=8,
把y=8代入反比例函数解析式得:x=2,
此时P1坐标为(2,8);
若P2在第三象限反比例图象上,连接OP2,BP2,
同理得到yP2=﹣8,
把y=﹣8代入反比例函数解析式得:x=﹣2,
此时P2(﹣2,﹣8),
综上所述,点P的坐标为(2,8)或(﹣2,﹣8).
20.解:(1)∵反比例函数的图象经过点A(1,2),
∴2=,
∴k=2,
∴反比例函数的解析式为y=;
(2)∵小正方形的中心与平面直角坐标系的原点O重合,边分别与坐标轴平行,
∴设B点的坐标为(m,m),
∵反比例函数y=的图象经过B点,
∴m=,
∴m2=2,
∴小正方形的面积为4m2=8,
∵大正方形的中心与平面直角坐标系的原点O重合,边分别与坐标轴平行,且A(1,2),
∴大正方形在第一象限的顶点坐标为(2,2),
∴大正方形的面积为4×22=16,
∴图中阴影部分的面积=大正方形的面积﹣小正方形的面积=16﹣8=8.
1.若反比例函数的图象经过点(m,3m),其中m≠0,则此反比例函数图象经过( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
2.已知关于x的方程(x+1)2+(x﹣b)2=2有唯一实数解,且反比例函数y=的图象,在每个象限内y随x的增大而增大,那么反比例函数的关系式为( )
A.y= B.y= C.y= D.y=
3.已知:如图,直线l经过点A(﹣2,0)和点B(0,1),点M在x轴上,过点M作x轴的垂线交直线l于点C,若OM=2OA,则经过点C的反比例函数表达式为( )
A. B. C. D.
4.如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则该反比例函数的表达式为( )
A.y= B.y= C.y= D.y=
5.如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是4,若反比例函数的图象经过点B,则此反比例函数表达式为( )
A. B. C. D.
6.如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=的图象上,若点A的坐标为(﹣2,﹣2),则k的值为 .
7.如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .
8.如图所示,Rt△AOB中,∠AOB=90°,OA=4,OB=2,点B在反比例函数y=图象上,则图中过点A的双曲线解析式是 .
9.如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,m),C(3,m+6),那么图象同时经过点B与点D的反比例函数表达式为 .
10.如图,双曲线(k>0)经过矩形OABC的边BC的中点E,交AB于点D,若梯形ODBC的面积为3,则双曲线的解析式为 .
11.如图,矩形ABCD的两边AD,AB的长分别为3、8,E是DC的中点,反比例函数的图象经过点E,与AB交于点F.若AF﹣AE=2,则反比例函数的表达式为 .
12.如图,在平面直角坐标系中,已知 ABCD的边AD平行于x轴,A(﹣,2),B(,1),若在第一象限内,反比例函数y=的图象恰好经过C、D两点,则该反比例函数的表达式为 .
13.如图所示,菱形OEFG中,∠GOE=60°,GF=4,点E在y=(k≠0)的图象上,则反比例函数的解析式为 .
14.如图,正方形的中心在直角坐标系的原点,正方形的边与坐标轴平行,点P(3a,a)是正方形与反比例函数图象的一个交点.已知图中阴影部分的面积等于18,则这个反比例函数的表达式为 .
15.如图,点A,D在反比例函数y=的图象上,AB,CD都与y轴垂直,分别交y轴于点B,C.已知点A的坐标(1,m),BC=,CD=,则该反比例函数表达式是 .
16.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.
(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;
(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.
17.如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y=的图象上.
(1)求反比例函数的表达式.
(2)把△OAB向右平移a个单位长度,对应得到△O'A'B'当这个函数图象经过△O'A'B'一边的中点时,求a的值.
18.如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A的坐标为(3,4).
(1)求过点B的反比例函数y=的解析式;
(2)连接OB,过点B作BD⊥OB交x轴于点D,求直线BD的解析式.
19.如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4,点B在x负半轴上,反比例函数的图象经过C点.
(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
20.如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数y=的图象与大正方形的一边交于点A(1,2),且经过小正方形的顶点B.
(1)求反比例函数的解析式;
(2)求图中阴影部分的面积.
参考答案
A 2.B 3.B 4.A 5.C 6.4 7.y= 8.y=﹣ 9.y=
10.y= 11.y=﹣ 12. 13.y=﹣ 14.y= 15.y=
16.解:(1)将点A(1,0),点B(0,2),代入y=mx+b,
∴b=2,m=﹣2,
∴y=﹣2x+2;
∵过点C作CD⊥x轴,
∵线段AB绕点A顺时针旋转90°得到线段AC,
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=1,
∴C(3,1),
∴k=3,
∴y=;
(2)设与AB平行的直线y=﹣2x+h,
联立﹣2x+h=,
∴﹣2x2+hx﹣3=0,
当△=h2﹣24=0时,h=2或﹣2(舍弃),此时点P到直线AB距离最短,
∴﹣2x2+2x﹣3=0,
解得x=,
∴P(,);
17.解:(1)过点A作AC⊥OB于点C,
∵△OAB是等边三角形,
∴∠AOB=60°,OC=OB,
∵B(4,0),
∴OB=OA=4,
∴OC=2,AC=2.
把点A(2,2)代入y=,得k=4.
∴反比例函数的解析式为y=;
(2)分两种情况讨论:
①点D是A′B′的中点,过点D作DE⊥x轴于点E.
由题意得A′B′=4,∠A′B′E=60°,
在Rt△DEB′中,B′D=2,DE=,B′E=1.
∴O′E=3,
把y=代入y=,得x=4,
∴OE=4,
∴a=OO′=1;
②如图3,点F是A′O′的中点,过点F作FH⊥x轴于点H.
由题意得A′O′=4,∠A′O′B′=60°,
在Rt△FO′H中,FH=,O′H=1.
把y=代入y=,得x=4,
∴OH=4,
∴a=OO′=3,
综上所述,a的值为1或3.
18.解:(1)过点A作AE⊥x轴,过B作BF⊥x轴,垂足分别为E,F,如图,
∵A(3,4),
∴OE=3,AE=4,
∴,
∵四边形OABC是菱形,
∴AO=AB=OC=5,AB∥x轴,
∴EF=AB=5,
∴OF=OE+EF=3+5=8,
∴B(8,4),
∵过B点的反比例函数解析式为,
把B点坐标代入得k=32,
∴反比例函数解析式为;
(2)∵OB⊥BD,
∴∠OBD=90°,
∴∠OBF+∠DBF=90°,
∵∠DBF+∠BDF=90°,
∴∠OBF=∠BDF,
又∵∠OFB=∠BFD=90°,
∴△OBF∽△BDF,
∴,
∴,
解得DF=2,
∴OD=OF+DF=8+2=10,
∴D(10,0).
设BD所在直线解析式为y=k1x+b,
把B(8,4),D(10,0)分别代入得:,
解得.
∴直线BD的解析式为y=﹣2x+20.
19.解:(1)连接AC,交x轴于点D,
∵四边形ABCO为正方形,
∴AD=DC=OD=BD,且AC⊥OB,
∵正方形ABCO的边长为4,
∴DC=OD=4,
∴C(﹣4,﹣4),
把C坐标代入反比例函数解析式得:k=16,
则反比例函数解析式为y=;
(2)∵正方形ABCO的边长为4,
∴正方形ABCO的面积为32,
分两种情况考虑:
若P1在第一象限的反比例函数图象上,连接P1B,P1O,
∵S△P1BO=BO |yP|=S正方形ABCO=32,而OB=CO=8,
∴×8×|yP|=32,
∴yP1=8,
把y=8代入反比例函数解析式得:x=2,
此时P1坐标为(2,8);
若P2在第三象限反比例图象上,连接OP2,BP2,
同理得到yP2=﹣8,
把y=﹣8代入反比例函数解析式得:x=﹣2,
此时P2(﹣2,﹣8),
综上所述,点P的坐标为(2,8)或(﹣2,﹣8).
20.解:(1)∵反比例函数的图象经过点A(1,2),
∴2=,
∴k=2,
∴反比例函数的解析式为y=;
(2)∵小正方形的中心与平面直角坐标系的原点O重合,边分别与坐标轴平行,
∴设B点的坐标为(m,m),
∵反比例函数y=的图象经过B点,
∴m=,
∴m2=2,
∴小正方形的面积为4m2=8,
∵大正方形的中心与平面直角坐标系的原点O重合,边分别与坐标轴平行,且A(1,2),
∴大正方形在第一象限的顶点坐标为(2,2),
∴大正方形的面积为4×22=16,
∴图中阴影部分的面积=大正方形的面积﹣小正方形的面积=16﹣8=8.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
