13.3.1等腰三角形 同步练习2021-2022学年人教版数学八年级上册(Word版含答案)
文档属性
| 名称 | 13.3.1等腰三角形 同步练习2021-2022学年人教版数学八年级上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 504.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 19:22:19 | ||
图片预览



文档简介
等腰三角形
一、单选题
1.等腰三角形的一边长等于4,一边长等于9,则它的周长是( )
A.17 B.22 C.17或22 D.13
2.如图,中,,,BD、CE分别为与的角平分线,且相交于点F,则图中的等腰三角形有( )
A.6个 B.7个 C.8个 D.9个
3.如图,AC的垂直平分线分别交BC、AC于点D和点E,连接AD,BD=CD,∠C=30°,则∠BAD的度数是( )
A.50° B.60° C.80° D.100°
4.如图,N,C,A三点在同一直线上,△ABC中,∠A:∠ABC:∠ACB=3:5:10.若△MNC≌△ABC,则∠BCM的度数为( )
A.20° B.25° C.28° D.30°
5.如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG的度数是( )
A.10° B.20° C.30° D.40°
6.已知∶如图,在中,,,.以点B为圆心,为半径画弧,交于点D,则线段的长为( )
A.2 B.3 C.5 D.6
7.如图在ABC中,AB=AC,点O为边BC上的任一点,过点O作OE⊥AB,OF⊥AC,垂足分别为E、F,已知腰长为6,面积为15,则OE+OF=( )
A.5 B.7.5 C.9 D.10
8.如图,在三角形纸片ABC中,AC=BC,把△ABC沿着AC翻折,点B落在点D处,连接BD.如果∠BAC=40°,则∠CBD的度数为( )
A.5° B.10° C.15° D.20°
9.如图,在Rt中,,,以点B为圆心,BA长为半径画弧,交CB于点T,连接AT,则的度数是( )
A.64° B.24° C.21° D.16°
10.如图,ABC中,AB=7,AC=5,BC=10,OB平分∠ABC,OC平分∠ACB,MN经过点O,与AB,AC相交于点M,N,且MNBC,则AMN的周长等于( )
A.17 B.15 C.12 D.11
11.已知:中,,为边上一点,,,于,延长线交于,则的长为( )
A. B. C. D.
12.如图,在等腰直角ABC中,∠CBA=90°,BA=BC,延长AB至点D,使得AD=AC,连接CD,ACD的中线AE与BC交于点F,连接DF,过点B作BG∥DF交AC于点G,连接DG,FG.则下列说法正确的个数为( )
①∠BCD=∠CAE;②点G为AC中点;③AF=2DE;④AB=BD+DF;⑤.
A.2个 B.3个 C.4个 D.5个
二、填空题
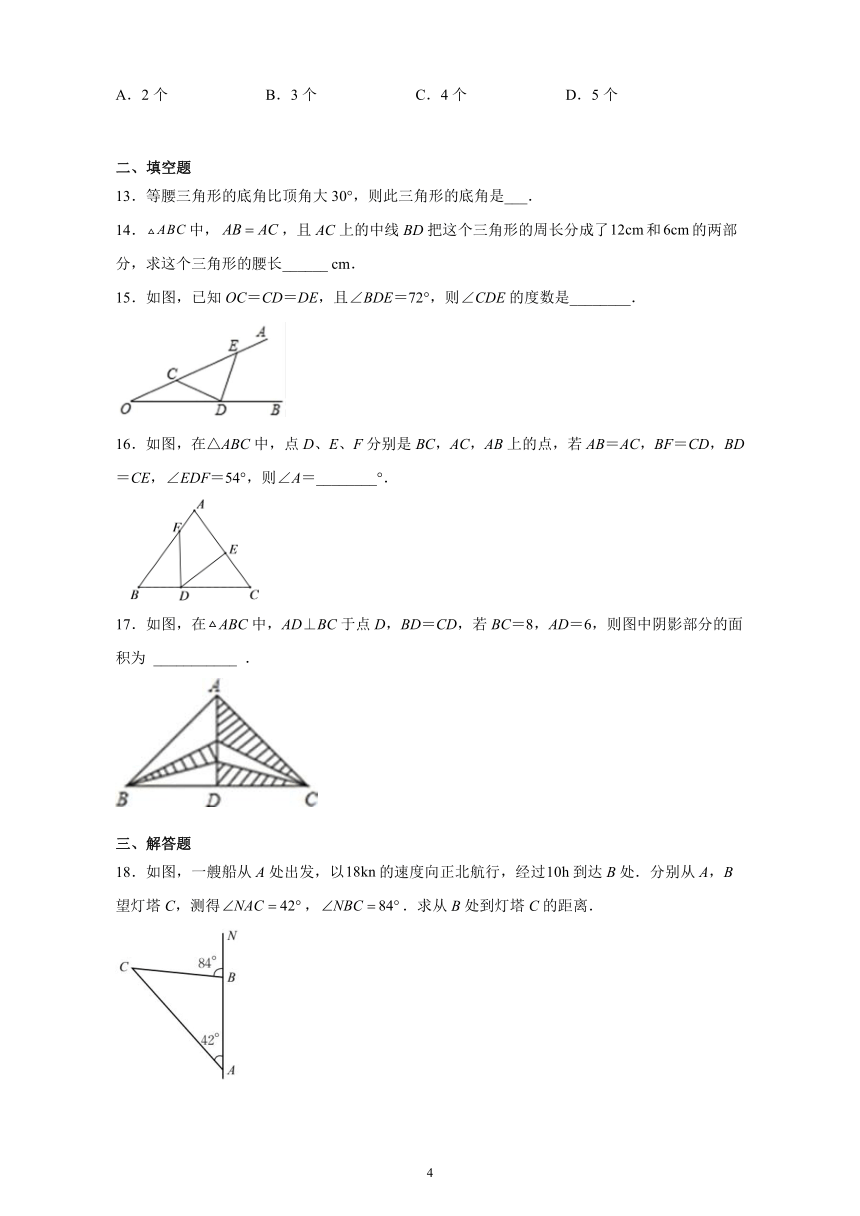
13.等腰三角形的底角比顶角大30°,则此三角形的底角是___.
14.中,,且AC上的中线BD把这个三角形的周长分成了和的两部分,求这个三角形的腰长______ cm.
15.如图,已知OC=CD=DE,且∠BDE=72°,则∠CDE的度数是________.
16.如图,在△ABC中,点D、E、F分别是BC,AC,AB上的点,若AB=AC,BF=CD,BD=CE,∠EDF=54°,则∠A=________°.
17.如图,在ABC中,AD⊥BC于点D,BD=CD,若BC=8,AD=6,则图中阴影部分的面积为 ___________ .
三、解答题
18.如图,一艘船从A处出发,以的速度向正北航行,经过到达B处.分别从A,B望灯塔C,测得,.求从B处到灯塔C的距离.
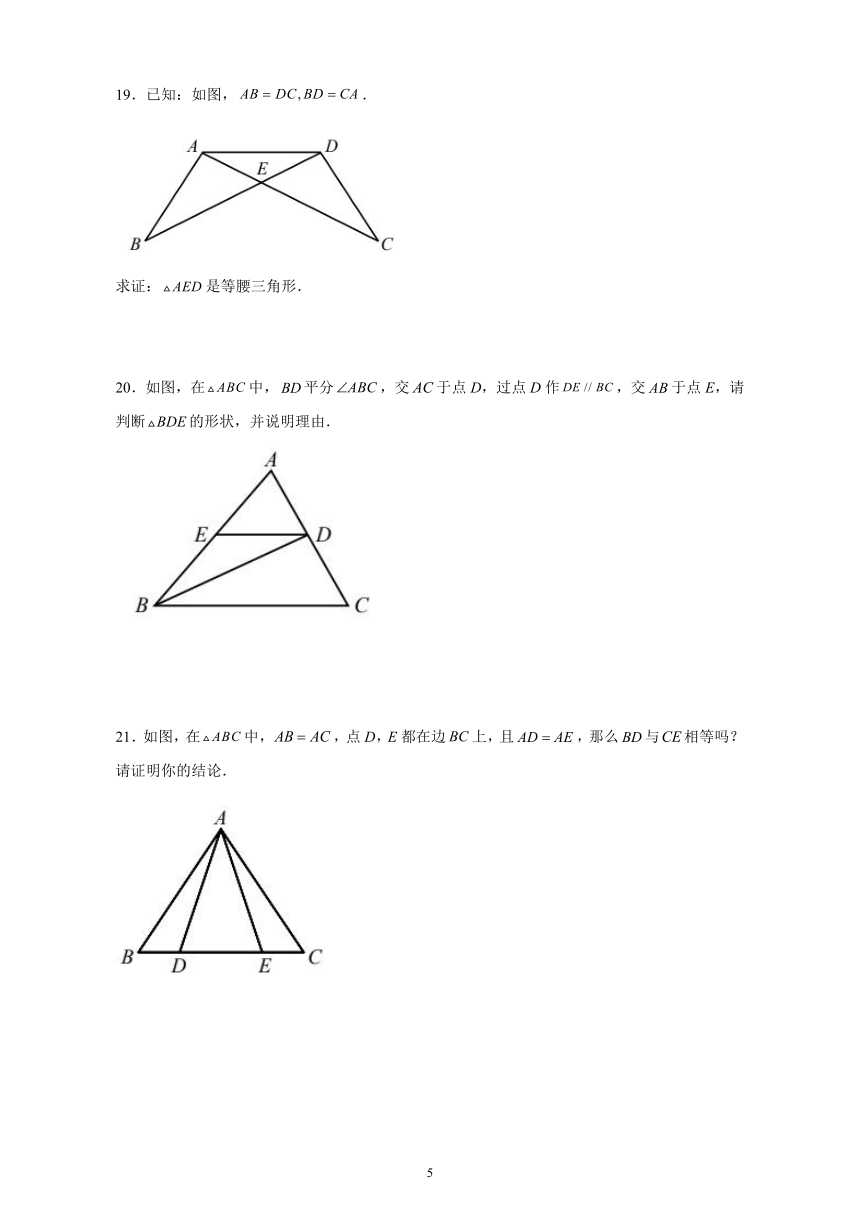
19.已知:如图,.
求证:是等腰三角形.
20.如图,在中,平分,交于点D,过点D作,交于点E,请判断的形状,并说明理由.
21.如图,在中,,点D,E都在边上,且,那么与相等吗?请证明你的结论.
22.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若∠BDE=40°,求∠BAC的度数.
23.在中,,,,D为上一点,连接,过点C作于点E.
(1)如图1,过点B作交的延长线于点F,求证:;
(2)如图2,若D为的中点,的延长线交于点M,连接.求证:;
参考答案
1.B
解:分两种情况:
当腰为4时,,所以不能构成三角形;
当腰为9时,,,所以能构成三角形,周长是:.
故选:B.
2.C
解:∵在ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB==72°,
∵BD、CE分别为∠ABC与∠ACB的角平分线,
∴∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,
∴AE=CE,AD=BD,BF=CF,
∴ABC,ABD,ACE,BFC是等腰三角形,
∵∠BEC=180°﹣∠ABC﹣∠BCE=72°,∠CDB=180°﹣∠BCD﹣∠CBD=72°,∠EFB=∠DFC=∠CBD+∠BCE=72°,
∴∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,
∴BE=BF,CF=CD,BC=BD=CE,
∴BEF,CDF,BCD,CBE是等腰三角形.
∴图中的等腰三角形有8个.
故选:C.
3.B
解:∵的垂直平分线分别交、于点和点,
∴,
∵,
∴.
∵是的外角,
∴.
∵,
∴,
∴,
∴
∴.
故选:B.
4.A
解:∵在△ABC中,∠A:∠ABC:∠ACB=3:5:10,∠A+∠ABC+∠ACB=180°,
∴∠A=30°,∠BCA=100°,∠ABC=50°,
∵△MNC≌△ABC,
∴∠NCM=∠ACB=100°,∠N=∠ABC=50°,BC=NC,
∴∠NBC=∠N=50°,
∴∠BCN=180° ∠N ∠NBC=80°,
∴∠BCM=∠NCM ∠BCN=100° 80°=20°.
故选:A.
5.B
解:∵∠BAC=100°,
∴∠C+∠B=180° 100°=80°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EAB=∠B,
同理∠GAC=∠C,
∴∠EAB+∠GAC=∠C+∠B=80°,
∴∠EAG=100° 80°=20°,
故选:B.
6.A
解:,
,
.
由作图可知,,
,
,
,
,
故选:A.
7.A
解:如图所示,连接AO,过点C作,交AB于点H,
∴,
,
解得,
∵,,
∴,,
∵,
∴,
又∵AB=AC,
∴,
故选A.
8.B
解:∵AC=BC,∠BAC=40°,
∵∠ABC=∠BAC=40°,
由折叠的性质可得:∠CAD=∠BAC=40°,AB=AD,
∴∠BAD=∠CAD+∠BAC=80°,
∴∠ABD= (180°﹣∠BAD)=50°,
∴∠CBD=∠ABD﹣∠ABD=10°.
故选:B.
9.C
解:由题意可得,BT=AB,
∴△BTA是等腰三角形,
∵∠CAB=90°,∠C=48°,
∴∠B=90° 48°=42°,
∴
∴∠CAT=∠BTA ∠C=69° 48°=21°,
故选:C.
10.C
解:∵BO平分∠ABC,CO平分∠ACB,
∴∠MBO=∠OBC,∠OCN=∠OCB,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MBO=∠MOB,∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵AB=7,AC=5,
∴△AMN的周长=AM+MN+AN=AB+AC=7+5=12.
故答案为:C.
11.A
解:过点A作AM⊥BD于点M,过点E作EF⊥BC于点F,
∵AB=AD,AM⊥BC,
∴∠BAM=∠DAM,BM=DM,
∵BH⊥AD,
∴∠HBD+∠HDB=90°,
又∵∠HDB+∠MAD=90°,
∴∠HBD=∠MAD,
∴∠HBD=∠BAM=∠MAD,
∵∠C=45°,
∴∠MAC=∠FEC=45°,
∵∠AEB=∠C+∠EBC=45°+∠EBC,∠BAC=∠MAC+∠BAM=45°+∠BAM,
∴∠AEB=∠BAC,
∴AB=BE,
在△ABM和△BEF中,,
∴△ABM≌△BEF(AAS),
∴EF=BM=1,
∴CE=EF=,
故选:A.
12.C
解:∵AD=AC,AE是△ACD的中线,
∴AE⊥CD,∠DAE=∠CAE,
∴∠CEA=90°,AE垂直平分CD,
∴∠BCD+∠CFE=90°,CF=DF,
∵∠CBA=90°,
∴∠DAE+∠BFA=90°,
∵∠CFE=∠BFA,
∴∠BCD=∠DAE,
∴∠BCD=∠CAE,
故①正确;
∵∠CBA=90°,BA=BC,
∴∠CAB=∠BCA=45°,∠FBA=∠DBC=90°,
∵∠BCD=∠DAE,
∴△BCD≌△BAF(ASA),
∴BD=BF,CD=FA,
∵AE是△ACD的中线,
∴CD=FA=2DE,
故③正确;
∵CB=BF+CF,CF=DF,BF=BD,
∴AB=BD+DF,
故④正确;
∵BD=BF,∠DBC=90°,
∴∠BFD=∠BDF=45°,
∵BG∥DF,
∴∠ABG=∠BDF=45°,
∴∠ABG=∠CBG=45°,
∵BA=BC,
∴点G为AC中点,
故②正确;
由图可知
故⑤不正确,
故正确的有①②③④,共计4个.
故选:C.
13.70°
解:设顶角的度数为x°,则底角的度数为(x+30)°,根据题意,
得x+2(x+30)=180,
解得 x=40.
∴x+30=70,
故答案为:70°.
14.8
解:
如图所示,设,,则,
当时,,
解得:,
当时,,
解得:(不能构成三角形),
.
故答案为:8.
15.84°
解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=72°,
∴∠O=∠ODC=24°,
∴.
故答案为:84°.
16.72
解:∵AB=AC,
∴∠B=∠C
在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∵∠FDC=∠B+∠BFD=∠FDE+∠EDC,
∴∠B=∠EDF=54°,
∴∠A=180°﹣∠B﹣∠C=180°﹣54°﹣54°=72°.
故答案为:72.
17.12
解:如图示
在中,,,
,,,
,
在和中,
,
,
,
在和中,
,
,
,
,
,
.
故答案为:12.
18..
解:根据题意得:AB=18×10=,
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC ∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=.
即从B处到灯塔C的距离是.
19.证明见解析
解:∵,
∴.
∴(全等三角形的对应角相等).
∴(等角对等边).
∴是等腰三角形.
20.等腰三角形,理由见解析.
解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE//BC,
∴∠EDB=∠DBC,
∴∠ABD=∠EDB,
∴BE=DE,
∴△BDE是等腰三角形.
21.,证明见解析.
解:,理由如下:
,,
,,
即,
在和中,,
,
,
,
即.
22.(1)见解析;(2)∠BAC=80°.
解:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF;
(2)∵∠BDE=40°,
∴∠B=50°,
∴∠C=50°,
∴∠BAC=100°-50°-50°=80°.
23.(1)见解析;(2)见解析
解:(1)∵BF⊥BC,CE⊥AD,
∴∠AEC=∠CBF=∠ACB=90°,
∴∠CAD+∠ACE=∠BCF+∠ACE=90°,
∴∠CAD=∠BCF,
又∵AC=BC,
∴△ACD≌△CBF(ASA);
(2)过点B作BF⊥BC交CE的延长线于点F,如图所示:
由(1)得:△ACD≌△CBF,
∴∠ADC=∠F,CD=BF,
∵D为BC的中点,
∴CD=BD,
∴BD=BF,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∵∠CBF=90°,
∴∠FBM=90°-45°=45°,
∴∠DBM=∠FBM,
又∵BM=BM,
∴△BDM≌△BFM(SAS),
∴∠BDM=∠F,
∴∠BDM=∠ADC.
一、单选题
1.等腰三角形的一边长等于4,一边长等于9,则它的周长是( )
A.17 B.22 C.17或22 D.13
2.如图,中,,,BD、CE分别为与的角平分线,且相交于点F,则图中的等腰三角形有( )
A.6个 B.7个 C.8个 D.9个
3.如图,AC的垂直平分线分别交BC、AC于点D和点E,连接AD,BD=CD,∠C=30°,则∠BAD的度数是( )
A.50° B.60° C.80° D.100°
4.如图,N,C,A三点在同一直线上,△ABC中,∠A:∠ABC:∠ACB=3:5:10.若△MNC≌△ABC,则∠BCM的度数为( )
A.20° B.25° C.28° D.30°
5.如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG的度数是( )
A.10° B.20° C.30° D.40°
6.已知∶如图,在中,,,.以点B为圆心,为半径画弧,交于点D,则线段的长为( )
A.2 B.3 C.5 D.6
7.如图在ABC中,AB=AC,点O为边BC上的任一点,过点O作OE⊥AB,OF⊥AC,垂足分别为E、F,已知腰长为6,面积为15,则OE+OF=( )
A.5 B.7.5 C.9 D.10
8.如图,在三角形纸片ABC中,AC=BC,把△ABC沿着AC翻折,点B落在点D处,连接BD.如果∠BAC=40°,则∠CBD的度数为( )
A.5° B.10° C.15° D.20°
9.如图,在Rt中,,,以点B为圆心,BA长为半径画弧,交CB于点T,连接AT,则的度数是( )
A.64° B.24° C.21° D.16°
10.如图,ABC中,AB=7,AC=5,BC=10,OB平分∠ABC,OC平分∠ACB,MN经过点O,与AB,AC相交于点M,N,且MNBC,则AMN的周长等于( )
A.17 B.15 C.12 D.11
11.已知:中,,为边上一点,,,于,延长线交于,则的长为( )
A. B. C. D.
12.如图,在等腰直角ABC中,∠CBA=90°,BA=BC,延长AB至点D,使得AD=AC,连接CD,ACD的中线AE与BC交于点F,连接DF,过点B作BG∥DF交AC于点G,连接DG,FG.则下列说法正确的个数为( )
①∠BCD=∠CAE;②点G为AC中点;③AF=2DE;④AB=BD+DF;⑤.
A.2个 B.3个 C.4个 D.5个
二、填空题
13.等腰三角形的底角比顶角大30°,则此三角形的底角是___.
14.中,,且AC上的中线BD把这个三角形的周长分成了和的两部分,求这个三角形的腰长______ cm.
15.如图,已知OC=CD=DE,且∠BDE=72°,则∠CDE的度数是________.
16.如图,在△ABC中,点D、E、F分别是BC,AC,AB上的点,若AB=AC,BF=CD,BD=CE,∠EDF=54°,则∠A=________°.
17.如图,在ABC中,AD⊥BC于点D,BD=CD,若BC=8,AD=6,则图中阴影部分的面积为 ___________ .
三、解答题
18.如图,一艘船从A处出发,以的速度向正北航行,经过到达B处.分别从A,B望灯塔C,测得,.求从B处到灯塔C的距离.
19.已知:如图,.
求证:是等腰三角形.
20.如图,在中,平分,交于点D,过点D作,交于点E,请判断的形状,并说明理由.
21.如图,在中,,点D,E都在边上,且,那么与相等吗?请证明你的结论.
22.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若∠BDE=40°,求∠BAC的度数.
23.在中,,,,D为上一点,连接,过点C作于点E.
(1)如图1,过点B作交的延长线于点F,求证:;
(2)如图2,若D为的中点,的延长线交于点M,连接.求证:;
参考答案
1.B
解:分两种情况:
当腰为4时,,所以不能构成三角形;
当腰为9时,,,所以能构成三角形,周长是:.
故选:B.
2.C
解:∵在ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB==72°,
∵BD、CE分别为∠ABC与∠ACB的角平分线,
∴∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,
∴AE=CE,AD=BD,BF=CF,
∴ABC,ABD,ACE,BFC是等腰三角形,
∵∠BEC=180°﹣∠ABC﹣∠BCE=72°,∠CDB=180°﹣∠BCD﹣∠CBD=72°,∠EFB=∠DFC=∠CBD+∠BCE=72°,
∴∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,
∴BE=BF,CF=CD,BC=BD=CE,
∴BEF,CDF,BCD,CBE是等腰三角形.
∴图中的等腰三角形有8个.
故选:C.
3.B
解:∵的垂直平分线分别交、于点和点,
∴,
∵,
∴.
∵是的外角,
∴.
∵,
∴,
∴,
∴
∴.
故选:B.
4.A
解:∵在△ABC中,∠A:∠ABC:∠ACB=3:5:10,∠A+∠ABC+∠ACB=180°,
∴∠A=30°,∠BCA=100°,∠ABC=50°,
∵△MNC≌△ABC,
∴∠NCM=∠ACB=100°,∠N=∠ABC=50°,BC=NC,
∴∠NBC=∠N=50°,
∴∠BCN=180° ∠N ∠NBC=80°,
∴∠BCM=∠NCM ∠BCN=100° 80°=20°.
故选:A.
5.B
解:∵∠BAC=100°,
∴∠C+∠B=180° 100°=80°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EAB=∠B,
同理∠GAC=∠C,
∴∠EAB+∠GAC=∠C+∠B=80°,
∴∠EAG=100° 80°=20°,
故选:B.
6.A
解:,
,
.
由作图可知,,
,
,
,
,
故选:A.
7.A
解:如图所示,连接AO,过点C作,交AB于点H,
∴,
,
解得,
∵,,
∴,,
∵,
∴,
又∵AB=AC,
∴,
故选A.
8.B
解:∵AC=BC,∠BAC=40°,
∵∠ABC=∠BAC=40°,
由折叠的性质可得:∠CAD=∠BAC=40°,AB=AD,
∴∠BAD=∠CAD+∠BAC=80°,
∴∠ABD= (180°﹣∠BAD)=50°,
∴∠CBD=∠ABD﹣∠ABD=10°.
故选:B.
9.C
解:由题意可得,BT=AB,
∴△BTA是等腰三角形,
∵∠CAB=90°,∠C=48°,
∴∠B=90° 48°=42°,
∴
∴∠CAT=∠BTA ∠C=69° 48°=21°,
故选:C.
10.C
解:∵BO平分∠ABC,CO平分∠ACB,
∴∠MBO=∠OBC,∠OCN=∠OCB,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MBO=∠MOB,∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵AB=7,AC=5,
∴△AMN的周长=AM+MN+AN=AB+AC=7+5=12.
故答案为:C.
11.A
解:过点A作AM⊥BD于点M,过点E作EF⊥BC于点F,
∵AB=AD,AM⊥BC,
∴∠BAM=∠DAM,BM=DM,
∵BH⊥AD,
∴∠HBD+∠HDB=90°,
又∵∠HDB+∠MAD=90°,
∴∠HBD=∠MAD,
∴∠HBD=∠BAM=∠MAD,
∵∠C=45°,
∴∠MAC=∠FEC=45°,
∵∠AEB=∠C+∠EBC=45°+∠EBC,∠BAC=∠MAC+∠BAM=45°+∠BAM,
∴∠AEB=∠BAC,
∴AB=BE,
在△ABM和△BEF中,,
∴△ABM≌△BEF(AAS),
∴EF=BM=1,
∴CE=EF=,
故选:A.
12.C
解:∵AD=AC,AE是△ACD的中线,
∴AE⊥CD,∠DAE=∠CAE,
∴∠CEA=90°,AE垂直平分CD,
∴∠BCD+∠CFE=90°,CF=DF,
∵∠CBA=90°,
∴∠DAE+∠BFA=90°,
∵∠CFE=∠BFA,
∴∠BCD=∠DAE,
∴∠BCD=∠CAE,
故①正确;
∵∠CBA=90°,BA=BC,
∴∠CAB=∠BCA=45°,∠FBA=∠DBC=90°,
∵∠BCD=∠DAE,
∴△BCD≌△BAF(ASA),
∴BD=BF,CD=FA,
∵AE是△ACD的中线,
∴CD=FA=2DE,
故③正确;
∵CB=BF+CF,CF=DF,BF=BD,
∴AB=BD+DF,
故④正确;
∵BD=BF,∠DBC=90°,
∴∠BFD=∠BDF=45°,
∵BG∥DF,
∴∠ABG=∠BDF=45°,
∴∠ABG=∠CBG=45°,
∵BA=BC,
∴点G为AC中点,
故②正确;
由图可知
故⑤不正确,
故正确的有①②③④,共计4个.
故选:C.
13.70°
解:设顶角的度数为x°,则底角的度数为(x+30)°,根据题意,
得x+2(x+30)=180,
解得 x=40.
∴x+30=70,
故答案为:70°.
14.8
解:
如图所示,设,,则,
当时,,
解得:,
当时,,
解得:(不能构成三角形),
.
故答案为:8.
15.84°
解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=72°,
∴∠O=∠ODC=24°,
∴.
故答案为:84°.
16.72
解:∵AB=AC,
∴∠B=∠C
在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∵∠FDC=∠B+∠BFD=∠FDE+∠EDC,
∴∠B=∠EDF=54°,
∴∠A=180°﹣∠B﹣∠C=180°﹣54°﹣54°=72°.
故答案为:72.
17.12
解:如图示
在中,,,
,,,
,
在和中,
,
,
,
在和中,
,
,
,
,
,
.
故答案为:12.
18..
解:根据题意得:AB=18×10=,
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC ∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=.
即从B处到灯塔C的距离是.
19.证明见解析
解:∵,
∴.
∴(全等三角形的对应角相等).
∴(等角对等边).
∴是等腰三角形.
20.等腰三角形,理由见解析.
解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE//BC,
∴∠EDB=∠DBC,
∴∠ABD=∠EDB,
∴BE=DE,
∴△BDE是等腰三角形.
21.,证明见解析.
解:,理由如下:
,,
,,
即,
在和中,,
,
,
,
即.
22.(1)见解析;(2)∠BAC=80°.
解:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF;
(2)∵∠BDE=40°,
∴∠B=50°,
∴∠C=50°,
∴∠BAC=100°-50°-50°=80°.
23.(1)见解析;(2)见解析
解:(1)∵BF⊥BC,CE⊥AD,
∴∠AEC=∠CBF=∠ACB=90°,
∴∠CAD+∠ACE=∠BCF+∠ACE=90°,
∴∠CAD=∠BCF,
又∵AC=BC,
∴△ACD≌△CBF(ASA);
(2)过点B作BF⊥BC交CE的延长线于点F,如图所示:
由(1)得:△ACD≌△CBF,
∴∠ADC=∠F,CD=BF,
∵D为BC的中点,
∴CD=BD,
∴BD=BF,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∵∠CBF=90°,
∴∠FBM=90°-45°=45°,
∴∠DBM=∠FBM,
又∵BM=BM,
∴△BDM≌△BFM(SAS),
∴∠BDM=∠F,
∴∠BDM=∠ADC.
