2021-2022学年 人教版数学八年级上册13.4.2 造桥选址问题 课件(第四课时 28张)
文档属性
| 名称 | 2021-2022学年 人教版数学八年级上册13.4.2 造桥选址问题 课件(第四课时 28张) |  | |
| 格式 | zip | ||
| 文件大小 | 395.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 10:32:26 | ||
图片预览





文档简介
(共28张PPT)
人教版 数学 八年级上册
第4节 课题学习 最短路径问题
第2课时 造桥选址问题
第十五章 分式
1.两点一线型.
如图,点A,B分别是直线l异侧的两个点,在直线l上找一点C,使得AC+BC的值最小,此时点C就是线段AB与直线l的交点.
B
l
A
C
复习旧知
如图,点A,B是直线l同侧的两点,在直线l上找一点C使得AC+BC的值最小,这时先作点B关于直线l的对称点的B′,连接AB′交直线l于点C,此时点C就是所求作的点.
B′
A
B
l
C
1.两点一线型.
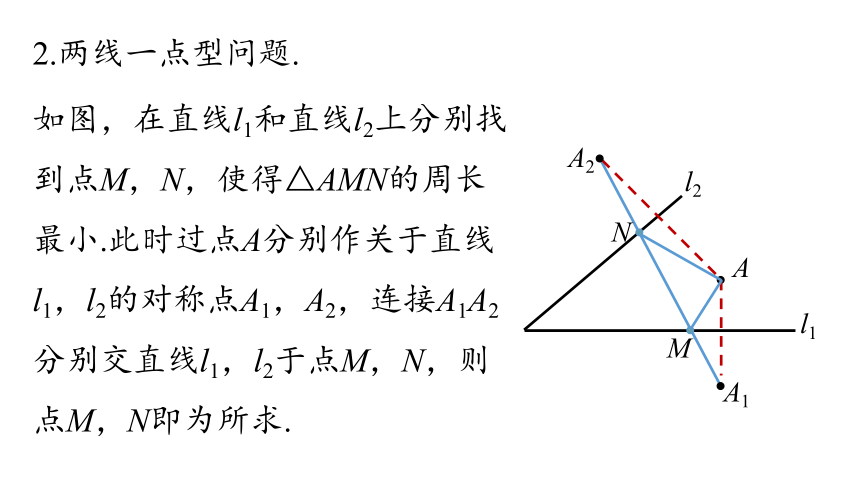
2.两线一点型问题.
如图,在直线l1和直线l2上分别找到点M,N,使得△AMN的周长最小.此时过点A分别作关于直线l1,l2的对称点A1,A2,连接A1A2分别交直线l1,l2于点M,N,则点M,N即为所求.
l1
l2
A
A1
N
A2
M
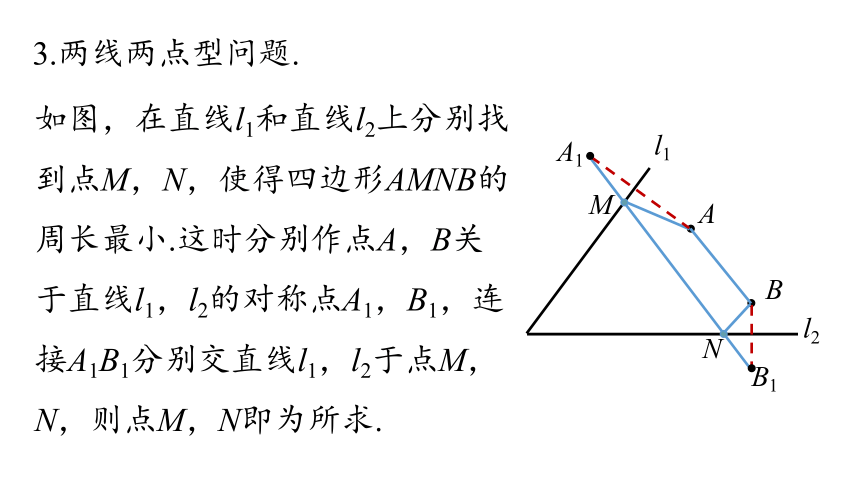
3.两线两点型问题.
如图,在直线l1和直线l2上分别找到点M,N,使得四边形AMNB的周长最小.这时分别作点A,B关于直线l1,l2的对称点A1,B1,连接A1B1分别交直线l1,l2于点M,N,则点M,N即为所求.
l2
l1
B
A
B1
M
A1
N
1.利用轴对称、平移等变化解决简单的最短路径问题.
2.体会图形的变化在解决最值问题中的作用,感受由实际问题转化为数学问题的思想.
学习目标
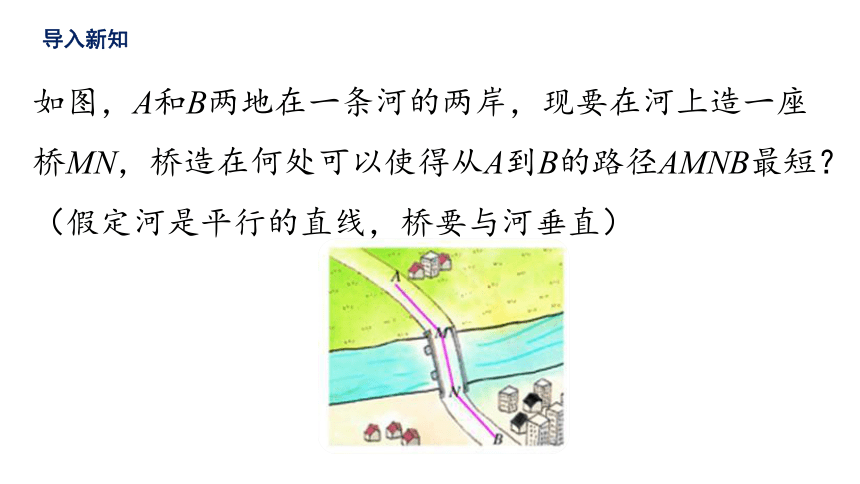
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可以使得从A到B的路径AMNB最短?(假定河是平行的直线,桥要与河垂直)
导入新知
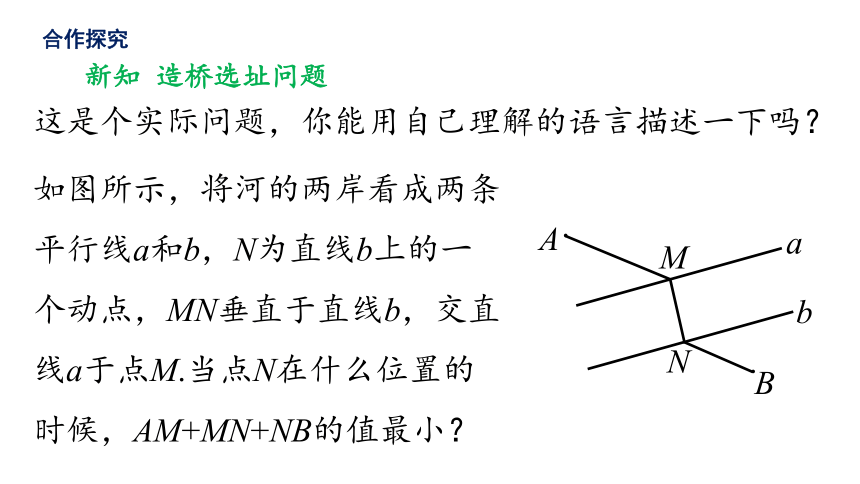
这是个实际问题,你能用自己理解的语言描述一下吗?
如图所示,将河的两岸看成两条平行线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M.当点N在什么位置的时候,AM+MN+NB的值最小?
A
B
a
b
M
N
新知 造桥选址问题
合作探究
分析: 由于河宽是固定的,则MN的大小是固定的.当AM+MN+BN的值最小时,也即AM+BN的值最小.
A
B
a
b
M
N
你能用数学语言说明这个问题所表达的意思吗?
如图,直线a,b满足a//b,点A,点B分别在直线a,b的两侧,MN为直线a,b之间的距离,则点M,N在什么位置的时候,AM+MN+NB的值最小.
A
B
a
b
M
N
分析: 将AM沿着与直线a垂直的方向平移,点M移动到点N,点A移动到点A′,则AA′=MN,AM+NB=A′N+NB.此时问题转化为,当点N在直线b的什么位置时,A′N+ NB的值最小.
A
B
a
b
M
N
A′
如图,连接A′,B,线段A′B最短.因此,线段A′B与直线b的交点即为所求的点N的位置,即在此处造桥MN,所得路径AMNB是最短的.
A
B
a
b
M
N
A′
证明:在直线b上另外任意取一点N′,过点N′作N′M′⊥a,垂足为M′,连接AM′,A′N′,N′B.
∵在△A′N′B中,A′B∴A′N+NB即A′N+NB+MN∴AM+NB+MN即AM+NB+MN的值最小.
A
B
a
b
M
N
A′
M′
N′
如图,从A地到B地要经过一条小河(河的两岸平行),现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从A地到B地的路程最短?
A
B
典例精析
解:(1)如图,过点A作AC垂直于河岸,且使得AC的长等于河宽;
(2)连接BC,与河岸GH相交于点N,且过点N作MN⊥EF于点M,则MN即为所建桥的位置.
F
H
E
G
A
B
M
N
C
最短路径
问题
造桥选址问题
A
B
a
b
M
N
A′
归纳新知
1.如图,l为河岸(视为直线),要想开一条沟将河里的水从A处引到田地里去,则应从河岸l的何处开口才能使水沟最短,找出开口处的位置并说明理由.
解:图略.理由:垂线段最短.
课后练习
2.【中考·黔南州】如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:
①作点B关于直线l的对称点B′;
②连接AB′,与直线l相交于点C,则点C为所求作的点.
在解决这个问题时没有运用到的知识或方法是( )
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
D
3.如图,在△ABC中,AB=5,BC=4,AC=3.
(1)用直尺和圆规作边AB的垂直平分线MN;
解:边AB的垂直平分线MN
如图所示.
(2)在直线MN上找一点D,使△ADC的周长最小,并求出△ADC的最小周长.
解:点D为MN与BC的交点.
∵MN垂直平分AB,
∴AD=BD.
∴△ADC的最小周长为AC+BC=3+4=7.
解:分别作点P关于射线OB,OA所在直线的对称点C,D,连接CD,分别交OA,OB于点M,N,连接OC,OD,PM,PN,如图所示.
4.如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN的周长的最小值是5 cm,求∠AOB的度数.
∵△PMN的周长的最小值是5 cm,∴PM+PN+MN
=5 cm.∴DM+CN+MN=5 cm,即CD=5 cm=OP.
∴OC=OD=CD,即△OCD是等边三角形.
∴∠COD=60°.∴∠AOB=30°.
5.【教材P93复习题T15变式】如图,点P为马厩,AB为草地边缘(下方为草地),CD为一河流,牧马人欲从马厩牵马先去草地吃草,然后到河边饮水,最后回到马厩.请帮他确定一条最佳行走路线.
解:如图所示.
作法:①分别作点P关于AB,CD的对称点P′,P″;
②连接P′P″,分别交AB,CD于点M,N;
③分别连接MP,NP.
∵PM=P′M,PN=P″N,且点P″,N,M,P′在同一条直线上,∴PM+MN+NP=P′P″,
∴P′P″的长即为最小路程.
∴PM—MN—NP为最佳行走路线.
6.如图,AB是∠MON内部的一条线段,在∠MON的两边OM,ON上各取一点C,D组成四边形ABDC,如何取点才能使该四边形的周长最小?
(2)如图②,点A在直线m外侧,点B在直线
m,n内侧,作点B关于直线n的对称点B′,
连接AB′,分别交直线m,n于点P,Q;
(3)如图③,点A,B在直线m,n内侧,分别作点A,B关于直线m,n的对称点A′,B′,
连接A′B′,分别交直线m,n于点P,Q.
解:如图,作A关于射线OM所在直线的对称点E,再作B关于射线ON所在直线的对称点F,连接EF交OM于C,交ON于D,连接AC,BD,则四边形ABDC即为所求.
再 见
人教版 数学 八年级上册
第4节 课题学习 最短路径问题
第2课时 造桥选址问题
第十五章 分式
1.两点一线型.
如图,点A,B分别是直线l异侧的两个点,在直线l上找一点C,使得AC+BC的值最小,此时点C就是线段AB与直线l的交点.
B
l
A
C
复习旧知
如图,点A,B是直线l同侧的两点,在直线l上找一点C使得AC+BC的值最小,这时先作点B关于直线l的对称点的B′,连接AB′交直线l于点C,此时点C就是所求作的点.
B′
A
B
l
C
1.两点一线型.
2.两线一点型问题.
如图,在直线l1和直线l2上分别找到点M,N,使得△AMN的周长最小.此时过点A分别作关于直线l1,l2的对称点A1,A2,连接A1A2分别交直线l1,l2于点M,N,则点M,N即为所求.
l1
l2
A
A1
N
A2
M
3.两线两点型问题.
如图,在直线l1和直线l2上分别找到点M,N,使得四边形AMNB的周长最小.这时分别作点A,B关于直线l1,l2的对称点A1,B1,连接A1B1分别交直线l1,l2于点M,N,则点M,N即为所求.
l2
l1
B
A
B1
M
A1
N
1.利用轴对称、平移等变化解决简单的最短路径问题.
2.体会图形的变化在解决最值问题中的作用,感受由实际问题转化为数学问题的思想.
学习目标
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可以使得从A到B的路径AMNB最短?(假定河是平行的直线,桥要与河垂直)
导入新知
这是个实际问题,你能用自己理解的语言描述一下吗?
如图所示,将河的两岸看成两条平行线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M.当点N在什么位置的时候,AM+MN+NB的值最小?
A
B
a
b
M
N
新知 造桥选址问题
合作探究
分析: 由于河宽是固定的,则MN的大小是固定的.当AM+MN+BN的值最小时,也即AM+BN的值最小.
A
B
a
b
M
N
你能用数学语言说明这个问题所表达的意思吗?
如图,直线a,b满足a//b,点A,点B分别在直线a,b的两侧,MN为直线a,b之间的距离,则点M,N在什么位置的时候,AM+MN+NB的值最小.
A
B
a
b
M
N
分析: 将AM沿着与直线a垂直的方向平移,点M移动到点N,点A移动到点A′,则AA′=MN,AM+NB=A′N+NB.此时问题转化为,当点N在直线b的什么位置时,A′N+ NB的值最小.
A
B
a
b
M
N
A′
如图,连接A′,B,线段A′B最短.因此,线段A′B与直线b的交点即为所求的点N的位置,即在此处造桥MN,所得路径AMNB是最短的.
A
B
a
b
M
N
A′
证明:在直线b上另外任意取一点N′,过点N′作N′M′⊥a,垂足为M′,连接AM′,A′N′,N′B.
∵在△A′N′B中,A′B
A
B
a
b
M
N
A′
M′
N′
如图,从A地到B地要经过一条小河(河的两岸平行),现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从A地到B地的路程最短?
A
B
典例精析
解:(1)如图,过点A作AC垂直于河岸,且使得AC的长等于河宽;
(2)连接BC,与河岸GH相交于点N,且过点N作MN⊥EF于点M,则MN即为所建桥的位置.
F
H
E
G
A
B
M
N
C
最短路径
问题
造桥选址问题
A
B
a
b
M
N
A′
归纳新知
1.如图,l为河岸(视为直线),要想开一条沟将河里的水从A处引到田地里去,则应从河岸l的何处开口才能使水沟最短,找出开口处的位置并说明理由.
解:图略.理由:垂线段最短.
课后练习
2.【中考·黔南州】如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:
①作点B关于直线l的对称点B′;
②连接AB′,与直线l相交于点C,则点C为所求作的点.
在解决这个问题时没有运用到的知识或方法是( )
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
D
3.如图,在△ABC中,AB=5,BC=4,AC=3.
(1)用直尺和圆规作边AB的垂直平分线MN;
解:边AB的垂直平分线MN
如图所示.
(2)在直线MN上找一点D,使△ADC的周长最小,并求出△ADC的最小周长.
解:点D为MN与BC的交点.
∵MN垂直平分AB,
∴AD=BD.
∴△ADC的最小周长为AC+BC=3+4=7.
解:分别作点P关于射线OB,OA所在直线的对称点C,D,连接CD,分别交OA,OB于点M,N,连接OC,OD,PM,PN,如图所示.
4.如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN的周长的最小值是5 cm,求∠AOB的度数.
∵△PMN的周长的最小值是5 cm,∴PM+PN+MN
=5 cm.∴DM+CN+MN=5 cm,即CD=5 cm=OP.
∴OC=OD=CD,即△OCD是等边三角形.
∴∠COD=60°.∴∠AOB=30°.
5.【教材P93复习题T15变式】如图,点P为马厩,AB为草地边缘(下方为草地),CD为一河流,牧马人欲从马厩牵马先去草地吃草,然后到河边饮水,最后回到马厩.请帮他确定一条最佳行走路线.
解:如图所示.
作法:①分别作点P关于AB,CD的对称点P′,P″;
②连接P′P″,分别交AB,CD于点M,N;
③分别连接MP,NP.
∵PM=P′M,PN=P″N,且点P″,N,M,P′在同一条直线上,∴PM+MN+NP=P′P″,
∴P′P″的长即为最小路程.
∴PM—MN—NP为最佳行走路线.
6.如图,AB是∠MON内部的一条线段,在∠MON的两边OM,ON上各取一点C,D组成四边形ABDC,如何取点才能使该四边形的周长最小?
(2)如图②,点A在直线m外侧,点B在直线
m,n内侧,作点B关于直线n的对称点B′,
连接AB′,分别交直线m,n于点P,Q;
(3)如图③,点A,B在直线m,n内侧,分别作点A,B关于直线m,n的对称点A′,B′,
连接A′B′,分别交直线m,n于点P,Q.
解:如图,作A关于射线OM所在直线的对称点E,再作B关于射线ON所在直线的对称点F,连接EF交OM于C,交ON于D,连接AC,BD,则四边形ABDC即为所求.
再 见
