2021-2022学年人教版数学九年级上册24.1.3 弧、弦、圆心角课件(28张)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.1.3 弧、弦、圆心角课件(28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 10:46:25 | ||
图片预览




文档简介
(共28张PPT)
回顾旧知
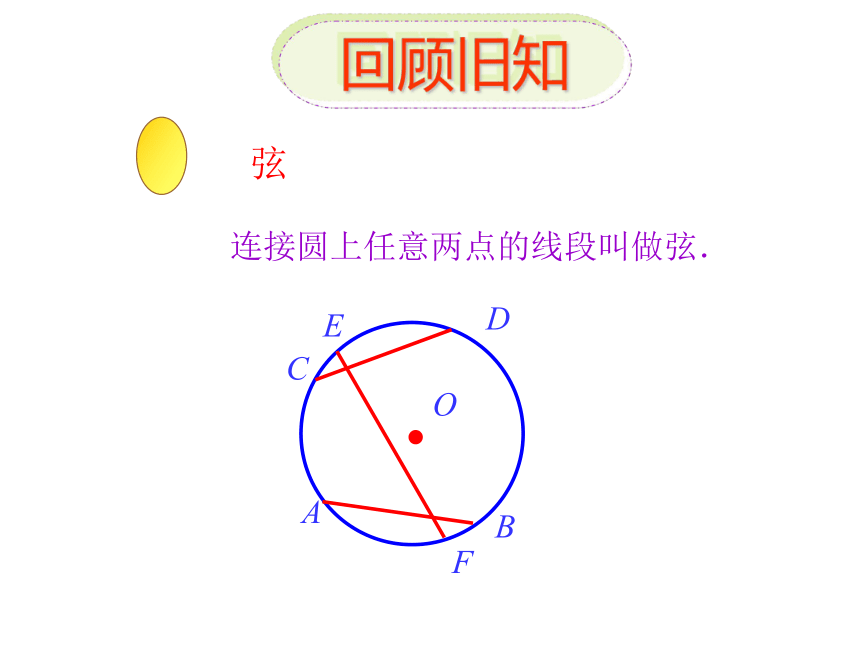
弦
连接圆上任意两点的线段叫做弦.
O
A
B
C
D
E
F
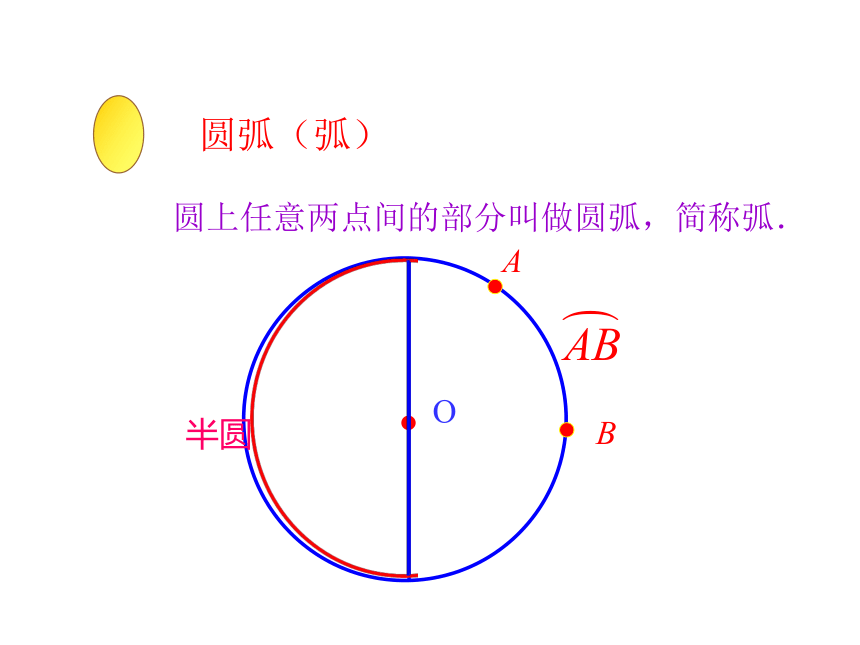
圆上任意两点间的部分叫做圆弧,简称弧.
圆弧(弧)
O
A
B
半圆
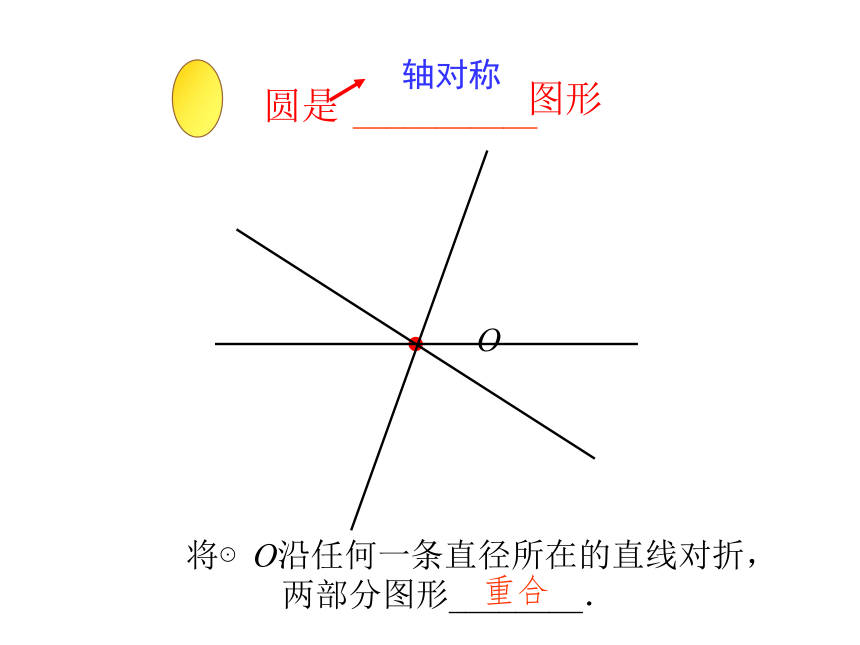
(1)圆是轴对称图形,它的对称轴是过圆心的直线。
忆一忆
一、
圆的对称性如何?(导航17页请你思考1)
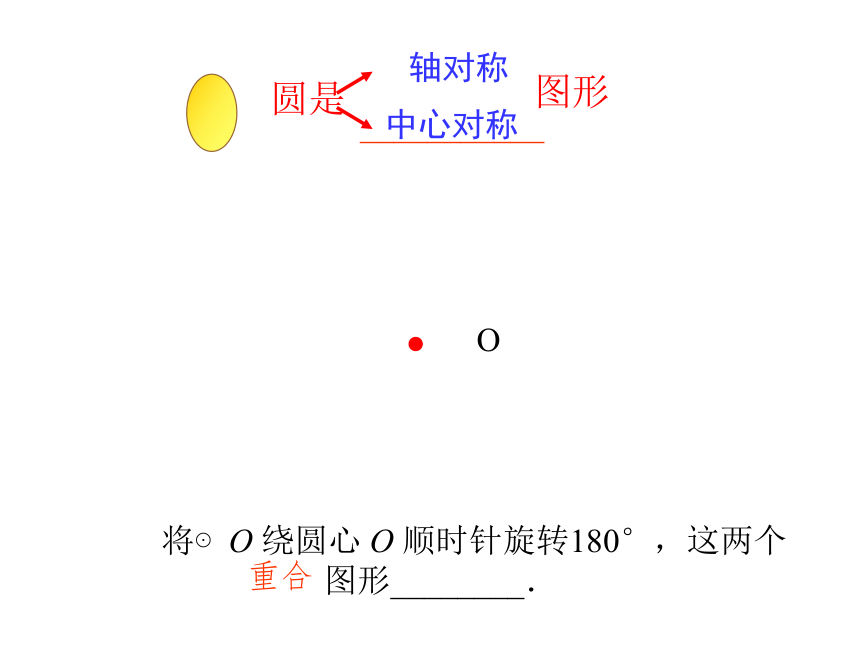
(2)圆是中心对称图形,它的对称中心是圆心。
二、想一想
圆绕着它的圆心旋转多少度就能与原图形重合?
(3)结论:圆绕圆心旋转任意一个角度都能与原
图形重合,这是圆的旋转不变性。
圆是
图形
轴对称
___________
O
将⊙O沿任何一条直径所在的直线对折,两部分图形________.
重合
将⊙O 绕圆心 O 顺时针旋转180°,这两个图形________.
圆是
图形
轴对称
中心对称
___________
O
重合
什么叫圆心角?(导航17页请你思考2)
圆心角 顶点在圆心的角叫圆心角。(如∠AOB).
弦心距 过圆心作弦的垂线,圆心与垂足之间的距离叫弦心距。(如线段OD).
想一想 P94
2
●O
A
B
┓
D
顶点在圆心的角.
·
O
B
A
圆心角
·
O
B
A
·
O
B
A
·
O
B
A
圆心到弦的距离(即圆心到弦的垂线段的距离).
弦心距
·
O
B
A
┓
C
·
O
B
A
┓
C
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时, ∠AOB=∠A′OB′,射线 OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,∴点 A与 A′重合,B与B′重合.
·
O
A
B
做一做
·
O
A
B
A′
B′
A′
B′
三、
∴弧AB与弧A'B'重合,AB与A′B′重合.
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?(导航17页请你思考3)
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
C
A′
B′
C′
┏
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
知识要点
弧、弦、圆心角的关系定理
弧、弦与圆心角的关系定理(等对等定理)
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
四、说一说
五、议一议
定理“在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦也相等”中,可否
把条件“在同圆或等圆中”去掉?为什么?
不能去掉.
反例:如图,虽然∠AOB=∠A′O′B′,
但AB≠A′B′,弧AB≠弧A′B′
定理“在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦也相等”中,可否
把条件“在同圆或等圆中”去掉?为什么?
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
弧、弦、圆心角关系定理的推论
在同圆或等圆中,相等的弦心距所对的圆心角相等,所对的弧相等,所对的弦相等.
在同圆或等圆中,有一组关系相等,那么所对应的其它各组关系均分别相等.
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
两个圆心角相等
两条弧相等
两条弦相等
两条弦心距相等
这四组关系分别轮换,其它关系是否成立
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
弧、弦、圆心角关系定理的推论
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等.
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
弧、弦、圆心角关系定理的推论
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等.
推论
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.
猜一猜P96
6
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
在这里可以不说“在同圆或等圆中”吗?
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
四、练习
OE﹦OF
证明:∵ OE⊥AB OF ⊥CD
∵ AB﹦CD ∴ AE﹦CF
∵ OA﹦OC ∴ RT△AOE≌RT △COF
∴ OE﹦OF
证明:
∴ AB=AC.
又∠ACB=60°,
∴ AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
·
A
B
C
O
五、例题
∵
例1 如图,在⊙O中, ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC
如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
解:
六、练习
∵
∵ ∠COD=35°
七、思考
(1)在圆O中,圆心角∠AOB=90°,点O到弦AB的距离为5,则圆O的直径为( )(导航17页请你思考4)
七、思考
(2)如图,圆O的两条弦AB、CD互相垂直且交于点P,OE垂直于AB,OF垂直于CD,垂足分别是E、F,且弧AC=弧BD,试探究四边形EOFP的形状,并说明理由。(导航17页请你思考5)
七、思考
(3)如图点O是∠EPF的角平分线上的一点,圆O与∠EPF的两边分别交于点A,B,C,D,根据上述条件,可以推出( )(要求:尽可能地写出你认为正确的结论即可,不再标注其他字母,不写推理过程)(导航17页请你思考6)
°
七、思考
(4) 如图,已知AB、CD为⊙O的两条弦,弧AD=弧BC, 求证AB=CD
(5)如图,已知OA、OB是⊙O的半径,点C为AB的中点,M、N分别为OA、OB的中点,求证:MC=NC
⌒
(6)如图,BC为⊙O的直径,OA是⊙O的半径,弦BE∥OA,
求证:AC=AE
⌒ ⌒
1、等对等定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
2、等对等定理的推论:在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.
3、应用
4、数学思想:数形结合思想
八、点一点
回顾旧知
弦
连接圆上任意两点的线段叫做弦.
O
A
B
C
D
E
F
圆上任意两点间的部分叫做圆弧,简称弧.
圆弧(弧)
O
A
B
半圆
(1)圆是轴对称图形,它的对称轴是过圆心的直线。
忆一忆
一、
圆的对称性如何?(导航17页请你思考1)
(2)圆是中心对称图形,它的对称中心是圆心。
二、想一想
圆绕着它的圆心旋转多少度就能与原图形重合?
(3)结论:圆绕圆心旋转任意一个角度都能与原
图形重合,这是圆的旋转不变性。
圆是
图形
轴对称
___________
O
将⊙O沿任何一条直径所在的直线对折,两部分图形________.
重合
将⊙O 绕圆心 O 顺时针旋转180°,这两个图形________.
圆是
图形
轴对称
中心对称
___________
O
重合
什么叫圆心角?(导航17页请你思考2)
圆心角 顶点在圆心的角叫圆心角。(如∠AOB).
弦心距 过圆心作弦的垂线,圆心与垂足之间的距离叫弦心距。(如线段OD).
想一想 P94
2
●O
A
B
┓
D
顶点在圆心的角.
·
O
B
A
圆心角
·
O
B
A
·
O
B
A
·
O
B
A
圆心到弦的距离(即圆心到弦的垂线段的距离).
弦心距
·
O
B
A
┓
C
·
O
B
A
┓
C
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时, ∠AOB=∠A′OB′,射线 OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,∴点 A与 A′重合,B与B′重合.
·
O
A
B
做一做
·
O
A
B
A′
B′
A′
B′
三、
∴弧AB与弧A'B'重合,AB与A′B′重合.
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?(导航17页请你思考3)
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
C
A′
B′
C′
┏
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
知识要点
弧、弦、圆心角的关系定理
弧、弦与圆心角的关系定理(等对等定理)
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
四、说一说
五、议一议
定理“在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦也相等”中,可否
把条件“在同圆或等圆中”去掉?为什么?
不能去掉.
反例:如图,虽然∠AOB=∠A′O′B′,
但AB≠A′B′,弧AB≠弧A′B′
定理“在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦也相等”中,可否
把条件“在同圆或等圆中”去掉?为什么?
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
弧、弦、圆心角关系定理的推论
在同圆或等圆中,相等的弦心距所对的圆心角相等,所对的弧相等,所对的弦相等.
在同圆或等圆中,有一组关系相等,那么所对应的其它各组关系均分别相等.
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
两个圆心角相等
两条弧相等
两条弦相等
两条弦心距相等
这四组关系分别轮换,其它关系是否成立
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
弧、弦、圆心角关系定理的推论
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等.
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
弧、弦、圆心角关系定理的推论
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等.
推论
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.
猜一猜P96
6
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
在这里可以不说“在同圆或等圆中”吗?
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
四、练习
OE﹦OF
证明:∵ OE⊥AB OF ⊥CD
∵ AB﹦CD ∴ AE﹦CF
∵ OA﹦OC ∴ RT△AOE≌RT △COF
∴ OE﹦OF
证明:
∴ AB=AC.
又∠ACB=60°,
∴ AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
·
A
B
C
O
五、例题
∵
例1 如图,在⊙O中, ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC
如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
解:
六、练习
∵
∵ ∠COD=35°
七、思考
(1)在圆O中,圆心角∠AOB=90°,点O到弦AB的距离为5,则圆O的直径为( )(导航17页请你思考4)
七、思考
(2)如图,圆O的两条弦AB、CD互相垂直且交于点P,OE垂直于AB,OF垂直于CD,垂足分别是E、F,且弧AC=弧BD,试探究四边形EOFP的形状,并说明理由。(导航17页请你思考5)
七、思考
(3)如图点O是∠EPF的角平分线上的一点,圆O与∠EPF的两边分别交于点A,B,C,D,根据上述条件,可以推出( )(要求:尽可能地写出你认为正确的结论即可,不再标注其他字母,不写推理过程)(导航17页请你思考6)
°
七、思考
(4) 如图,已知AB、CD为⊙O的两条弦,弧AD=弧BC, 求证AB=CD
(5)如图,已知OA、OB是⊙O的半径,点C为AB的中点,M、N分别为OA、OB的中点,求证:MC=NC
⌒
(6)如图,BC为⊙O的直径,OA是⊙O的半径,弦BE∥OA,
求证:AC=AE
⌒ ⌒
1、等对等定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
2、等对等定理的推论:在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.
3、应用
4、数学思想:数形结合思想
八、点一点
同课章节目录
