江西省赣州市第三高级中学2022届高三上学期期中适应考试数学(理)试卷(Word版含答案)
文档属性
| 名称 | 江西省赣州市第三高级中学2022届高三上学期期中适应考试数学(理)试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 17:53:01 | ||
图片预览



文档简介
赣州市第三高级中学2021-2022上学期期中适应性考试
数学(理科)试卷
做题时间:2021年11月
一、单选题
1.已知、,若,则的值为( )
A. B. C. D.或
2.已知是实数,是纯虚数,则 等于
A. B. C. D.
3.已知.则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.函数的零点一定位于区间( )
A. B. C. D.
5.函数对任意都有成立,且函数的图象关于点对称,,则( )
A.1 B.2 C.3 D.4
6.历史上,最伟大的数学家一直都热衷于寻找质数的“分布规律”,法国数学家马林·梅森就是研究质数的数学家中成就很高的一位,正因为他的卓越贡献,现在人们将形如“(p是质数)”的质数称为梅森数,迄今为止共发现了51个梅森数,前4个梅森数分别是,,,,3,7是1位数,31是2位数,127是3位数.已知第10个梅森数为,则第10个梅森数的位数为( )(参考数据:)
A.25 B.29 C.27 D.28
7.已知函数,则函数的图象可能是( )
A. B.
C. D.
8.定义一种运算,将函数的图象向左平移个单位,所得图象对应的函数为偶函数,则的最小值是( )
A. B. C. D.
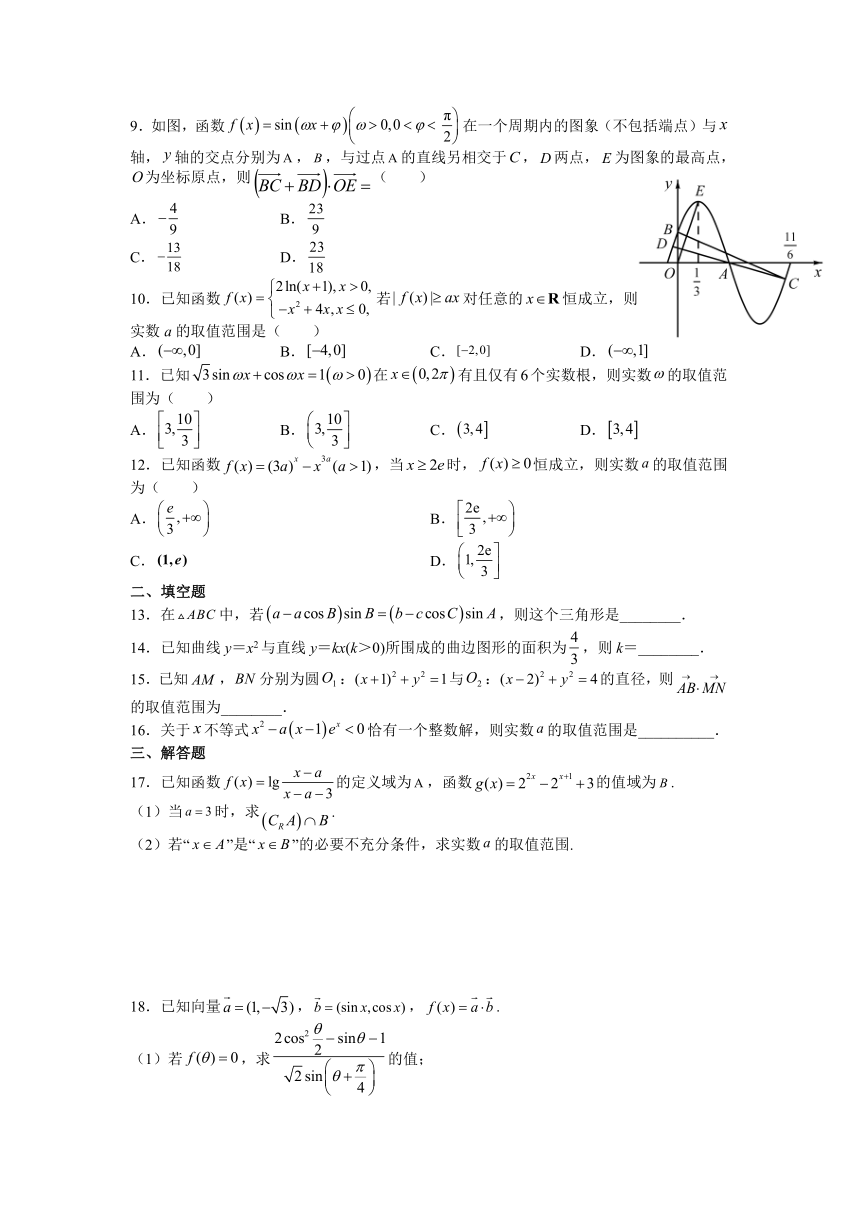
9.如图,函数在一个周期内的图象(不包括端点)与轴,轴的交点分别为,,与过点的直线另相交于,两点,为图象的最高点,为坐标原点,则( )
A. B.
C. D.
10.已知函数若对任意的恒成立,则实数a的取值范围是( )
A. B. C. D.
11.已知在有且仅有个实数根,则实数的取值范围为( )
A. B. C. D.
12.已知函数,当时,恒成立,则实数的取值范围为( )
A. B.
C. D.
二、填空题
13.在中,若,则这个三角形是________.
14.已知曲线y=x2与直线y=kx(k>0)所围成的曲边图形的面积为,则k=________.
15.已知,分别为圆:与:的直径,则的取值范围为________.
16.关于不等式恰有一个整数解,则实数的取值范围是__________.
三、解答题
17.已知函数的定义域为,函数的值域为.
(1)当时,求.
(2)若“”是“”的必要不充分条件,求实数的取值范围.
18.已知向量,,.
(1)若,求的值;
(2)当时,求函数的值域.
19.如图,在平面四边形中,已知,
(1)若平分,且,求的长
(2)若,求的长
20.2020年春节前后,一场突如其来的新冠肺炎疫情在武汉出现并很快地传染开来(已有证据表明2019年10月、11月国外已经存在新冠肺炎病毒),对人类生命形成巨大危害.在中共中央、国务院强有力的组织领导下,全国人民万众一心抗击、防控新冠肺炎,疫情早在3月底已经得到了非常好的控制(累计病亡人数人),然而国外因国家体制、思想观念的不同,防控不力,新冠肺炎疫情越来越严重.疫情期间造成医用防护用品短缺,某厂家生产医用防护用品需投入年固定成本为万元,每生产万件,需另投入成本为.当年产量不足万件时,(万元);当年产量不小于万件时,(万元).通过市场分析,若每件售价为元时,该厂年内生产的商品能全部售完.(利润销售收入总成本)
(1)写出年利润(万元)关于年产量(万件)的函数解析式;
(2)年产量为多少万件时,该厂在这一商品的生产中所获利润最大 并求出利润的最大值.
21.已知函数,其中a为正实数.
(1)若函数在处的切线斜率为2,求a的值;
(2)若函数有两个极值点,,求证:.
22.在直角坐标系中,直线的参数方程为(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为,直线交曲线于两点.
(1)写出直线的极坐标方程和曲线的直角坐标方程;
(2)设点的直角坐标为,若点到两点的距离之积是16,求的值.
23.已知函数.
(1)解不等式;
(2)设函数的最小值为,实数满足,求证:.
期中适应性考试数学(理科)参考答案
1.C 2.D 3.A 4.C 5.D 6.C 7.B 8.C 9.A 10.B 11.B12.D
11、设,
当时,或或.
故方程的正数解由小到大排列为:,,,,,,,…依题意故,故选:B.
12、即,则,则,
令,,
当,,单调递增;
当,,单调递减,
因为,所以,
又,所以恒成立,
故.故选:D.
13.等腰或直角三角形 14.2 15. 16.
15、
.
而
故答案为:
16、①当时,原不等式不成立;
②当时,由恰有一个整数解,得恰有一个整数解.
令,则,因此函数在区间上单调递减,易得不可能只有一个整数解,故不满足;
③当时,由恰有一个整数解,得恰有一个整数解.
由②可知,易得函数在区间上单调递减,在区间上单调递增,故.
又因,且恰有一个整数解,所以,即.
综上,.
故答案为:.
17.(1);(2).
解:(1)由,解得:或,即,
由于,.
当时,,
,.
(2)依题可知,是A的真子集,即 ,
所以,解得:,
所以实数的取值范围为.
18.(1);(2).
(1)因为,,
所以,
因为,所以,所以,所以,
.
(2),因为,所以.
当,即时,取最小值;当,即时,取最大值2.所以当时,函数的值域为.
19.(1)2;(2)5.
解:(1)平分,,
,,在中,,,,
由余弦定理,可得:,解得:,的值为2.
(2),,又,
,
在中,由正弦定理,可得:,即的长为5.
20.(1)当,时,
.
当,时,
.
.
(2)当,时,,
当时,取得最大值(万元)
当,时,
当且仅当,即时等号成立.
即时,取得最大值万元.
综上,所以即生产量为万件时,该厂在这一商品的生产中所获利润最大为万元.
21.(1)1;(2)证明见解析.
解:因为,
所以,
则,所以a的值为
,函数的定义域为,
若,即,则,
此时的单调减区间为;
若,即,则的两根为,
此时的单调减区间为,,
单调增区间为
当时,函数有两个极值点,,且,.
因为
,
要证,只需证
构造函数,则,
在上单调递增,
又,,且在定义域上不间断,
由零点存在定理,可知在上唯一实根,
且在上递减,上递增,所以的最小值为,因为,当时,,所以,
所以恒成立.所以,所以.
22.解:(1)直线的直角坐标方程为,
所以直线的极坐标方程为.
由,得.
所以曲线的直角坐标方程为.
(2)将直线的参数坐标方程代入中,
得.设对应的参数分别为,则.
,或,
23.(1);(2)证明见解析.
(1),即.当时,不等式可化为,解得:
又∵,∴; 当时,不等式可化为,解得:
又∵,∴.当时,不等式可化为,解得:
又∵,∴. 综上所得,或,即.
∴原不等式的解集为.
(2)由绝对值不等式性质得,,
∴,即.
令,则,,
,
等且仅当即时等号成立.
原不等式得证.
数学(理科)试卷
做题时间:2021年11月
一、单选题
1.已知、,若,则的值为( )
A. B. C. D.或
2.已知是实数,是纯虚数,则 等于
A. B. C. D.
3.已知.则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.函数的零点一定位于区间( )
A. B. C. D.
5.函数对任意都有成立,且函数的图象关于点对称,,则( )
A.1 B.2 C.3 D.4
6.历史上,最伟大的数学家一直都热衷于寻找质数的“分布规律”,法国数学家马林·梅森就是研究质数的数学家中成就很高的一位,正因为他的卓越贡献,现在人们将形如“(p是质数)”的质数称为梅森数,迄今为止共发现了51个梅森数,前4个梅森数分别是,,,,3,7是1位数,31是2位数,127是3位数.已知第10个梅森数为,则第10个梅森数的位数为( )(参考数据:)
A.25 B.29 C.27 D.28
7.已知函数,则函数的图象可能是( )
A. B.
C. D.
8.定义一种运算,将函数的图象向左平移个单位,所得图象对应的函数为偶函数,则的最小值是( )
A. B. C. D.
9.如图,函数在一个周期内的图象(不包括端点)与轴,轴的交点分别为,,与过点的直线另相交于,两点,为图象的最高点,为坐标原点,则( )
A. B.
C. D.
10.已知函数若对任意的恒成立,则实数a的取值范围是( )
A. B. C. D.
11.已知在有且仅有个实数根,则实数的取值范围为( )
A. B. C. D.
12.已知函数,当时,恒成立,则实数的取值范围为( )
A. B.
C. D.
二、填空题
13.在中,若,则这个三角形是________.
14.已知曲线y=x2与直线y=kx(k>0)所围成的曲边图形的面积为,则k=________.
15.已知,分别为圆:与:的直径,则的取值范围为________.
16.关于不等式恰有一个整数解,则实数的取值范围是__________.
三、解答题
17.已知函数的定义域为,函数的值域为.
(1)当时,求.
(2)若“”是“”的必要不充分条件,求实数的取值范围.
18.已知向量,,.
(1)若,求的值;
(2)当时,求函数的值域.
19.如图,在平面四边形中,已知,
(1)若平分,且,求的长
(2)若,求的长
20.2020年春节前后,一场突如其来的新冠肺炎疫情在武汉出现并很快地传染开来(已有证据表明2019年10月、11月国外已经存在新冠肺炎病毒),对人类生命形成巨大危害.在中共中央、国务院强有力的组织领导下,全国人民万众一心抗击、防控新冠肺炎,疫情早在3月底已经得到了非常好的控制(累计病亡人数人),然而国外因国家体制、思想观念的不同,防控不力,新冠肺炎疫情越来越严重.疫情期间造成医用防护用品短缺,某厂家生产医用防护用品需投入年固定成本为万元,每生产万件,需另投入成本为.当年产量不足万件时,(万元);当年产量不小于万件时,(万元).通过市场分析,若每件售价为元时,该厂年内生产的商品能全部售完.(利润销售收入总成本)
(1)写出年利润(万元)关于年产量(万件)的函数解析式;
(2)年产量为多少万件时,该厂在这一商品的生产中所获利润最大 并求出利润的最大值.
21.已知函数,其中a为正实数.
(1)若函数在处的切线斜率为2,求a的值;
(2)若函数有两个极值点,,求证:.
22.在直角坐标系中,直线的参数方程为(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为,直线交曲线于两点.
(1)写出直线的极坐标方程和曲线的直角坐标方程;
(2)设点的直角坐标为,若点到两点的距离之积是16,求的值.
23.已知函数.
(1)解不等式;
(2)设函数的最小值为,实数满足,求证:.
期中适应性考试数学(理科)参考答案
1.C 2.D 3.A 4.C 5.D 6.C 7.B 8.C 9.A 10.B 11.B12.D
11、设,
当时,或或.
故方程的正数解由小到大排列为:,,,,,,,…依题意故,故选:B.
12、即,则,则,
令,,
当,,单调递增;
当,,单调递减,
因为,所以,
又,所以恒成立,
故.故选:D.
13.等腰或直角三角形 14.2 15. 16.
15、
.
而
故答案为:
16、①当时,原不等式不成立;
②当时,由恰有一个整数解,得恰有一个整数解.
令,则,因此函数在区间上单调递减,易得不可能只有一个整数解,故不满足;
③当时,由恰有一个整数解,得恰有一个整数解.
由②可知,易得函数在区间上单调递减,在区间上单调递增,故.
又因,且恰有一个整数解,所以,即.
综上,.
故答案为:.
17.(1);(2).
解:(1)由,解得:或,即,
由于,.
当时,,
,.
(2)依题可知,是A的真子集,即 ,
所以,解得:,
所以实数的取值范围为.
18.(1);(2).
(1)因为,,
所以,
因为,所以,所以,所以,
.
(2),因为,所以.
当,即时,取最小值;当,即时,取最大值2.所以当时,函数的值域为.
19.(1)2;(2)5.
解:(1)平分,,
,,在中,,,,
由余弦定理,可得:,解得:,的值为2.
(2),,又,
,
在中,由正弦定理,可得:,即的长为5.
20.(1)当,时,
.
当,时,
.
.
(2)当,时,,
当时,取得最大值(万元)
当,时,
当且仅当,即时等号成立.
即时,取得最大值万元.
综上,所以即生产量为万件时,该厂在这一商品的生产中所获利润最大为万元.
21.(1)1;(2)证明见解析.
解:因为,
所以,
则,所以a的值为
,函数的定义域为,
若,即,则,
此时的单调减区间为;
若,即,则的两根为,
此时的单调减区间为,,
单调增区间为
当时,函数有两个极值点,,且,.
因为
,
要证,只需证
构造函数,则,
在上单调递增,
又,,且在定义域上不间断,
由零点存在定理,可知在上唯一实根,
且在上递减,上递增,所以的最小值为,因为,当时,,所以,
所以恒成立.所以,所以.
22.解:(1)直线的直角坐标方程为,
所以直线的极坐标方程为.
由,得.
所以曲线的直角坐标方程为.
(2)将直线的参数坐标方程代入中,
得.设对应的参数分别为,则.
,或,
23.(1);(2)证明见解析.
(1),即.当时,不等式可化为,解得:
又∵,∴; 当时,不等式可化为,解得:
又∵,∴.当时,不等式可化为,解得:
又∵,∴. 综上所得,或,即.
∴原不等式的解集为.
(2)由绝对值不等式性质得,,
∴,即.
令,则,,
,
等且仅当即时等号成立.
原不等式得证.
同课章节目录
