力的合成

(共44张PPT)
物理：第２章第５节《力的合成》精品课件（教科版必修1）
5.力的合成
1．某同学从学校先向东行走300 m，然后又向南行走400 m到了书店，
那么该同学从学校走到书店的位移是700 m吗？
【答案】　不是．由勾股定理可知从学校走到书店的位移不是700
m，而是500 m.
2．在下图中，一个成年人或两个孩子均能提起相同质量的一桶水，
那么该成年人用的力与两个孩子用的力作用效果是否相同？二者能否等效替换？
【答案】　二者的作用效果均是把一桶水提起，能够等效替换．
一、几个力可用一个力来替代
1．合力、分力
(1)合力与分力：当一个物体受到几个力共同作用时，如果一个力
的 跟这几个力的共同 相同，这一个力叫做那几个力的 ，那几个力叫做这个力的 ．
(2)合力与分力的关系：等效替代关系．
2．力的合成
求几个力的 的过程．
3．共点力
几个力如果都作用在 ，或者它们的作用线 ，这几个力就叫做共点力．
作用效果
效果
分力
合力
合力
相交于同一点
同一点上
俗话说：“三个臭皮匠，顶个诸葛亮．”意为个人的能力是有限的，集体的智慧是无穷的．“众人划桨开大船”说的是众人合力可以排山倒海，可以开动大船．日常生活中一个大人可以搬动一个重物，两个小孩也可以抬动这个重物．如右图．这说明：两个小孩的作用力可以等效为一个大人的作用力．
(1)几个力作用在物体上相当于一个很大力的作用，这是不是就是力的合成？
(2)两个小孩的力可以等效为一个大人的力，在什么条件下可以等效？
(3)两个小孩的力是不是就是这个大人的力，为什么？
【提示】　(1)中所说的几个力的作用效果相当于一个很大的力，这就是力的合成思想；(2)两个小孩的力的作用效果和一个大人的力产生的效果相同，那么两个小孩的力就可以等效为一个大人的力；(3)两个小孩的力产生的效果和一个大人的力相同，但是两个小孩的力和这个大人的力施力物体不同，它们不是同一个力，力的合成时只是说效果相同，一定要注意这种区别．
二、探究共点力合成的规律
实验器材
实验步骤
1．在水平放置的图板上固定一张白纸，将橡皮筋的一端固定在图板上的K点处，橡皮筋的自然长度为 ，如右图．
KE
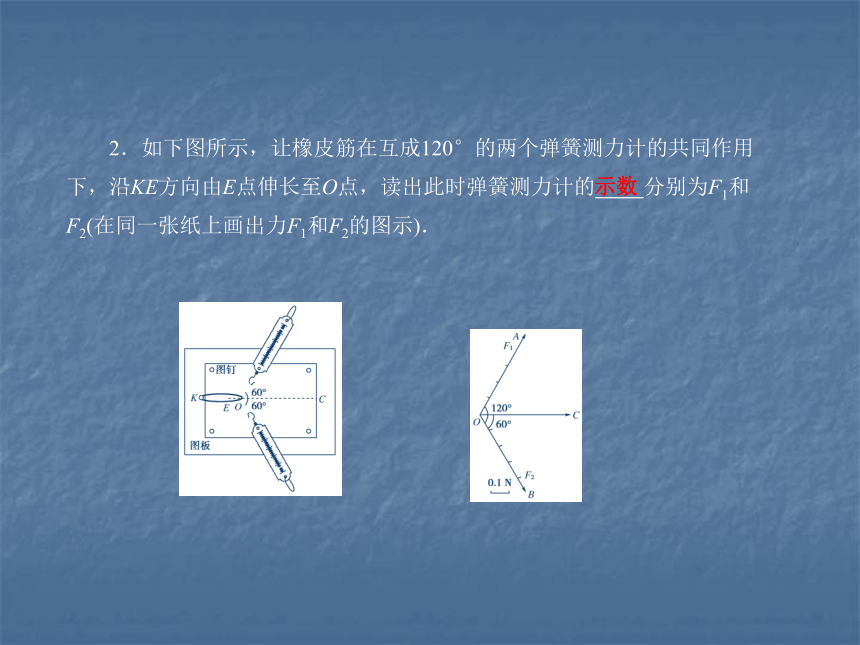
2．如下图所示，让橡皮筋在互成120°的两个弹簧测力计的共同作用下，沿KE方向由E点伸长至O点，读出此时弹簧测力计的 分别为F1和F2(在同一张纸上画出力F1和F2的图示)．
　
示数
3．撤去F1和F2，如下图所示，用一个 直接拉着橡皮筋沿KE伸长到 点，读出此时弹簧测力计的示数为F(在同一张纸上画出力F的图示)．
　
弹簧测力计
O
4．作图分析得出结论
用表示两个共点力F1、F2的线段为 作平行四边形，对角线的 和 与F的大小和方向相同．
5．改变F1和F2的大小和方向，重复上述实验和作图．
邻边
长短
方向
三、互成直角的两个力的合成
1．作图法：从力的作用点起，依两个分力的作用方向按同一 作出两个分力F1和F2，并把F1、F2作为 作出平行四边形，这个平行四边形的对角线的长度按同一标度表示 的大小，对角线的方向就是 的方向，通常可以用量角器直接量出合力F与 的夹角θ.
标度
邻边
合力
合力
某一分力
2．计算法：可以根据平行四边形法则作出示意图，然后由几何知识求解对角线，即为合力．
相互垂直的两个力的合成，如下图所示，F＝
若合力F与分力F1的夹角为θ，则tan θ＝F2/F1.
一、合力与分力的关系
1．正确理解合力与分力
(1)合力与几个分力间是等效替代关系，受力分析时，分力与合力不能同时作为物体所受的力．
(2)只有同一物体同时受到的力才能合成．
2．合力与分力间的大小关系
(1)两力同向时合力最大：F＝F1＋F2，方向与两力同向；
(2)两力方向相反时，合力最小：F＝|F1－F2|，方向与两力中较大的力同向；
(3)两力成某一角度θ时，如右图所示，三角形AOC的每一条边对应一个力，由几何知识可知：两边之和大于第三边，两边之差小于第三边，即|F1－F2||F1－F2|≤F≤F1＋F2.
(4)夹角θ越大，合力就越小．
(5)合力可以大于等于两分力中的任何一个力，也可以小于等于两分力中的任何一个力．
1)力的合成是唯一的；
(2)只有同一物体所受的力才能合成；
(3)不同性质的力也可以合成，因为合力与分力是作用效果上的一种等效代替．在实际研究几个力的合力时，常采用平行四边形定则，通过作图法或解析法求出合力．
(
1.下列关于合力与分力之间的关系的说法正确的是(　　)
A．合力就是分力的代数和
B．合力总比某一分力大
C．分力与合力的方向总是不一致的
D．合力的大小可能等于某一分力的大小
【解析】　合力是分力的矢量和，而不是代数和，所以A项错误；合力的大小介于两分力代数和与两分力代数差的绝对值之间，因此B项错误，D项正确；当两分力方向相同时，合力与分力方向相同，C项错误．
【答案】　D
二、共点力合成的平行四边形定则
1．同一直线上两个力的合成法则
同一直线上的两个共点力F1、F2，两者同方向时，其合力大小为F1＋F2，方向为两个力的方向．两者反方向时，其合力大小为|F1－F2|，方向为F1和F2中较大的方向．
2．不在同一直线上两个力的合成法则——平行四边形定则
(1)两个力合成时，以表示这两个力的线段为邻边作平行四边形，这两个邻边之间的对角线表示合力的大小和方向．
(2)两个以上的力的合成方法：先求出任意两个力的合力，再求出这个合力与第三个力的合力，直到把所有 都合成进去，最后得到的结果就是这些力的合力．
外力
(3)求几种特殊情况的合力
①夹角为θ、两个等大的力的合成，如图甲所示，作出的平行四边形为菱形，利用其对角线互相垂直的特点可得到直角三角形，解直角三角形求得合力F′＝2Fcos ，合力F′与每一个分力的夹角等于θ/2，特殊情况：夹角为120°的两个等大的力的合成，如图乙所示，实际上是图甲的特殊情况：F′＝2F·cos ＝F，即合力大小等于分力．实际上对角线把画出的菱形分为两个等边三角形，所以合力与分力等大．
推论：当F1＝F2＝F3，且三力夹角两两为120°时，其合力F＝0.
甲
②合力F与一个分力F1互相垂直时的力的合成，如图丙所示，利用对角线与一个分力垂直得到直角三角形，解直角三角形可求得合力
F＝ ，合力F与F1的夹角为90°.
以上三种特殊的合成在今后的学习中会经常遇到，应该熟练掌握．
2.两个大小恒定的共点力，合力的最大值为a，合力的最小值为b.当两个共点力互相垂直时，合力大小为(　　)
A．a＋b　　　　　　　B.
C. D.
【解析】　设两力大小分别为F1、F2，且F1>F2，
则F1＋F2＝a，F1－F2＝b.
两力垂直时合力F＝ ，
联立得F＝.
【答案】　D
大小分别为5 N、7 N、9 N的三个力合成，其合力F大小的范围为(　　)
A．3 N≤F≤20 N　　　　　B．2 N≤F≤21 N
C．0≤F≤20 N D．0≤F≤21 N
【解析】　求三个力的合力大小的范围，则先确定两个力合力的大小范围，由平行四边形定则，5 N和7 N的合力最大为12 N，最小为2 N，则这个合力大小可能为9 N，而若它的方向与9 N的方向相反，这两个力合成后的合力可能为0，若它的大小为12 N，且方向与9 N力的方向相同时，合力的大小可能是21 N，故正确答案为D.
【答案】　D
(1)F1、F2两力合力大小的取值范围为|F1－F2|≤F≤F1＋F2.
(2)多个力合成时，先求出任意两个力的合力，再求出这个合力与第三个力的合力，直到把所有的力都合成进去，最后得到的结果就是这些力的合力．
1－1：如右图所示，有两个共点力，一个是
F1＝40 N，一个是F2，它们的合力是F＝100 N，则F2的大小可能是(　　)
A．20 N　　 　B．40 N
C．80 N D．160 N
【解析】　两个共点力的合力大小的取值范围是
|F1－F2|≤F≤F1＋F2.根据以上关系，可以求得F2大小的取值范围是60 N≤F2≤140 N．故只有选项C正确．
【答案】　C
如下图甲所示，物体受到大小相等的两个拉力的作用，每个拉力都是2 000 N，夹角为50°.请分别用力的图示法和计算法求出这两个拉力的合力(cos 25°＝0.906)．
【解析】　解法一：作图法：按作图法取0.5 cm长表示500 N的力，O点表示力的作用点，作出平行四边形，如图乙所示，量出对角线长为3.6 cm，故合力F的大小为 ×500 N＝3 600 N，合力的方向沿两分力F1和F2的夹角的平分线．
解法二：计算法：如图丙所示，直角三角形OAD中，OD表示合力F的一半，∠AOD＝25°，由直角三角形知识得F/2＝F1cos 25°，
则F＝2F1cos 25°≈2×2 000×0.906 N≈3624 N.
合力F的方向与F1的方向的夹角θ＝25°，如图丙所示．
(1)求解矢量时要注意不仅要求出其大小，还要求出其方向．其方向经常用它与已知矢量的夹角表示．(2)比较两种解法：分析可知应用计算法求解较为精确，作图法的精确度相对差些，但在测量误差允许范围内，所得的结果还是一致的．(3)用作图法求合力时，要采用统一的标度，要标出箭头且实线、虚线要分明．
大小均为10 N的两个共点力，当其夹角为120°时，合力的大小为多少？若再增加一个大小为12 N的力，三个力共点且在一个平面内，并且互成120°角，则这三个力的合力大小为多少？
　
我们可依据题给条件作出平行四边形，如右图所示，由示意图可看出每一个力与合力间的夹角为
60°，根据几何知识可知，代表合力F的线段与代表F1、F2的线段长度是相等的，因此合力大小应为10 N．当再加一个12 N的力，且与F1、F2夹角均为120 °时，由图分析可知，这个力应与F1、F2的合力F在一条直线上，且方向相反，故可将三个力的合力看成是12 N的力与力F合成的结果，即三个力的合力大小为2 N.
【解析】　
在求几个力的合成时，依据题意作出平行四边形，根据几何关系解决问题是基本的思路和方法．
3－1：如右图所示，六个力的合力为________N．若去掉1 N的那个力，则其余五个力的合力为____________N，合力的方向是________．
【解析】　因为这六个力中，各有三对力方向相反，故先将任意两个方向相反的力合成，然后再求合力．
由图可以看出，任意两个方向相反的力的合力都为3 N，且互成120°，所以这六个力的合力为零．
因为这六个力的合力为零，所以，任意五个力的合力一定与第六个力大小相等，方向相反．由此得，去掉1 N的那个力后，其余五个力的合力为1 N，方向与1 N的力的方向相反．
【答案】　0　1 N　与1 N的力的方向相反
对力的合成法则理解不深入导致错误
共点的两个力(F1、F2)的合力的取值范围是|F1－F2|≤F合≤F1＋F2.若第三个共点力的大小在这一范围内，那么这三个力的合力可以为零．必须指出，矢量的正负号是用来表示矢量的方向的，比较两个矢量的大小应比较这两个矢量的绝对值，而不应比较这两个力的代数值．
大小为4 N、7 N和9 N的三个共点力，它们的最大合力是多大？最小合力是多大？
【错解】　当三个力同方向时，合力最大，此时，F合＝20 N．
当4 N、7 N的两个力同向且与9 N的力方向相反时，合力最小，此时F合＝2 N.
【正解】　当三个力同方向时，合力最大，合力最大值为F＝F1＋F2＋F3＝20 N.
由于这三个力中任意两个力的合力的代数差(即最小值)都小于第三个力，所以这三个力的合力的最小值为零．
【错因分析】　在错解中，求三个共点力的最小合力时，由于思维定势的副作用，仍和求最大合力一样，把三个力限定在一条直线上考虑，从而导致错误．
1．下列关于合力和分力之间的关系的说法中正确的是(　　)
A．合力就是分力的代数和
B．合力总比某一分力大
C．分力与合力的方向总是不一致的
D．合力的大小可能等于某一分力的大小
【解析】　合力是分力的矢量和，而不是代数和，A错误；合力的大小在两分力的代数和与两分力代数差的绝对值之间，B错误，D正确；当两分力方向相同时，合力与分力方向相同，C错误．故正确答案为D.
【答案】　D
2．两个大小相等的共点力F1、F2，当它们间的夹角为90°时，
合力大小为20 N，那么当它们之间的夹角为120°时，合力的大小为(　　)
A．40 N B．10 N
C．20 N D．10 N
【解析】　设F1＝F2＝F.当它们的夹角α＝90°时，其合力为 F，
即 F＝20 N，F＝10 N．当夹角为120°时，其合力与F等大．故选B.
【答案】　B
3．一个重为20 N的物体置于光滑的水平面上，当用一个F＝5 N的力竖直向上拉该物体时，如右图所示，物体受到的合力为(　　)
A．15 N　　　　B．25 N
C．20 N D．0
【解析】　由于物体的重力大于拉力，则地面对物体有支持力，且物体仍然静止．因为物体静止，所以竖直向上的拉力和支持力的合力与重力的合力为零．故只有选项D正确．
【答案】　D
4.
设有三个力同时作用在质点P上，它们的大小和方向相当于正六边形的两条边和一条对角线，如右图所示，这三个力中最小的力的大小为F，则这三个力的合力等于(　　)
A．3F B．4F
C．5F D．6F
【解析】　由图可知F1＝F2＝F，F3＝2F.其中F1、F2成120°角，则这两个力的合力等于F，方向在其角平分线上，即与F3同向，故这三个力的合力等于3F.
【答案】　A
5．把一个物体放在倾角为37°的斜面上，物体处于静止状态，已知物体受到斜面的支持力为40 N，受到斜面的摩擦力为30 N，求这两个力的合力．
【解析】　
用F1表示支持力，F2表示摩擦力，并作出力的示意图，因为支持力与摩擦力垂直，所以力的平行四边形为矩形，由勾股定理得：
【答案】　合力的大小为50 N，方向竖直向上