4.1正弦和余弦同步练习-2020-2021学年湘教版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 4.1正弦和余弦同步练习-2020-2021学年湘教版数学九年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 590.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 12:15:17 | ||
图片预览



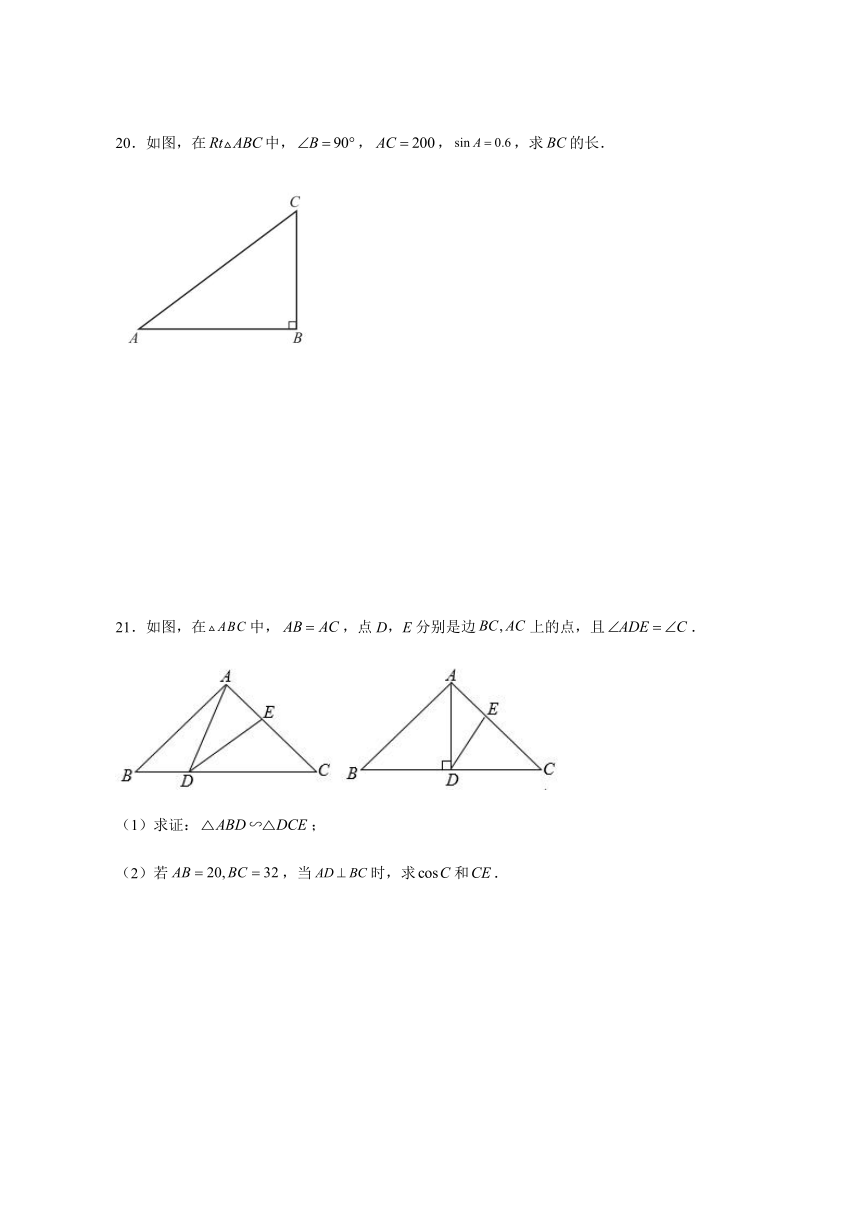
文档简介
正弦和余弦
一、单选题
1.在直角中,,,,则的为( )
A. B. C. D.
2.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=,AB=4,则AD的长为( )
A.4 B. C. D.
3.在中,,,,则的值为( )
A. B. C. D.
4.若cosA,则锐角∠A为( )
A.30° B.15° C.45° D.60°
5.在中,,若的三边都缩小5倍,则的值( )
A.放大5倍 B.缩小5倍 C.不变 D.无法确定
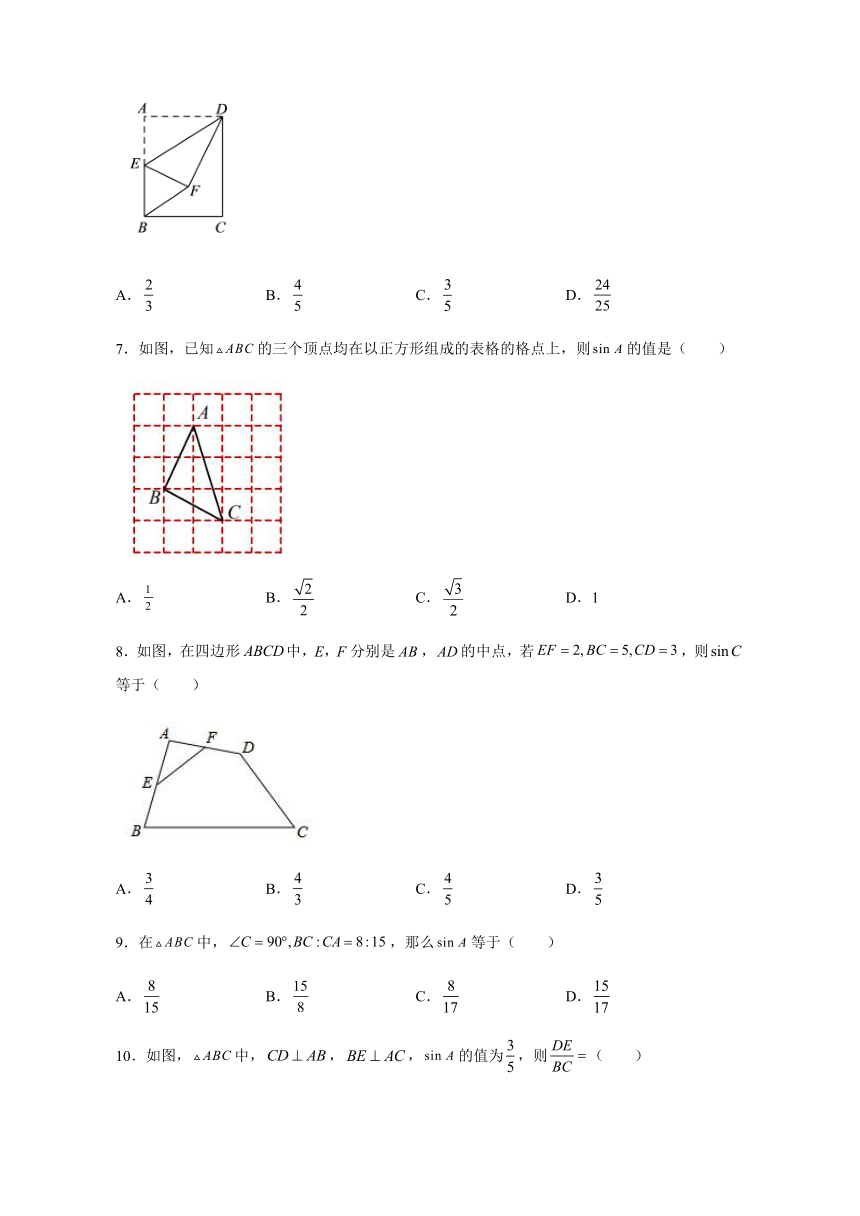
6.如图,四边形为矩形,点为边一点,将沿折叠,点落在矩形内的点处,连接,且,的正弦值为,则的值为( )
A. B. C. D.
7.如图,已知的三个顶点均在以正方形组成的表格的格点上,则的值是( )
A. B. C. D.1
8.如图,在四边形中,E,F分别是,的中点,若,则等于( )
A. B. C. D.
9.在中,,那么等于( )
A. B. C. D.
10.如图,中,,,的值为,则( )
A. B. C. D.
11.在中,分别是的对边,如果,那么等于( ).
A. B. C. D.
12.当锐角的时,的值为( )
A.小于 B.小于 C.大于 D.大于
二、填空题
13.若∠A是锐角,且cosA=,则(90°﹣A)=_____.
14.如图,在中,,,,点是斜边上的动点且不与,重合,连接,点与点关于直线对称,连接,当垂直于的直角边时,的长为__.
15.如图,在矩形中,,,点是的中点,连接,将沿折叠,点落在点处,连接,则__________.
16.已知:如图,中,的面积等于9,则______.
17.如图,△ABC的顶点都在正方形网格的格点上,则sin∠ACB的值为 __________________.
三、解答题
18.在中,是边上的高,,求和.如果呢?
19.在中,,,,求的周长和面积.
20.如图,在中,,,,求的长.
21.如图,在中,,点D,E分别是边上的点,且.
(1)求证:;
(2)若,当时,求和.
22.如图在等腰三角形ABC中,AB=AC,点D、E分别是AB、BC的中点,过点B作BF⊥AC于点F,BF与DE交于点G.
(1)求证:DE⊥BF;
(2)连结EF,若S△CEF=S△BDG,求cos∠CEF的值.
参考答案
1.A
解:在Rt△ABC中,∵∠C=90°,AB=3,,
∴,
∴sinA=,
故选:A.
2.C
解:在矩形ABCD中,AB=CD=4,,
∴,
∵DE⊥AC,
∴,
∴,
∴∠ADE=∠ECD=α.
在Rt△DEC中,cos∠ECD=cosα=,
即,
∴CE=.
根据勾股定理得DE=.
在Rt△AED中,cosα=,
即,
∴AD=.
故选:C.
3.A
解:由勾股定理得,,
则,
故选:A.
4.C
解:由cosA,则锐角∠A为45°,
故选:C.
5.C
解:∵∠C=90°,
∴sinA=∠A的对边与斜边的比,
∵△ABC的三边都缩小5倍,
∴∠A的对边与斜边的比不变,
∴sinA的值不变.
故选:C.
6.A
解:如图,过点F作FP⊥AB于点P
由折叠的性质可得:AE=EF,∠AED=∠FED
∵BE=EF
∴BE=AE=EF,∠EFB=∠EBF
∵∠BEF+2∠AED=∠BEF+2∠EBF=180゜
∴∠AED=∠EBF
∵四边形ABCD为矩形,PF⊥AB
∴∠A=∠FPB=90゜
∴△ADE∽△PFB
∴
∵在中,
∴设EF=25a,则PF=24a
由勾股定理求得
∴BP=BE-PE=18a
∴
∴
∴
故选:A.
7.B
解:设每个小正方形的边长为1,由网格构造直角三角形可得,AC2=12+32=10,AB2=12+22=5,BC2=12+22=5,
∵AB2=AC2+BC2,
∴△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴sinA=sin45°=.
故选:B.
8.C
解:连接,
∵E,F分别是的中点,
∴,
∵,
∴,
又∵,
∴,
∴△BCD是直角三角形,,
∴.
故选:C.
9.C
解:在中,,
设,则,
则,
根据正弦的定义可得.
故选C
10.D
解:,,
,
,
,
,
,
,
,
,
设,则,
,
.
故选D.
11.A
解:如图,在Rt△ABC中,,
∵,
∴,
∴ ,
即.
故选:A
12.A
解:根据cos45°=,余弦函数随角增大而减小,则∠A一定小于45°.
故选:A.
13.
解:如图,在中,cosA==,
故答案为:.
14.1或3
解:,,∠C=90°
,
,
①如图1中,当时,设直线交于,
由轴对称的性质可知,直线平分,
∴平分,
,
∵AC⊥BC,,
,
,
,
;
②当于时,同法可证,
综上所述,满足条件的的值为1或3.
故答案为:1或3.
15.
解:过作于,
由折叠的性质得:,,
点是的中点,,
,
,
又∵,
,,
∵,
,
∵,
,
,
∵,,,
∴,
,
故答案为:.
16.
解:过C作CD⊥AB于D,
∵△ABC中,AB=9,△ABC的面积等于9,
∴ ×AB×CD=9,
∴CD=2,
∴sinB= .
故答案为:.
17.
解:作如图所示的辅助线,则BD⊥AC,
∵BC=,BD=,
∴sin∠ACB=,
故答案为:.
18.,;,
解:如图,当是边上的高,,
;
如图,当时,
同理可得:
19.的周长为60,面积为150
解:如图,,,,
解得: 经检验:符合题意;
20.120
解:在中,
∵,
即,
∴.
21.(1)证明见详解;(2)cosC=,.
解:证明:(1)∵AB=AC,
∴∠ABC=∠ACB.
∵∠ADC=∠ABC+∠BAD,
∴∠ADE+∠EDC=∠ABC+∠BAD,且∠ADE=∠B,
∴∠EDC=∠BAD且∠ABD=∠DCE,
∴.
解:(2)∵AB=AC=20,,AD⊥BC,
∴BD=CD=BC=16,
在Rt△ADC中,cosC=,
∵,∠DAC+∠C=90°,
∴∠DAC+∠ADE=90°,
∴∠AED=180°-(∠DAC+∠ADE)=90°,
在Rt△CDE中,cosC=
∴.
22.(1)见解析;(2)
解:(1)∵点D、E分别是AB、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
∴∠DGB=∠AFB.
∵BF⊥AC,
∴∠AFB=∠BFC=90°.
∴∠DGB=90°,
∴DE⊥BF.
(2)∵∠BFC=90°,点E是BC的中点,
∴EF=BE=EC,
∴∠EFC=∠C.
∵AB=AC,
∴∠ABC=∠C.
∴∠CEF=180°﹣2∠C=∠BAC.
∵,点D是AB的中点,
∴△BDG∽△BAF,
∴
∵点E是BC的中点,
∴S△BFC=2S△CEF,
∵S△CEF=,
∴.
∴S△ABC=S△ABF+S△BCF=S△ABF+2S△CEF=S△CEF.
∴==.
在中,.
一、单选题
1.在直角中,,,,则的为( )
A. B. C. D.
2.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=,AB=4,则AD的长为( )
A.4 B. C. D.
3.在中,,,,则的值为( )
A. B. C. D.
4.若cosA,则锐角∠A为( )
A.30° B.15° C.45° D.60°
5.在中,,若的三边都缩小5倍,则的值( )
A.放大5倍 B.缩小5倍 C.不变 D.无法确定
6.如图,四边形为矩形,点为边一点,将沿折叠,点落在矩形内的点处,连接,且,的正弦值为,则的值为( )
A. B. C. D.
7.如图,已知的三个顶点均在以正方形组成的表格的格点上,则的值是( )
A. B. C. D.1
8.如图,在四边形中,E,F分别是,的中点,若,则等于( )
A. B. C. D.
9.在中,,那么等于( )
A. B. C. D.
10.如图,中,,,的值为,则( )
A. B. C. D.
11.在中,分别是的对边,如果,那么等于( ).
A. B. C. D.
12.当锐角的时,的值为( )
A.小于 B.小于 C.大于 D.大于
二、填空题
13.若∠A是锐角,且cosA=,则(90°﹣A)=_____.
14.如图,在中,,,,点是斜边上的动点且不与,重合,连接,点与点关于直线对称,连接,当垂直于的直角边时,的长为__.
15.如图,在矩形中,,,点是的中点,连接,将沿折叠,点落在点处,连接,则__________.
16.已知:如图,中,的面积等于9,则______.
17.如图,△ABC的顶点都在正方形网格的格点上,则sin∠ACB的值为 __________________.
三、解答题
18.在中,是边上的高,,求和.如果呢?
19.在中,,,,求的周长和面积.
20.如图,在中,,,,求的长.
21.如图,在中,,点D,E分别是边上的点,且.
(1)求证:;
(2)若,当时,求和.
22.如图在等腰三角形ABC中,AB=AC,点D、E分别是AB、BC的中点,过点B作BF⊥AC于点F,BF与DE交于点G.
(1)求证:DE⊥BF;
(2)连结EF,若S△CEF=S△BDG,求cos∠CEF的值.
参考答案
1.A
解:在Rt△ABC中,∵∠C=90°,AB=3,,
∴,
∴sinA=,
故选:A.
2.C
解:在矩形ABCD中,AB=CD=4,,
∴,
∵DE⊥AC,
∴,
∴,
∴∠ADE=∠ECD=α.
在Rt△DEC中,cos∠ECD=cosα=,
即,
∴CE=.
根据勾股定理得DE=.
在Rt△AED中,cosα=,
即,
∴AD=.
故选:C.
3.A
解:由勾股定理得,,
则,
故选:A.
4.C
解:由cosA,则锐角∠A为45°,
故选:C.
5.C
解:∵∠C=90°,
∴sinA=∠A的对边与斜边的比,
∵△ABC的三边都缩小5倍,
∴∠A的对边与斜边的比不变,
∴sinA的值不变.
故选:C.
6.A
解:如图,过点F作FP⊥AB于点P
由折叠的性质可得:AE=EF,∠AED=∠FED
∵BE=EF
∴BE=AE=EF,∠EFB=∠EBF
∵∠BEF+2∠AED=∠BEF+2∠EBF=180゜
∴∠AED=∠EBF
∵四边形ABCD为矩形,PF⊥AB
∴∠A=∠FPB=90゜
∴△ADE∽△PFB
∴
∵在中,
∴设EF=25a,则PF=24a
由勾股定理求得
∴BP=BE-PE=18a
∴
∴
∴
故选:A.
7.B
解:设每个小正方形的边长为1,由网格构造直角三角形可得,AC2=12+32=10,AB2=12+22=5,BC2=12+22=5,
∵AB2=AC2+BC2,
∴△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴sinA=sin45°=.
故选:B.
8.C
解:连接,
∵E,F分别是的中点,
∴,
∵,
∴,
又∵,
∴,
∴△BCD是直角三角形,,
∴.
故选:C.
9.C
解:在中,,
设,则,
则,
根据正弦的定义可得.
故选C
10.D
解:,,
,
,
,
,
,
,
,
,
设,则,
,
.
故选D.
11.A
解:如图,在Rt△ABC中,,
∵,
∴,
∴ ,
即.
故选:A
12.A
解:根据cos45°=,余弦函数随角增大而减小,则∠A一定小于45°.
故选:A.
13.
解:如图,在中,cosA==,
故答案为:.
14.1或3
解:,,∠C=90°
,
,
①如图1中,当时,设直线交于,
由轴对称的性质可知,直线平分,
∴平分,
,
∵AC⊥BC,,
,
,
,
;
②当于时,同法可证,
综上所述,满足条件的的值为1或3.
故答案为:1或3.
15.
解:过作于,
由折叠的性质得:,,
点是的中点,,
,
,
又∵,
,,
∵,
,
∵,
,
,
∵,,,
∴,
,
故答案为:.
16.
解:过C作CD⊥AB于D,
∵△ABC中,AB=9,△ABC的面积等于9,
∴ ×AB×CD=9,
∴CD=2,
∴sinB= .
故答案为:.
17.
解:作如图所示的辅助线,则BD⊥AC,
∵BC=,BD=,
∴sin∠ACB=,
故答案为:.
18.,;,
解:如图,当是边上的高,,
;
如图,当时,
同理可得:
19.的周长为60,面积为150
解:如图,,,,
解得: 经检验:符合题意;
20.120
解:在中,
∵,
即,
∴.
21.(1)证明见详解;(2)cosC=,.
解:证明:(1)∵AB=AC,
∴∠ABC=∠ACB.
∵∠ADC=∠ABC+∠BAD,
∴∠ADE+∠EDC=∠ABC+∠BAD,且∠ADE=∠B,
∴∠EDC=∠BAD且∠ABD=∠DCE,
∴.
解:(2)∵AB=AC=20,,AD⊥BC,
∴BD=CD=BC=16,
在Rt△ADC中,cosC=,
∵,∠DAC+∠C=90°,
∴∠DAC+∠ADE=90°,
∴∠AED=180°-(∠DAC+∠ADE)=90°,
在Rt△CDE中,cosC=
∴.
22.(1)见解析;(2)
解:(1)∵点D、E分别是AB、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
∴∠DGB=∠AFB.
∵BF⊥AC,
∴∠AFB=∠BFC=90°.
∴∠DGB=90°,
∴DE⊥BF.
(2)∵∠BFC=90°,点E是BC的中点,
∴EF=BE=EC,
∴∠EFC=∠C.
∵AB=AC,
∴∠ABC=∠C.
∴∠CEF=180°﹣2∠C=∠BAC.
∵,点D是AB的中点,
∴△BDG∽△BAF,
∴
∵点E是BC的中点,
∴S△BFC=2S△CEF,
∵S△CEF=,
∴.
∴S△ABC=S△ABF+S△BCF=S△ABF+2S△CEF=S△CEF.
∴==.
在中,.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
