4.4解直角三角形的应用 同步练习 2020-2021学年湘教版九年级数学上册(word版含解析)
文档属性
| 名称 | 4.4解直角三角形的应用 同步练习 2020-2021学年湘教版九年级数学上册(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 663.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 18:04:48 | ||
图片预览



文档简介
解直角三角形的应用
一、单选题
1.河堤横断面如图所示,堤高米,迎水坡的坡比为,则AB的长为( )
A.米 B.米 C.18米 D.21米
2.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i =1:0.75,坡长BC=25米,则此时AB 的长约为( )(参考数据:sin40°≈ 0.64,cos40° ≈ 0.77,tan40°≈ 0.84)
A.10.4 米 B.12.4 米 C.27.4 米 D.22.4 米
3.知识改变世界,科技改变生活,导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C地表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地,导航显示车辆应沿北偏东方向行驶至B地,再沿北偏西方向行驶一段距离才能到达C地,则B,C两地的距离为( ).(结果保留根号,参考数据:,,)
A. B. C. D.
4.重庆朝天门码头位于重庆市渝中半岛的嘉陵江与长江交汇处,是重庆最古老的码头.如图,小王在码头某点E处测得朝天门广场上的某高楼AB的顶端A的仰角为45°,接着他沿着坡度为1:2.4的斜坡EC走了26米到达坡顶C处,到C处后继续朝高楼AB的方向前行18米到D处,在D处测得A的仰角为74°,则此时小王距高楼的距离BD为( )米.(结果精确到1米,参考数据:sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
A.12 B.13 C.15 D.16
5.如图,为了测量某建筑物BC的高度,某数学兴趣小组采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,先沿斜坡AD行走390米至坡顶D处,再从D处沿水平方向继续前行一定距离后至点E处,在E点处测得该建筑物顶端C的仰角为68°,建筑物底端B的俯角为57°,其中A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4,根据数学兴趣小组的测量数据,计算得出建筑物BC的高度约为( )(计算结果精确到0.1米,参考数据:sin68°≈0.93,tan68°≈2.48,sin57°≈0.84,tan57°≈1.54)
A.241.6米 B.391.6米 C.422.9米 D.572.9米
6.图1是某公园的一个滑梯,图2是其示意图.滑梯的高BC为2m,坡角∠A为60°,由于滑梯坡角过大存在安全隐忠,公园管理局决定对滑梯进行整改,要在高度不变的前提下,通过加长滑梯的水平距离AB,使得坡角∠A满足30°≤∠A≤45°,则AB加长的距离可以是( )
(参考数据:≈1.414,≈1.732)
A.0.8m B.1.6m C.2.4m D.3.2m
7.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.米 B.米 C.米 D.米
8.如图是一架人字梯,已知米,AC与地面BC的夹角为,则两梯脚之间的距离BC为( )
A.米 B.米 C.米 D.米
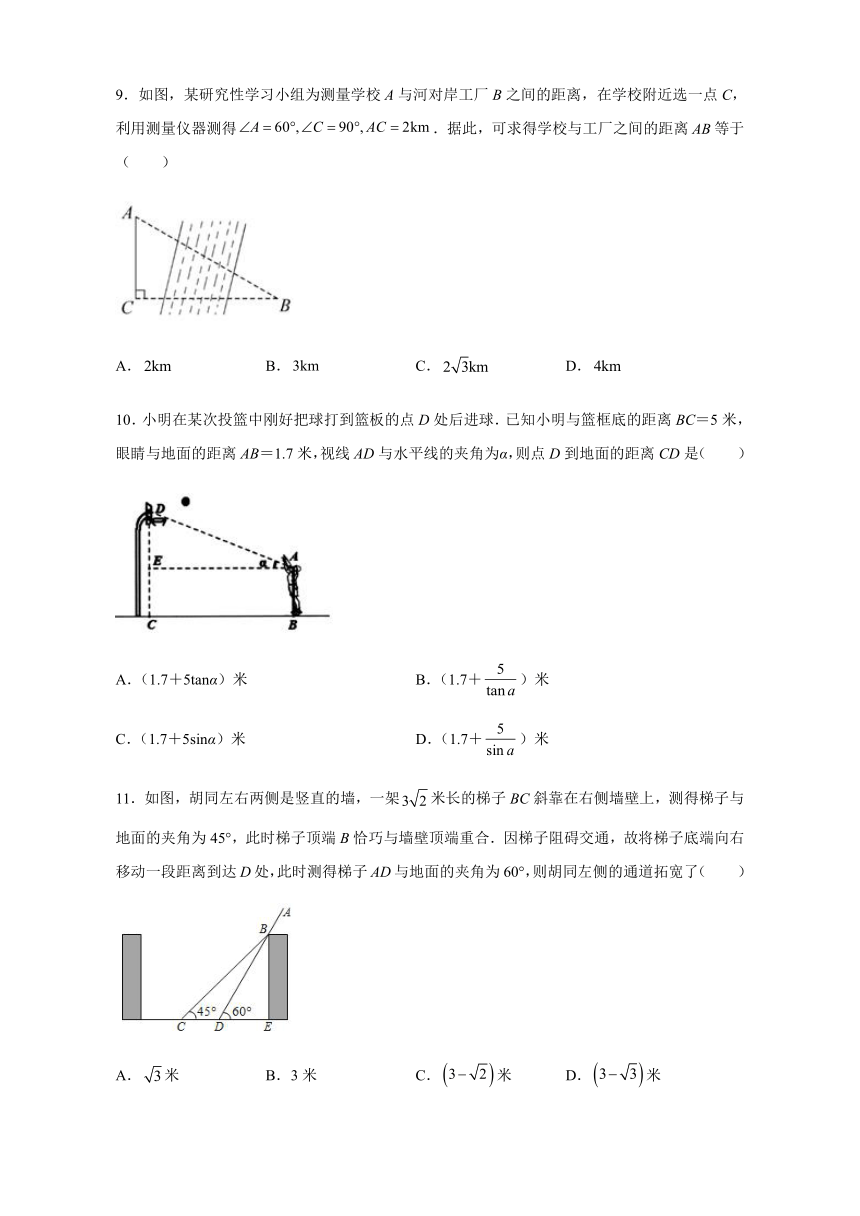
9.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得.据此,可求得学校与工厂之间的距离等于( )
A. B. C. D.
10.小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为α,则点D到地面的距离CD是( )
A.(1.7+5tanα)米 B.(1.7+)米
C.(1.7+5sinα)米 D.(1.7+)米
11.如图,胡同左右两侧是竖直的墙,一架米长的梯子BC斜靠在右侧墙壁上,测得梯子与地面的夹角为45°,此时梯子顶端B恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达D处,此时测得梯子AD与地面的夹角为60°,则胡同左侧的通道拓宽了( )
A.米 B.3米 C.米 D.米
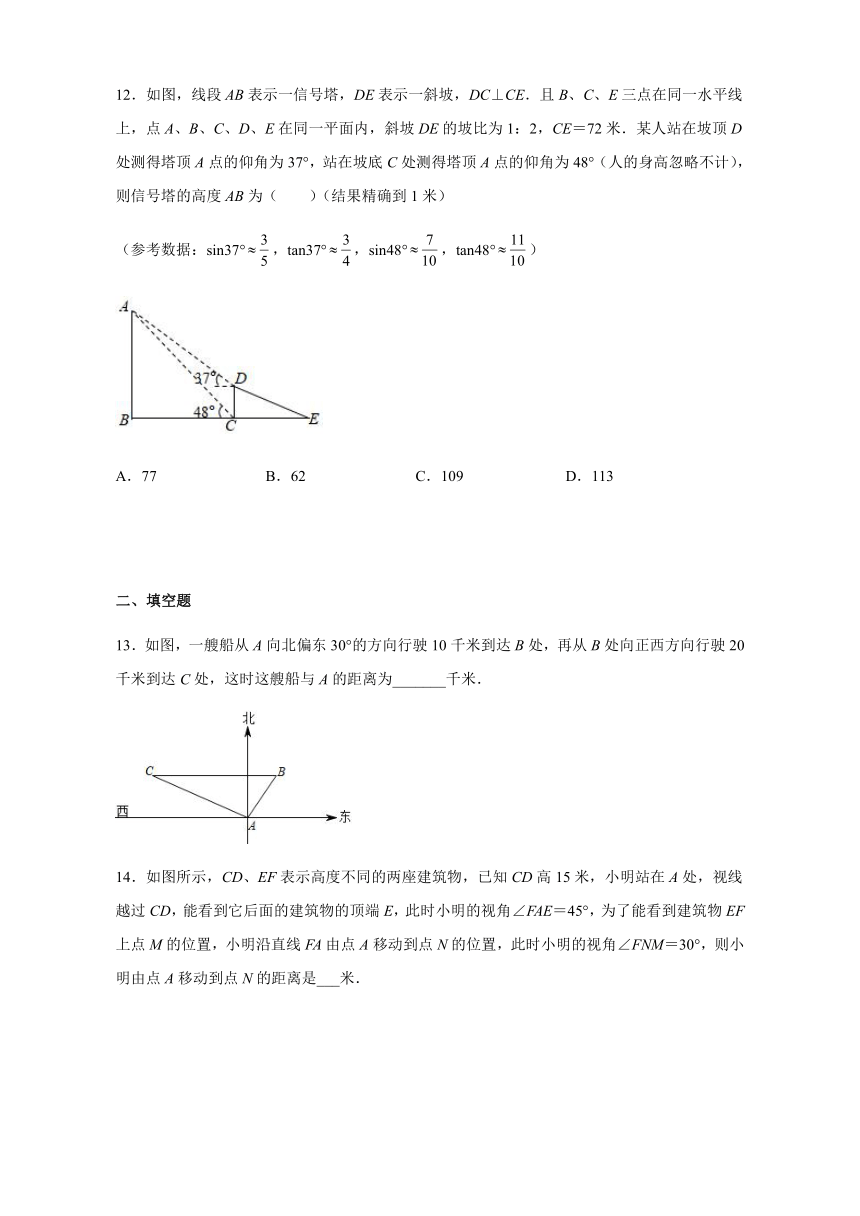
12.如图,线段AB表示一信号塔,DE表示一斜坡,DC⊥CE.且B、C、E三点在同一水平线上,点A、B、C、D、E在同一平面内,斜坡DE的坡比为1:2,CE=72米.某人站在坡顶D处测得塔顶A点的仰角为37°,站在坡底C处测得塔顶A点的仰角为48°(人的身高忽略不计),则信号塔的高度AB为( )(结果精确到1米)
(参考数据:sin37°,tan37°,sin48°,tan48°)
A.77 B.62 C.109 D.113
二、填空题
13.如图,一艘船从A向北偏东30°的方向行驶10千米到达B处,再从B处向正西方向行驶20千米到达C处,这时这艘船与A的距离为_______千米.
14.如图所示,CD、EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明沿直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,则小明由点A移动到点N的距离是___米.
15.如图,小石同学在A,B两点分别测得某建筑物上条幅两端C,D两点的仰角均为60°,若点O,A,B在同一直线上,A,B两点间距离为3米,则条幅的高CD为______米.
16.如图,新疆部A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,某同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时这位同学一共走的距离为______米.
17.一颗珍贵的百年老树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,做法如下:在地面上选取一点,测得,米,,则这棵树的高约为________米.(结果精确到0.1,参考数据:,,)
三、解答题
18.如图,三条笔直公路两两相交,交点分别为A,B,C,测得∠CAB=30°,∠ABC=45°,AC=8千米,求A,B两点间的距离.(结果保留根号)
19.如图,某人从山脚下的点A走了后到达山顶的点B,已知点B到山脚的垂直距离为,求山的坡度(,结果精确到0.001).
20.如图,一艘货轮以的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B.货轮继续向北航行后到达C处,发现灯塔B在它北偏东方向,求此时货轮与灯塔B的距离(结果精确到).
21.如图,燕尾槽的横截面是梯形,其中,燕尾角,外口宽,燕尾槽深度是,求它的里口宽(结果精确到; sin55°=0.82,cos55°=0.57,tan55°=1.43).
22.如图1是某工厂生产的某种多功能儿童车,根据需要可变形为滑板车或三轮车,图2,图3是其示意图,已知前后车轮半径相同,车杆AB的长为60cm,点D是AB的中点,前支撑板DE=30cm,后支撑板EC=40cm,车杆AB与BC所成的∠ABC=53°.(参考数据:)
(1)如图2,当支撑点E在水平线BC上时,求支撑点E与前轮轴心B之间的距离BE的长;
(2)如图3,当座板DE与地平面保持平行时,问变形前后两轴心BC的长度有没有发生变化?若不变,请通过计算说明;若变化,请求出变化量.
参考答案
1.C
解:∵BC=9米,迎水坡AB的坡比为1:,
∴,
解得,AC=9,
∴AB==18,
故选:C.
2.A
解:如图,延长交延长线于点,作于点,
,
,
四边形为矩形,
,,
,
设、,
由可得,,
解得:或(舍去),
则,,
,
在中,,
,
故选:A.
3.C
解:如图所示,作BD⊥AC于D点,则∠ADB=∠CDB=90°,
则由题意可知,∠A=60°,∠ABD=30°,∠CBD=53°,
在Rt△ABD中,设,则,
∴,
在Rt△CBD中,,
即:,
解得:,
经检验,是上述分式方程的解,
∴,
∵,
∴,
即:,
故选:C.
4.B
解:过E作EH⊥AB交AB的延长线于H,
过C作CG⊥EH于G,
则CG=BH,BC=GH,
∵CE=26,=1:2.4,
∴CG=10,EG=24,
∴BH=CG=10,
设BD=x,
在Rt△ABD中,
∵∠ADB=74°,
∴AB=tan74° x≈3.49x,
∴AH=AB+BH=3.49x+10,
∵EH=EG+GH=24+18+x,
∵∠AEH=45°,
∴AH=EH,
∴3.49x+10=24+18+x,
解得:x≈13,
∴BD=13(米),
答:小王距高楼的距离BD为13米.
故选:B.
5.B
解:如图作DH⊥AB于H,延长DE交BC于F.
在Rt△ADH中,AD=390米,DH:AH=1:2.4,
∴DH=150(米),
∵四边形DHBF是矩形,
∴BF=DH=150米,
在Rt△EFB中,tan57°=,
∴EF=,
在Rt△EFC中,FC=EF tan68°,
∴CF≈×2.48≈241.6(米),
∴BC=BF+CF=391.6米.
故选:B.
6.B
解:如图,在Rt△ABC,∠CAB=60°,BC=2,
∴AB===,
当坡角为45°时,有BD=BC=2,
∴DA=2﹣AB=2﹣≈0.85(m),
当坡角为30°时,有BE==(m),
∴EA=BE﹣AB=2﹣≈2.31(m),
当坡角满足30°≤∠A≤45°,
∴AB加长的距离x的取值范围为0.85≤x≤2.31,
故选:B.
7.A
解:在Rt△ABC中,
,
即,
故选:A.
8.A
解:过点A作,如图所示:
∵,,
∴,
∵,
∴,
∴,
故选:A.
9.D
解:
,
.
故选D.
10.A
解:在直角△ADE中,∠DAE=α,AE=5米,
∴,
∴DE=5tanα.
又CE=AB=1.7米,
∴CD=CE+DE=(1.7+5tanα)米.
故选:A.
11.D
解:在中,,
(米,
在中,,
(米,
米,
故选:D.
12.D
解:作DF⊥AB于点F,
∵斜坡DE的坡比为1:2,CE=72米,
∴,
∴CD=36米,
∵DC⊥BC,FB⊥BC,DF⊥AB,
∴四边形BCDF是矩形,
∴DC=BF=36米,BC=DF,
∵∠ADF=37°,∠ACB=48°,tan∠ADF,tan∠ACB,
tan37°,tan48°,
∴,,
解得AF≈77,
∴AB=AF+BF=77+36=113(米),
故选:D.
13.10
解:如图,
∵BC⊥AE,
∴∠AEB=90°,
∵∠EAB=30°,AB=10千米,
∴BE=5米,AE=5千米,
∴CE=BC-BE=20-5=15(千米),
∴AC= (千米),
故答案为:10.
14.
解:直角三角形中,米,
直角三角形中,米,
因此,米,
故答案是:.
15.
解:由题意可得,
∠CAO=∠DBO=60°,∠COA=∠DOB=90°,
∵tan∠CAO=,tan∠DBO=,
∴tan60°=,tan60°=,
∴OC=OA,(OA+3)=OC+CD,
∴(OA+3)=OA+CD,
解得CD=3,
故答案为:3.
16..
解:过P作PC⊥AB于C,
∵新疆部A位于学校主教学楼P南偏东45°方向,
∴∠A=45°
∴∠CPA=90°-∠A=45°,
∴PC=AC,
设AC=PC=x,
∵PA=60米
∴AC=PC=PAcos45°=60,
∵综合楼B处在教学楼北偏东30°方向,
∴∠B=30°,
∴PB=2PC=,
在Rt△BCP中,BC=PBcos30°,
∴AB=BC+AC米.
故答案为:.
17.
解:如图,过点B作BH⊥AC于点H,
设 米,
∵,∠BHC=90°,
∴ ,
∵,
∴∠ABH=45°,
∴∠ABH=∠BAC,
∴AH=BH=x,
∵米,
∴ ,解得: ,
∴AH=BH=12
∴ (米).
故答案为: .
18.A、B两点间的距离约为(4+4)千米.
解:过点C作CD⊥AB于点D,如图所示.
在Rt△ACD中,AC=8(千米),∠CAD=30°,∠CDA=90°,
∴CD=AC sin∠CAD=4(千米),AD=AC cos∠CAD=4(千米).
在Rt△BCD中,CD=4(千米),∠BDC=90°,∠CBD=45°,
∴∠BCD=45°,
∴BD=CD=4(千米),
∴AB=AD+BD=4+4(千米).
答:A、B两点间的距离约为(4+4)千米.
19.0.286
解:由题意得:m,m,
所以山坡的坡度约为
20.
解:如图所示:过点C作CD⊥AB于点D,
∵一艘货轮以36km/h的速度在海面上航行,向北航行40min后到达C点,
∴AC=36×40÷60=24(km),
∵∠A=45°,∠BCN=75°,
∴∠ACD=45°,∠DCB=60°,∠B=30°,
则DC=ACsin45°=12 (km),
故BC=2CD=24≈33.94(km).
答:此时货轮与灯塔B的距离约为33.94km.
21.
解:过点A作AE⊥BC于点E,
在直角△ABE中,tan∠ABE= ,
∴BE= = ≈49.0mm,
∴BC=AD+2BE=180+2×49.0=278mm.
答:里口宽BC是278mm.
22.(1)BE的长为36cm;(2)变形前后两轴心BC的长度增加了4cm.
解:(1)如图1,过点D作DF⊥BE于点F,
由题意知BD=DE=30cm,
∴BF=BDcos∠ABC=30×=18(cm),
∴BE=2BF=36(cm);
答:BE的长为36cm;
(2)如图2,过点D作DM⊥BC于M,过点E作EN⊥BC于点N,
由题意知四边形DENM是矩形,
∴MN=DE=30cm,
在Rt△DBM中,BM=BDcos∠ABC=30×=18(cm),
EN=DM=BDsin∠ABC=30×=24(cm),
在Rt△CEN中,CE=40cm,
∴由勾股定理可得CN==32(cm),
则BC=18+30+32=80(cm),
原来BC=36+40=76(cm),
80-76=4(cm),
∴变形前后两轴心BC的长度增加了4cm.
.
一、单选题
1.河堤横断面如图所示,堤高米,迎水坡的坡比为,则AB的长为( )
A.米 B.米 C.18米 D.21米
2.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i =1:0.75,坡长BC=25米,则此时AB 的长约为( )(参考数据:sin40°≈ 0.64,cos40° ≈ 0.77,tan40°≈ 0.84)
A.10.4 米 B.12.4 米 C.27.4 米 D.22.4 米
3.知识改变世界,科技改变生活,导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C地表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地,导航显示车辆应沿北偏东方向行驶至B地,再沿北偏西方向行驶一段距离才能到达C地,则B,C两地的距离为( ).(结果保留根号,参考数据:,,)
A. B. C. D.
4.重庆朝天门码头位于重庆市渝中半岛的嘉陵江与长江交汇处,是重庆最古老的码头.如图,小王在码头某点E处测得朝天门广场上的某高楼AB的顶端A的仰角为45°,接着他沿着坡度为1:2.4的斜坡EC走了26米到达坡顶C处,到C处后继续朝高楼AB的方向前行18米到D处,在D处测得A的仰角为74°,则此时小王距高楼的距离BD为( )米.(结果精确到1米,参考数据:sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
A.12 B.13 C.15 D.16
5.如图,为了测量某建筑物BC的高度,某数学兴趣小组采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,先沿斜坡AD行走390米至坡顶D处,再从D处沿水平方向继续前行一定距离后至点E处,在E点处测得该建筑物顶端C的仰角为68°,建筑物底端B的俯角为57°,其中A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4,根据数学兴趣小组的测量数据,计算得出建筑物BC的高度约为( )(计算结果精确到0.1米,参考数据:sin68°≈0.93,tan68°≈2.48,sin57°≈0.84,tan57°≈1.54)
A.241.6米 B.391.6米 C.422.9米 D.572.9米
6.图1是某公园的一个滑梯,图2是其示意图.滑梯的高BC为2m,坡角∠A为60°,由于滑梯坡角过大存在安全隐忠,公园管理局决定对滑梯进行整改,要在高度不变的前提下,通过加长滑梯的水平距离AB,使得坡角∠A满足30°≤∠A≤45°,则AB加长的距离可以是( )
(参考数据:≈1.414,≈1.732)
A.0.8m B.1.6m C.2.4m D.3.2m
7.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.米 B.米 C.米 D.米
8.如图是一架人字梯,已知米,AC与地面BC的夹角为,则两梯脚之间的距离BC为( )
A.米 B.米 C.米 D.米
9.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得.据此,可求得学校与工厂之间的距离等于( )
A. B. C. D.
10.小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为α,则点D到地面的距离CD是( )
A.(1.7+5tanα)米 B.(1.7+)米
C.(1.7+5sinα)米 D.(1.7+)米
11.如图,胡同左右两侧是竖直的墙,一架米长的梯子BC斜靠在右侧墙壁上,测得梯子与地面的夹角为45°,此时梯子顶端B恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达D处,此时测得梯子AD与地面的夹角为60°,则胡同左侧的通道拓宽了( )
A.米 B.3米 C.米 D.米
12.如图,线段AB表示一信号塔,DE表示一斜坡,DC⊥CE.且B、C、E三点在同一水平线上,点A、B、C、D、E在同一平面内,斜坡DE的坡比为1:2,CE=72米.某人站在坡顶D处测得塔顶A点的仰角为37°,站在坡底C处测得塔顶A点的仰角为48°(人的身高忽略不计),则信号塔的高度AB为( )(结果精确到1米)
(参考数据:sin37°,tan37°,sin48°,tan48°)
A.77 B.62 C.109 D.113
二、填空题
13.如图,一艘船从A向北偏东30°的方向行驶10千米到达B处,再从B处向正西方向行驶20千米到达C处,这时这艘船与A的距离为_______千米.
14.如图所示,CD、EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明沿直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,则小明由点A移动到点N的距离是___米.
15.如图,小石同学在A,B两点分别测得某建筑物上条幅两端C,D两点的仰角均为60°,若点O,A,B在同一直线上,A,B两点间距离为3米,则条幅的高CD为______米.
16.如图,新疆部A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,某同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时这位同学一共走的距离为______米.
17.一颗珍贵的百年老树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,做法如下:在地面上选取一点,测得,米,,则这棵树的高约为________米.(结果精确到0.1,参考数据:,,)
三、解答题
18.如图,三条笔直公路两两相交,交点分别为A,B,C,测得∠CAB=30°,∠ABC=45°,AC=8千米,求A,B两点间的距离.(结果保留根号)
19.如图,某人从山脚下的点A走了后到达山顶的点B,已知点B到山脚的垂直距离为,求山的坡度(,结果精确到0.001).
20.如图,一艘货轮以的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B.货轮继续向北航行后到达C处,发现灯塔B在它北偏东方向,求此时货轮与灯塔B的距离(结果精确到).
21.如图,燕尾槽的横截面是梯形,其中,燕尾角,外口宽,燕尾槽深度是,求它的里口宽(结果精确到; sin55°=0.82,cos55°=0.57,tan55°=1.43).
22.如图1是某工厂生产的某种多功能儿童车,根据需要可变形为滑板车或三轮车,图2,图3是其示意图,已知前后车轮半径相同,车杆AB的长为60cm,点D是AB的中点,前支撑板DE=30cm,后支撑板EC=40cm,车杆AB与BC所成的∠ABC=53°.(参考数据:)
(1)如图2,当支撑点E在水平线BC上时,求支撑点E与前轮轴心B之间的距离BE的长;
(2)如图3,当座板DE与地平面保持平行时,问变形前后两轴心BC的长度有没有发生变化?若不变,请通过计算说明;若变化,请求出变化量.
参考答案
1.C
解:∵BC=9米,迎水坡AB的坡比为1:,
∴,
解得,AC=9,
∴AB==18,
故选:C.
2.A
解:如图,延长交延长线于点,作于点,
,
,
四边形为矩形,
,,
,
设、,
由可得,,
解得:或(舍去),
则,,
,
在中,,
,
故选:A.
3.C
解:如图所示,作BD⊥AC于D点,则∠ADB=∠CDB=90°,
则由题意可知,∠A=60°,∠ABD=30°,∠CBD=53°,
在Rt△ABD中,设,则,
∴,
在Rt△CBD中,,
即:,
解得:,
经检验,是上述分式方程的解,
∴,
∵,
∴,
即:,
故选:C.
4.B
解:过E作EH⊥AB交AB的延长线于H,
过C作CG⊥EH于G,
则CG=BH,BC=GH,
∵CE=26,=1:2.4,
∴CG=10,EG=24,
∴BH=CG=10,
设BD=x,
在Rt△ABD中,
∵∠ADB=74°,
∴AB=tan74° x≈3.49x,
∴AH=AB+BH=3.49x+10,
∵EH=EG+GH=24+18+x,
∵∠AEH=45°,
∴AH=EH,
∴3.49x+10=24+18+x,
解得:x≈13,
∴BD=13(米),
答:小王距高楼的距离BD为13米.
故选:B.
5.B
解:如图作DH⊥AB于H,延长DE交BC于F.
在Rt△ADH中,AD=390米,DH:AH=1:2.4,
∴DH=150(米),
∵四边形DHBF是矩形,
∴BF=DH=150米,
在Rt△EFB中,tan57°=,
∴EF=,
在Rt△EFC中,FC=EF tan68°,
∴CF≈×2.48≈241.6(米),
∴BC=BF+CF=391.6米.
故选:B.
6.B
解:如图,在Rt△ABC,∠CAB=60°,BC=2,
∴AB===,
当坡角为45°时,有BD=BC=2,
∴DA=2﹣AB=2﹣≈0.85(m),
当坡角为30°时,有BE==(m),
∴EA=BE﹣AB=2﹣≈2.31(m),
当坡角满足30°≤∠A≤45°,
∴AB加长的距离x的取值范围为0.85≤x≤2.31,
故选:B.
7.A
解:在Rt△ABC中,
,
即,
故选:A.
8.A
解:过点A作,如图所示:
∵,,
∴,
∵,
∴,
∴,
故选:A.
9.D
解:
,
.
故选D.
10.A
解:在直角△ADE中,∠DAE=α,AE=5米,
∴,
∴DE=5tanα.
又CE=AB=1.7米,
∴CD=CE+DE=(1.7+5tanα)米.
故选:A.
11.D
解:在中,,
(米,
在中,,
(米,
米,
故选:D.
12.D
解:作DF⊥AB于点F,
∵斜坡DE的坡比为1:2,CE=72米,
∴,
∴CD=36米,
∵DC⊥BC,FB⊥BC,DF⊥AB,
∴四边形BCDF是矩形,
∴DC=BF=36米,BC=DF,
∵∠ADF=37°,∠ACB=48°,tan∠ADF,tan∠ACB,
tan37°,tan48°,
∴,,
解得AF≈77,
∴AB=AF+BF=77+36=113(米),
故选:D.
13.10
解:如图,
∵BC⊥AE,
∴∠AEB=90°,
∵∠EAB=30°,AB=10千米,
∴BE=5米,AE=5千米,
∴CE=BC-BE=20-5=15(千米),
∴AC= (千米),
故答案为:10.
14.
解:直角三角形中,米,
直角三角形中,米,
因此,米,
故答案是:.
15.
解:由题意可得,
∠CAO=∠DBO=60°,∠COA=∠DOB=90°,
∵tan∠CAO=,tan∠DBO=,
∴tan60°=,tan60°=,
∴OC=OA,(OA+3)=OC+CD,
∴(OA+3)=OA+CD,
解得CD=3,
故答案为:3.
16..
解:过P作PC⊥AB于C,
∵新疆部A位于学校主教学楼P南偏东45°方向,
∴∠A=45°
∴∠CPA=90°-∠A=45°,
∴PC=AC,
设AC=PC=x,
∵PA=60米
∴AC=PC=PAcos45°=60,
∵综合楼B处在教学楼北偏东30°方向,
∴∠B=30°,
∴PB=2PC=,
在Rt△BCP中,BC=PBcos30°,
∴AB=BC+AC米.
故答案为:.
17.
解:如图,过点B作BH⊥AC于点H,
设 米,
∵,∠BHC=90°,
∴ ,
∵,
∴∠ABH=45°,
∴∠ABH=∠BAC,
∴AH=BH=x,
∵米,
∴ ,解得: ,
∴AH=BH=12
∴ (米).
故答案为: .
18.A、B两点间的距离约为(4+4)千米.
解:过点C作CD⊥AB于点D,如图所示.
在Rt△ACD中,AC=8(千米),∠CAD=30°,∠CDA=90°,
∴CD=AC sin∠CAD=4(千米),AD=AC cos∠CAD=4(千米).
在Rt△BCD中,CD=4(千米),∠BDC=90°,∠CBD=45°,
∴∠BCD=45°,
∴BD=CD=4(千米),
∴AB=AD+BD=4+4(千米).
答:A、B两点间的距离约为(4+4)千米.
19.0.286
解:由题意得:m,m,
所以山坡的坡度约为
20.
解:如图所示:过点C作CD⊥AB于点D,
∵一艘货轮以36km/h的速度在海面上航行,向北航行40min后到达C点,
∴AC=36×40÷60=24(km),
∵∠A=45°,∠BCN=75°,
∴∠ACD=45°,∠DCB=60°,∠B=30°,
则DC=ACsin45°=12 (km),
故BC=2CD=24≈33.94(km).
答:此时货轮与灯塔B的距离约为33.94km.
21.
解:过点A作AE⊥BC于点E,
在直角△ABE中,tan∠ABE= ,
∴BE= = ≈49.0mm,
∴BC=AD+2BE=180+2×49.0=278mm.
答:里口宽BC是278mm.
22.(1)BE的长为36cm;(2)变形前后两轴心BC的长度增加了4cm.
解:(1)如图1,过点D作DF⊥BE于点F,
由题意知BD=DE=30cm,
∴BF=BDcos∠ABC=30×=18(cm),
∴BE=2BF=36(cm);
答:BE的长为36cm;
(2)如图2,过点D作DM⊥BC于M,过点E作EN⊥BC于点N,
由题意知四边形DENM是矩形,
∴MN=DE=30cm,
在Rt△DBM中,BM=BDcos∠ABC=30×=18(cm),
EN=DM=BDsin∠ABC=30×=24(cm),
在Rt△CEN中,CE=40cm,
∴由勾股定理可得CN==32(cm),
则BC=18+30+32=80(cm),
原来BC=36+40=76(cm),
80-76=4(cm),
∴变形前后两轴心BC的长度增加了4cm.
.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
