2021年上海市浦东新区高二期中考试数学试卷(2021.11)(图片版 含答案)
文档属性
| 名称 | 2021年上海市浦东新区高二期中考试数学试卷(2021.11)(图片版 含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 09:41:32 | ||
图片预览

文档简介
021学年度第一学期期中考试高二数学试卷
2021年11月2日考试时间:90分钟满分:100分
请将答案填写在答题卡上
、填空题(本题共有12个小题,每小题3分,满分36分
1.公理2:不在同一直线上的
点确定一个平面
2.直线与平面垂直的判定定理:如果一条直线与一个平面上的
直线都垂直
那么此直线与该平面垂直
3.三垂线定理:平面上的一条直线和这个平面的一条斜线垂直的充要条件是它和这条斜线
在
4.一个球的半径为3,则它的体积是
5.一个圆柱的底面半径为3cm,高为4cm,则它的侧面积为
6.已知斜线段的长度是斜线段在这个平面内射影的长的两倍,则这条斜线和这个平面所成
的角的大小为
个正四棱柱底面边长为1,高为2,则它的表面积是
图是一个正方体的平面展开图,在这个正方体中,下列说法中,正确的序号是
1)直线AF与直线DE相交
(2)直线CH与直线DE平行
(3)直线BG与直线DE是异面直线
(4)直线CH与直线BG成60°角
9.若空间三条直线a⊥c,b⊥c,则a,b的位置关系是
10.在正方体ABCD-A1BC1D1中,平面ABCD与平面ABCD所成的锐二面角的大小
11.在长方体的12条棱之中,我们把两条异面的棱称为“一对”,则12条棱中,共有
对异血直线
12.半面内两直线有三种位置关系:相交,平行与重合,已知两个相交平面a,B与两直线
在a内的射影为S1,s2,在内的射影为42·试写
足的条件,使之一定能成为1,l2是异面直线的充分条件是
单项选择题(本题共有4个小题,每小题3分,满分12分)
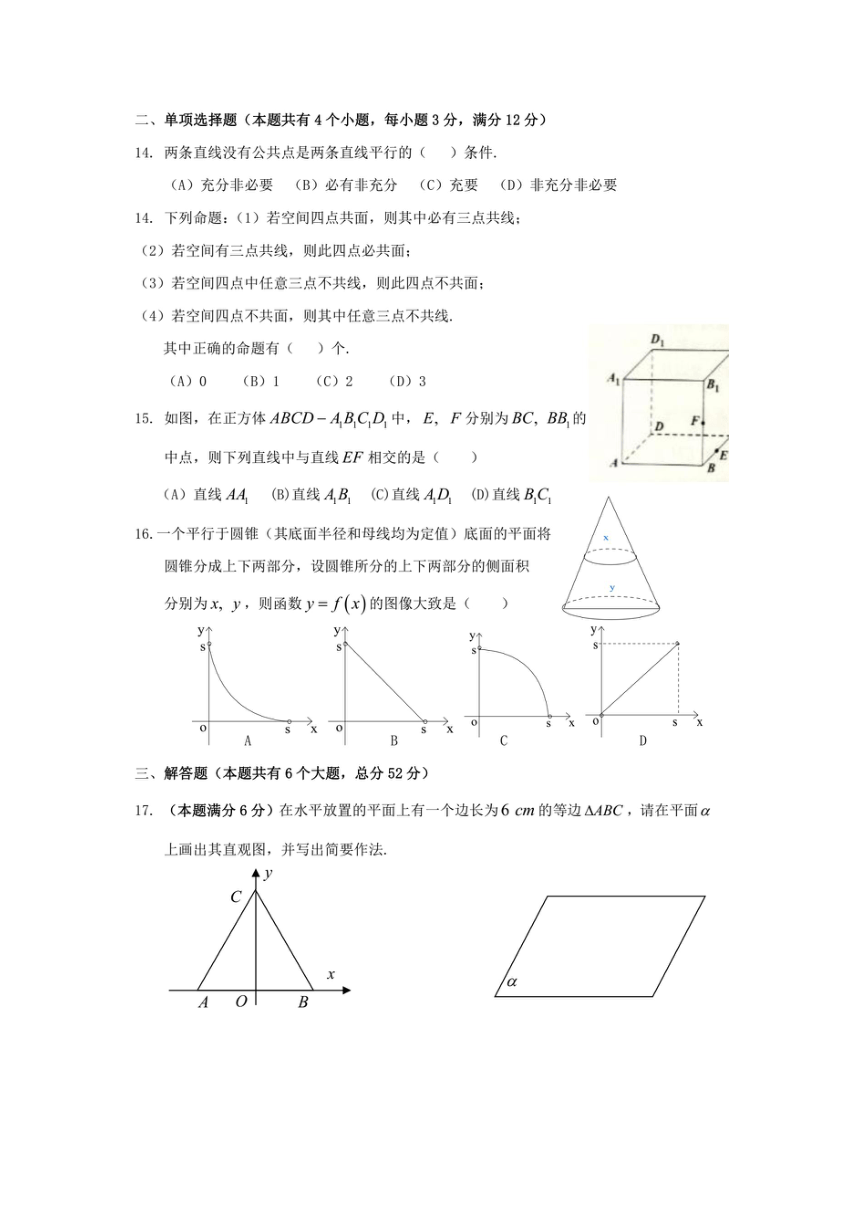
14.两条直线没有公共点是两条直线平行的
(A)充分非必要(B)必有非充分(C)充要(D)非充分非必要
14.下列命题:(1)若空间四点共面,则其中必有三点共线
(2)若空间有三点共线,则此四点必共面
(3)若空间四点中任意三点不共线,则此四点不共面
(4)若空间四点不共面,则其中任意三点不共线
其中正确的命题有()个
D
15.如图,在正方体ABCD-ABC1D1中,E,F分别为BC,BB3的
D F
屮点,则下列直线屮与直线EF相交的是(
(A)直线AA(B)直线AB1(C)直线AD(D)直线BC1
16.一个平行于圆锥(其底面半径和母线均为定值)底面的平面将
圆锥分成上下两部分,设圆锥所分的上下两部分的侧面积
分别为x,y,则函数y=f(x)的图像大致是
解答题(本题共有6个大题,总分52分)
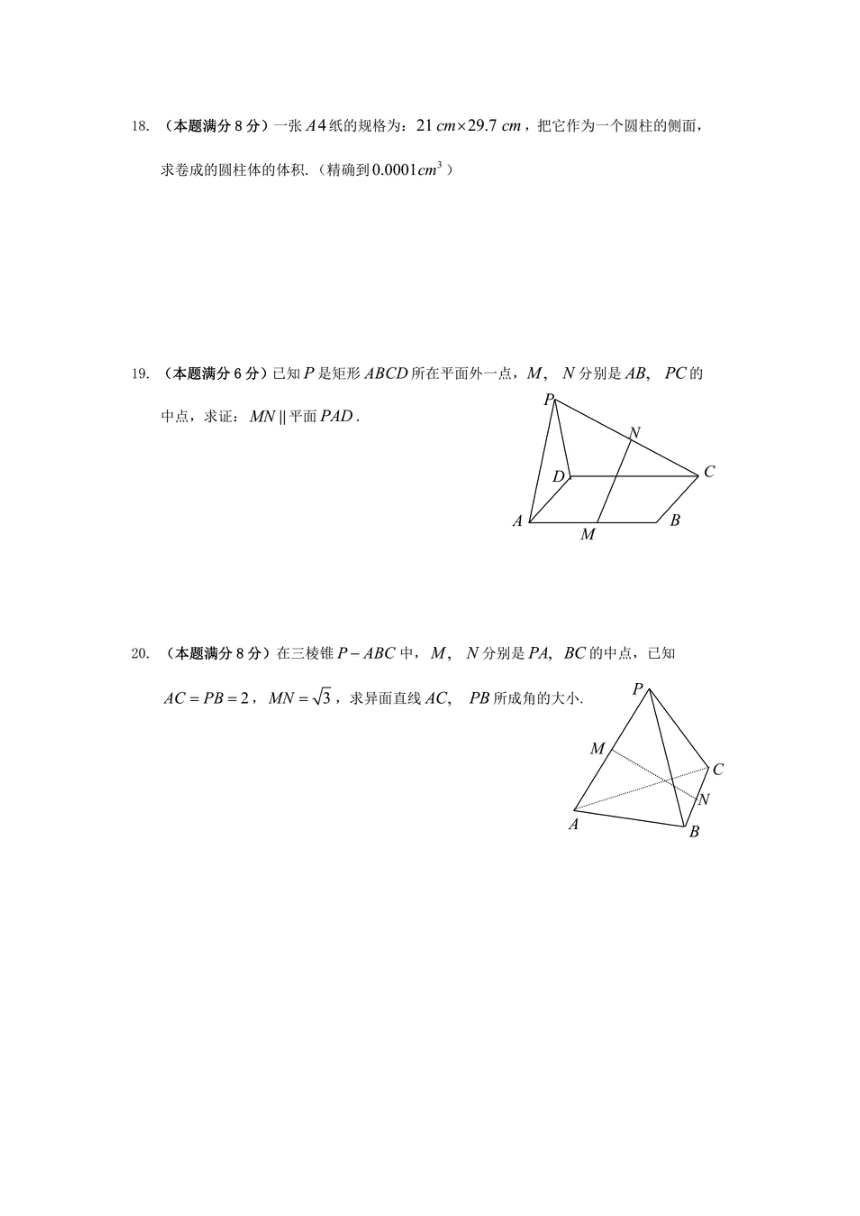
17.(本题满分6分)在水平放置的平面上有一个边长为6cm的等边△ABC,请在平面a
上画出其直观图,并写出简要作法
2021年11月2日考试时间:90分钟满分:100分
请将答案填写在答题卡上
、填空题(本题共有12个小题,每小题3分,满分36分
1.公理2:不在同一直线上的
点确定一个平面
2.直线与平面垂直的判定定理:如果一条直线与一个平面上的
直线都垂直
那么此直线与该平面垂直
3.三垂线定理:平面上的一条直线和这个平面的一条斜线垂直的充要条件是它和这条斜线
在
4.一个球的半径为3,则它的体积是
5.一个圆柱的底面半径为3cm,高为4cm,则它的侧面积为
6.已知斜线段的长度是斜线段在这个平面内射影的长的两倍,则这条斜线和这个平面所成
的角的大小为
个正四棱柱底面边长为1,高为2,则它的表面积是
图是一个正方体的平面展开图,在这个正方体中,下列说法中,正确的序号是
1)直线AF与直线DE相交
(2)直线CH与直线DE平行
(3)直线BG与直线DE是异面直线
(4)直线CH与直线BG成60°角
9.若空间三条直线a⊥c,b⊥c,则a,b的位置关系是
10.在正方体ABCD-A1BC1D1中,平面ABCD与平面ABCD所成的锐二面角的大小
11.在长方体的12条棱之中,我们把两条异面的棱称为“一对”,则12条棱中,共有
对异血直线
12.半面内两直线有三种位置关系:相交,平行与重合,已知两个相交平面a,B与两直线
在a内的射影为S1,s2,在内的射影为42·试写
足的条件,使之一定能成为1,l2是异面直线的充分条件是
单项选择题(本题共有4个小题,每小题3分,满分12分)
14.两条直线没有公共点是两条直线平行的
(A)充分非必要(B)必有非充分(C)充要(D)非充分非必要
14.下列命题:(1)若空间四点共面,则其中必有三点共线
(2)若空间有三点共线,则此四点必共面
(3)若空间四点中任意三点不共线,则此四点不共面
(4)若空间四点不共面,则其中任意三点不共线
其中正确的命题有()个
D
15.如图,在正方体ABCD-ABC1D1中,E,F分别为BC,BB3的
D F
屮点,则下列直线屮与直线EF相交的是(
(A)直线AA(B)直线AB1(C)直线AD(D)直线BC1
16.一个平行于圆锥(其底面半径和母线均为定值)底面的平面将
圆锥分成上下两部分,设圆锥所分的上下两部分的侧面积
分别为x,y,则函数y=f(x)的图像大致是
解答题(本题共有6个大题,总分52分)
17.(本题满分6分)在水平放置的平面上有一个边长为6cm的等边△ABC,请在平面a
上画出其直观图,并写出简要作法
同课章节目录
