人教版九年级数学上册第二十三章 旋转 单元重点知识练习(word解析版)
文档属性
| 名称 | 人教版九年级数学上册第二十三章 旋转 单元重点知识练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 534.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 13:06:15 | ||
图片预览

文档简介
第二十三章 旋转
一、单选题
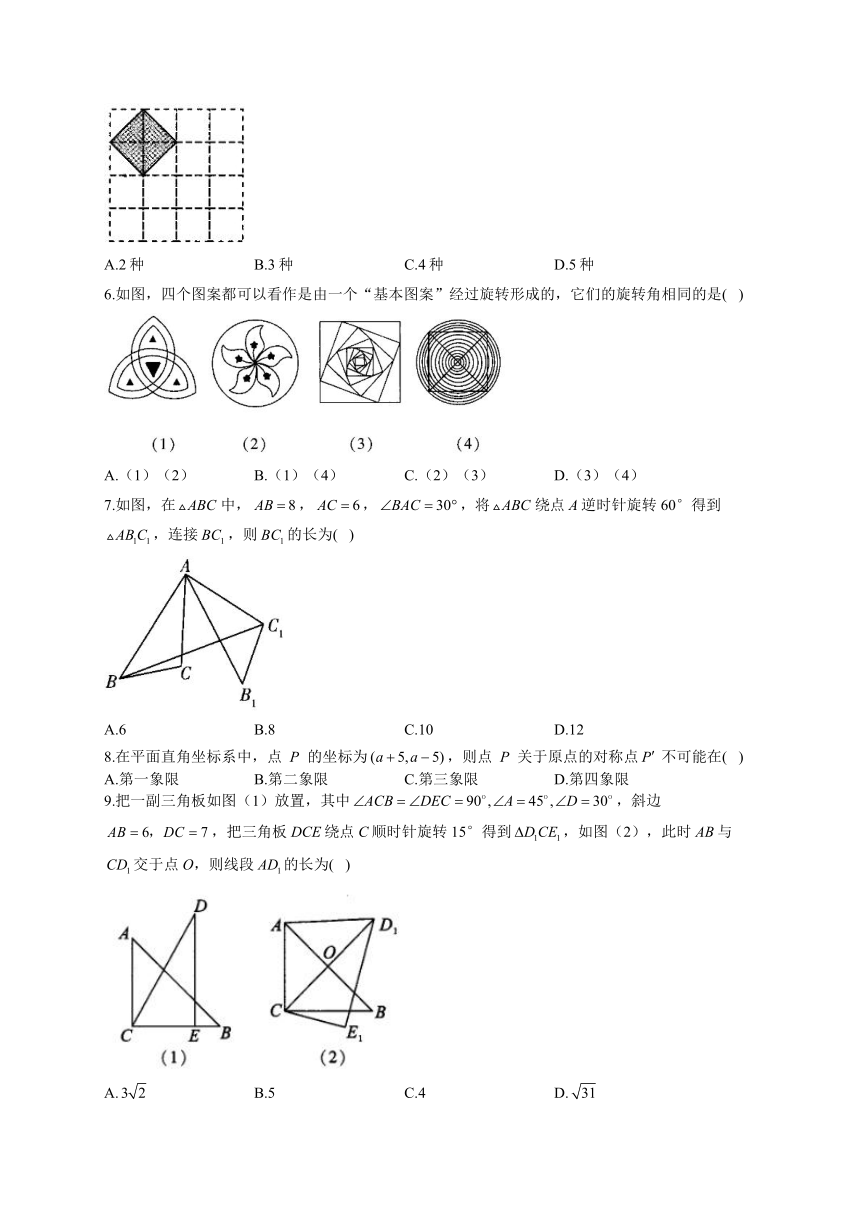
1.“瓦当”是中国古建筑装饰檐头的附件,是中国特有的文化艺术遗产,下列“瓦当”图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.如图,将沿逆时针方向旋转到的位置.下列说法中不正确的是( )
A.点A是旋转中心 B.
C.是一个旋转角 D.
3.把各点的横、纵坐标都乘以-1后,得到的图形是( )
A. B. C. D.
4.如图,将绕点B逆时针旋转,得到,若点A恰好在ED的延长线上,则的度数为( )
A. B. C. D.
5.如图,在的正方形网格中,每个小正方形的顶点为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种 C.4种 D.5种
6.如图,四个图案都可以看作是由一个“基本图案”经过旋转形成的,它们的旋转角相同的是( )
A.(1)(2) B.(1)(4) C.(2)(3) D.(3)(4)
7.如图,在中,,,,将绕点A逆时针旋转60°得到,连接,则的长为( )
A.6 B.8 C.10 D.12
8.在平面直角坐标系中,点的坐标为,则点关于原点的对称点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.把一副三角板如图(1)放置,其中,斜边,把三角板DCE绕点C顺时针旋转15°得到,如图(2),此时AB与交于点O,则线段的长为( )
A. B.5 C.4 D.
二、填空题
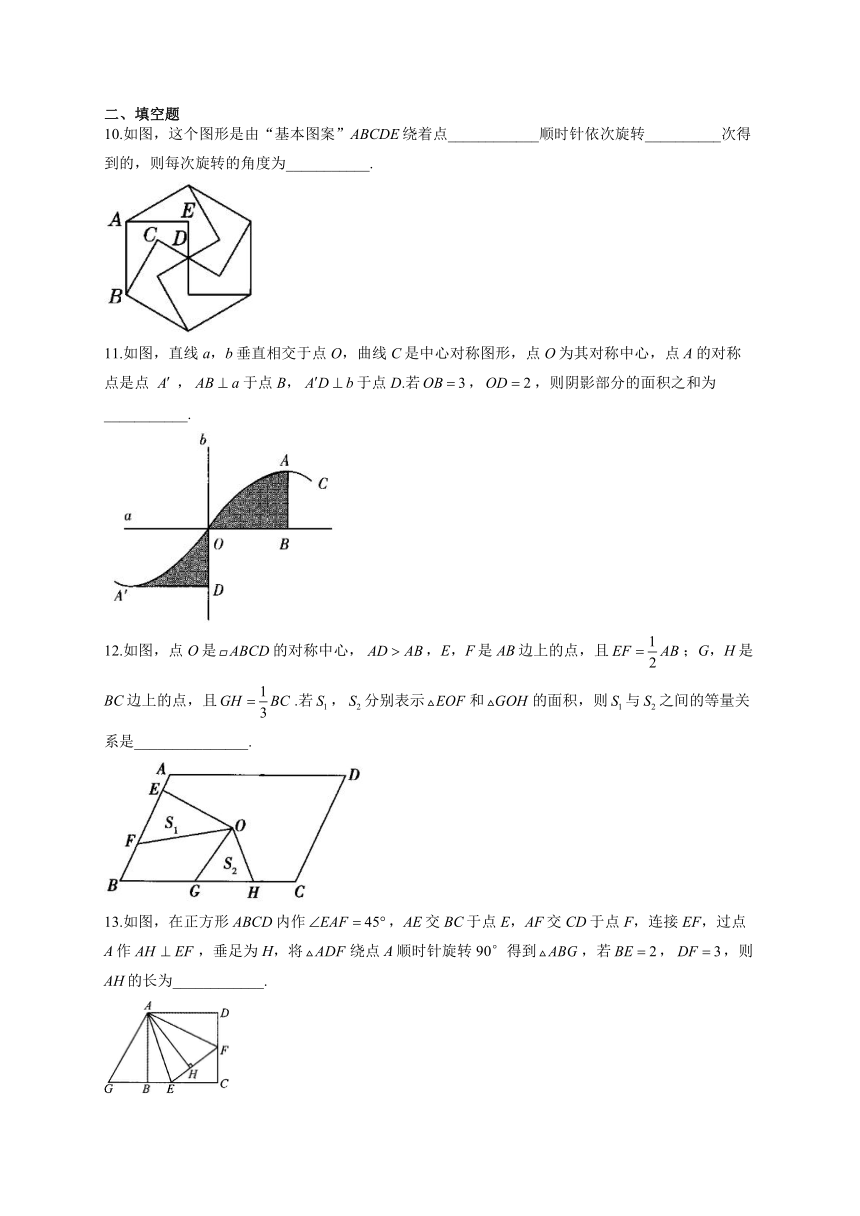
10.如图,这个图形是由“基本图案”ABCDE绕着点____________顺时针依次旋转__________次得到的,则每次旋转的角度为___________.
11.如图,直线a,b垂直相交于点O,曲线C是中心对称图形,点O为其对称中心,点A的对称点是点,于点B,于点D.若,,则阴影部分的面积之和为___________.
12.如图,点O是的对称中心,,E,F是AB边上的点,且;G,H是BC边上的点,且.若,分别表示和的面积,则与之间的等量关系是_______________.
13.如图,在正方形ABCD内作,AE交BC于点E,AF交CD于点F,连接EF,过点A作,垂足为H,将绕点A顺时针旋转90°得到,若,,则AH的长为____________.
三、解答题
14.如图,在的方格纸中,的三个顶点都在格点上.
(1)在图①中,画出一个与成中心对称的格点三角形;
(2)在图②中,画出一个与成轴对称且与有公共边的格点三角形;
(3)在图③中,画出绕着点C按顺时针方向旋转90°后的三角形.
15.如图,在中,,将绕点A旋转至,点E落在边BC上,EF与AC交于点G,求的度数.
参考答案
1.答案:D
解析:选项A既不是轴对称图形,也不是中心对称图形;选项B不是轴对称图形,是中心对称图形;选项C是轴对称图形,不是中心对称图形;选项D既是轴对称图形,又是中心对称图形.故选D.
2.答案:C
解析:将沿逆时针方向旋转到的位置,点A是旋转中心,,,与是旋转角.故A,B,D选项说法正确,C选项说法错误.故选C.
3.答案:C
解析:把各点的横、纵坐标都乘以-1,得到的点与各点关于原点对称,所以得到的图形与关于原点中心对称,故C项符合要求.故选C.
4.答案:C
解析:由题意可得,,,,,,,.故选C.
5.答案:C
解析:如图所示,若使组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.
6.答案:D
解析:(1)中的旋转角为;(2)中的旋转角为;(3)中的旋转角为;(4)中的旋转角为.所以(3)(4)中的旋转角相同.故选D.
7.答案:C
解析:由旋转可得,,.在中,,,.故选C.
8.答案:D
解析:点的坐标为,点关于原点的对称点的坐标为.当时,,此时点在第一象限;当时,,此时的符号可能正也可能负,点在第二象限或第三象限,故点不可能在第四象限.故选D.
9.答案:B
解析:.由题意,得旋转角为15°,又是等腰直角三角形,.故选D.
10.答案:D,5,60°
解析:根据旋转的性质,可知在点D处有6个角,故,所以它的旋转角为60°,即这个图形是由“基本图案”ABCDE绕着点D顺时针依次旋转5次得到的,每次旋转的角度为60°.
11.答案:6
解析:过点A作于点E,曲线C是中心对称图形,点A的对称点是点,,,阴影部分的面积之和等于四边形ABOE的面积,,,,阴影部分的面积之和为.
12.答案:(答案不唯一,填或也可)
解析:设平行四边形ABCD的AB边上的高为,BC边上的高为.点O为平行四边形ABCD的对称中心,,.,,.
13.答案:6
解析:由旋转的性质可知,,,.四边形ABCD为正方形,,又,...在和中,,..,,.设正方形的边长为x,则,.在中,由勾股定理得,,即.解得(舍去).,.
14.答案:(1)如图①所示,为所求作.
(2)如图②所示,为所求作;
(3)如图③所示,为所求作.
15.答案:由旋转的性质可知,,
.
在中,,
,
在中,,
,
.
在中,,
,
.
一、单选题
1.“瓦当”是中国古建筑装饰檐头的附件,是中国特有的文化艺术遗产,下列“瓦当”图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.如图,将沿逆时针方向旋转到的位置.下列说法中不正确的是( )
A.点A是旋转中心 B.
C.是一个旋转角 D.
3.把各点的横、纵坐标都乘以-1后,得到的图形是( )
A. B. C. D.
4.如图,将绕点B逆时针旋转,得到,若点A恰好在ED的延长线上,则的度数为( )
A. B. C. D.
5.如图,在的正方形网格中,每个小正方形的顶点为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种 C.4种 D.5种
6.如图,四个图案都可以看作是由一个“基本图案”经过旋转形成的,它们的旋转角相同的是( )
A.(1)(2) B.(1)(4) C.(2)(3) D.(3)(4)
7.如图,在中,,,,将绕点A逆时针旋转60°得到,连接,则的长为( )
A.6 B.8 C.10 D.12
8.在平面直角坐标系中,点的坐标为,则点关于原点的对称点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.把一副三角板如图(1)放置,其中,斜边,把三角板DCE绕点C顺时针旋转15°得到,如图(2),此时AB与交于点O,则线段的长为( )
A. B.5 C.4 D.
二、填空题
10.如图,这个图形是由“基本图案”ABCDE绕着点____________顺时针依次旋转__________次得到的,则每次旋转的角度为___________.
11.如图,直线a,b垂直相交于点O,曲线C是中心对称图形,点O为其对称中心,点A的对称点是点,于点B,于点D.若,,则阴影部分的面积之和为___________.
12.如图,点O是的对称中心,,E,F是AB边上的点,且;G,H是BC边上的点,且.若,分别表示和的面积,则与之间的等量关系是_______________.
13.如图,在正方形ABCD内作,AE交BC于点E,AF交CD于点F,连接EF,过点A作,垂足为H,将绕点A顺时针旋转90°得到,若,,则AH的长为____________.
三、解答题
14.如图,在的方格纸中,的三个顶点都在格点上.
(1)在图①中,画出一个与成中心对称的格点三角形;
(2)在图②中,画出一个与成轴对称且与有公共边的格点三角形;
(3)在图③中,画出绕着点C按顺时针方向旋转90°后的三角形.
15.如图,在中,,将绕点A旋转至,点E落在边BC上,EF与AC交于点G,求的度数.
参考答案
1.答案:D
解析:选项A既不是轴对称图形,也不是中心对称图形;选项B不是轴对称图形,是中心对称图形;选项C是轴对称图形,不是中心对称图形;选项D既是轴对称图形,又是中心对称图形.故选D.
2.答案:C
解析:将沿逆时针方向旋转到的位置,点A是旋转中心,,,与是旋转角.故A,B,D选项说法正确,C选项说法错误.故选C.
3.答案:C
解析:把各点的横、纵坐标都乘以-1,得到的点与各点关于原点对称,所以得到的图形与关于原点中心对称,故C项符合要求.故选C.
4.答案:C
解析:由题意可得,,,,,,,.故选C.
5.答案:C
解析:如图所示,若使组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.
6.答案:D
解析:(1)中的旋转角为;(2)中的旋转角为;(3)中的旋转角为;(4)中的旋转角为.所以(3)(4)中的旋转角相同.故选D.
7.答案:C
解析:由旋转可得,,.在中,,,.故选C.
8.答案:D
解析:点的坐标为,点关于原点的对称点的坐标为.当时,,此时点在第一象限;当时,,此时的符号可能正也可能负,点在第二象限或第三象限,故点不可能在第四象限.故选D.
9.答案:B
解析:.由题意,得旋转角为15°,又是等腰直角三角形,.故选D.
10.答案:D,5,60°
解析:根据旋转的性质,可知在点D处有6个角,故,所以它的旋转角为60°,即这个图形是由“基本图案”ABCDE绕着点D顺时针依次旋转5次得到的,每次旋转的角度为60°.
11.答案:6
解析:过点A作于点E,曲线C是中心对称图形,点A的对称点是点,,,阴影部分的面积之和等于四边形ABOE的面积,,,,阴影部分的面积之和为.
12.答案:(答案不唯一,填或也可)
解析:设平行四边形ABCD的AB边上的高为,BC边上的高为.点O为平行四边形ABCD的对称中心,,.,,.
13.答案:6
解析:由旋转的性质可知,,,.四边形ABCD为正方形,,又,...在和中,,..,,.设正方形的边长为x,则,.在中,由勾股定理得,,即.解得(舍去).,.
14.答案:(1)如图①所示,为所求作.
(2)如图②所示,为所求作;
(3)如图③所示,为所求作.
15.答案:由旋转的性质可知,,
.
在中,,
,
在中,,
,
.
在中,,
,
.
同课章节目录
