5.2 平行四边形的判定 课件(共22张PPT)
文档属性
| 名称 | 5.2 平行四边形的判定 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 08:28:47 | ||
图片预览







文档简介
(共22张PPT)
第五章 平行四边形
2 平行四边形的判定
知识点一 平行四边形的判定定理(一)
内容 几何语言 图形
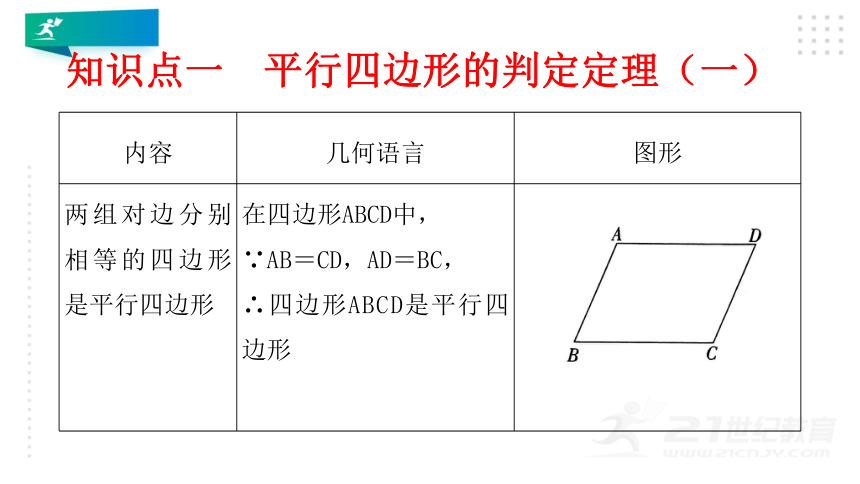
两组对边分别相等的四边形是平行四边形 在四边形ABCD中, ∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形
例1 如图所示,四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F,试证明四边形BFDE是平行四边形.
分析 先根据平行四边形的性质得到相等的角和线段,从而证明△ABF与△CDE全等,得到相等的线段,再根据两组对边分别相等的四边形是平行四边形证明.
证明 因为四边形ABCD是平行四边形,所以∠ADC=∠ABC,∠A=∠C,AB=CD,
AD=BC,AB∥CD,因为DE平分∠ADC,BF平分∠ABC,
所以∠CDE=∠ADC,∠ABF= ∠ABC,所以∠CDE=∠ABF.
在△ABF与△CDE中,
所以△ABF≌△CDE(ASA),所以BF=DE,AF=CE.
因为AD=BC,所以AF-AD=CE-BC,即DF=BE,又BF=DE,所以四边形BFDE是平行四边形.
知识点二 平行四边形的判定定理(二)
内容 几何语言 图形
一组对边平行且相等的四边形是平行四边形 在四边形ABCD中,∵AB=CD(或AD=BC),AB∥CD(或AD∥BC),∴四边形ABCD是平行四边形
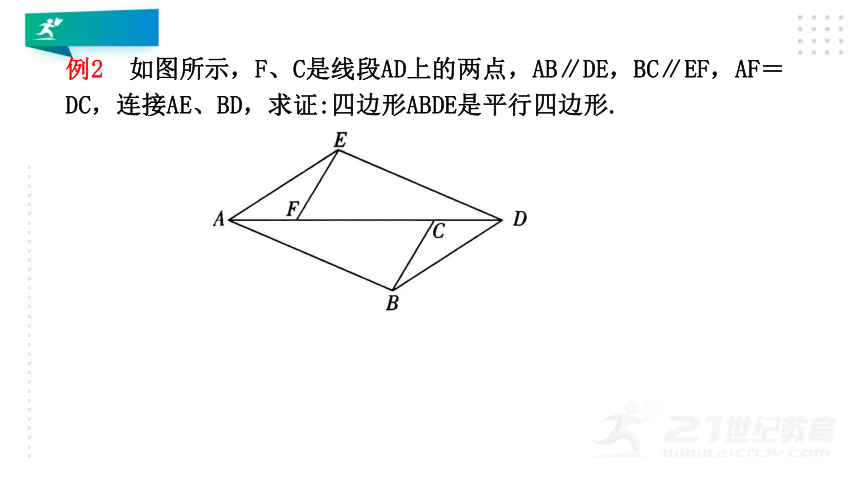
例2 如图所示,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE、BD,求证:四边形ABDE是平行四边形.
分析 要证明四边形ABDE是平行四边形,只要证明AB=DE就可以了,而证明AB=DE可以通过证明△ABC≌△DEF来实现.
分析 要证明四边形ABDE是平行四边形,只要证明AB=DE就可以了,而证明AB=DE可以通过证明△ABC≌△DEF来实现.
证明 ∵AF=DC,∴AF+FC=DC+FC,即AC=DF.
∵AB∥DE,∴∠BAC=∠EDF.
∵BC∥EF,∴∠ACB=∠DFE.
∴△ABC≌△DEF.∴AB=DE.
又∵AB∥DE,∴四边形ABDE是平行四边形.
分析 要证明四边形ABDE是平行四边形,只要证明AB=DE就可以了,而证明AB=DE可以通过证明△ABC≌△DEF来实现.
证明 ∵AF=DC,∴AF+FC=DC+FC,即AC=DF.
∵AB∥DE,∴∠BAC=∠EDF.
∵BC∥EF,∴∠ACB=∠DFE.
∴△ABC≌△DEF.∴AB=DE.
又∵AB∥DE,∴四边形ABDE是平行四边形.
点拨 利用一组对边平行且相等的四边形是平行四边形证明时,一定要注意:是相等的两条边平行,而不是一组对边相等,另一组对边平行,这样的四边形不一定是平行四边形,可能是等腰梯形.
知识点三 平行四边形的判定定理(三)
内容 几何语言 图形
对角线互相平分的四边形是平行四边形 在四边形ABCD中,对角线AC、BD交于点O,∵OA=OC,OB=OD,∴四边形ABCD是平行四边形
例3 如图所示,四边形ABCD中,AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F∠AEF=∠EFC,AD=BC.连接AF、EC.
证明:四边形AFCE是平行四边形.
分析 首先证明四边形ABCD是平行四边形,得到AO=CO,然后证明△OAE≌△OCF(ASA),得到OE=OF,可得出结论.
分析 首先证明四边形ABCD是平行四边形,得到AO=CO,然后证明△OAE≌△OCF(ASA),得到OE=OF,可得出结论.
证明 ∵∠AEF=∠EFC,∴AD∥BC.
∵AD=BC,∴四边形ABCD是平行四边形,∴AO=CO,
又∵AD∥BC,∴∠EAC=∠FCA,
在△OAE和△OCF中, ∴△OAE≌△OCF(ASA).∴OE=OF.
又∵AO=CO,∴四边形AFCE是平行四边形.
点拨 在应用对角线互相平分的四边形是平行四边形证明时,只说明一条对角线被另一条对角线平分就认为四边形是平行四边形是错误的.
经典例题
题型 平行四边形的判定与性质的综合运用
例 如图所示,已知D,E,F分别在△ABC的边BC,AB,AC上,且DE∥AF,DE=AF,将FD延长到点G,使FG=2DF,连接AG,则ED与AG互相平分吗?请说明理由.
分析 由一组对边平行且相等的四边形是平行四边形得四边形AEGD是平行四边形,即可得出结论.
分析 由一组对边平行且相等的四边形是平行四边形得四边形AEGD是平行四边形,即可得出结论.
解析 ED与AG互相平分.
理由:如图所示,连接EG,AD.
∵DE∥AF,DE=AF,∴四边形AEDF是平行四边形.
∴AE∥DF,AE=DF.
又∵FG=2DF,∴DG=DF.∴AE=DG.
又∵AE∥DG,∴四边形AEGD是平行四边形.∴ED与AG互相平分.
方法归纳 平行四边形的性质定理与判定定理是互逆的性质定理是已知平行四边形,从而得到对边相等、对角相等、对角线互相平分等结论;判定定理是由四边形的两组对边分别相等、两组对角分别相等、对角线互相平分等条件来证明这个四边形为平行四边形.
第五章 平行四边形
2 平行四边形的判定
知识点一 平行四边形的判定定理(一)
内容 几何语言 图形
两组对边分别相等的四边形是平行四边形 在四边形ABCD中, ∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形
例1 如图所示,四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F,试证明四边形BFDE是平行四边形.
分析 先根据平行四边形的性质得到相等的角和线段,从而证明△ABF与△CDE全等,得到相等的线段,再根据两组对边分别相等的四边形是平行四边形证明.
证明 因为四边形ABCD是平行四边形,所以∠ADC=∠ABC,∠A=∠C,AB=CD,
AD=BC,AB∥CD,因为DE平分∠ADC,BF平分∠ABC,
所以∠CDE=∠ADC,∠ABF= ∠ABC,所以∠CDE=∠ABF.
在△ABF与△CDE中,
所以△ABF≌△CDE(ASA),所以BF=DE,AF=CE.
因为AD=BC,所以AF-AD=CE-BC,即DF=BE,又BF=DE,所以四边形BFDE是平行四边形.
知识点二 平行四边形的判定定理(二)
内容 几何语言 图形
一组对边平行且相等的四边形是平行四边形 在四边形ABCD中,∵AB=CD(或AD=BC),AB∥CD(或AD∥BC),∴四边形ABCD是平行四边形
例2 如图所示,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE、BD,求证:四边形ABDE是平行四边形.
分析 要证明四边形ABDE是平行四边形,只要证明AB=DE就可以了,而证明AB=DE可以通过证明△ABC≌△DEF来实现.
分析 要证明四边形ABDE是平行四边形,只要证明AB=DE就可以了,而证明AB=DE可以通过证明△ABC≌△DEF来实现.
证明 ∵AF=DC,∴AF+FC=DC+FC,即AC=DF.
∵AB∥DE,∴∠BAC=∠EDF.
∵BC∥EF,∴∠ACB=∠DFE.
∴△ABC≌△DEF.∴AB=DE.
又∵AB∥DE,∴四边形ABDE是平行四边形.
分析 要证明四边形ABDE是平行四边形,只要证明AB=DE就可以了,而证明AB=DE可以通过证明△ABC≌△DEF来实现.
证明 ∵AF=DC,∴AF+FC=DC+FC,即AC=DF.
∵AB∥DE,∴∠BAC=∠EDF.
∵BC∥EF,∴∠ACB=∠DFE.
∴△ABC≌△DEF.∴AB=DE.
又∵AB∥DE,∴四边形ABDE是平行四边形.
点拨 利用一组对边平行且相等的四边形是平行四边形证明时,一定要注意:是相等的两条边平行,而不是一组对边相等,另一组对边平行,这样的四边形不一定是平行四边形,可能是等腰梯形.
知识点三 平行四边形的判定定理(三)
内容 几何语言 图形
对角线互相平分的四边形是平行四边形 在四边形ABCD中,对角线AC、BD交于点O,∵OA=OC,OB=OD,∴四边形ABCD是平行四边形
例3 如图所示,四边形ABCD中,AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F∠AEF=∠EFC,AD=BC.连接AF、EC.
证明:四边形AFCE是平行四边形.
分析 首先证明四边形ABCD是平行四边形,得到AO=CO,然后证明△OAE≌△OCF(ASA),得到OE=OF,可得出结论.
分析 首先证明四边形ABCD是平行四边形,得到AO=CO,然后证明△OAE≌△OCF(ASA),得到OE=OF,可得出结论.
证明 ∵∠AEF=∠EFC,∴AD∥BC.
∵AD=BC,∴四边形ABCD是平行四边形,∴AO=CO,
又∵AD∥BC,∴∠EAC=∠FCA,
在△OAE和△OCF中, ∴△OAE≌△OCF(ASA).∴OE=OF.
又∵AO=CO,∴四边形AFCE是平行四边形.
点拨 在应用对角线互相平分的四边形是平行四边形证明时,只说明一条对角线被另一条对角线平分就认为四边形是平行四边形是错误的.
经典例题
题型 平行四边形的判定与性质的综合运用
例 如图所示,已知D,E,F分别在△ABC的边BC,AB,AC上,且DE∥AF,DE=AF,将FD延长到点G,使FG=2DF,连接AG,则ED与AG互相平分吗?请说明理由.
分析 由一组对边平行且相等的四边形是平行四边形得四边形AEGD是平行四边形,即可得出结论.
分析 由一组对边平行且相等的四边形是平行四边形得四边形AEGD是平行四边形,即可得出结论.
解析 ED与AG互相平分.
理由:如图所示,连接EG,AD.
∵DE∥AF,DE=AF,∴四边形AEDF是平行四边形.
∴AE∥DF,AE=DF.
又∵FG=2DF,∴DG=DF.∴AE=DG.
又∵AE∥DG,∴四边形AEGD是平行四边形.∴ED与AG互相平分.
方法归纳 平行四边形的性质定理与判定定理是互逆的性质定理是已知平行四边形,从而得到对边相等、对角相等、对角线互相平分等结论;判定定理是由四边形的两组对边分别相等、两组对角分别相等、对角线互相平分等条件来证明这个四边形为平行四边形.
