3.5 相似三角形的应用 专项测试卷A 湖南省祁阳市浯溪二中2021-2022学年九年级数学上册(Word版含答案)
文档属性
| 名称 | 3.5 相似三角形的应用 专项测试卷A 湖南省祁阳市浯溪二中2021-2022学年九年级数学上册(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 656.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 10:21:41 | ||
图片预览




文档简介
祁阳市浯溪二中3.5《相似三角形的应用》专项测试卷A
一.选择题(每小题4分,共40分)
1.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=8m,则池塘的宽DE为( C )
A.32m B.36m C.48m D.56m
2.小兵身高1.4m,他的影长是2.1m,若此时学校旗杆的影长是12m,那么旗杆的高度( D )
A.4.5m B.6m C.7.2m D.8m
3.身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到AC=2米,CB=18米,则旗杆的高度是( C )
A.8米 B.14.4米 C.16米 D.20米
4.如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( C )平方米.
A.3 B.9 C.12 D.24
5.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
6.如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面1.7米,那么旗杆EF的高度为( )
A.10米 B.11.7米 C.米 D.米
7.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是( )
A.9.3m B.10.5m C.12.4m D.14m
8.中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
9.已知△ABC的三边长分别为20cm,50cm,60cm,现要利用长为40cm和60cm的两根铁丝绘制作与△ABC相似的三角形框架,如果以其中一根铁丝为一边,从另一根铁丝上截取两段(允许有余料)作为另外两边,可以作成不同的三角形框架有( )
A.1种 B.2种 C.3种 D.4种
10.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.18cm D.24cm
二.填空题(每小题4分,共40分)
1.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB= m.
12.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为 步.
13.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
14.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,且CE∥BD,并测得BC=4m,CA=1m,那么树BD的高度是 m.
15.如图,阳光通过窗口AB照到室内,在地面上留下一个亮区ED,已知亮区一边到窗下的墙脚距离CE=2.7m,窗高AB=0.8m,窗口底边离地面的高度BC=1m,则亮区宽度ED= m.
16.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20cm,到屏幕的距离为30cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 .
17.为了估算河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,然后再在河岸上选点E,使得EC⊥BC,设BC与AE交于点D,如图所示,测得BD=120米,DC=60米,EC=50米,那么这条河的大致宽度是 .
18.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为 步.
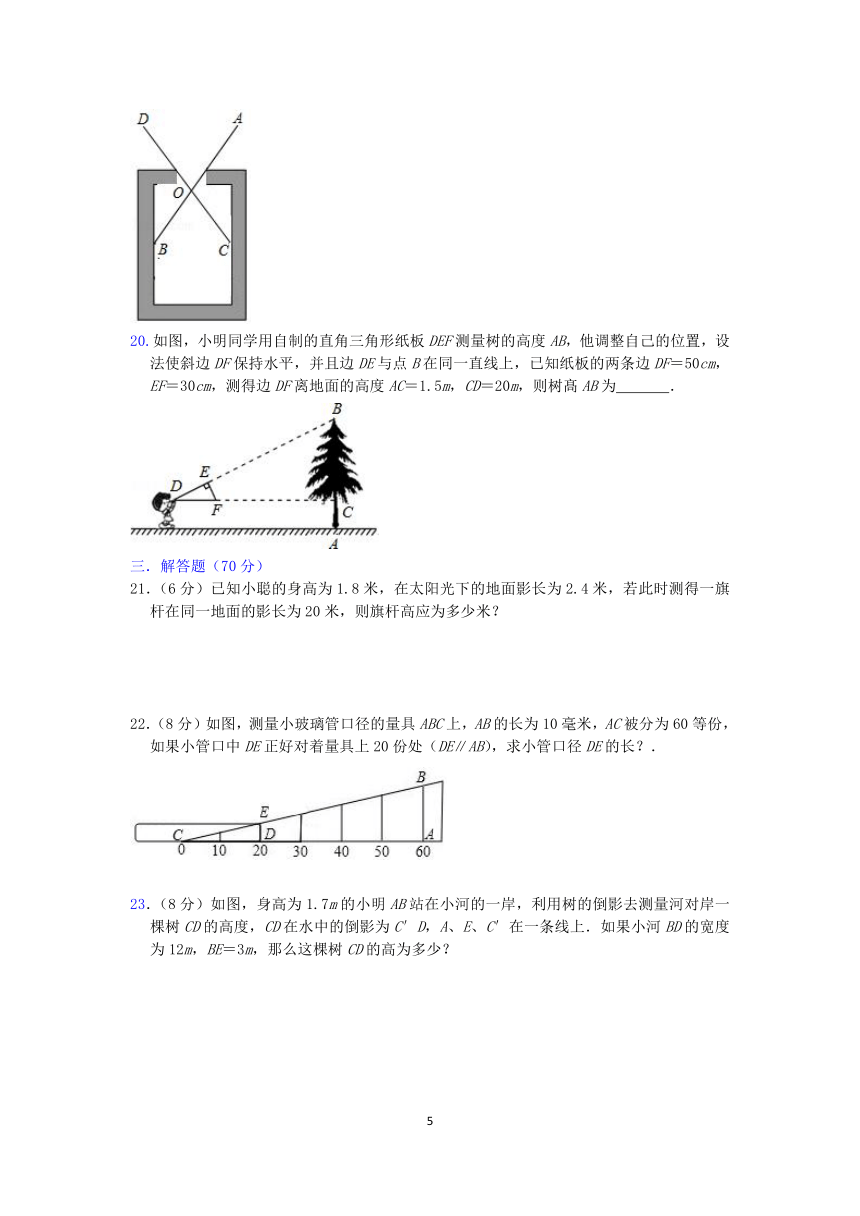
19.如图是用卡钳测量容器内径的示意图,现量的卡钳上A、D两端的距离为4cm,,则容器的内径BC= .
20.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树髙AB为 .
三.解答题(70分)
21.(6分)已知小聪的身高为1.8米,在太阳光下的地面影长为2.4米,若此时测得一旗杆在同一地面的影长为20米,则旗杆高应为多少米?
22.(8分)如图,测量小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DE∥AB),求小管口径DE的长?.
23.(8分)如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为多少?
参考答案
1.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=8m,则池塘的宽DE为( C )
A.32m B.36m C.48m D.56m
【分析】根据相似三角形的性质即可解决问题;【解答】解:∵AB∥DE,∴△ABC∽△DEC,∴=,∴=,∴DE=48m,故选:.
2.小兵身高1.4m,他的影长是2.1m,若此时学校旗杆的影长是12m,那么旗杆的高度( D )
A.4.5m B.6m C.7.2m D.8m
【分析】由于光线是平行的,影长都在地面上,那么可得身高与影长构成的三角形和旗杆和影长构成的三角形相似,利用对应边成比例可得旗杆的高度.
【解答】解:设旗杆的高度为xm,
根据题意得:,
解得:x=8,
即旗杆的高度为8m,
3.身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到AC=2米,CB=18米,则旗杆的高度是( C )
A.8米 B.14.4米 C.16米 D.20米
【分析】因为人和旗杆均垂直于地面,所以构成相似三角形,利用相似比解题即可.
【解答】解:设旗杆高度为h,
由题意得=,
解得:h=16米.
4.如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( C )平方米.
A.3 B.9 C.12 D.24
【分析】先根据相似三角形的判定定理得出△AMB∽△CBE,故可得出=的值,设CE=x,则BC=2x,在Rt△CBE中根据勾股定理求出x的值,故可得出CE,AB=BC,AM=2AB的值,再根据S草皮=S△CBE+S△AMB,即可得出结论.
【解答】解:∵△MDE是直角三角形,四边形ABCD是正方形,
∴∠MAB=∠BCE=90°,∠M+∠ABM=90°,∠ABM+∠CBE=90°,
∴∠M=∠CBE,
∴△AMB∽△CBE,
∴=,
∵MB=6,BE=4,
∴===,
∵AB=BC,
∴=,
设CE=2x,则BC=3x,在Rt△CBE中,
BE2=BC2+CE2,即42=(3x)2+(2x)2,解得x=,
∴CE=,AB=BC=,AM=AB=,
∴S草皮=S△CBE+S△AMB=××+××
=12.
5.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
【分析】根据同一时刻物高与影长成正比可得出结论.
【解答】解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴,解得x=45(尺).
故选:B.
6.如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面1.7米,那么旗杆EF的高度为( )
A.10米 B.11.7米 C.米 D.米
【分析】延长BD交EF于H,如图,利用四边形ABHF为矩形得到AF=BH=10,HF=AB=1.7,再利用△BCD为等腰直角三角形,可判断△BHE为等腰直角三角形,所以EH=BH=10,
然后计算EH+HF即可.
【解答】解:延长BD交EF于H,如图,
∵BD∥AF,EF⊥AF,
∴BH⊥EF,
易得四边形ABHF为矩形,
∴AF=BH=10,HF=AB=1.7,
∵△BCD为等腰直角三角形,
∴∠CBD=45°,
∴△BHE为等腰直角三角形,
∴EH=BH=10,
∴EF=EH+HF=10+1.7=11.7.
答:旗杆EF的高度为11.7m.
故选:B.
7.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是( )
A.9.3m B.10.5m C.12.4m D.14m
【分析】先证明△ABE∽△ACD,则利用相似三角形的性质得=,然后利用比例性质求出CD即可.
【解答】解:∵EB∥CD,
∴△ABE∽△ACD,
∴=,即=,
∴CD=10.5(米).
故选:B.
8.中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
【分析】由平行得相似,由相似得比例,即可作出判断.
【解答】解:∵EF∥AB,
∴△CEF∽△CAB,
∴==,
故选:B.
9.已知△ABC的三边长分别为20cm,50cm,60cm,现要利用长为40cm和60cm的两根铁丝绘制作与△ABC相似的三角形框架,如果以其中一根铁丝为一边,从另一根铁丝上截取两段(允许有余料)作为另外两边,可以作成不同的三角形框架有( )
A.1种 B.2种 C.3种 D.4种
【分析】若以40cm长的钢筋为短边,显然不成立,故有两种不同的截法:(1)以40cm长的钢筋为最长边,(2)以40cm长的钢筋为中边,根据相似三角形的三边对应成比例,列式计算.
【解答】解:有两种不同的截法:
(1)以40cm长的钢筋为最长边,设中边为y,短边长为x,
则有,==,
解得x=,y=,
所以从60cm长的钢筋上分别截取cm、cm的两段;
(2)以40cm长的钢筋为中边,
设长边为x,短边长为y,
==
解得x=,y=,x+y>60,不符合题意,
(3)以40cm长的钢筋为最短边,设长边为x,中边长为y,
==,
解得x=120,y=100,不合题意,
故选:A.
10.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.18cm D.24cm
【分析】根据题意可画出图形,再根据相似三角形的性质对应边成比例解答.
【解答】解:∵DE∥BC,
∴△AED∽△ABC
∴,
设屏幕上的小树高是x,则,
解得x=18cm.
故选:C.
二.填空题(每小题4分,共40分)
1.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB= 100 m.
【分析】由两角对应相等可得△BAD∽△CED,利用对应边成比例可得两岸间的大致距离AB.
【解答】解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得:AB=(米).
故答案为:100.
12.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为 步.
【分析】证明△CDK∽△DAH,利用相似三角形的性质得=,然后利用比例性质可求出CK的长.
【解答】解:DH=100,DK=100,AH=15,
∵AH∥DK,
∴∠CDK=∠A,
而∠CKD=∠AHD,
∴△CDK∽△DAH,
∴=,即=,
∴CK=.
答:KC的长为步.
故答案为.
13.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
【分析】如图1,根据正方形的性质得:DE∥BC,则△ADE∽△ACB,列比例式可得结论;如图2,同理可得正方形的边长,比较可得最大值.
【解答】解:如图1,∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=12﹣x,
∵DE∥CF,∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,∴,
∴,x=,
如图2,四边形DGFE是正方形,
过C作CP⊥AB于P,交DG于Q,
设ED=x,
S△ABC=AC BC=AB CP,
12×5=13CP,
CP=,
同理得:△CDG∽△CAB,∴,
∴,x=,
∴该直角三角形能容纳的正方形边长最大是(步),
故答案为:.
14.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,且CE∥BD,并测得BC=4m,CA=1m,那么树BD的高度是 10 m.
【分析】先根据相似三角形的判定定理得出Rt△ACE∽Rt△ABD,再根据相似三角形的对应边成比例即可求出BD的长.
【解答】解:∵EC∥AB,BD⊥AB,
∴EC∥BD,∠ACE=∠ABD=90°,
在Rt△ACE∽Rt△ABD中,∠A=∠A,∠ACE=∠ABD=90°,
∴Rt△ACE∽Rt△ABD,
∴,即,解得BD=10m.
故答案为:10
15.如图,阳光通过窗口AB照到室内,在地面上留下一个亮区ED,已知亮区一边到窗下的墙脚距离CE=2.7m,窗高AB=0.8m,窗口底边离地面的高度BC=1m,则亮区宽度ED= 1.2 m.
【分析】因为光线是平行的,所以将出现一组相似三角形,根据对应边成比例直接解答即可.
【解答】解:根据题意,易得△DCB∽△ACE,
∴=,
又因为AB=0.8米,CE=2.7米,BC=1米,
所以=,
解得ED=1.2米.
故答案为:1.2.
16.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20cm,到屏幕的距离为30cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 9cm .
【分析】根据题意可画出图形,再根据相似三角形的性质对应边成比例解答.
【解答】解:如图所示:∵DE∥BC,
∴△AED∽△ABC
∴=
设屏幕上的小树高是x,则=,
解得:x=9.
故答案为:9cm.
17.为了估算河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,然后再在河岸上选点E,使得EC⊥BC,设BC与AE交于点D,如图所示,测得BD=120米,DC=60米,EC=50米,那么这条河的大致宽度是 100米 .
【分析】先可证明△ADB∽△EDC,然后依据相似三角形的性质求解即可.
【解答】解:∵AB⊥BC,EC⊥BC,
∴∠B=∠C=90°.
又∵∠ADB=∠EDC,
∴△ADB∽△EDC.
∴,即.
解得:AB=100米.
故答案为:100米
18.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为 300 步.
【分析】设正方形城池的边长为x步,则AE=CE=x,证明Rt△BEA∽Rt△EDC,利用相似比得到=,然后利用比例性质求出x即可.
【解答】解:设正方形城池的边长为x步,则AE=CE=x,
∵AE∥CD,
∴∠BEA=∠EDC,
∴Rt△BEA∽Rt△EDC,
∴=,即=,
∴x=300,
即正方形城池的边长为300步.
故答案为300.
19.如图是用卡钳测量容器内径的示意图,现量的卡钳上A、D两端的距离为4cm,,则容器的内径BC= 8cm .
【分析】连接AD,BC,依题意得:△AOD∽△BOC,则其对应边成比例,由此求得BC的长度.
【解答】解:如图,连接AD,BC,
∵,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴==
又AD=4cm,
∴BC=2AD=8cm.
故答案是:8cm.
20.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树髙AB为 16.5m .
【分析】利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明同学的身高即可求得树高AB.
【解答】解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴=,
∵DF=50cm=0.5m,EF=30cm=0.3m,AC=1.5m,CD=20m,
∴由勾股定理求得DE=40cm,
∴=,
∴BC=15米,
∴AB=AC+BC=1.5+15=16.5(米).
故答案为:16.5m.
三.解答题(70分)
21.(6分)已知小聪的身高为1.8米,在太阳光下的地面影长为2.4米,若此时测得一旗杆在同一地面的影长为20米,则旗杆高应为多少米?
解:设旗杆高为xm,根据题意得,=,解得x=15m.
22.(8分)如图,测量小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DE∥AB),求小管口径DE的长?.
【分析】利用相似三角形的相似比,列出方程,通过解方程求出小管口径DE的长即可.
【解答】解:∵DE∥AB
∴△CDE∽△CAB
∴CD:CA=DE:AB
∴20:60=DE:10
∴DE=毫米
∴小管口径DE的长是毫米.
23.(8分)如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为多少?
【分析】首先判定△ABE∽△CDE,再根据相似三角形的性质可得=,然后再代入数据计算即可.
【解答】解:∵AB,CD均垂直于地面,所以AB∥CD,
∴△ABE∽△C′DE,
∵CD在水中的倒影为C′D,
∴△ABE∽△C′DE,
∴=,
又∵AB=1.7,BE=3,BD=12,
∴=,
∴CD=5.1,
24.(12分)数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.
25.(12分)如图,果果同学正向着教学楼(AB)走去,他发现教学楼后面有一座5G信号接收塔(CD),经过了解,教学楼、接收塔的高分别是21.6m和31.6m,它们之间的距离(BD)为30m,该同学的眼睛距地面高度(EF)是1.6m.当他刚发现接收塔的顶部C恰好被教学楼的顶部A挡住时,他与教学楼(AB)之间的距离为多少米?
26.(12分)真身宝塔,位于陕西省扶风法门镇法门寺内,因塔下藏有佛祖真身舍利而得名.小玲和晓静很想知道真身宝塔的高度PQ,于是,有一天,他们带着标杆和皮尺来到法门寺进行测量,测量方案如下:如图,首先,小玲在C处放置一平面镜,她从点C沿QC后退,当退行1.8米到B处时,恰好在镜子中看到塔顶P的像,此时测得小玲眼睛到地面的距离AB为1.5米;然后,晓静在F处竖立了一根高1.6米的标杆EF,发现地面上的点M、标杆顶点E和塔顶P在一条直线上,此时测得FM为2.4米,CF为11.7米,已知PQ⊥QM,AB⊥QM,EF⊥QM,点Q、C、B、F、M在一条直线上,请根据以上所测数据,计算真身宝塔的高度PQ.
27.(12分)有一块直角三角形木板,∠B=90°,AB=1.5m,BC=2m,要把它加工成一个面积尽可能大的正方形桌面.甲、乙两位同学的加工方法分别如图1、图2所示.请你用学过的知识说明哪位同学的加工方法更好(加工损耗忽略不计).
参考答案:
24.数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.
解:设广告牌的高度EF为xm,
依题意知:DB=11m,BG=2m,DH=1m,AB=CD=1.6m.
∴GD=DB﹣BG=9m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴=,即=.
∴=.
∴DF=x﹣1.
由平面镜反射规律可得:∠EGF=∠AGB.
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴=,即=.
∴=.
∴x=12.8.
故树的高度EF为12.8m.
25.如图,果果同学正向着教学楼(AB)走去,他发现教学楼后面有一座5G信号接收塔(CD),经过了解,教学楼、接收塔的高分别是21.6m和31.6m,它们之间的距离(BD)为30m,该同学的眼睛距地面高度(EF)是1.6m.当他刚发现接收塔的顶部C恰好被教学楼的顶部A挡住时,他与教学楼(AB)之间的距离为多少米?
解:如图,过E作EG⊥CD交AB于H,CD于G,
根据题意可得:四边形EFCG是矩形,
∴EF=HB=CG=1.6m,EH=FB,HG=BC=30m,
∴AH=20m,DG=30m,
∵AH∥DG,
∴△AEH∽△DEG,
∴=,
即=,
∴EH=60.
答:某同学与教学楼(AB)之间的距离为60米.
26.真身宝塔,位于陕西省扶风法门镇法门寺内,因塔下藏有佛祖真身舍利而得名.小玲和晓静很想知道真身宝塔的高度PQ,于是,有一天,他们带着标杆和皮尺来到法门寺进行测量,测量方案如下:如图,首先,小玲在C处放置一平面镜,她从点C沿QC后退,当退行1.8米到B处时,恰好在镜子中看到塔顶P的像,此时测得小玲眼睛到地面的距离AB为1.5米;然后,晓静在F处竖立了一根高1.6米的标杆EF,发现地面上的点M、标杆顶点E和塔顶P在一条直线上,此时测得FM为2.4米,CF为11.7米,已知PQ⊥QM,AB⊥QM,EF⊥QM,点Q、C、B、F、M在一条直线上,请根据以上所测数据,计算真身宝塔的高度PQ.
【考点】相似三角形的应用.
【分析】根据已知条件推出△PCQ∽△ACB,求得QC=1.2PQ,又根据相似三角形的性质得到,于是得到答案.
【解答】解:∵∠PQC=∠ABC=90°,∠PCQ=∠ACB,
∴△PCQ∽△ACB,
∴,∴,∴QC=1.2PQ,∵∠PQF=∠EFM=90°,∠PMQ=∠EMF,∴△PMQ∽△EMF,∴,∴,即,∴PQ=47,答:真身宝塔的高度PQ为47米.
27.有一块直角三角形木板,∠B=90°,AB=1.5m,BC=2m,要把它加工成一个面积尽可能大的正方形桌面.甲、乙两位同学的加工方法分别如图1、图2所示.请你用学过的知识说明哪位同学的加工方法更好(加工损耗忽略不计).
【考点】正方形的判定;相似三角形的应用.
【分析】利用相似三角形的性质分别求出正方形的边长,可得结论.
【解答】解:如图1所示,设甲同学加工的桌面边长为xm,
∵DE∥AB,
∴△CDE∽△CBA,
∴,
即,
∴x=.
如图2所示,过点B作BH⊥AC,交AC于点H,交DE于点P.
由勾股定理得:
AC=,
∵,
∴,
设乙同学加工的桌面边长为ym,
∵DE∥AC,
∴△BDE∽△BAC,
∴,
即,
∴y=,
∵>,即x>y,x2>y2,
∴甲同学的加工方法更好.
25
一.选择题(每小题4分,共40分)
1.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=8m,则池塘的宽DE为( C )
A.32m B.36m C.48m D.56m
2.小兵身高1.4m,他的影长是2.1m,若此时学校旗杆的影长是12m,那么旗杆的高度( D )
A.4.5m B.6m C.7.2m D.8m
3.身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到AC=2米,CB=18米,则旗杆的高度是( C )
A.8米 B.14.4米 C.16米 D.20米
4.如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( C )平方米.
A.3 B.9 C.12 D.24
5.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
6.如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面1.7米,那么旗杆EF的高度为( )
A.10米 B.11.7米 C.米 D.米
7.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是( )
A.9.3m B.10.5m C.12.4m D.14m
8.中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
9.已知△ABC的三边长分别为20cm,50cm,60cm,现要利用长为40cm和60cm的两根铁丝绘制作与△ABC相似的三角形框架,如果以其中一根铁丝为一边,从另一根铁丝上截取两段(允许有余料)作为另外两边,可以作成不同的三角形框架有( )
A.1种 B.2种 C.3种 D.4种
10.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.18cm D.24cm
二.填空题(每小题4分,共40分)
1.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB= m.
12.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为 步.
13.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
14.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,且CE∥BD,并测得BC=4m,CA=1m,那么树BD的高度是 m.
15.如图,阳光通过窗口AB照到室内,在地面上留下一个亮区ED,已知亮区一边到窗下的墙脚距离CE=2.7m,窗高AB=0.8m,窗口底边离地面的高度BC=1m,则亮区宽度ED= m.
16.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20cm,到屏幕的距离为30cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 .
17.为了估算河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,然后再在河岸上选点E,使得EC⊥BC,设BC与AE交于点D,如图所示,测得BD=120米,DC=60米,EC=50米,那么这条河的大致宽度是 .
18.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为 步.
19.如图是用卡钳测量容器内径的示意图,现量的卡钳上A、D两端的距离为4cm,,则容器的内径BC= .
20.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树髙AB为 .
三.解答题(70分)
21.(6分)已知小聪的身高为1.8米,在太阳光下的地面影长为2.4米,若此时测得一旗杆在同一地面的影长为20米,则旗杆高应为多少米?
22.(8分)如图,测量小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DE∥AB),求小管口径DE的长?.
23.(8分)如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为多少?
参考答案
1.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=8m,则池塘的宽DE为( C )
A.32m B.36m C.48m D.56m
【分析】根据相似三角形的性质即可解决问题;【解答】解:∵AB∥DE,∴△ABC∽△DEC,∴=,∴=,∴DE=48m,故选:.
2.小兵身高1.4m,他的影长是2.1m,若此时学校旗杆的影长是12m,那么旗杆的高度( D )
A.4.5m B.6m C.7.2m D.8m
【分析】由于光线是平行的,影长都在地面上,那么可得身高与影长构成的三角形和旗杆和影长构成的三角形相似,利用对应边成比例可得旗杆的高度.
【解答】解:设旗杆的高度为xm,
根据题意得:,
解得:x=8,
即旗杆的高度为8m,
3.身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到AC=2米,CB=18米,则旗杆的高度是( C )
A.8米 B.14.4米 C.16米 D.20米
【分析】因为人和旗杆均垂直于地面,所以构成相似三角形,利用相似比解题即可.
【解答】解:设旗杆高度为h,
由题意得=,
解得:h=16米.
4.如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( C )平方米.
A.3 B.9 C.12 D.24
【分析】先根据相似三角形的判定定理得出△AMB∽△CBE,故可得出=的值,设CE=x,则BC=2x,在Rt△CBE中根据勾股定理求出x的值,故可得出CE,AB=BC,AM=2AB的值,再根据S草皮=S△CBE+S△AMB,即可得出结论.
【解答】解:∵△MDE是直角三角形,四边形ABCD是正方形,
∴∠MAB=∠BCE=90°,∠M+∠ABM=90°,∠ABM+∠CBE=90°,
∴∠M=∠CBE,
∴△AMB∽△CBE,
∴=,
∵MB=6,BE=4,
∴===,
∵AB=BC,
∴=,
设CE=2x,则BC=3x,在Rt△CBE中,
BE2=BC2+CE2,即42=(3x)2+(2x)2,解得x=,
∴CE=,AB=BC=,AM=AB=,
∴S草皮=S△CBE+S△AMB=××+××
=12.
5.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
【分析】根据同一时刻物高与影长成正比可得出结论.
【解答】解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴,解得x=45(尺).
故选:B.
6.如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面1.7米,那么旗杆EF的高度为( )
A.10米 B.11.7米 C.米 D.米
【分析】延长BD交EF于H,如图,利用四边形ABHF为矩形得到AF=BH=10,HF=AB=1.7,再利用△BCD为等腰直角三角形,可判断△BHE为等腰直角三角形,所以EH=BH=10,
然后计算EH+HF即可.
【解答】解:延长BD交EF于H,如图,
∵BD∥AF,EF⊥AF,
∴BH⊥EF,
易得四边形ABHF为矩形,
∴AF=BH=10,HF=AB=1.7,
∵△BCD为等腰直角三角形,
∴∠CBD=45°,
∴△BHE为等腰直角三角形,
∴EH=BH=10,
∴EF=EH+HF=10+1.7=11.7.
答:旗杆EF的高度为11.7m.
故选:B.
7.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是( )
A.9.3m B.10.5m C.12.4m D.14m
【分析】先证明△ABE∽△ACD,则利用相似三角形的性质得=,然后利用比例性质求出CD即可.
【解答】解:∵EB∥CD,
∴△ABE∽△ACD,
∴=,即=,
∴CD=10.5(米).
故选:B.
8.中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
【分析】由平行得相似,由相似得比例,即可作出判断.
【解答】解:∵EF∥AB,
∴△CEF∽△CAB,
∴==,
故选:B.
9.已知△ABC的三边长分别为20cm,50cm,60cm,现要利用长为40cm和60cm的两根铁丝绘制作与△ABC相似的三角形框架,如果以其中一根铁丝为一边,从另一根铁丝上截取两段(允许有余料)作为另外两边,可以作成不同的三角形框架有( )
A.1种 B.2种 C.3种 D.4种
【分析】若以40cm长的钢筋为短边,显然不成立,故有两种不同的截法:(1)以40cm长的钢筋为最长边,(2)以40cm长的钢筋为中边,根据相似三角形的三边对应成比例,列式计算.
【解答】解:有两种不同的截法:
(1)以40cm长的钢筋为最长边,设中边为y,短边长为x,
则有,==,
解得x=,y=,
所以从60cm长的钢筋上分别截取cm、cm的两段;
(2)以40cm长的钢筋为中边,
设长边为x,短边长为y,
==
解得x=,y=,x+y>60,不符合题意,
(3)以40cm长的钢筋为最短边,设长边为x,中边长为y,
==,
解得x=120,y=100,不合题意,
故选:A.
10.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.18cm D.24cm
【分析】根据题意可画出图形,再根据相似三角形的性质对应边成比例解答.
【解答】解:∵DE∥BC,
∴△AED∽△ABC
∴,
设屏幕上的小树高是x,则,
解得x=18cm.
故选:C.
二.填空题(每小题4分,共40分)
1.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB= 100 m.
【分析】由两角对应相等可得△BAD∽△CED,利用对应边成比例可得两岸间的大致距离AB.
【解答】解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得:AB=(米).
故答案为:100.
12.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为 步.
【分析】证明△CDK∽△DAH,利用相似三角形的性质得=,然后利用比例性质可求出CK的长.
【解答】解:DH=100,DK=100,AH=15,
∵AH∥DK,
∴∠CDK=∠A,
而∠CKD=∠AHD,
∴△CDK∽△DAH,
∴=,即=,
∴CK=.
答:KC的长为步.
故答案为.
13.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
【分析】如图1,根据正方形的性质得:DE∥BC,则△ADE∽△ACB,列比例式可得结论;如图2,同理可得正方形的边长,比较可得最大值.
【解答】解:如图1,∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=12﹣x,
∵DE∥CF,∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,∴,
∴,x=,
如图2,四边形DGFE是正方形,
过C作CP⊥AB于P,交DG于Q,
设ED=x,
S△ABC=AC BC=AB CP,
12×5=13CP,
CP=,
同理得:△CDG∽△CAB,∴,
∴,x=,
∴该直角三角形能容纳的正方形边长最大是(步),
故答案为:.
14.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,且CE∥BD,并测得BC=4m,CA=1m,那么树BD的高度是 10 m.
【分析】先根据相似三角形的判定定理得出Rt△ACE∽Rt△ABD,再根据相似三角形的对应边成比例即可求出BD的长.
【解答】解:∵EC∥AB,BD⊥AB,
∴EC∥BD,∠ACE=∠ABD=90°,
在Rt△ACE∽Rt△ABD中,∠A=∠A,∠ACE=∠ABD=90°,
∴Rt△ACE∽Rt△ABD,
∴,即,解得BD=10m.
故答案为:10
15.如图,阳光通过窗口AB照到室内,在地面上留下一个亮区ED,已知亮区一边到窗下的墙脚距离CE=2.7m,窗高AB=0.8m,窗口底边离地面的高度BC=1m,则亮区宽度ED= 1.2 m.
【分析】因为光线是平行的,所以将出现一组相似三角形,根据对应边成比例直接解答即可.
【解答】解:根据题意,易得△DCB∽△ACE,
∴=,
又因为AB=0.8米,CE=2.7米,BC=1米,
所以=,
解得ED=1.2米.
故答案为:1.2.
16.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20cm,到屏幕的距离为30cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 9cm .
【分析】根据题意可画出图形,再根据相似三角形的性质对应边成比例解答.
【解答】解:如图所示:∵DE∥BC,
∴△AED∽△ABC
∴=
设屏幕上的小树高是x,则=,
解得:x=9.
故答案为:9cm.
17.为了估算河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,然后再在河岸上选点E,使得EC⊥BC,设BC与AE交于点D,如图所示,测得BD=120米,DC=60米,EC=50米,那么这条河的大致宽度是 100米 .
【分析】先可证明△ADB∽△EDC,然后依据相似三角形的性质求解即可.
【解答】解:∵AB⊥BC,EC⊥BC,
∴∠B=∠C=90°.
又∵∠ADB=∠EDC,
∴△ADB∽△EDC.
∴,即.
解得:AB=100米.
故答案为:100米
18.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为 300 步.
【分析】设正方形城池的边长为x步,则AE=CE=x,证明Rt△BEA∽Rt△EDC,利用相似比得到=,然后利用比例性质求出x即可.
【解答】解:设正方形城池的边长为x步,则AE=CE=x,
∵AE∥CD,
∴∠BEA=∠EDC,
∴Rt△BEA∽Rt△EDC,
∴=,即=,
∴x=300,
即正方形城池的边长为300步.
故答案为300.
19.如图是用卡钳测量容器内径的示意图,现量的卡钳上A、D两端的距离为4cm,,则容器的内径BC= 8cm .
【分析】连接AD,BC,依题意得:△AOD∽△BOC,则其对应边成比例,由此求得BC的长度.
【解答】解:如图,连接AD,BC,
∵,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴==
又AD=4cm,
∴BC=2AD=8cm.
故答案是:8cm.
20.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树髙AB为 16.5m .
【分析】利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明同学的身高即可求得树高AB.
【解答】解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴=,
∵DF=50cm=0.5m,EF=30cm=0.3m,AC=1.5m,CD=20m,
∴由勾股定理求得DE=40cm,
∴=,
∴BC=15米,
∴AB=AC+BC=1.5+15=16.5(米).
故答案为:16.5m.
三.解答题(70分)
21.(6分)已知小聪的身高为1.8米,在太阳光下的地面影长为2.4米,若此时测得一旗杆在同一地面的影长为20米,则旗杆高应为多少米?
解:设旗杆高为xm,根据题意得,=,解得x=15m.
22.(8分)如图,测量小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DE∥AB),求小管口径DE的长?.
【分析】利用相似三角形的相似比,列出方程,通过解方程求出小管口径DE的长即可.
【解答】解:∵DE∥AB
∴△CDE∽△CAB
∴CD:CA=DE:AB
∴20:60=DE:10
∴DE=毫米
∴小管口径DE的长是毫米.
23.(8分)如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为多少?
【分析】首先判定△ABE∽△CDE,再根据相似三角形的性质可得=,然后再代入数据计算即可.
【解答】解:∵AB,CD均垂直于地面,所以AB∥CD,
∴△ABE∽△C′DE,
∵CD在水中的倒影为C′D,
∴△ABE∽△C′DE,
∴=,
又∵AB=1.7,BE=3,BD=12,
∴=,
∴CD=5.1,
24.(12分)数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.
25.(12分)如图,果果同学正向着教学楼(AB)走去,他发现教学楼后面有一座5G信号接收塔(CD),经过了解,教学楼、接收塔的高分别是21.6m和31.6m,它们之间的距离(BD)为30m,该同学的眼睛距地面高度(EF)是1.6m.当他刚发现接收塔的顶部C恰好被教学楼的顶部A挡住时,他与教学楼(AB)之间的距离为多少米?
26.(12分)真身宝塔,位于陕西省扶风法门镇法门寺内,因塔下藏有佛祖真身舍利而得名.小玲和晓静很想知道真身宝塔的高度PQ,于是,有一天,他们带着标杆和皮尺来到法门寺进行测量,测量方案如下:如图,首先,小玲在C处放置一平面镜,她从点C沿QC后退,当退行1.8米到B处时,恰好在镜子中看到塔顶P的像,此时测得小玲眼睛到地面的距离AB为1.5米;然后,晓静在F处竖立了一根高1.6米的标杆EF,发现地面上的点M、标杆顶点E和塔顶P在一条直线上,此时测得FM为2.4米,CF为11.7米,已知PQ⊥QM,AB⊥QM,EF⊥QM,点Q、C、B、F、M在一条直线上,请根据以上所测数据,计算真身宝塔的高度PQ.
27.(12分)有一块直角三角形木板,∠B=90°,AB=1.5m,BC=2m,要把它加工成一个面积尽可能大的正方形桌面.甲、乙两位同学的加工方法分别如图1、图2所示.请你用学过的知识说明哪位同学的加工方法更好(加工损耗忽略不计).
参考答案:
24.数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.
解:设广告牌的高度EF为xm,
依题意知:DB=11m,BG=2m,DH=1m,AB=CD=1.6m.
∴GD=DB﹣BG=9m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴=,即=.
∴=.
∴DF=x﹣1.
由平面镜反射规律可得:∠EGF=∠AGB.
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴=,即=.
∴=.
∴x=12.8.
故树的高度EF为12.8m.
25.如图,果果同学正向着教学楼(AB)走去,他发现教学楼后面有一座5G信号接收塔(CD),经过了解,教学楼、接收塔的高分别是21.6m和31.6m,它们之间的距离(BD)为30m,该同学的眼睛距地面高度(EF)是1.6m.当他刚发现接收塔的顶部C恰好被教学楼的顶部A挡住时,他与教学楼(AB)之间的距离为多少米?
解:如图,过E作EG⊥CD交AB于H,CD于G,
根据题意可得:四边形EFCG是矩形,
∴EF=HB=CG=1.6m,EH=FB,HG=BC=30m,
∴AH=20m,DG=30m,
∵AH∥DG,
∴△AEH∽△DEG,
∴=,
即=,
∴EH=60.
答:某同学与教学楼(AB)之间的距离为60米.
26.真身宝塔,位于陕西省扶风法门镇法门寺内,因塔下藏有佛祖真身舍利而得名.小玲和晓静很想知道真身宝塔的高度PQ,于是,有一天,他们带着标杆和皮尺来到法门寺进行测量,测量方案如下:如图,首先,小玲在C处放置一平面镜,她从点C沿QC后退,当退行1.8米到B处时,恰好在镜子中看到塔顶P的像,此时测得小玲眼睛到地面的距离AB为1.5米;然后,晓静在F处竖立了一根高1.6米的标杆EF,发现地面上的点M、标杆顶点E和塔顶P在一条直线上,此时测得FM为2.4米,CF为11.7米,已知PQ⊥QM,AB⊥QM,EF⊥QM,点Q、C、B、F、M在一条直线上,请根据以上所测数据,计算真身宝塔的高度PQ.
【考点】相似三角形的应用.
【分析】根据已知条件推出△PCQ∽△ACB,求得QC=1.2PQ,又根据相似三角形的性质得到,于是得到答案.
【解答】解:∵∠PQC=∠ABC=90°,∠PCQ=∠ACB,
∴△PCQ∽△ACB,
∴,∴,∴QC=1.2PQ,∵∠PQF=∠EFM=90°,∠PMQ=∠EMF,∴△PMQ∽△EMF,∴,∴,即,∴PQ=47,答:真身宝塔的高度PQ为47米.
27.有一块直角三角形木板,∠B=90°,AB=1.5m,BC=2m,要把它加工成一个面积尽可能大的正方形桌面.甲、乙两位同学的加工方法分别如图1、图2所示.请你用学过的知识说明哪位同学的加工方法更好(加工损耗忽略不计).
【考点】正方形的判定;相似三角形的应用.
【分析】利用相似三角形的性质分别求出正方形的边长,可得结论.
【解答】解:如图1所示,设甲同学加工的桌面边长为xm,
∵DE∥AB,
∴△CDE∽△CBA,
∴,
即,
∴x=.
如图2所示,过点B作BH⊥AC,交AC于点H,交DE于点P.
由勾股定理得:
AC=,
∵,
∴,
设乙同学加工的桌面边长为ym,
∵DE∥AC,
∴△BDE∽△BAC,
∴,
即,
∴y=,
∵>,即x>y,x2>y2,
∴甲同学的加工方法更好.
25
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
