湘教版数学七年级上册4.2线段、射线、直线 第2课时 课件(共23张PPT)
文档属性
| 名称 | 湘教版数学七年级上册4.2线段、射线、直线 第2课时 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 810.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 23:03:59 | ||
图片预览



文档简介
(共23张PPT)
4.2 线段、射线、直线
第2课时 线段的长短比较
温故知新
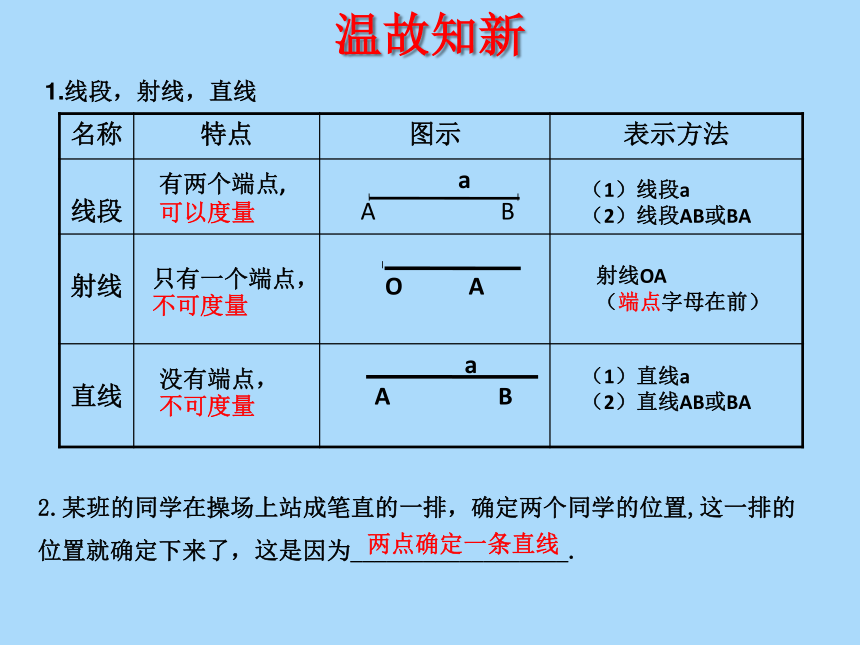
1.线段,射线,直线
名称 特点 图示 表示方法
线段 a A B
射线 O A
直线 a A B
有两个端点,可以度量
(1)线段a
(2)线段AB或BA
只有一个端点,不可度量
没有端点,不可度量
射线OA
(端点字母在前)
(1)直线a
(2)直线AB或BA
2.某班的同学在操场上站成笔直的一排,确定两个同学的位置,这一排的位置就确定下来了,这是因为__________________.
两点确定一条直线
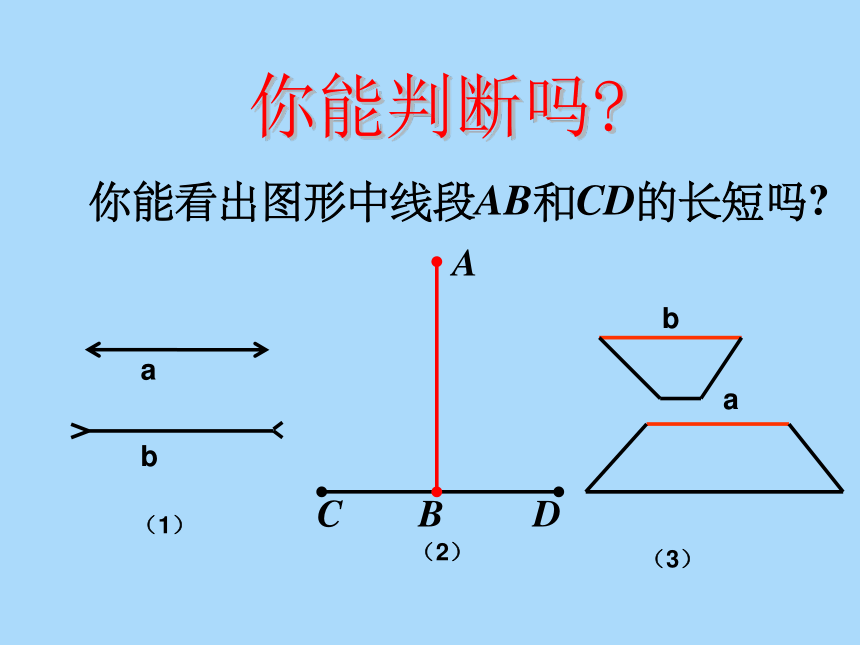
你能看出图形中线段AB和CD的长短吗
D
A
你能判断吗
C
B
(1)
a
b
(3)
a
b
(2)
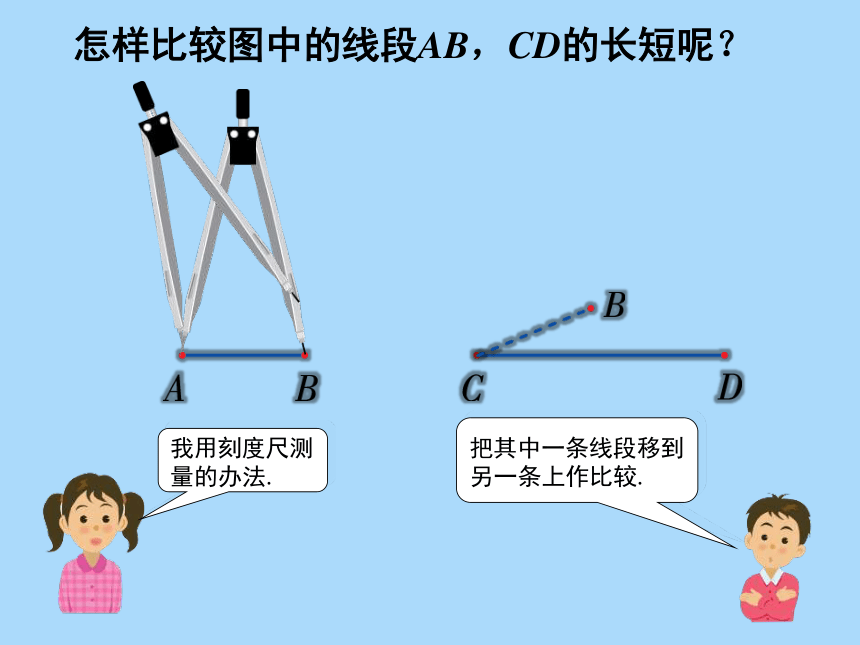
怎样比较图中的线段AB,CD的长短呢?
我用刻度尺测量的办法.
把其中一条线段移到另一条上作比较.
问题一:线段的长短比较
方法一:度量法
方法二:叠合法
(数)
(形)
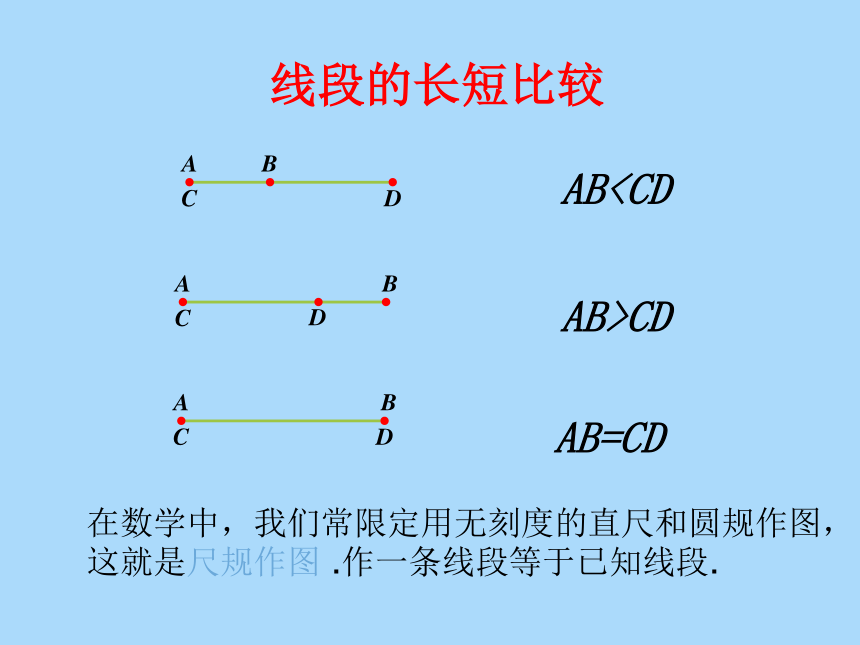
线段的长短比较
AB>CD
ABAB=CD
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图 .作一条线段等于已知线段.
C
A
D
B
C
A
D
B
C
A
D
B
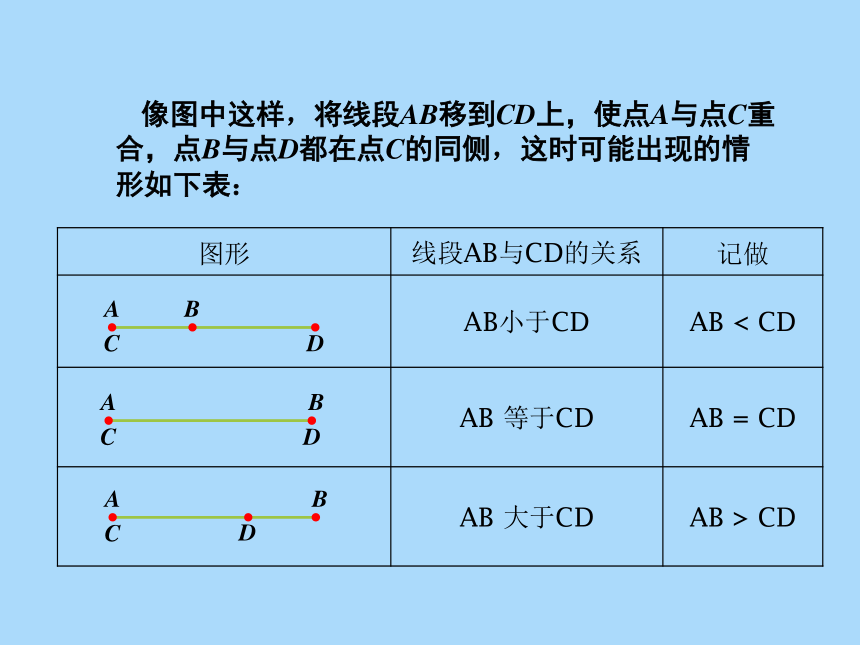
像图中这样,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,这时可能出现的情形如下表:
图形 线段AB与CD的关系 记做
AB小于CD AB < CD
AB 等于CD AB = CD
AB 大于CD AB > CD
C
A
D
B
C
A
D
B
C
A
D
B
如图,点C 落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,
A
B
C
a
设AB=a ,AC=b, BC=c ,
则线段AC就是a与c的和,记做b = a + c ;
c
b
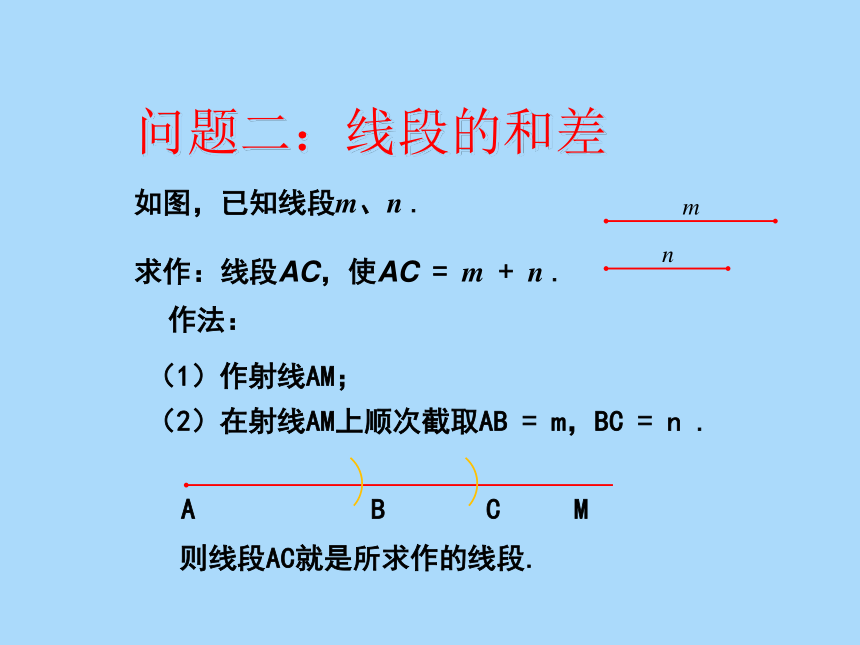
如图,已知线段m、n .
求作:线段AC,使AC = m + n .
m
n
作法:
(1)作射线AM;
A
M
B
C
则线段AC就是所求作的线段.
(2)在射线AM上顺次截取AB = m,BC = n .
问题二:线段的和差
如图,已知线段m、n .
求作:线段AC,使AC = m – n .
m
n
作法:
(1)作射线AM;
A
M
(2)在射线AM上截取AB = m ;
B
(3)在线段AB上截取BC = n .
C
则线段AC就是所求作的线段.
AB=
符号语言:
BC=
AC=
BC+AC
AB-AC
AB-BC
A
B
C
1、如图,C,D是线段AB上不同的两点,那么
(1)AB=____+____+____
(2)AC=____- DC, BD=____- CD
(3)AC=____- BC, BD=____- AD
A C D B
AC
DB
AD
BC
AB
CD
AB
【填一填】
2、点A,B,C 在同一条直线上,AB=5 cm,BC=3 cm,AC=_____.
解:⑴当C在线段AB上时,AC=______;
(2)当C在线段AB的延长线上时,AC=_____.
8 cm
2 cm
A
B
问题三:线段的中点
点C 把线段AB分成相等的两条线段AC与BC,点C 叫做线段AB 的中点。
记作:AC=CB=
A C B
AB,
AB=
2AC=2CB
A C B
类似地,还有线段的三等分点,四等分点等
A M N B
AB,
AB=
3AM=3MN=3NB
AM= MN=NB=
记作:
A M B N C
若AB=a,BC=b 呢?
问题四:线段的计算
如图,点A、B、C在一条直线上,AB=3cm,BC=1cm,M是AB 的中点,N是BC 的中点,求MN 的长.
【课堂练习】
例1.如图,点C是线段AB的中点
(1)若AB=6cm,则AC= cm.
(2)若AC=6cm,则AB= cm.
3
12
例2.已知:AD=4 cm,BD=2 cm,C为AB的中点,
则BC=_____ cm.
3
例3 如图,在直线上有A,B,C三点,AB=5 cm,BC=4 cm,如果O是线段AC的中点,求线段OB的长度.
解: ∵ AB=5 cm,BC=4 cm,
∴ AC=AB+ BC=9 cm.
又∵点O是线段AC的中点,
∴ OC= AC=4.5 cm.
∴ OB=OC-BC=4.5-4=0.5(cm).
例4.如图,线段ab=10 cm,点c是ab的中点,点d是ac的中点,点e是cb的中点,求线段de的长度.
解: ∵点C是AB的中点,且AB=10 cm
∴ AC=BC= AB=5 cm,
又∵点D是AC的中点
∴ DC= AC=2.5 cm,
又∵点E是CB的中点
∴ EC= CB=2.5 cm,
∴ DE=DC+CE=2.5 cm+2.5 cm=5 cm.
A
B
C
D
E
线段的长短比较
线段的和差(尺规作图)
线段的中点
度量、叠合
图形语言、文字语言、符号语言
描 述
方
法
方
法
【课堂小结】
你还有其他的收获与困惑吗?
本节课你有哪些收获?
【课堂小结】
谢谢大家的聆听!
4.2 线段、射线、直线
第2课时 线段的长短比较
温故知新
1.线段,射线,直线
名称 特点 图示 表示方法
线段 a A B
射线 O A
直线 a A B
有两个端点,可以度量
(1)线段a
(2)线段AB或BA
只有一个端点,不可度量
没有端点,不可度量
射线OA
(端点字母在前)
(1)直线a
(2)直线AB或BA
2.某班的同学在操场上站成笔直的一排,确定两个同学的位置,这一排的位置就确定下来了,这是因为__________________.
两点确定一条直线
你能看出图形中线段AB和CD的长短吗
D
A
你能判断吗
C
B
(1)
a
b
(3)
a
b
(2)
怎样比较图中的线段AB,CD的长短呢?
我用刻度尺测量的办法.
把其中一条线段移到另一条上作比较.
问题一:线段的长短比较
方法一:度量法
方法二:叠合法
(数)
(形)
线段的长短比较
AB>CD
AB
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图 .作一条线段等于已知线段.
C
A
D
B
C
A
D
B
C
A
D
B
像图中这样,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,这时可能出现的情形如下表:
图形 线段AB与CD的关系 记做
AB小于CD AB < CD
AB 等于CD AB = CD
AB 大于CD AB > CD
C
A
D
B
C
A
D
B
C
A
D
B
如图,点C 落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,
A
B
C
a
设AB=a ,AC=b, BC=c ,
则线段AC就是a与c的和,记做b = a + c ;
c
b
如图,已知线段m、n .
求作:线段AC,使AC = m + n .
m
n
作法:
(1)作射线AM;
A
M
B
C
则线段AC就是所求作的线段.
(2)在射线AM上顺次截取AB = m,BC = n .
问题二:线段的和差
如图,已知线段m、n .
求作:线段AC,使AC = m – n .
m
n
作法:
(1)作射线AM;
A
M
(2)在射线AM上截取AB = m ;
B
(3)在线段AB上截取BC = n .
C
则线段AC就是所求作的线段.
AB=
符号语言:
BC=
AC=
BC+AC
AB-AC
AB-BC
A
B
C
1、如图,C,D是线段AB上不同的两点,那么
(1)AB=____+____+____
(2)AC=____- DC, BD=____- CD
(3)AC=____- BC, BD=____- AD
A C D B
AC
DB
AD
BC
AB
CD
AB
【填一填】
2、点A,B,C 在同一条直线上,AB=5 cm,BC=3 cm,AC=_____.
解:⑴当C在线段AB上时,AC=______;
(2)当C在线段AB的延长线上时,AC=_____.
8 cm
2 cm
A
B
问题三:线段的中点
点C 把线段AB分成相等的两条线段AC与BC,点C 叫做线段AB 的中点。
记作:AC=CB=
A C B
AB,
AB=
2AC=2CB
A C B
类似地,还有线段的三等分点,四等分点等
A M N B
AB,
AB=
3AM=3MN=3NB
AM= MN=NB=
记作:
A M B N C
若AB=a,BC=b 呢?
问题四:线段的计算
如图,点A、B、C在一条直线上,AB=3cm,BC=1cm,M是AB 的中点,N是BC 的中点,求MN 的长.
【课堂练习】
例1.如图,点C是线段AB的中点
(1)若AB=6cm,则AC= cm.
(2)若AC=6cm,则AB= cm.
3
12
例2.已知:AD=4 cm,BD=2 cm,C为AB的中点,
则BC=_____ cm.
3
例3 如图,在直线上有A,B,C三点,AB=5 cm,BC=4 cm,如果O是线段AC的中点,求线段OB的长度.
解: ∵ AB=5 cm,BC=4 cm,
∴ AC=AB+ BC=9 cm.
又∵点O是线段AC的中点,
∴ OC= AC=4.5 cm.
∴ OB=OC-BC=4.5-4=0.5(cm).
例4.如图,线段ab=10 cm,点c是ab的中点,点d是ac的中点,点e是cb的中点,求线段de的长度.
解: ∵点C是AB的中点,且AB=10 cm
∴ AC=BC= AB=5 cm,
又∵点D是AC的中点
∴ DC= AC=2.5 cm,
又∵点E是CB的中点
∴ EC= CB=2.5 cm,
∴ DE=DC+CE=2.5 cm+2.5 cm=5 cm.
A
B
C
D
E
线段的长短比较
线段的和差(尺规作图)
线段的中点
度量、叠合
图形语言、文字语言、符号语言
描 述
方
法
方
法
【课堂小结】
你还有其他的收获与困惑吗?
本节课你有哪些收获?
【课堂小结】
谢谢大家的聆听!
同课章节目录
