2021-2022学年安徽省合肥三十中九年级(上)期中数学模拟练习试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年安徽省合肥三十中九年级(上)期中数学模拟练习试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 437.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 09:13:52 | ||
图片预览



文档简介
2021-2022学年安徽省合肥三十中九年级(上)期中数学模拟练习试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)抛物线y=﹣(x+1)2﹣3的顶点坐标是( )
A.(﹣1,﹣3) B.(﹣1,3) C.(1,﹣3) D.(1,3)
2.(4分)已知二次函数的图象与x轴有两个交点,且顶点坐标为(﹣2,1).若函数图象经过(1,y1),(﹣1,y2),(﹣4,y3)三点,则( )
A.y1<y3<y2 B.y2<y1<y3 C.y1<y2<y3 D.y2<y3<y1
3.(4分)关于二次函数y=x2+2x﹣8,下列说法正确的是( )
A.图象的对称轴在y轴的右侧
B.图象与y轴的交点坐标为(0,8)
C.图象与x轴的交点坐标为(﹣2,0)和(4,0)
D.y的最小值为﹣9
4.(4分)已知二次函数y=﹣(x+a)2﹣b的图象如图所示,则反比例函数与一次函数y=ax+b的图象可能是( )
A. B.
C. D.
5.(4分)如图所示,已知点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC的长约为( )
A.1.543 B.1.236 C.1.123 D.1.618
6.(4分)如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP B.△APD∽△PGD C.△APG∽△BFP D.△PCF∽△BCP
7.(4分)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:①该抛物线的开口向下;②该抛物线的顶点坐标为(1,5);③当x>2时,y随x的增大而减少;④3是方程ax2+bx+c=x的一个根.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
8.(4分)如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,点C距灯柱AB的水平距离为1.6米,点C距水平地面的距离为2.5米,灯罩D距灯柱AB的水平距离为3.2米,灯柱AB=1.5米,则灯罩D到水平地面的距离为( )
A.1.5米 B.1米 C.1.2米 D.1.4米
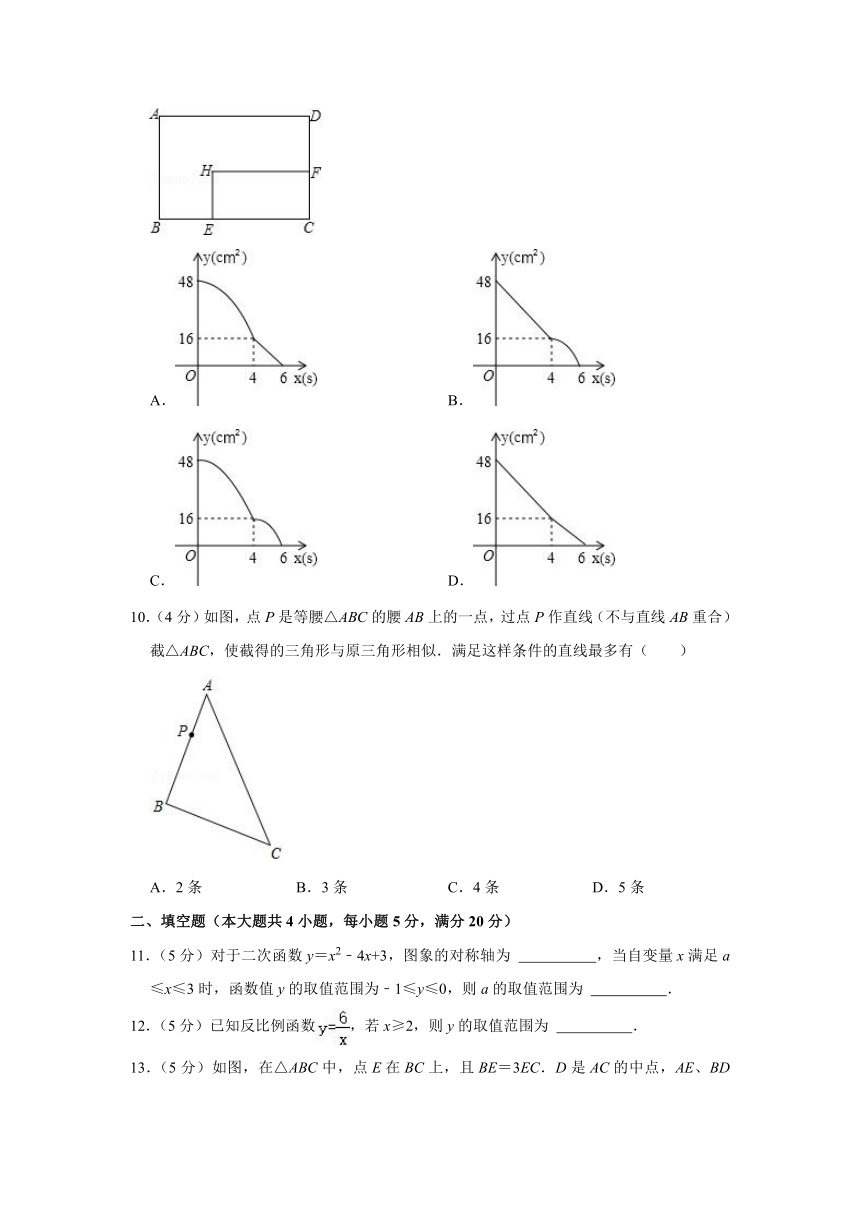
9.(4分)矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A. B.
C. D.
10.(4分)如图,点P是等腰△ABC的腰AB上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
二、填空题(本大题共4小题,每小题5分,满分20分)
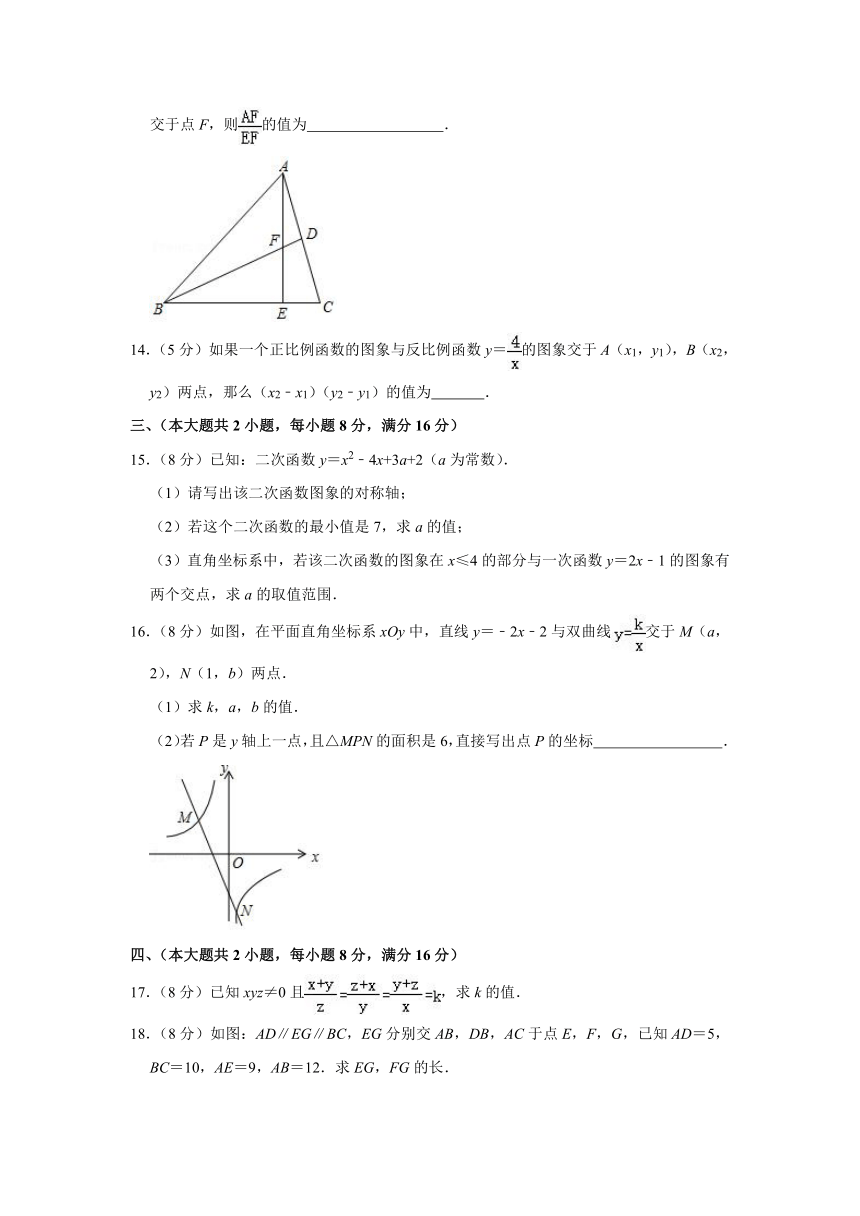
11.(5分)对于二次函数y=x2﹣4x+3,图象的对称轴为 ,当自变量x满足a≤x≤3时,函数值y的取值范围为﹣1≤y≤0,则a的取值范围为 .
12.(5分)已知反比例函数,若x≥2,则y的取值范围为 .
13.(5分)如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
14.(5分)如果一个正比例函数的图象与反比例函数y=的图象交于A(x1,y1),B(x2,y2)两点,那么(x2﹣x1)(y2﹣y1)的值为 .
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知:二次函数y=x2﹣4x+3a+2(a为常数).
(1)请写出该二次函数图象的对称轴;
(2)若这个二次函数的最小值是7,求a的值;
(3)直角坐标系中,若该二次函数的图象在x≤4的部分与一次函数y=2x﹣1的图象有两个交点,求a的取值范围.
16.(8分)如图,在平面直角坐标系xOy中,直线y=﹣2x﹣2与双曲线交于M(a,2),N(1,b)两点.
(1)求k,a,b的值.
(2)若P是y轴上一点,且△MPN的面积是6,直接写出点P的坐标 .
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)已知xyz≠0且,求k的值.
18.(8分)如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)新冠肺炎疫情期间,某药店进了一批口罩,每包进价10元,每包销售价定为25元时,每天销售1000包.经一段时间调查,发现每包销售单价每上涨1元,每天就少卖40包.其销售单价不低于进价,销售利润率不高于180%.设每包销售价为x元(x为正整数).
(1)请直接写出x的取值范围.
(2)设每天的总利润为w元,当每包销售价定为多少元时,该药店每天的利润最大?最大利润是多少元?
20.(10分)如图,点M是AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)求证:△AMF∽△BGM;
(2)请你再写出两对相似三角形.
六、(本题满分12分)
21.(12分)已知抛物线y=ax2+2ax+3a2﹣4(a≠0).
(1)该抛物线的对称轴为 ;
(2)若该抛物线的顶点在x轴上,求抛物线的解析式;
(3)设点M(m,y1),N(2,y2)在该抛物线上,若y1>y2,求m的取值范围.
七、(本题满分12分)
22.(12分)如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+6﹣>0的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
八、(本题满分14分)
23.(14分)某服装批发市场销售一种衬衫,衬衫每件进货价为50元.规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求出y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价?
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的50%,设销售这种衬衫每月的总利润为w(元),求w与x之间的函数关系式,x为多少时,w有最大值,最大利润是多少?
2021-2022学年安徽省合肥三十中九年级(上)期中数学模拟练习试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)抛物线y=﹣(x+1)2﹣3的顶点坐标是( )
A.(﹣1,﹣3) B.(﹣1,3) C.(1,﹣3) D.(1,3)
【分析】直接利用顶点式的特点可知顶点坐标.
【解答】解:抛物线y=﹣(x+1)2﹣3的顶点坐标是(﹣1,﹣3)
故选:A.
2.(4分)已知二次函数的图象与x轴有两个交点,且顶点坐标为(﹣2,1).若函数图象经过(1,y1),(﹣1,y2),(﹣4,y3)三点,则( )
A.y1<y3<y2 B.y2<y1<y3 C.y1<y2<y3 D.y2<y3<y1
【分析】先判断出二次函数的开口方向,再求出点(1,y1),(﹣1,y2),(﹣4,y3)到对称轴的距离,然后根据二次函数增减性判断即可.
【解答】解:∵图象与x轴有两个交点,且顶点坐标为(﹣2,1).
∴对称轴为直线x=﹣2,开口向下,
∵(1,y1),(﹣1,y2),(﹣4,y3)与对称轴的距离y2最近,y3最远,
∴y1<y3<y2.
故选:A.
3.(4分)关于二次函数y=x2+2x﹣8,下列说法正确的是( )
A.图象的对称轴在y轴的右侧
B.图象与y轴的交点坐标为(0,8)
C.图象与x轴的交点坐标为(﹣2,0)和(4,0)
D.y的最小值为﹣9
【分析】根据题目中的函数解析式和二次函数的性质,可以判断各个选项中的结论是否正确,从而可以解答本题.
【解答】解:∵二次函数y=x2+2x﹣8=(x+1)2﹣9=(x+4)(x﹣2),
∴该函数的对称轴是直线x=﹣1,在y轴的左侧,故选项A错误;
当x=0时,y=﹣8,即该函数与y轴交于点(0,﹣8),故选项B错误;
当y=0时,x=2或x=﹣4,即图象与x轴的交点坐标为(2,0)和(﹣4,0),故选项C错误;
当x=﹣1时,该函数取得最小值y=﹣9,故选项D正确;
故选:D.
4.(4分)已知二次函数y=﹣(x+a)2﹣b的图象如图所示,则反比例函数与一次函数y=ax+b的图象可能是( )
A. B.
C. D.
【分析】观察二次函数图象,找出a<0,b>0,再结合反比例(一次)函数图象与系数的关系,即可得出结论.
【解答】解:观察二次函数图象,发现:抛物线的顶点坐标在第四象限,开口向下,对称在y轴右侧,
∴﹣a>0,﹣b<0,
∴a<0,b>0.
∵反比例函数中ab<0,
∴反比例函数图象在第二、四象限;
∵一次函数y=ax+b,a<0,b>0,
∴一次函数y=ax+b的图象过第一、二、四象限.
故选:D.
5.(4分)如图所示,已知点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC的长约为( )
A.1.543 B.1.236 C.1.123 D.1.618
【分析】根据黄金分割点的定义,当AC是较长线段时,AC=AB,代入数据即可得出AC的长度.
【解答】解:∵线段AB=2,C是AB的黄金分割点,且AC>BC时,
∴AC=AB=×2=﹣1≈1.236,
故选:B.
6.(4分)如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP B.△APD∽△PGD C.△APG∽△BFP D.△PCF∽△BCP
【分析】由相似三角形的判定依次判断可求解.
【解答】解:∵∠CPD=∠A=∠B,且∠APD=∠B+∠PFB=∠APC+∠CPD,
∴∠APC=∠BFP,且∠A=∠B,
∴△APG∽△BFP,故选项C不合题意,
∵∠A=∠CPD,∠D=∠D,
∴△APD∽△PGD,故选项B不合题意,
∵∠B=∠CPD,∠C=∠C,
∴△PCF∽△BCP,故选项D不合题意,
由条件无法证明△CGE∽△CBP,
故选项A符合题意,
故选:A.
7.(4分)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:①该抛物线的开口向下;②该抛物线的顶点坐标为(1,5);③当x>2时,y随x的增大而减少;④3是方程ax2+bx+c=x的一个根.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
【分析】根据表格数据确定抛物线的对称轴和开口方向,进而求解.
【解答】解:①由表格数据可知,x=0和x=3的函数值都是3,
∵二次函数的对称轴为直线x=(0+3)=1.5,
从表格看,对称轴右侧,y随x的增大而减小,故抛物线开口向下,
故①正确,符合题意;
②抛物线的对称轴为直线x=1.5,
故②错误,不符合题意;
③由①知,x>1.5时,y随x的增大而减小,
故当x>2时,y随x的增大而减小,正确,符合题意;
④方程ax2+(b﹣1)x+c=0可化为方程ax2+bx+c=x,
由表格数据可知,x=3时,y=3,则3是方程ax2+bx+c=x的一个根,从而也是方程ax2+(b﹣1)x+c=0的一个根,
故本选项正确,符合题意;
故选:B.
8.(4分)如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,点C距灯柱AB的水平距离为1.6米,点C距水平地面的距离为2.5米,灯罩D距灯柱AB的水平距离为3.2米,灯柱AB=1.5米,则灯罩D到水平地面的距离为( )
A.1.5米 B.1米 C.1.2米 D.1.4米
【分析】根据题意和题目中的数据,可以得到点B和点D关于点C所在的直线对称,点C为抛物线的顶点,然后根据二次函数图象具有对称性,即可得到点D到水平地面的距离等于点B到水平地面的距离,从而可以解答本题.
【解答】解:由题意可得,
点C为抛物线的最高点,即抛物线的顶点,
∵点C距灯柱AB的水平距离为1.6米,灯罩D距灯柱AB的水平距离为3.2米,
∴点B和点D关于点C所在的直线对称,
∵灯柱AB=1.5米,
∴灯罩D到水平地面的距离为1.5米,
故选:A.
9.(4分)矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A. B.
C. D.
【分析】重点考查学生的阅读理解能力、分析研究能力.在解答时要注意先总结出函数的解析式,由解析式结合其取值范围判断,不要只靠感觉.
【解答】解:此题在读懂题意的基础上,分两种情况讨论:
当x≤4时,y=6×8﹣(x 2x)=﹣2x2+48,此时函数的图象为抛物线的一部分,它的最上点抛物线的顶点(0,48),最下点为(4,16);
当4<x≤6时,点E停留在B点处,故y=48﹣8x=﹣8x+48,此时函数的图象为直线y=﹣8x+48的一部分,它的最上点可以为(4,16),它的最下点为(6,0).
结合四个选项的图象知选A项.
故选:A.
10.(4分)如图,点P是等腰△ABC的腰AB上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
【分析】根据相似三角形的判定,过点P分别BC,AC的平行线即可得到与原三角形相似的三角形,过点P作以点P为顶点的角与∠A相等的角也可以得到原三角形相似的三角形.
【解答】解:∵BA=BC,
∴∠A=∠C,
①作PE∥BC,可得△APE∽△ABC.
②作PF∥AC,可得△BPF∽△BAC.
③作∠APG=∠A,可得∠AGP∽△ABC,
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)对于二次函数y=x2﹣4x+3,图象的对称轴为 直线x=2 ,当自变量x满足a≤x≤3时,函数值y的取值范围为﹣1≤y≤0,则a的取值范围为 1≤a≤2 .
【分析】函数的顶点D坐标为:(2,﹣1),则点A、B的坐标分别为:(1,0)、(3,0),从图象可以看出:y的取值范围为﹣1≤y≤0时,1<a≤2;即可求解.
【解答】解:∵二次函数y=x2﹣4x+3=(x﹣2)2﹣1,
∴函数的对称轴为:直线x=2,
函数图象如下,函数的对称轴为:直线x=2,顶点D坐标为:(2,﹣1),
则点A、B的坐标分别为:(1,0)、(3,0),
从图象可以看出:y的取值范围为﹣1≤y≤0时,
1≤a≤2;
故答案为:直线x=2,1≤a≤2.
12.(5分)已知反比例函数,若x≥2,则y的取值范围为 0<y≤3 .
【分析】求得x=2时的函数值,然后根据反比例函数的性质即可得到y的取值范围.
【解答】解:∵反比例函数中,k=6>0,
∴图象在第一、三象限,且在每个象限y随x的增大而减小,
∵当x=2时,y=3,
∴当x≥2时,0<y≤3.
故答案:0<y≤3.
13.(5分)如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
【分析】过E点作EH∥AC交BD于H,如图,根据平行线分线段成比例定理,由EH∥CD得到=,由于AD=CD,则=,然后利用EH∥AD,根据平行线分线段成比例定理得的值.
【解答】解:过E点作EH∥AC交BD于H,如图,
∵EH∥CD,
∴=,
∵BE=3EC,
∴==,
∵D是AC的中点,
∴AD=CD,
∴=,
∵EH∥AD,
∴==.
故答案为.
14.(5分)如果一个正比例函数的图象与反比例函数y=的图象交于A(x1,y1),B(x2,y2)两点,那么(x2﹣x1)(y2﹣y1)的值为 16 .
【分析】正比例函数与反比例函数y=的两交点坐标关于原点对称,依此可得x1=﹣x2,y1=﹣y2,将(x2﹣x1)(y2﹣y1)展开,依此关系即可求解.
【解答】解:∵正比例函数的图象与反比例函数y=的图象交于A(x1,y1),B(x2,y2)两点,关于原点对称,依此可得x1=﹣x2,y1=﹣y2,
∴(x2﹣x1)(y2﹣y1)
=x2y2﹣x2y1﹣x1y2+x1y1
=x2y2+x2y2+x1y1+x1y1
=4×4
=16.
故答案为:16.
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知:二次函数y=x2﹣4x+3a+2(a为常数).
(1)请写出该二次函数图象的对称轴;
(2)若这个二次函数的最小值是7,求a的值;
(3)直角坐标系中,若该二次函数的图象在x≤4的部分与一次函数y=2x﹣1的图象有两个交点,求a的取值范围.
【分析】(1)由x=﹣求得对称轴;
(2)将对称轴的x值代入函数解析式求得函数的最小值,然后求出a的值;
(3)将函数的交点转化为对应的一元二次方程的两根均小于或等于4求解.
【解答】解:(1)对称轴为直线x=﹣==2.
(2)当x=2时,y最小值=22﹣4×2+3a+2=4﹣8+3a+2=3a﹣2,
∵最小值是7,
∴3a﹣2=7,
解得:a=3.
(3)∵该二次函数的图像在x≤4的部分与一次函数y=2x﹣1的图像有两个交点,
∴x2﹣4x+3a+2=2x﹣1在x≤4的范围内有两个不同的实数根,
化简得:x2﹣6x+3a+3=0,
Δ=36﹣4(3a+3)>0,
解得:a<2,
∵x2﹣6x+3a+3=0在x≤4的范围内有两个不同的实数根,
∴x=4时,y=16﹣24+3a+3≥0,
∴a≥,
∴≤a<2.
16.(8分)如图,在平面直角坐标系xOy中,直线y=﹣2x﹣2与双曲线交于M(a,2),N(1,b)两点.
(1)求k,a,b的值.
(2)若P是y轴上一点,且△MPN的面积是6,直接写出点P的坐标 (0,2)或(0,﹣6) .
【分析】(1)用待定系数法即可求解;
(2)S△MPN=S△PAM+S△PAN=6,求出PA=4,即可求解.
【解答】解:(1)把M(a,2)、N(1,b)代入y=﹣2x﹣2中得:﹣2a﹣2=2,b=﹣2﹣2=﹣4,
∴a=﹣2,b=﹣4,
即M(﹣2,2),N(1,﹣4),
把M(﹣2,2)代入中,得k=xy=﹣4,
∴k=﹣4,a=﹣2,b=﹣4;
(2)设直线y=﹣2x﹣2与y轴交于点A,
令x=0,即y=﹣2,故A(0,﹣2),
S△MPN=S△PAM+S△PAN=PA×(xN﹣xM)=×PA×(1+2)=6,
∴PA=4
∴P(0,2)或(0,﹣6),
故答案为(0,2)或(0,﹣6).
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)已知xyz≠0且,求k的值.
【分析】分①当x+y+z≠0时,利用等比性质解答,②当x+y+z=0时,用一个字母表示出另两个字母的和,然后求解即可.
【解答】解:∵xyz≠0,
∴x、y、z均不为0,
①当x+y+z≠0时,∵===k,
∴k==2,
②当x+y+z=0时,x+y=﹣z,z+x=﹣y,y+z=﹣x,
所以,k=﹣1,
综上所述,k=2或﹣1.
18.(8分)如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
【分析】在△ABC中,根据平行线分线段成比例求出EG,在△BAD中,根据平行线分线段成比例求出EF,即可求出FG=EG﹣EF.
【解答】解:∵△ABC中,EG∥BC,
∴△AEG∽△ABC,
∴,
∵BC=10,AE=9,AB=12,
∴=,
∴EG=,
∵△BAD中,EF∥AD,
∴=,
∵AD=5,AE=9,AB=12,
∴=,
∴EF=.
∴FG=EG﹣EF=﹣=.
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)新冠肺炎疫情期间,某药店进了一批口罩,每包进价10元,每包销售价定为25元时,每天销售1000包.经一段时间调查,发现每包销售单价每上涨1元,每天就少卖40包.其销售单价不低于进价,销售利润率不高于180%.设每包销售价为x元(x为正整数).
(1)请直接写出x的取值范围.
(2)设每天的总利润为w元,当每包销售价定为多少元时,该药店每天的利润最大?最大利润是多少元?
【分析】(1)根据销售单价不低于进价,销售利润率不高于180%求解即可得到答案;
(2)求出w关于的关系式,利用二次函数的性质求解即可.
【解答】解:(1)∵销售单价不低于进价,销售利润率不高于180%,
∴,
解得:10≤x≤28,
∴x的取值范围10≤x≤28;
(2)由题意,得w=(x﹣10)[1000﹣40(x﹣25)],
即w=﹣40x2+2400x﹣20000=﹣40(x﹣30)2+16000,
∵a=﹣40<0,
∴抛物线开口向下,w有最大值,
∵10≤x≤28,当x<30时,w随x的增大而增大,
∴当x=28时,w有最大值,最大值是﹣40×(28﹣30)2+16000=15840,
答:销售单价定为每包28元时,每天的利润最大,最大利润是15840元.
20.(10分)如图,点M是AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)求证:△AMF∽△BGM;
(2)请你再写出两对相似三角形.
【分析】(1)根据两角对应相等的两个三角形相似证明即可.
(2)根据相似三角形的判定解决问题即可.
【解答】(1)证明:∵∠DME=∠A=∠B=α,
∴∠AMF+∠BMG=180°﹣α,
∵∠A+∠AMF+∠AFM=180°,
∴∠AMF+∠AFM=180°﹣α,
∴∠AFM=∠BMG,
∴△AMF∽△BGM;
(2)解:∵∠D=∠D,∠DMG=∠DBM.
∴△DMG∽△DBM,
同法可证:△EMF∽△EAM.
六、(本题满分12分)
21.(12分)已知抛物线y=ax2+2ax+3a2﹣4(a≠0).
(1)该抛物线的对称轴为 x=﹣1 ;
(2)若该抛物线的顶点在x轴上,求抛物线的解析式;
(3)设点M(m,y1),N(2,y2)在该抛物线上,若y1>y2,求m的取值范围.
【分析】(1)根据题意可得抛物线的对称轴;
(2)抛物线的顶点在x轴上,可得顶点坐标为(﹣1,0),进而可得a的值;
(3)根据点N(2,y2)关于直线x=﹣1的对称点为N′(﹣4,y2),进而可得m的取值范围.
【解答】解:(1)∵抛物线y=ax2+2ax+3a2﹣4.
∴对称轴为直线x==﹣1,
故答案为:直线x=﹣1;
(2)y=ax2+2ax+3a2﹣4
=a(x+1)2+3a2﹣a﹣4,
∵抛物线顶点在x轴上,
即当x=﹣1时,y=0,
∴3a2﹣a﹣4=0,
解得.
∴抛物线解析式为y=﹣x2﹣2x﹣1或.
(3)∵抛物线的对称轴为直线x=﹣1,
∴N(2,y2)关于直线x=﹣1的对称点为N’(﹣4,y2).
(ⅰ)当a>0时,若y1>y2,则m<﹣4或m>2;
(ⅱ)当a<0时,若y1>y2,则﹣4<m<2.
七、(本题满分12分)
22.(12分)如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+6﹣>0的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
【分析】(1)求出点A的坐标,利用待定系数法即可解决问题;
(2)结合函数图象找到直线在双曲线上方对应的x的取值范围;
(3)构建二次函数,利用二次函数的性质即可解决问题.
【解答】解:(1)∵直线y=2x+6经过点A(1,m),
∴m=2×1+6=8,
∴A(1,8),
∵反比例函数经过点A(1,8),
∴k=8,
∴反比例函数的解析式为y=.
(2)不等式2x+6﹣>0的解集为x>1.
(3)由题意,点M,N的坐标为M(,n),N(,n),
∵0<n<6,
∴<0,
∴﹣>0
∴S△BMN=|MN|×|yM|=×(﹣)×n=﹣(n﹣3)2+,
∴n=3时,△BMN的面积最大,最大值为.
八、(本题满分14分)
23.(14分)某服装批发市场销售一种衬衫,衬衫每件进货价为50元.规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求出y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价?
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的50%,设销售这种衬衫每月的总利润为w(元),求w与x之间的函数关系式,x为多少时,w有最大值,最大利润是多少?
【分析】(1)根据题意和表格中的数据可以得到y与x之间的函数表达式;
(2)根据题意,可以得到相应的方程,从而可以得到如何给这种衬衫定价,可以给客户最大优惠;
(3)根据题意,可以得到w与x之间的函数关系式,再根据二次函数的性质,即可得到售价定为多少元可获得最大利润,最大利润是多少.
【解答】解:(1)设y与x之间的函数关系式为y=kx+b,
,
解得,,
即y与x之间的函数表达式是y=﹣20x+2600;
(2)(x﹣50)(﹣20x+2600)=24000,
解得,x1=70,x2=110,
∵尽量给客户优惠,
∴这种衬衫定价为70元;
(3)由题意可得,
w=(x﹣50)(﹣20x+2600),
=﹣20x2+3600x﹣130000,
w=﹣20(x﹣90)2+32000,
∵该衬衫的每件利润不允许高于进货价的50%,每件售价不低于进货价,
∴,
解得,50≤x≤75,
∵a=﹣20<0,抛物线开口向下,
∴当x=75时,w取得最大值,此时w=27500,
答:售价定为75元时,可获得最大利润,最大利润是27500元.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)抛物线y=﹣(x+1)2﹣3的顶点坐标是( )
A.(﹣1,﹣3) B.(﹣1,3) C.(1,﹣3) D.(1,3)
2.(4分)已知二次函数的图象与x轴有两个交点,且顶点坐标为(﹣2,1).若函数图象经过(1,y1),(﹣1,y2),(﹣4,y3)三点,则( )
A.y1<y3<y2 B.y2<y1<y3 C.y1<y2<y3 D.y2<y3<y1
3.(4分)关于二次函数y=x2+2x﹣8,下列说法正确的是( )
A.图象的对称轴在y轴的右侧
B.图象与y轴的交点坐标为(0,8)
C.图象与x轴的交点坐标为(﹣2,0)和(4,0)
D.y的最小值为﹣9
4.(4分)已知二次函数y=﹣(x+a)2﹣b的图象如图所示,则反比例函数与一次函数y=ax+b的图象可能是( )
A. B.
C. D.
5.(4分)如图所示,已知点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC的长约为( )
A.1.543 B.1.236 C.1.123 D.1.618
6.(4分)如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP B.△APD∽△PGD C.△APG∽△BFP D.△PCF∽△BCP
7.(4分)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:①该抛物线的开口向下;②该抛物线的顶点坐标为(1,5);③当x>2时,y随x的增大而减少;④3是方程ax2+bx+c=x的一个根.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
8.(4分)如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,点C距灯柱AB的水平距离为1.6米,点C距水平地面的距离为2.5米,灯罩D距灯柱AB的水平距离为3.2米,灯柱AB=1.5米,则灯罩D到水平地面的距离为( )
A.1.5米 B.1米 C.1.2米 D.1.4米
9.(4分)矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A. B.
C. D.
10.(4分)如图,点P是等腰△ABC的腰AB上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)对于二次函数y=x2﹣4x+3,图象的对称轴为 ,当自变量x满足a≤x≤3时,函数值y的取值范围为﹣1≤y≤0,则a的取值范围为 .
12.(5分)已知反比例函数,若x≥2,则y的取值范围为 .
13.(5分)如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
14.(5分)如果一个正比例函数的图象与反比例函数y=的图象交于A(x1,y1),B(x2,y2)两点,那么(x2﹣x1)(y2﹣y1)的值为 .
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知:二次函数y=x2﹣4x+3a+2(a为常数).
(1)请写出该二次函数图象的对称轴;
(2)若这个二次函数的最小值是7,求a的值;
(3)直角坐标系中,若该二次函数的图象在x≤4的部分与一次函数y=2x﹣1的图象有两个交点,求a的取值范围.
16.(8分)如图,在平面直角坐标系xOy中,直线y=﹣2x﹣2与双曲线交于M(a,2),N(1,b)两点.
(1)求k,a,b的值.
(2)若P是y轴上一点,且△MPN的面积是6,直接写出点P的坐标 .
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)已知xyz≠0且,求k的值.
18.(8分)如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)新冠肺炎疫情期间,某药店进了一批口罩,每包进价10元,每包销售价定为25元时,每天销售1000包.经一段时间调查,发现每包销售单价每上涨1元,每天就少卖40包.其销售单价不低于进价,销售利润率不高于180%.设每包销售价为x元(x为正整数).
(1)请直接写出x的取值范围.
(2)设每天的总利润为w元,当每包销售价定为多少元时,该药店每天的利润最大?最大利润是多少元?
20.(10分)如图,点M是AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)求证:△AMF∽△BGM;
(2)请你再写出两对相似三角形.
六、(本题满分12分)
21.(12分)已知抛物线y=ax2+2ax+3a2﹣4(a≠0).
(1)该抛物线的对称轴为 ;
(2)若该抛物线的顶点在x轴上,求抛物线的解析式;
(3)设点M(m,y1),N(2,y2)在该抛物线上,若y1>y2,求m的取值范围.
七、(本题满分12分)
22.(12分)如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+6﹣>0的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
八、(本题满分14分)
23.(14分)某服装批发市场销售一种衬衫,衬衫每件进货价为50元.规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求出y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价?
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的50%,设销售这种衬衫每月的总利润为w(元),求w与x之间的函数关系式,x为多少时,w有最大值,最大利润是多少?
2021-2022学年安徽省合肥三十中九年级(上)期中数学模拟练习试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)抛物线y=﹣(x+1)2﹣3的顶点坐标是( )
A.(﹣1,﹣3) B.(﹣1,3) C.(1,﹣3) D.(1,3)
【分析】直接利用顶点式的特点可知顶点坐标.
【解答】解:抛物线y=﹣(x+1)2﹣3的顶点坐标是(﹣1,﹣3)
故选:A.
2.(4分)已知二次函数的图象与x轴有两个交点,且顶点坐标为(﹣2,1).若函数图象经过(1,y1),(﹣1,y2),(﹣4,y3)三点,则( )
A.y1<y3<y2 B.y2<y1<y3 C.y1<y2<y3 D.y2<y3<y1
【分析】先判断出二次函数的开口方向,再求出点(1,y1),(﹣1,y2),(﹣4,y3)到对称轴的距离,然后根据二次函数增减性判断即可.
【解答】解:∵图象与x轴有两个交点,且顶点坐标为(﹣2,1).
∴对称轴为直线x=﹣2,开口向下,
∵(1,y1),(﹣1,y2),(﹣4,y3)与对称轴的距离y2最近,y3最远,
∴y1<y3<y2.
故选:A.
3.(4分)关于二次函数y=x2+2x﹣8,下列说法正确的是( )
A.图象的对称轴在y轴的右侧
B.图象与y轴的交点坐标为(0,8)
C.图象与x轴的交点坐标为(﹣2,0)和(4,0)
D.y的最小值为﹣9
【分析】根据题目中的函数解析式和二次函数的性质,可以判断各个选项中的结论是否正确,从而可以解答本题.
【解答】解:∵二次函数y=x2+2x﹣8=(x+1)2﹣9=(x+4)(x﹣2),
∴该函数的对称轴是直线x=﹣1,在y轴的左侧,故选项A错误;
当x=0时,y=﹣8,即该函数与y轴交于点(0,﹣8),故选项B错误;
当y=0时,x=2或x=﹣4,即图象与x轴的交点坐标为(2,0)和(﹣4,0),故选项C错误;
当x=﹣1时,该函数取得最小值y=﹣9,故选项D正确;
故选:D.
4.(4分)已知二次函数y=﹣(x+a)2﹣b的图象如图所示,则反比例函数与一次函数y=ax+b的图象可能是( )
A. B.
C. D.
【分析】观察二次函数图象,找出a<0,b>0,再结合反比例(一次)函数图象与系数的关系,即可得出结论.
【解答】解:观察二次函数图象,发现:抛物线的顶点坐标在第四象限,开口向下,对称在y轴右侧,
∴﹣a>0,﹣b<0,
∴a<0,b>0.
∵反比例函数中ab<0,
∴反比例函数图象在第二、四象限;
∵一次函数y=ax+b,a<0,b>0,
∴一次函数y=ax+b的图象过第一、二、四象限.
故选:D.
5.(4分)如图所示,已知点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC的长约为( )
A.1.543 B.1.236 C.1.123 D.1.618
【分析】根据黄金分割点的定义,当AC是较长线段时,AC=AB,代入数据即可得出AC的长度.
【解答】解:∵线段AB=2,C是AB的黄金分割点,且AC>BC时,
∴AC=AB=×2=﹣1≈1.236,
故选:B.
6.(4分)如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP B.△APD∽△PGD C.△APG∽△BFP D.△PCF∽△BCP
【分析】由相似三角形的判定依次判断可求解.
【解答】解:∵∠CPD=∠A=∠B,且∠APD=∠B+∠PFB=∠APC+∠CPD,
∴∠APC=∠BFP,且∠A=∠B,
∴△APG∽△BFP,故选项C不合题意,
∵∠A=∠CPD,∠D=∠D,
∴△APD∽△PGD,故选项B不合题意,
∵∠B=∠CPD,∠C=∠C,
∴△PCF∽△BCP,故选项D不合题意,
由条件无法证明△CGE∽△CBP,
故选项A符合题意,
故选:A.
7.(4分)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:①该抛物线的开口向下;②该抛物线的顶点坐标为(1,5);③当x>2时,y随x的增大而减少;④3是方程ax2+bx+c=x的一个根.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
【分析】根据表格数据确定抛物线的对称轴和开口方向,进而求解.
【解答】解:①由表格数据可知,x=0和x=3的函数值都是3,
∵二次函数的对称轴为直线x=(0+3)=1.5,
从表格看,对称轴右侧,y随x的增大而减小,故抛物线开口向下,
故①正确,符合题意;
②抛物线的对称轴为直线x=1.5,
故②错误,不符合题意;
③由①知,x>1.5时,y随x的增大而减小,
故当x>2时,y随x的增大而减小,正确,符合题意;
④方程ax2+(b﹣1)x+c=0可化为方程ax2+bx+c=x,
由表格数据可知,x=3时,y=3,则3是方程ax2+bx+c=x的一个根,从而也是方程ax2+(b﹣1)x+c=0的一个根,
故本选项正确,符合题意;
故选:B.
8.(4分)如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,点C距灯柱AB的水平距离为1.6米,点C距水平地面的距离为2.5米,灯罩D距灯柱AB的水平距离为3.2米,灯柱AB=1.5米,则灯罩D到水平地面的距离为( )
A.1.5米 B.1米 C.1.2米 D.1.4米
【分析】根据题意和题目中的数据,可以得到点B和点D关于点C所在的直线对称,点C为抛物线的顶点,然后根据二次函数图象具有对称性,即可得到点D到水平地面的距离等于点B到水平地面的距离,从而可以解答本题.
【解答】解:由题意可得,
点C为抛物线的最高点,即抛物线的顶点,
∵点C距灯柱AB的水平距离为1.6米,灯罩D距灯柱AB的水平距离为3.2米,
∴点B和点D关于点C所在的直线对称,
∵灯柱AB=1.5米,
∴灯罩D到水平地面的距离为1.5米,
故选:A.
9.(4分)矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A. B.
C. D.
【分析】重点考查学生的阅读理解能力、分析研究能力.在解答时要注意先总结出函数的解析式,由解析式结合其取值范围判断,不要只靠感觉.
【解答】解:此题在读懂题意的基础上,分两种情况讨论:
当x≤4时,y=6×8﹣(x 2x)=﹣2x2+48,此时函数的图象为抛物线的一部分,它的最上点抛物线的顶点(0,48),最下点为(4,16);
当4<x≤6时,点E停留在B点处,故y=48﹣8x=﹣8x+48,此时函数的图象为直线y=﹣8x+48的一部分,它的最上点可以为(4,16),它的最下点为(6,0).
结合四个选项的图象知选A项.
故选:A.
10.(4分)如图,点P是等腰△ABC的腰AB上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
【分析】根据相似三角形的判定,过点P分别BC,AC的平行线即可得到与原三角形相似的三角形,过点P作以点P为顶点的角与∠A相等的角也可以得到原三角形相似的三角形.
【解答】解:∵BA=BC,
∴∠A=∠C,
①作PE∥BC,可得△APE∽△ABC.
②作PF∥AC,可得△BPF∽△BAC.
③作∠APG=∠A,可得∠AGP∽△ABC,
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)对于二次函数y=x2﹣4x+3,图象的对称轴为 直线x=2 ,当自变量x满足a≤x≤3时,函数值y的取值范围为﹣1≤y≤0,则a的取值范围为 1≤a≤2 .
【分析】函数的顶点D坐标为:(2,﹣1),则点A、B的坐标分别为:(1,0)、(3,0),从图象可以看出:y的取值范围为﹣1≤y≤0时,1<a≤2;即可求解.
【解答】解:∵二次函数y=x2﹣4x+3=(x﹣2)2﹣1,
∴函数的对称轴为:直线x=2,
函数图象如下,函数的对称轴为:直线x=2,顶点D坐标为:(2,﹣1),
则点A、B的坐标分别为:(1,0)、(3,0),
从图象可以看出:y的取值范围为﹣1≤y≤0时,
1≤a≤2;
故答案为:直线x=2,1≤a≤2.
12.(5分)已知反比例函数,若x≥2,则y的取值范围为 0<y≤3 .
【分析】求得x=2时的函数值,然后根据反比例函数的性质即可得到y的取值范围.
【解答】解:∵反比例函数中,k=6>0,
∴图象在第一、三象限,且在每个象限y随x的增大而减小,
∵当x=2时,y=3,
∴当x≥2时,0<y≤3.
故答案:0<y≤3.
13.(5分)如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
【分析】过E点作EH∥AC交BD于H,如图,根据平行线分线段成比例定理,由EH∥CD得到=,由于AD=CD,则=,然后利用EH∥AD,根据平行线分线段成比例定理得的值.
【解答】解:过E点作EH∥AC交BD于H,如图,
∵EH∥CD,
∴=,
∵BE=3EC,
∴==,
∵D是AC的中点,
∴AD=CD,
∴=,
∵EH∥AD,
∴==.
故答案为.
14.(5分)如果一个正比例函数的图象与反比例函数y=的图象交于A(x1,y1),B(x2,y2)两点,那么(x2﹣x1)(y2﹣y1)的值为 16 .
【分析】正比例函数与反比例函数y=的两交点坐标关于原点对称,依此可得x1=﹣x2,y1=﹣y2,将(x2﹣x1)(y2﹣y1)展开,依此关系即可求解.
【解答】解:∵正比例函数的图象与反比例函数y=的图象交于A(x1,y1),B(x2,y2)两点,关于原点对称,依此可得x1=﹣x2,y1=﹣y2,
∴(x2﹣x1)(y2﹣y1)
=x2y2﹣x2y1﹣x1y2+x1y1
=x2y2+x2y2+x1y1+x1y1
=4×4
=16.
故答案为:16.
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知:二次函数y=x2﹣4x+3a+2(a为常数).
(1)请写出该二次函数图象的对称轴;
(2)若这个二次函数的最小值是7,求a的值;
(3)直角坐标系中,若该二次函数的图象在x≤4的部分与一次函数y=2x﹣1的图象有两个交点,求a的取值范围.
【分析】(1)由x=﹣求得对称轴;
(2)将对称轴的x值代入函数解析式求得函数的最小值,然后求出a的值;
(3)将函数的交点转化为对应的一元二次方程的两根均小于或等于4求解.
【解答】解:(1)对称轴为直线x=﹣==2.
(2)当x=2时,y最小值=22﹣4×2+3a+2=4﹣8+3a+2=3a﹣2,
∵最小值是7,
∴3a﹣2=7,
解得:a=3.
(3)∵该二次函数的图像在x≤4的部分与一次函数y=2x﹣1的图像有两个交点,
∴x2﹣4x+3a+2=2x﹣1在x≤4的范围内有两个不同的实数根,
化简得:x2﹣6x+3a+3=0,
Δ=36﹣4(3a+3)>0,
解得:a<2,
∵x2﹣6x+3a+3=0在x≤4的范围内有两个不同的实数根,
∴x=4时,y=16﹣24+3a+3≥0,
∴a≥,
∴≤a<2.
16.(8分)如图,在平面直角坐标系xOy中,直线y=﹣2x﹣2与双曲线交于M(a,2),N(1,b)两点.
(1)求k,a,b的值.
(2)若P是y轴上一点,且△MPN的面积是6,直接写出点P的坐标 (0,2)或(0,﹣6) .
【分析】(1)用待定系数法即可求解;
(2)S△MPN=S△PAM+S△PAN=6,求出PA=4,即可求解.
【解答】解:(1)把M(a,2)、N(1,b)代入y=﹣2x﹣2中得:﹣2a﹣2=2,b=﹣2﹣2=﹣4,
∴a=﹣2,b=﹣4,
即M(﹣2,2),N(1,﹣4),
把M(﹣2,2)代入中,得k=xy=﹣4,
∴k=﹣4,a=﹣2,b=﹣4;
(2)设直线y=﹣2x﹣2与y轴交于点A,
令x=0,即y=﹣2,故A(0,﹣2),
S△MPN=S△PAM+S△PAN=PA×(xN﹣xM)=×PA×(1+2)=6,
∴PA=4
∴P(0,2)或(0,﹣6),
故答案为(0,2)或(0,﹣6).
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)已知xyz≠0且,求k的值.
【分析】分①当x+y+z≠0时,利用等比性质解答,②当x+y+z=0时,用一个字母表示出另两个字母的和,然后求解即可.
【解答】解:∵xyz≠0,
∴x、y、z均不为0,
①当x+y+z≠0时,∵===k,
∴k==2,
②当x+y+z=0时,x+y=﹣z,z+x=﹣y,y+z=﹣x,
所以,k=﹣1,
综上所述,k=2或﹣1.
18.(8分)如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
【分析】在△ABC中,根据平行线分线段成比例求出EG,在△BAD中,根据平行线分线段成比例求出EF,即可求出FG=EG﹣EF.
【解答】解:∵△ABC中,EG∥BC,
∴△AEG∽△ABC,
∴,
∵BC=10,AE=9,AB=12,
∴=,
∴EG=,
∵△BAD中,EF∥AD,
∴=,
∵AD=5,AE=9,AB=12,
∴=,
∴EF=.
∴FG=EG﹣EF=﹣=.
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)新冠肺炎疫情期间,某药店进了一批口罩,每包进价10元,每包销售价定为25元时,每天销售1000包.经一段时间调查,发现每包销售单价每上涨1元,每天就少卖40包.其销售单价不低于进价,销售利润率不高于180%.设每包销售价为x元(x为正整数).
(1)请直接写出x的取值范围.
(2)设每天的总利润为w元,当每包销售价定为多少元时,该药店每天的利润最大?最大利润是多少元?
【分析】(1)根据销售单价不低于进价,销售利润率不高于180%求解即可得到答案;
(2)求出w关于的关系式,利用二次函数的性质求解即可.
【解答】解:(1)∵销售单价不低于进价,销售利润率不高于180%,
∴,
解得:10≤x≤28,
∴x的取值范围10≤x≤28;
(2)由题意,得w=(x﹣10)[1000﹣40(x﹣25)],
即w=﹣40x2+2400x﹣20000=﹣40(x﹣30)2+16000,
∵a=﹣40<0,
∴抛物线开口向下,w有最大值,
∵10≤x≤28,当x<30时,w随x的增大而增大,
∴当x=28时,w有最大值,最大值是﹣40×(28﹣30)2+16000=15840,
答:销售单价定为每包28元时,每天的利润最大,最大利润是15840元.
20.(10分)如图,点M是AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)求证:△AMF∽△BGM;
(2)请你再写出两对相似三角形.
【分析】(1)根据两角对应相等的两个三角形相似证明即可.
(2)根据相似三角形的判定解决问题即可.
【解答】(1)证明:∵∠DME=∠A=∠B=α,
∴∠AMF+∠BMG=180°﹣α,
∵∠A+∠AMF+∠AFM=180°,
∴∠AMF+∠AFM=180°﹣α,
∴∠AFM=∠BMG,
∴△AMF∽△BGM;
(2)解:∵∠D=∠D,∠DMG=∠DBM.
∴△DMG∽△DBM,
同法可证:△EMF∽△EAM.
六、(本题满分12分)
21.(12分)已知抛物线y=ax2+2ax+3a2﹣4(a≠0).
(1)该抛物线的对称轴为 x=﹣1 ;
(2)若该抛物线的顶点在x轴上,求抛物线的解析式;
(3)设点M(m,y1),N(2,y2)在该抛物线上,若y1>y2,求m的取值范围.
【分析】(1)根据题意可得抛物线的对称轴;
(2)抛物线的顶点在x轴上,可得顶点坐标为(﹣1,0),进而可得a的值;
(3)根据点N(2,y2)关于直线x=﹣1的对称点为N′(﹣4,y2),进而可得m的取值范围.
【解答】解:(1)∵抛物线y=ax2+2ax+3a2﹣4.
∴对称轴为直线x==﹣1,
故答案为:直线x=﹣1;
(2)y=ax2+2ax+3a2﹣4
=a(x+1)2+3a2﹣a﹣4,
∵抛物线顶点在x轴上,
即当x=﹣1时,y=0,
∴3a2﹣a﹣4=0,
解得.
∴抛物线解析式为y=﹣x2﹣2x﹣1或.
(3)∵抛物线的对称轴为直线x=﹣1,
∴N(2,y2)关于直线x=﹣1的对称点为N’(﹣4,y2).
(ⅰ)当a>0时,若y1>y2,则m<﹣4或m>2;
(ⅱ)当a<0时,若y1>y2,则﹣4<m<2.
七、(本题满分12分)
22.(12分)如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+6﹣>0的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
【分析】(1)求出点A的坐标,利用待定系数法即可解决问题;
(2)结合函数图象找到直线在双曲线上方对应的x的取值范围;
(3)构建二次函数,利用二次函数的性质即可解决问题.
【解答】解:(1)∵直线y=2x+6经过点A(1,m),
∴m=2×1+6=8,
∴A(1,8),
∵反比例函数经过点A(1,8),
∴k=8,
∴反比例函数的解析式为y=.
(2)不等式2x+6﹣>0的解集为x>1.
(3)由题意,点M,N的坐标为M(,n),N(,n),
∵0<n<6,
∴<0,
∴﹣>0
∴S△BMN=|MN|×|yM|=×(﹣)×n=﹣(n﹣3)2+,
∴n=3时,△BMN的面积最大,最大值为.
八、(本题满分14分)
23.(14分)某服装批发市场销售一种衬衫,衬衫每件进货价为50元.规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求出y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价?
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的50%,设销售这种衬衫每月的总利润为w(元),求w与x之间的函数关系式,x为多少时,w有最大值,最大利润是多少?
【分析】(1)根据题意和表格中的数据可以得到y与x之间的函数表达式;
(2)根据题意,可以得到相应的方程,从而可以得到如何给这种衬衫定价,可以给客户最大优惠;
(3)根据题意,可以得到w与x之间的函数关系式,再根据二次函数的性质,即可得到售价定为多少元可获得最大利润,最大利润是多少.
【解答】解:(1)设y与x之间的函数关系式为y=kx+b,
,
解得,,
即y与x之间的函数表达式是y=﹣20x+2600;
(2)(x﹣50)(﹣20x+2600)=24000,
解得,x1=70,x2=110,
∵尽量给客户优惠,
∴这种衬衫定价为70元;
(3)由题意可得,
w=(x﹣50)(﹣20x+2600),
=﹣20x2+3600x﹣130000,
w=﹣20(x﹣90)2+32000,
∵该衬衫的每件利润不允许高于进货价的50%,每件售价不低于进货价,
∴,
解得,50≤x≤75,
∵a=﹣20<0,抛物线开口向下,
∴当x=75时,w取得最大值,此时w=27500,
答:售价定为75元时,可获得最大利润,最大利润是27500元.
同课章节目录
