2021-2022学年上海市浦东新区交中初级中学八年级(上)第一次月考数学试卷(10月份)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年上海市浦东新区交中初级中学八年级(上)第一次月考数学试卷(10月份)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 09:48:52 | ||
图片预览




文档简介
2021-2022学年上海市浦东新区交中初级中学八年级第一学期第一次月考数学试卷(10月份)
一、选择题(本大题共6小题,共24分)
1.用配方法解一元二次方程x2﹣6x﹣7=0,则方程变形为( )
A.(x﹣6)2=43 B.(x+6)2=43 C.(x﹣3)2=16 D.(x+3)2=16
2.已知Rt△ABC中,∠C=90°,且BC=AB,则∠A等于( )
A.30° B.45° C.60° D.不能确定
3.下列各式中,计算错误的是( )
A. B.
C.(a≥0) D.
4.下列命题中真命题是( )
A.如果两个直角三角形的两条边相等,那么这两个直角三角形全等
B.如果两个直角三角形的一条边和一个锐角对应相等,那么这两个直角三角形全等
C.如果两个直角三角形的两个角对应相等,那么这两个直角三角形全等
D.如果两个直角三角形的一条直角边和斜边对应相等,那么这两个直角三角形全等
5.如图,A,C是函数的图象上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则S1和S2的大小关系是( )
A.S1>S2 B.S1<S2
C.S1=S2 D.由A,C两点的位置确定
6.如图1,在平行四边形ABCD中,AD=5cm,CD=3cm,AC⊥CD,点P从点C出发,以1cm/s的速度沿C→D→A匀速运动,点M从点B出发,以相同的速度沿B→C匀速运动,其中一点停止时,另一点随之停止运动,图2是△PMC的面积S(cm2)随时间t(s)变化的函数图象,若a秒与b秒时△PMC的面积均为cm2,则b﹣a的值为( )
A. B. C.3 D.
二、填空题(本大题共12小题,共48分)
7.已知函数y=,则自变量x的取值范围是 .
8.已知函数,则= .
9.方程x2=2x的根为 .
10.已知函数的图象经过点(2,5),则实数k= .
11.命题“同旁内角互补,两直线平行”中,题设是 ,结论是 ;此命题是 (填“真命题”或“假命题”)
12.已知关于x的方程(m﹣2)x2﹣2x+1=0有实数根,则实数m的取值范围是 .
13.已知实数a在数轴上的位置如图所示,化简= .
14.已知函数y=2x与的图象的一个交点坐标是(1,2),则它们的图象的另一个交点的坐标是 .
15.如图,已知Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,现将△ABC进行折叠,使顶点A、B重合,则折痕DE= cm.
16.已知直角三角形的两边长为x,y,且满足|x2﹣4|+=0,则第三边长为 .
17.如图,已知在△ABC中,AB=AC=6,∠BAC=30°,将△ABC沿AC翻折,使点B落在点D处,延长AD与BC的延长线相交于点E,则DE的长为 .
18.已知在△ABC中,∠C=90°,AC=3,BC=4,在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,若旋转后点C的对应点C′落直线AB上,那么AA′的长为 .
三、解答题(本大题共7小题,共78分)
19.已知,求代数式20x2+55xy+20y2的值.
20.若实数m,n满足|m﹣2|+=0,请用配方法解关于x的一元二次方程x2+mx+n=0.
21.如图,已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等.(尺规作图,不写作法,保留作图痕迹)
22.为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.
23.已知△ABC中,AD是∠BAC的平分线,且AD=AB,过点C作AD的垂线,交AD的延长线于点H.
(1)如图1,若∠BAC=60°.
①直接写出∠B和∠ACB的度数;
②若AB=2,求AC和AH的长;
(2)如图2,用等式表示线段AH与AB+AC之间的数量关系,并证明.
24.已知反比例函数y=的图象经过点A(﹣,1).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;
(3)已知点P(m,m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2n+9的值.
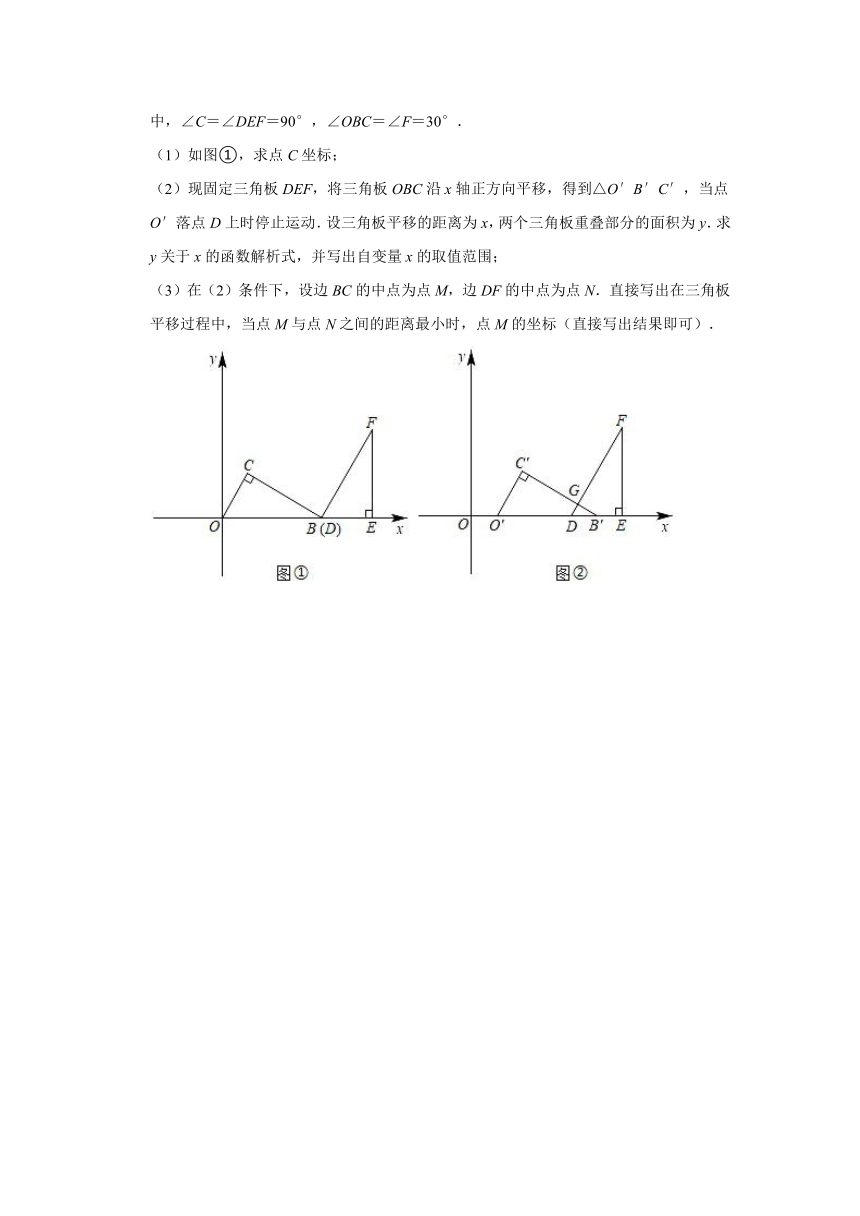
25.在平面直角坐标系中,两个形状、大小完全相同的三角板OBC,DEF,按如图所示的位置摆放,O为原点,点B(12,0),点B与点D重合,边OB与边DE都在x轴上.其中,∠C=∠DEF=90°,∠OBC=∠F=30°.
(1)如图①,求点C坐标;
(2)现固定三角板DEF,将三角板OBC沿x轴正方向平移,得到△O′B′C′,当点O′落点D上时停止运动.设三角板平移的距离为x,两个三角板重叠部分的面积为y.求y关于x的函数解析式,并写出自变量x的取值范围;
(3)在(2)条件下,设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,当点M与点N之间的距离最小时,点M的坐标(直接写出结果即可).
参考答案
一、选择题(本大题共6小题,共24分)
1.用配方法解一元二次方程x2﹣6x﹣7=0,则方程变形为( )
A.(x﹣6)2=43 B.(x+6)2=43 C.(x﹣3)2=16 D.(x+3)2=16
【分析】首先进行移项变形成x2﹣6x=7,两边同时加上9,则左边是一个完全平方式,右边是一个常数,即可完成配方.
解:∵x2﹣6x﹣7=0,
∴x2﹣6x=7,
∴x2﹣6x+9=7+9,
∴(x﹣3)2=16.
故选:C.
2.已知Rt△ABC中,∠C=90°,且BC=AB,则∠A等于( )
A.30° B.45° C.60° D.不能确定
【分析】逆用在直角三角形中,30°角所对的直角边等于斜边的一半解答即可.
解:如图,∵∠C=90°,BC=AB,
∴∠A=30°.
故选:A.
3.下列各式中,计算错误的是( )
A. B.
C.(a≥0) D.
【分析】A、根据二次根式的乘法法则计算即可判定;
B、根据二次根式的加减法则计算即可判定;
C、根据二次根式的加减法则计算即可判定;
D、根号二次根式的除法法则计算即可判定.
解:A、,故选项正确;
B、,故选项错误;
C、(a≥0),故选项正确;
D、,故选项正确.
故选:B.
4.下列命题中真命题是( )
A.如果两个直角三角形的两条边相等,那么这两个直角三角形全等
B.如果两个直角三角形的一条边和一个锐角对应相等,那么这两个直角三角形全等
C.如果两个直角三角形的两个角对应相等,那么这两个直角三角形全等
D.如果两个直角三角形的一条直角边和斜边对应相等,那么这两个直角三角形全等
【分析】根据直角三角形全等的判定进行判断即可.
解:A、如果两个直角三角形的两条边相等,那么这两个直角三角形不一定全等,故此选项错误;
B、如果两个直角三角形的一条边和一个锐角对应相等,那么这两个直角三角形不一定全等,故此选项错误;
C、如果两个直角三角形的两个角对应相等,那么这两个直角三角形不一定全等,故此选项错误;
D、如果两个直角三角形的一条直角边和斜边对应相等,那么这两个直角三角形全等.此选项正确.
故选:D.
5.如图,A,C是函数的图象上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则S1和S2的大小关系是( )
A.S1>S2 B.S1<S2
C.S1=S2 D.由A,C两点的位置确定
【分析】根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.
解:结合题意可得:A、C都在双曲线y=上,
由反比例函数系数k的几何意义有S1=S2.
故选:C.
6.如图1,在平行四边形ABCD中,AD=5cm,CD=3cm,AC⊥CD,点P从点C出发,以1cm/s的速度沿C→D→A匀速运动,点M从点B出发,以相同的速度沿B→C匀速运动,其中一点停止时,另一点随之停止运动,图2是△PMC的面积S(cm2)随时间t(s)变化的函数图象,若a秒与b秒时△PMC的面积均为cm2,则b﹣a的值为( )
A. B. C.3 D.
【分析】过点A作AQ⊥BC于点Q,过点P作PN⊥BC,交BC的延长线于点N,由此可得AQ的长度;根据点P和点Q的运动可知,0≤t≤5;点P的运动分两种情况,当点P在边CD上运动时,S与t的函数图象为图中的曲线OEF,表达出△PMC的面积,列出等式即可求出a的值;当点P在边AD上运动时,S与t之间的函数图象为题中的曲线FGH,表达出三角形PMC的面积,列出等式即可求出b的值,最后即可求出b﹣a的值.
解:∵AC⊥CD,
∴∠ACD=90°,
∴AC===4cm,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=3cm,BC=AD=5cm,
∴∠BAC=90°.
①当点P在边CD上运动时,S与t的函数图象为图中的曲线OEF,
此时CM=BC﹣BM=(5﹣t)cm,PC=tcm,0≤t≤3,
过点A作AQ⊥BC于点Q,过点P作PN⊥BC,交BC的延长线于点N,
∵S△ABC=BC AQ=AB AC,即×5×AQ=×3×4,
∴AQ=cm.
∵AB∥CD,
∴∠B=∠PCN,
∵∠AQB=∠PNC=90°,
∴△AQB∽△PNC,
∴=,即,解得PN=t,
∴S=CM PN=×(5﹣t)×t=t(5﹣t),
根据题意,得t(5﹣t)=,解得t=1或t=4(舍),
∴a=1.
②当点P在边AD上运动时,S与t之间的函数图象为题中的曲线FGH,
此时CM=BC﹣BM=(5﹣t)cm,3<t≤5,
∵AD∥BC,
∴点P到BC的距离与点A到BC的距离相等,即边MC上的高位AQ=cm.
∴S=CM AQ=×(5﹣t)×=(5﹣t).
根据题意可得,(5﹣t)=,解得t=,
∴b=,
∴b﹣a=﹣1=.
故选:B.
二、填空题(本大题共12小题,共48分)
7.已知函数y=,则自变量x的取值范围是 x>1 .
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
解:由题意得,x﹣1>0,
解得x>1.
故答案为:x>1.
8.已知函数,则= .
【分析】首先把x=代入,然后进行求值即可.
解:f()==3.
故答案是:3.
9.方程x2=2x的根为 x1=0,x2=2 .
【分析】移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
解:x2=2x,
x2﹣2x=0,
x(x﹣2)=0,
x=0,或x﹣2=0,
x1=0,x2=2,
故答案为:x1=0,x2=2.
10.已知函数的图象经过点(2,5),则实数k= 10 .
【分析】因为函数经过一定点,将此点坐标(2,5)代入函数解析式y=(k≠0)即可求得k的值.
解:因为函数经过点P(2,5),
∴5=,
解得k=10.
故答案为:10.
11.命题“同旁内角互补,两直线平行”中,题设是 两条直线被第三条直线所截的同旁内角互补 ,结论是 这两条直线平行 ;此命题是 真 (填“真命题”或“假命题”)
【分析】把命题写成“如果…那么…”形式,则如果后面为题设,那么后面为结论.然后根据平行线的判定方法可判断命题为真命题.
解:命题“同旁内角互补,两直线平行”中,题设是两条直线被第三条直线所截的同旁内角互补,结论是 这两条直线平行;此命题是真命题.
故答案为如果两条直线被第三条直线所截的同旁内角互补,这两条直线平行,真.
12.已知关于x的方程(m﹣2)x2﹣2x+1=0有实数根,则实数m的取值范围是 m≤3 .
【分析】分类讨论:当m﹣2=0,解m=2,原方程变形为一元一次方程,有一个实数解;当m﹣2≠0,即m≠2,方程为一元二次方程,根据判别式的意义得到Δ=4﹣4(m﹣2)=﹣4m+12>0,然后综合两种情况即可.
解:当m﹣2=0,解m=2,原方程变形为﹣2x+1=0,解得x=;
当m﹣2≠0,即m≠2,则Δ=4﹣4(m﹣2)=﹣4m+12≥0,
解得:m≤3,
即当m≤3,且m≠2时,原方程有两个不相等实数根,
所以m的取值范围为:m≤3.
故答案为:m≤3.
13.已知实数a在数轴上的位置如图所示,化简= 1﹣a .
【分析】本题需先根据a在数轴上的位置,得出a<﹣1,再根据二次根式的性质与化简,即可求出答案.
解:根据a在数轴上的位置,得a<﹣1,
∴=1﹣a.
故答案为:1﹣a.
14.已知函数y=2x与的图象的一个交点坐标是(1,2),则它们的图象的另一个交点的坐标是 (﹣1,﹣2) .
【分析】反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称.
解:∵点(1,2)关于原点对称的点是(﹣1,﹣2),
∴所求的点的坐标为(﹣1,﹣2).
故答案是:(﹣1,﹣2).
15.如图,已知Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,现将△ABC进行折叠,使顶点A、B重合,则折痕DE= 1.875 cm.
【分析】根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
解:在直角△ABC中AB===5cm.则AE=AB÷2=2.5cm.
设DE=x,易得△ADE∽△ABC,
故有=;
∴=;
解可得x=1.875.
故答案为:1.875.
16.已知直角三角形的两边长为x,y,且满足|x2﹣4|+=0,则第三边长为 2,或 .
【分析】首先利用绝对值以及算术平方根的性质得出x,y的值,再利用分类讨论结合勾股定理求出第三边长.
解:∵x、y为直角三角形的两边的长,满足|x2﹣4|+=0,
∴x2﹣4=0,y2﹣5y+6=0,
解得:x1=2,x2=﹣2(不合题意舍去),y1=2,y2=3,
当直角边长为:2,2,则第三边长为:2,
当直角边长为:2,3,则第三边长为:,
当直角边长为2,斜边长为3,则第三边长为:.
故答案为:2,或.
17.如图,已知在△ABC中,AB=AC=6,∠BAC=30°,将△ABC沿AC翻折,使点B落在点D处,延长AD与BC的延长线相交于点E,则DE的长为 3﹣3 .
【分析】过C作CH⊥AE于H,由等腰三角形的性质和三角形内角和定理得∠B=∠ACB=75°,再由翻折的性质得AD=AB=6,∠CAD=∠BAC=30°,然后由含30°角的直角三角形的性质得CH=AC=3,则AH=3,得DH=AD﹣AH=6﹣3,最后证EH=CH=3,即可求解.
解:过C作CH⊥AE于H,如图所示:
∵AB=AC=6,
∴∠B=∠ACB=×(180°﹣∠BAC)=×(180°﹣30°)=75°.
∵将△ABC绕点A逆时针旋转,使点B落在点C处,此时点C落在点D处,
∴AD=AB=6,∠CAD=∠BAC=30°,
∵∠ACB=∠CAD+∠E,
∴∠E=75°﹣30°=45°.
在Rt△ACH中,∠CAH=30°,
∴CH=AC=3,
∴AH===3,
∴DH=AD﹣AH=6﹣3,
在Rt△CEH中,∠E=45°,
∴△CEH是等腰直角三角形,
∴EH=CH=3,
∴DE=EH﹣DH=3﹣(6﹣3)=3﹣3.
故答案为:3﹣3.
18.已知在△ABC中,∠C=90°,AC=3,BC=4,在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,若旋转后点C的对应点C′落直线AB上,那么AA′的长为 或3 .
【分析】分两种情况:①当C′点在线段AB上,②当C′点在线段AB的延长线上,由勾股定理可求出答案.
解:①当C′点在线段AB上,如图1,连接AA′,
∵∠C=90°,AC=3,BC=4,
∴AB===5,
∵在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,
∴BC′=BC=4,A′C′=AC=3,
∴AC′=AB﹣BC′=1,
∴AA'===;
②当C′点在线段AB的延长线上,如图2,连接AA′,
∵在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,
∴BC′=BC=4,A′C′=AC=3,
∴AC′=AB+BC′=9,
∴AA'===3.
综合以上可得AA′的长为或3.
故答案为或3.
三、解答题(本大题共7小题,共78分)
19.已知,求代数式20x2+55xy+20y2的值.
【分析】直接利用分母有理化将原式化简,再将多项式变形进而代入得出答案.
解:∵x==(﹣)2=5﹣2,
y==(+)2=5+2,
∴原式=20x2+40xy+20y2+15xy
=20(x2+2xy+y2)+15xy
=20(x+y)2+15xy
=20×(5﹣2+5+2)2+15×(5﹣2)(5+2)
=20×102+15×(25﹣24)
=2000+15
=2015.
20.若实数m,n满足|m﹣2|+=0,请用配方法解关于x的一元二次方程x2+mx+n=0.
【分析】直接利用非负数的性质得出m,n的值,进而代入方程利用配方法解方程得出答案.
解:∵|m﹣2|+=0,
∴,
解得:,
故x2+mx+n=0为:x2+2x﹣1=0,
则x2+2x=1
(x+1)2=2,
故x+1=±,
解得:x1=﹣1+,x2=﹣1﹣.
21.如图,已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等.(尺规作图,不写作法,保留作图痕迹)
【分析】根据角平分线的性质(角平分线上的点到两边的距离相等)和垂线的性质(垂直于线段并过线段中点的线上的点到两顶点的距离相等)进行解题.
解:如图所示:
,
点P即为所求.
22.为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.
【分析】(1)设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,则,即可求解;
(2)点A(5,10),则反比例函数表达式为y=,当x=55时,y=<1,即可求解.
解:(1)设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,
则,解得,
故校医完成一间办公室和一间教室的药物喷洒各要3min和5min;
(2)一间教室的药物喷洒时间为5min,则11个房间需要55min,
当x=5时,y=2x=10,故点A(5,10),
设反比例函数表达式为:y=,将点A的坐标代入上式并解得:k=50,
故反比例函数表达式为y=,
当x=55时,y=<1,
故一班学生能安全进入教室.
23.已知△ABC中,AD是∠BAC的平分线,且AD=AB,过点C作AD的垂线,交AD的延长线于点H.
(1)如图1,若∠BAC=60°.
①直接写出∠B和∠ACB的度数;
②若AB=2,求AC和AH的长;
(2)如图2,用等式表示线段AH与AB+AC之间的数量关系,并证明.
【分析】(1)①先根据角平分线的定义可得:∠BAD=∠CAD=30°,由等腰三角形的性质得:∠B=75°,最后利用三角形内角和可得∠ACB=45°;
②如图1,作高线DE,在Rt△ADE中,由∠DAC=30°,AB=AD=2可得DE=1,AE=,在Rt△CDE中,由∠ACD=45°,DE=1,可得EC=1,AC=+1,同理可得AH的长;
(2)如图2,作辅助线,构建等腰三角形,易证△ACH≌△AFH,则AC=AF,HC=HF,根据平行线的性质和
等腰三角形的性质得:AG=AH,再由线段的和可得结论.
解:(1)①∵AD平分∠BAC,∠BAC=60°,
∴∠BAD=∠CAD=30°,
∵AB=AD,
∴∠B==75°,
∴∠ACB=180°﹣60°﹣75°=45°,
②如图1,过D作DE⊥AC交AC于点E,
在Rt△ADE中,∵∠DAC=30°,AB=AD=2,
∴DE=1,AE=,
在Rt△CDE中,∵∠ACD=45°,DE=1,
∴EC=1,
∴AC=+1,
在Rt△ACH中,∵∠DAC=30°,
∴CH=AC=,
∴AH===;
(2)线段AH与AB+AC之间的数量关系:2AH=AB+AC.
证明:如图2,延长AB和CH交于点F,取BF的中点G,连接GH.
易证△ACH≌△AFH,
∴AC=AF,HC=HF,
∴GH∥BC,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠AGH=∠AHG,
∴AG=AH,
∴AB+AC=AB+AF=2AB+BF=2(AB+BG)=2AG=2AH.
24.已知反比例函数y=的图象经过点A(﹣,1).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;
(3)已知点P(m,m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2n+9的值.
【分析】(1)由于反比例函数y=的图象经过点A(﹣,1),运用待定系数法即可求出此反比例函数的解析式;
(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;
(3)把点P(m,m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2﹣2n+9的值.
解:(1)由题意得1=,解得k=﹣,
∴反比例函数的解析式为y=﹣;
(2)过点A作x轴的垂线交x轴于点C.
在Rt△AOC中,OC=,AC=1,
∴OA==2,∠AOC=30°,
∵将线段OA绕O点顺时针旋转30°得到线段OB,
∴∠AOB=30°,OB=OA=2,
∴∠BOC=60°.
过点B作x轴的垂线交x轴于点D.
在Rt△BOD中,BD=OB sin∠BOD=,OD=OB=1,
∴B点坐标为(﹣1,),
将x=﹣1代入y=﹣中,得y=,
∴点B(﹣1,)在反比例函数y=﹣的图象上.
(3)由y=﹣得xy=﹣,
∵点P(m,m+6)在反比例函数y=﹣的图象上,其中m<0,
∴m(m+6)=﹣,
∴m2+2m+1=0,
∵PQ⊥x轴,∴Q点的坐标为(m,n).
∵△OQM的面积是,
∴OM QM=,
∵m<0,∴mn=﹣1,
∴m2n2+2mn2+n2=0,
∴n2﹣2n=﹣1,
∴n2﹣2n+9=8.
25.在平面直角坐标系中,两个形状、大小完全相同的三角板OBC,DEF,按如图所示的位置摆放,O为原点,点B(12,0),点B与点D重合,边OB与边DE都在x轴上.其中,∠C=∠DEF=90°,∠OBC=∠F=30°.
(1)如图①,求点C坐标;
(2)现固定三角板DEF,将三角板OBC沿x轴正方向平移,得到△O′B′C′,当点O′落点D上时停止运动.设三角板平移的距离为x,两个三角板重叠部分的面积为y.求y关于x的函数解析式,并写出自变量x的取值范围;
(3)在(2)条件下,设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,当点M与点N之间的距离最小时,点M的坐标(直接写出结果即可).
【分析】(1)如图①所示:过点C作CG⊥AB于G点,解直角三角形即可得到结论;
(2)①当0≤x<6时,如图②所示.
②当6≤x≤12时,如图③所示,根据三角形的面积公式即可得到结论;
(3)如图④所示,作NG⊥DE于G点,当点M在NG上时MN最短,根据三角形的中位线定理得到NG=EF=3,解直角三角形即可得到结论.
解:(1)如图①所示:过点C作CG⊥AB于G点,
∵B(12,0),得OB=12,
在Rt△OBC中,由OB=12,∠OBC=30°,得OC=6,
∴∠COB=60°,
在Rt△OCG中,OG=OC cos60°=3,
∴CG=OC sin60°=,
∴C (3,);
(2)①当0≤x<6时,如图②所示.
∠GDE=60°,∠GB′D=30°,DB′=x,得DG=,B′G=,
重叠部分的面积为y=DG B′G=×x×=
②当6≤x≤12时,如图③所示,
B′D=x,DG=x,B′G=,B′E=x﹣6,
EH=.
重叠部分的面积为y=S△B′DG﹣S△B′EH=DG B′G﹣B′E EH,
即y=×x×﹣(x﹣6)
化简,得y=;
综上所述:;
(3)如图④所示,
∵EF=BC=OB=6,
作NG⊥DE于G点,
当点M在NG上时MN最短,
∵点N为DF的中点,NG∥EF,
∴NG是△DEF的中位线,
∴NG=EF=3,
∵点M为边BC的中点,
∴MB=CB=3,∠B=30°,
∴MG=MB=,
∵DG=DN=3,
∴OO′=OD+DG=12+3=15,
∴M .
一、选择题(本大题共6小题,共24分)
1.用配方法解一元二次方程x2﹣6x﹣7=0,则方程变形为( )
A.(x﹣6)2=43 B.(x+6)2=43 C.(x﹣3)2=16 D.(x+3)2=16
2.已知Rt△ABC中,∠C=90°,且BC=AB,则∠A等于( )
A.30° B.45° C.60° D.不能确定
3.下列各式中,计算错误的是( )
A. B.
C.(a≥0) D.
4.下列命题中真命题是( )
A.如果两个直角三角形的两条边相等,那么这两个直角三角形全等
B.如果两个直角三角形的一条边和一个锐角对应相等,那么这两个直角三角形全等
C.如果两个直角三角形的两个角对应相等,那么这两个直角三角形全等
D.如果两个直角三角形的一条直角边和斜边对应相等,那么这两个直角三角形全等
5.如图,A,C是函数的图象上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则S1和S2的大小关系是( )
A.S1>S2 B.S1<S2
C.S1=S2 D.由A,C两点的位置确定
6.如图1,在平行四边形ABCD中,AD=5cm,CD=3cm,AC⊥CD,点P从点C出发,以1cm/s的速度沿C→D→A匀速运动,点M从点B出发,以相同的速度沿B→C匀速运动,其中一点停止时,另一点随之停止运动,图2是△PMC的面积S(cm2)随时间t(s)变化的函数图象,若a秒与b秒时△PMC的面积均为cm2,则b﹣a的值为( )
A. B. C.3 D.
二、填空题(本大题共12小题,共48分)
7.已知函数y=,则自变量x的取值范围是 .
8.已知函数,则= .
9.方程x2=2x的根为 .
10.已知函数的图象经过点(2,5),则实数k= .
11.命题“同旁内角互补,两直线平行”中,题设是 ,结论是 ;此命题是 (填“真命题”或“假命题”)
12.已知关于x的方程(m﹣2)x2﹣2x+1=0有实数根,则实数m的取值范围是 .
13.已知实数a在数轴上的位置如图所示,化简= .
14.已知函数y=2x与的图象的一个交点坐标是(1,2),则它们的图象的另一个交点的坐标是 .
15.如图,已知Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,现将△ABC进行折叠,使顶点A、B重合,则折痕DE= cm.
16.已知直角三角形的两边长为x,y,且满足|x2﹣4|+=0,则第三边长为 .
17.如图,已知在△ABC中,AB=AC=6,∠BAC=30°,将△ABC沿AC翻折,使点B落在点D处,延长AD与BC的延长线相交于点E,则DE的长为 .
18.已知在△ABC中,∠C=90°,AC=3,BC=4,在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,若旋转后点C的对应点C′落直线AB上,那么AA′的长为 .
三、解答题(本大题共7小题,共78分)
19.已知,求代数式20x2+55xy+20y2的值.
20.若实数m,n满足|m﹣2|+=0,请用配方法解关于x的一元二次方程x2+mx+n=0.
21.如图,已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等.(尺规作图,不写作法,保留作图痕迹)
22.为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.
23.已知△ABC中,AD是∠BAC的平分线,且AD=AB,过点C作AD的垂线,交AD的延长线于点H.
(1)如图1,若∠BAC=60°.
①直接写出∠B和∠ACB的度数;
②若AB=2,求AC和AH的长;
(2)如图2,用等式表示线段AH与AB+AC之间的数量关系,并证明.
24.已知反比例函数y=的图象经过点A(﹣,1).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;
(3)已知点P(m,m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2n+9的值.
25.在平面直角坐标系中,两个形状、大小完全相同的三角板OBC,DEF,按如图所示的位置摆放,O为原点,点B(12,0),点B与点D重合,边OB与边DE都在x轴上.其中,∠C=∠DEF=90°,∠OBC=∠F=30°.
(1)如图①,求点C坐标;
(2)现固定三角板DEF,将三角板OBC沿x轴正方向平移,得到△O′B′C′,当点O′落点D上时停止运动.设三角板平移的距离为x,两个三角板重叠部分的面积为y.求y关于x的函数解析式,并写出自变量x的取值范围;
(3)在(2)条件下,设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,当点M与点N之间的距离最小时,点M的坐标(直接写出结果即可).
参考答案
一、选择题(本大题共6小题,共24分)
1.用配方法解一元二次方程x2﹣6x﹣7=0,则方程变形为( )
A.(x﹣6)2=43 B.(x+6)2=43 C.(x﹣3)2=16 D.(x+3)2=16
【分析】首先进行移项变形成x2﹣6x=7,两边同时加上9,则左边是一个完全平方式,右边是一个常数,即可完成配方.
解:∵x2﹣6x﹣7=0,
∴x2﹣6x=7,
∴x2﹣6x+9=7+9,
∴(x﹣3)2=16.
故选:C.
2.已知Rt△ABC中,∠C=90°,且BC=AB,则∠A等于( )
A.30° B.45° C.60° D.不能确定
【分析】逆用在直角三角形中,30°角所对的直角边等于斜边的一半解答即可.
解:如图,∵∠C=90°,BC=AB,
∴∠A=30°.
故选:A.
3.下列各式中,计算错误的是( )
A. B.
C.(a≥0) D.
【分析】A、根据二次根式的乘法法则计算即可判定;
B、根据二次根式的加减法则计算即可判定;
C、根据二次根式的加减法则计算即可判定;
D、根号二次根式的除法法则计算即可判定.
解:A、,故选项正确;
B、,故选项错误;
C、(a≥0),故选项正确;
D、,故选项正确.
故选:B.
4.下列命题中真命题是( )
A.如果两个直角三角形的两条边相等,那么这两个直角三角形全等
B.如果两个直角三角形的一条边和一个锐角对应相等,那么这两个直角三角形全等
C.如果两个直角三角形的两个角对应相等,那么这两个直角三角形全等
D.如果两个直角三角形的一条直角边和斜边对应相等,那么这两个直角三角形全等
【分析】根据直角三角形全等的判定进行判断即可.
解:A、如果两个直角三角形的两条边相等,那么这两个直角三角形不一定全等,故此选项错误;
B、如果两个直角三角形的一条边和一个锐角对应相等,那么这两个直角三角形不一定全等,故此选项错误;
C、如果两个直角三角形的两个角对应相等,那么这两个直角三角形不一定全等,故此选项错误;
D、如果两个直角三角形的一条直角边和斜边对应相等,那么这两个直角三角形全等.此选项正确.
故选:D.
5.如图,A,C是函数的图象上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则S1和S2的大小关系是( )
A.S1>S2 B.S1<S2
C.S1=S2 D.由A,C两点的位置确定
【分析】根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.
解:结合题意可得:A、C都在双曲线y=上,
由反比例函数系数k的几何意义有S1=S2.
故选:C.
6.如图1,在平行四边形ABCD中,AD=5cm,CD=3cm,AC⊥CD,点P从点C出发,以1cm/s的速度沿C→D→A匀速运动,点M从点B出发,以相同的速度沿B→C匀速运动,其中一点停止时,另一点随之停止运动,图2是△PMC的面积S(cm2)随时间t(s)变化的函数图象,若a秒与b秒时△PMC的面积均为cm2,则b﹣a的值为( )
A. B. C.3 D.
【分析】过点A作AQ⊥BC于点Q,过点P作PN⊥BC,交BC的延长线于点N,由此可得AQ的长度;根据点P和点Q的运动可知,0≤t≤5;点P的运动分两种情况,当点P在边CD上运动时,S与t的函数图象为图中的曲线OEF,表达出△PMC的面积,列出等式即可求出a的值;当点P在边AD上运动时,S与t之间的函数图象为题中的曲线FGH,表达出三角形PMC的面积,列出等式即可求出b的值,最后即可求出b﹣a的值.
解:∵AC⊥CD,
∴∠ACD=90°,
∴AC===4cm,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=3cm,BC=AD=5cm,
∴∠BAC=90°.
①当点P在边CD上运动时,S与t的函数图象为图中的曲线OEF,
此时CM=BC﹣BM=(5﹣t)cm,PC=tcm,0≤t≤3,
过点A作AQ⊥BC于点Q,过点P作PN⊥BC,交BC的延长线于点N,
∵S△ABC=BC AQ=AB AC,即×5×AQ=×3×4,
∴AQ=cm.
∵AB∥CD,
∴∠B=∠PCN,
∵∠AQB=∠PNC=90°,
∴△AQB∽△PNC,
∴=,即,解得PN=t,
∴S=CM PN=×(5﹣t)×t=t(5﹣t),
根据题意,得t(5﹣t)=,解得t=1或t=4(舍),
∴a=1.
②当点P在边AD上运动时,S与t之间的函数图象为题中的曲线FGH,
此时CM=BC﹣BM=(5﹣t)cm,3<t≤5,
∵AD∥BC,
∴点P到BC的距离与点A到BC的距离相等,即边MC上的高位AQ=cm.
∴S=CM AQ=×(5﹣t)×=(5﹣t).
根据题意可得,(5﹣t)=,解得t=,
∴b=,
∴b﹣a=﹣1=.
故选:B.
二、填空题(本大题共12小题,共48分)
7.已知函数y=,则自变量x的取值范围是 x>1 .
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
解:由题意得,x﹣1>0,
解得x>1.
故答案为:x>1.
8.已知函数,则= .
【分析】首先把x=代入,然后进行求值即可.
解:f()==3.
故答案是:3.
9.方程x2=2x的根为 x1=0,x2=2 .
【分析】移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
解:x2=2x,
x2﹣2x=0,
x(x﹣2)=0,
x=0,或x﹣2=0,
x1=0,x2=2,
故答案为:x1=0,x2=2.
10.已知函数的图象经过点(2,5),则实数k= 10 .
【分析】因为函数经过一定点,将此点坐标(2,5)代入函数解析式y=(k≠0)即可求得k的值.
解:因为函数经过点P(2,5),
∴5=,
解得k=10.
故答案为:10.
11.命题“同旁内角互补,两直线平行”中,题设是 两条直线被第三条直线所截的同旁内角互补 ,结论是 这两条直线平行 ;此命题是 真 (填“真命题”或“假命题”)
【分析】把命题写成“如果…那么…”形式,则如果后面为题设,那么后面为结论.然后根据平行线的判定方法可判断命题为真命题.
解:命题“同旁内角互补,两直线平行”中,题设是两条直线被第三条直线所截的同旁内角互补,结论是 这两条直线平行;此命题是真命题.
故答案为如果两条直线被第三条直线所截的同旁内角互补,这两条直线平行,真.
12.已知关于x的方程(m﹣2)x2﹣2x+1=0有实数根,则实数m的取值范围是 m≤3 .
【分析】分类讨论:当m﹣2=0,解m=2,原方程变形为一元一次方程,有一个实数解;当m﹣2≠0,即m≠2,方程为一元二次方程,根据判别式的意义得到Δ=4﹣4(m﹣2)=﹣4m+12>0,然后综合两种情况即可.
解:当m﹣2=0,解m=2,原方程变形为﹣2x+1=0,解得x=;
当m﹣2≠0,即m≠2,则Δ=4﹣4(m﹣2)=﹣4m+12≥0,
解得:m≤3,
即当m≤3,且m≠2时,原方程有两个不相等实数根,
所以m的取值范围为:m≤3.
故答案为:m≤3.
13.已知实数a在数轴上的位置如图所示,化简= 1﹣a .
【分析】本题需先根据a在数轴上的位置,得出a<﹣1,再根据二次根式的性质与化简,即可求出答案.
解:根据a在数轴上的位置,得a<﹣1,
∴=1﹣a.
故答案为:1﹣a.
14.已知函数y=2x与的图象的一个交点坐标是(1,2),则它们的图象的另一个交点的坐标是 (﹣1,﹣2) .
【分析】反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称.
解:∵点(1,2)关于原点对称的点是(﹣1,﹣2),
∴所求的点的坐标为(﹣1,﹣2).
故答案是:(﹣1,﹣2).
15.如图,已知Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,现将△ABC进行折叠,使顶点A、B重合,则折痕DE= 1.875 cm.
【分析】根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
解:在直角△ABC中AB===5cm.则AE=AB÷2=2.5cm.
设DE=x,易得△ADE∽△ABC,
故有=;
∴=;
解可得x=1.875.
故答案为:1.875.
16.已知直角三角形的两边长为x,y,且满足|x2﹣4|+=0,则第三边长为 2,或 .
【分析】首先利用绝对值以及算术平方根的性质得出x,y的值,再利用分类讨论结合勾股定理求出第三边长.
解:∵x、y为直角三角形的两边的长,满足|x2﹣4|+=0,
∴x2﹣4=0,y2﹣5y+6=0,
解得:x1=2,x2=﹣2(不合题意舍去),y1=2,y2=3,
当直角边长为:2,2,则第三边长为:2,
当直角边长为:2,3,则第三边长为:,
当直角边长为2,斜边长为3,则第三边长为:.
故答案为:2,或.
17.如图,已知在△ABC中,AB=AC=6,∠BAC=30°,将△ABC沿AC翻折,使点B落在点D处,延长AD与BC的延长线相交于点E,则DE的长为 3﹣3 .
【分析】过C作CH⊥AE于H,由等腰三角形的性质和三角形内角和定理得∠B=∠ACB=75°,再由翻折的性质得AD=AB=6,∠CAD=∠BAC=30°,然后由含30°角的直角三角形的性质得CH=AC=3,则AH=3,得DH=AD﹣AH=6﹣3,最后证EH=CH=3,即可求解.
解:过C作CH⊥AE于H,如图所示:
∵AB=AC=6,
∴∠B=∠ACB=×(180°﹣∠BAC)=×(180°﹣30°)=75°.
∵将△ABC绕点A逆时针旋转,使点B落在点C处,此时点C落在点D处,
∴AD=AB=6,∠CAD=∠BAC=30°,
∵∠ACB=∠CAD+∠E,
∴∠E=75°﹣30°=45°.
在Rt△ACH中,∠CAH=30°,
∴CH=AC=3,
∴AH===3,
∴DH=AD﹣AH=6﹣3,
在Rt△CEH中,∠E=45°,
∴△CEH是等腰直角三角形,
∴EH=CH=3,
∴DE=EH﹣DH=3﹣(6﹣3)=3﹣3.
故答案为:3﹣3.
18.已知在△ABC中,∠C=90°,AC=3,BC=4,在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,若旋转后点C的对应点C′落直线AB上,那么AA′的长为 或3 .
【分析】分两种情况:①当C′点在线段AB上,②当C′点在线段AB的延长线上,由勾股定理可求出答案.
解:①当C′点在线段AB上,如图1,连接AA′,
∵∠C=90°,AC=3,BC=4,
∴AB===5,
∵在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,
∴BC′=BC=4,A′C′=AC=3,
∴AC′=AB﹣BC′=1,
∴AA'===;
②当C′点在线段AB的延长线上,如图2,连接AA′,
∵在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,
∴BC′=BC=4,A′C′=AC=3,
∴AC′=AB+BC′=9,
∴AA'===3.
综合以上可得AA′的长为或3.
故答案为或3.
三、解答题(本大题共7小题,共78分)
19.已知,求代数式20x2+55xy+20y2的值.
【分析】直接利用分母有理化将原式化简,再将多项式变形进而代入得出答案.
解:∵x==(﹣)2=5﹣2,
y==(+)2=5+2,
∴原式=20x2+40xy+20y2+15xy
=20(x2+2xy+y2)+15xy
=20(x+y)2+15xy
=20×(5﹣2+5+2)2+15×(5﹣2)(5+2)
=20×102+15×(25﹣24)
=2000+15
=2015.
20.若实数m,n满足|m﹣2|+=0,请用配方法解关于x的一元二次方程x2+mx+n=0.
【分析】直接利用非负数的性质得出m,n的值,进而代入方程利用配方法解方程得出答案.
解:∵|m﹣2|+=0,
∴,
解得:,
故x2+mx+n=0为:x2+2x﹣1=0,
则x2+2x=1
(x+1)2=2,
故x+1=±,
解得:x1=﹣1+,x2=﹣1﹣.
21.如图,已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等.(尺规作图,不写作法,保留作图痕迹)
【分析】根据角平分线的性质(角平分线上的点到两边的距离相等)和垂线的性质(垂直于线段并过线段中点的线上的点到两顶点的距离相等)进行解题.
解:如图所示:
,
点P即为所求.
22.为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.
【分析】(1)设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,则,即可求解;
(2)点A(5,10),则反比例函数表达式为y=,当x=55时,y=<1,即可求解.
解:(1)设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,
则,解得,
故校医完成一间办公室和一间教室的药物喷洒各要3min和5min;
(2)一间教室的药物喷洒时间为5min,则11个房间需要55min,
当x=5时,y=2x=10,故点A(5,10),
设反比例函数表达式为:y=,将点A的坐标代入上式并解得:k=50,
故反比例函数表达式为y=,
当x=55时,y=<1,
故一班学生能安全进入教室.
23.已知△ABC中,AD是∠BAC的平分线,且AD=AB,过点C作AD的垂线,交AD的延长线于点H.
(1)如图1,若∠BAC=60°.
①直接写出∠B和∠ACB的度数;
②若AB=2,求AC和AH的长;
(2)如图2,用等式表示线段AH与AB+AC之间的数量关系,并证明.
【分析】(1)①先根据角平分线的定义可得:∠BAD=∠CAD=30°,由等腰三角形的性质得:∠B=75°,最后利用三角形内角和可得∠ACB=45°;
②如图1,作高线DE,在Rt△ADE中,由∠DAC=30°,AB=AD=2可得DE=1,AE=,在Rt△CDE中,由∠ACD=45°,DE=1,可得EC=1,AC=+1,同理可得AH的长;
(2)如图2,作辅助线,构建等腰三角形,易证△ACH≌△AFH,则AC=AF,HC=HF,根据平行线的性质和
等腰三角形的性质得:AG=AH,再由线段的和可得结论.
解:(1)①∵AD平分∠BAC,∠BAC=60°,
∴∠BAD=∠CAD=30°,
∵AB=AD,
∴∠B==75°,
∴∠ACB=180°﹣60°﹣75°=45°,
②如图1,过D作DE⊥AC交AC于点E,
在Rt△ADE中,∵∠DAC=30°,AB=AD=2,
∴DE=1,AE=,
在Rt△CDE中,∵∠ACD=45°,DE=1,
∴EC=1,
∴AC=+1,
在Rt△ACH中,∵∠DAC=30°,
∴CH=AC=,
∴AH===;
(2)线段AH与AB+AC之间的数量关系:2AH=AB+AC.
证明:如图2,延长AB和CH交于点F,取BF的中点G,连接GH.
易证△ACH≌△AFH,
∴AC=AF,HC=HF,
∴GH∥BC,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠AGH=∠AHG,
∴AG=AH,
∴AB+AC=AB+AF=2AB+BF=2(AB+BG)=2AG=2AH.
24.已知反比例函数y=的图象经过点A(﹣,1).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;
(3)已知点P(m,m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2n+9的值.
【分析】(1)由于反比例函数y=的图象经过点A(﹣,1),运用待定系数法即可求出此反比例函数的解析式;
(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;
(3)把点P(m,m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2﹣2n+9的值.
解:(1)由题意得1=,解得k=﹣,
∴反比例函数的解析式为y=﹣;
(2)过点A作x轴的垂线交x轴于点C.
在Rt△AOC中,OC=,AC=1,
∴OA==2,∠AOC=30°,
∵将线段OA绕O点顺时针旋转30°得到线段OB,
∴∠AOB=30°,OB=OA=2,
∴∠BOC=60°.
过点B作x轴的垂线交x轴于点D.
在Rt△BOD中,BD=OB sin∠BOD=,OD=OB=1,
∴B点坐标为(﹣1,),
将x=﹣1代入y=﹣中,得y=,
∴点B(﹣1,)在反比例函数y=﹣的图象上.
(3)由y=﹣得xy=﹣,
∵点P(m,m+6)在反比例函数y=﹣的图象上,其中m<0,
∴m(m+6)=﹣,
∴m2+2m+1=0,
∵PQ⊥x轴,∴Q点的坐标为(m,n).
∵△OQM的面积是,
∴OM QM=,
∵m<0,∴mn=﹣1,
∴m2n2+2mn2+n2=0,
∴n2﹣2n=﹣1,
∴n2﹣2n+9=8.
25.在平面直角坐标系中,两个形状、大小完全相同的三角板OBC,DEF,按如图所示的位置摆放,O为原点,点B(12,0),点B与点D重合,边OB与边DE都在x轴上.其中,∠C=∠DEF=90°,∠OBC=∠F=30°.
(1)如图①,求点C坐标;
(2)现固定三角板DEF,将三角板OBC沿x轴正方向平移,得到△O′B′C′,当点O′落点D上时停止运动.设三角板平移的距离为x,两个三角板重叠部分的面积为y.求y关于x的函数解析式,并写出自变量x的取值范围;
(3)在(2)条件下,设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,当点M与点N之间的距离最小时,点M的坐标(直接写出结果即可).
【分析】(1)如图①所示:过点C作CG⊥AB于G点,解直角三角形即可得到结论;
(2)①当0≤x<6时,如图②所示.
②当6≤x≤12时,如图③所示,根据三角形的面积公式即可得到结论;
(3)如图④所示,作NG⊥DE于G点,当点M在NG上时MN最短,根据三角形的中位线定理得到NG=EF=3,解直角三角形即可得到结论.
解:(1)如图①所示:过点C作CG⊥AB于G点,
∵B(12,0),得OB=12,
在Rt△OBC中,由OB=12,∠OBC=30°,得OC=6,
∴∠COB=60°,
在Rt△OCG中,OG=OC cos60°=3,
∴CG=OC sin60°=,
∴C (3,);
(2)①当0≤x<6时,如图②所示.
∠GDE=60°,∠GB′D=30°,DB′=x,得DG=,B′G=,
重叠部分的面积为y=DG B′G=×x×=
②当6≤x≤12时,如图③所示,
B′D=x,DG=x,B′G=,B′E=x﹣6,
EH=.
重叠部分的面积为y=S△B′DG﹣S△B′EH=DG B′G﹣B′E EH,
即y=×x×﹣(x﹣6)
化简,得y=;
综上所述:;
(3)如图④所示,
∵EF=BC=OB=6,
作NG⊥DE于G点,
当点M在NG上时MN最短,
∵点N为DF的中点,NG∥EF,
∴NG是△DEF的中位线,
∴NG=EF=3,
∵点M为边BC的中点,
∴MB=CB=3,∠B=30°,
∴MG=MB=,
∵DG=DN=3,
∴OO′=OD+DG=12+3=15,
∴M .
同课章节目录
