24.1圆的有关性质 同步练习题 2021-2022学年人教版数学九年级上册(Word版含解析)
文档属性
| 名称 | 24.1圆的有关性质 同步练习题 2021-2022学年人教版数学九年级上册(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 324.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 14:20:13 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学上册《24.1圆的有关性质》同步练习题(附答案)
一.选择题(共12小题,满分36分)
1.已知⊙O中最长的弦长8cm,则⊙O的半径是( )
A.2cm B.4cm C.8cm D.16cm
2.下列说法中,正确的是( )
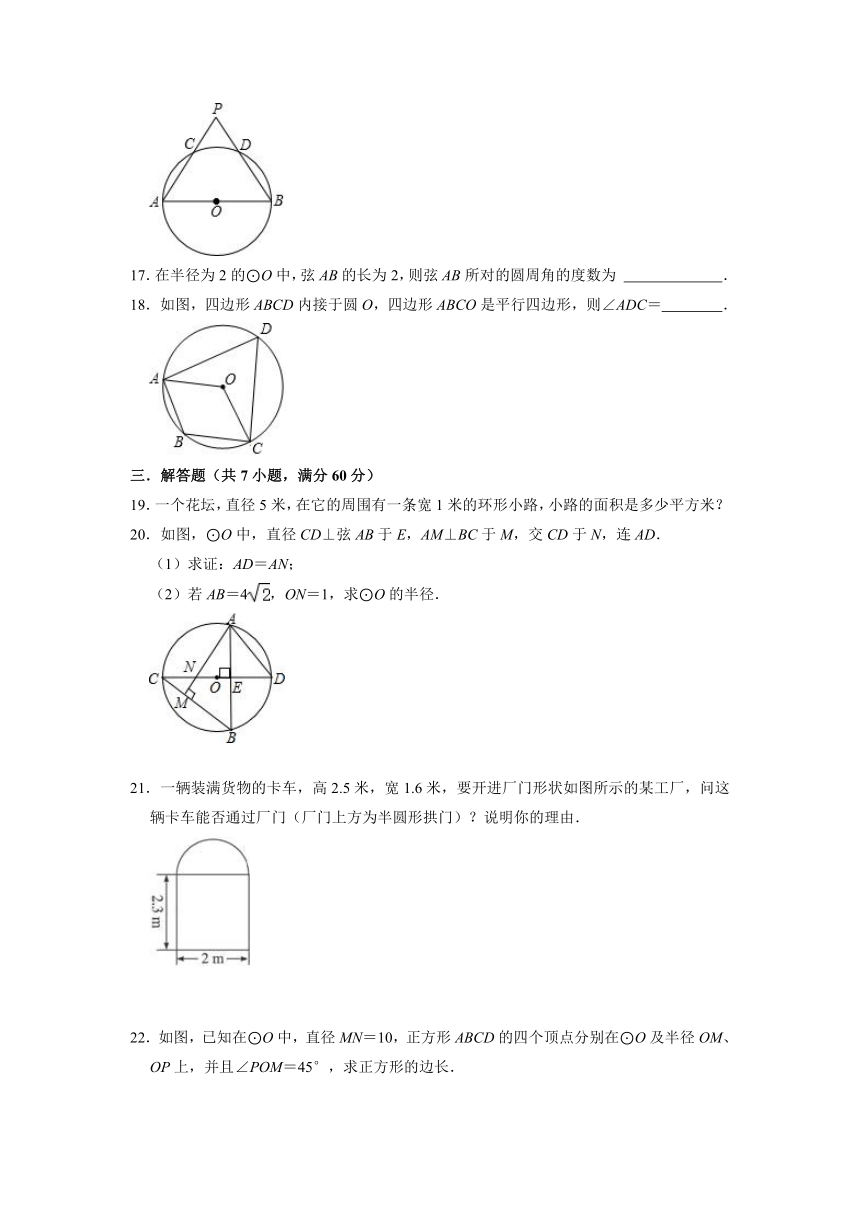
A.同一条弦所对的两条弧一定是等弧 B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形 D.三角形的外心到三角形各边的距离相等
3.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=4,CD=1,则EC的长为( )
A. B. C. D.4
4.如图,⊙O的半径为5,若OP=3,则经过点P的弦长可能是( )
A.3 B.6 C.9 D.12
5.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
6.一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
A.4.1米 B.4.0米 C.3.9米 D.3.8米
7.如图,AD是⊙O的直径,,若∠AOB=40°,则圆周角∠BPC的度数是( )
A.40° B.50° C.60° D.70°
8.下列语句,错误的是( )
A.直径是弦 B.弦的垂直平分线一定经过圆心
C.相等的圆心角所对的弧相等 D.平分弧的半径垂直于弧所对的弦
9.如图,AE是四边形ABCD外接圆⊙O的直径,AD=CD,∠B=50°,则∠DAE的度数为( )
A.70° B.65° C.60° D.55°
10.如图,AB是⊙O的直径,点C,D在直径AB一侧的圆上(异于A,B两点),点E在直径AB另一侧的圆上,若∠E=42°,∠A=60°,则∠B=( )
A.62° B.70° C.72° D.74°
11.如图,在圆内接四边形ABCD中,∠C=110°,则∠BOD的度数为( )
A.140° B.70° C.80° D.60°
12.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.60° B.55° C.50° D.45°
二.填空题(共6小题,满分24分)
13.对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(,2),顶点C、D在x轴上,OC=OD,且⊙P的半径为4.
(1)在P1(0,﹣2),P2(2,3),P3(﹣2,1)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
(2)如果点P在直线y=x+1上,且⊙P是矩形ABCD的“等距圆”,那么点P的坐标为 .
14.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径= 米.
15.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”.(1尺=10寸)则CD= .
16.如图,已知AB是⊙O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角等于 度.
17.在半径为2的⊙O中,弦AB的长为2,则弦AB所对的圆周角的度数为 .
18.如图,四边形ABCD内接于圆O,四边形ABCO是平行四边形,则∠ADC= .
三.解答题(共7小题,满分60分)
19.一个花坛,直径5米,在它的周围有一条宽1米的环形小路,小路的面积是多少平方米?
20.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=4,ON=1,求⊙O的半径.
21.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
22.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
23.如图,点C在以线段AB为直径的圆上,且,点D在AC上,且DE⊥AB于点E,F是线段BD的中点,连接CE、FE.
(1)若AD=6,BE=8,求EF的长;
(2)求证:CE=EF.
24.已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=BE.
求证:△ADE是等腰三角形.
25.如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为的中点,BF交AD于点E,且BE EF=32,AD=6.
(1)求证:AE=BE;
(2)求DE的长;
(3)求BD的长.
参考答案
一.选择题(共12小题,满分36分)
1.解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
2.解:A、在同圆或等圆中,同一条弦所对的两条弧可能有一条是劣弧,一条是优弧,所以A选项错误;
B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项错误;
C、正多边形一定是轴对称图形,对称轴的条数等于它的边数,所以C选项正确;
D、三角形的外心到三角形三个顶点的距离相等,所以D选项错误.
故选:C.
3.解:连接BE,
∵AE是直径,
∴∠ABE=90°.
∵半径OD⊥弦AB,
∴∠ACO=90°,AC=AB.
∵AB=4,
∴AC=2.
设AO=x,则CO=x﹣1,在Rt△ACO中,由勾股定理,得
x2﹣(x﹣1)2=4,
解得:x=2.5,
∴AE=5.
在Rt△ABE中,由勾股定理,得
BE=3.
在Rt△BCE中,由勾股定理,得
CE=.
故选:B.
4.解:过P作AB⊥OP,交⊙O于A、B,连接OA;
在Rt△OAP中,OA=5,OP=3;
根据勾股定理,得:AP==4;
故AB=2AP=8;
所以过P点的弦长应该在8~10之间,
故选:C.
5.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
6.解:∵车宽2.4米,
∴欲通过如图的隧道,只要比较距隧道中线1.2米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===1.6(m),
CH=CD+DH=1.6+2.5=4.1米,
∴卡车的外形高必须低于4.1米.
故选:A.
7.解:∵=,
∴∠AOB=∠COD=40°,
∴∠BOC=180°﹣40°﹣40°=100°,
∴∠BPC=∠BOC=50°,
故选:B.
8.解:A、直径为弦,所以A选项的说法正确;
B、弦的垂直平分线一定经过圆心,所以B选项的说法正确;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以C选项的说法错误;
D、平分弧的半径垂直于弧所对的弦,所以D选项的说法正确.
故选:C.
9.解:连接OC、OD,
∵AD=CD,
∴=,
∴∠AOD=∠COD,
∵∠AOC=2∠B=2×50°=100°,
∴AOD=50°,
∵OA=OD,
∴∠DAO=∠ADO==65°,即∠DAE=65°,
故选:B.
10.解:连接AC.
∵∠DAB=60°,∠DAC=∠E=42°,
∴∠CAB=60°﹣42°=18°,
∵AB是直径,
∴∠ACB=90°,
∴∠B=90°﹣18°=72°,
故选:C.
11.解:由圆内接四边形的性质可知,∠A+∠C=180°,
∴∠A=180°﹣∠C=70°,
由圆周角定理得,∠BOD=2∠A=140°,
故选:A.
12.解:∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵=,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
故选:C.
二.填空题(共6小题,满分24分)
13.解:(1)∵四边形ABCD为矩形,OC=OD,A(,2),
∴它的中心E点坐标为坐标为(0,1),如图,
∵P1E=1﹣(﹣2)=3,P2E==4,P3E==2
而⊙P的半径为4.
∴矩形ABCD的“等距圆”的圆心是点P2;
(2)设P(t,﹣t+1),
∴PE=4,
∴t2+(﹣t+1﹣1)2=42,解得t=2或t=﹣2,
∴P点坐标为(2,﹣1)或(﹣2,3).
故答案为点P2(2,﹣1)或(﹣2,3).
14.解:根据垂径定理,得AD=AB=20米.
设圆的半径是R,根据勾股定理,
得R2=202+(R﹣10)2,
解得R=25(米),
∴⊙O的直径为50米.
故答案为50.
15.解:连接OA,如图所示,
设直径CD的长为2x寸,则半径OC=x寸,
∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,
∴AE=BE=AB=×10=5寸,
连接OA,则OA=x寸,
根据勾股定理得x2=52+(x﹣1)2,
解得x=13,
CD=2x=2×13=26(寸).
故答案为:26寸.
16.解:连接OC,OD,∵PA=PB,∠P=60°,∴△PAB是等边三角形,
有∠A=∠B=60°,∵OA=OC=OD=OB,∴△COA,△DOB也是等边三角形,
∴∠COA=∠DOB=60°,∴∠COD=180°﹣∠COA﹣∠DOB=60度.
17.解:根据题意,弦AB与两半径组成等边三角形,
∴先AB所对的圆心角=60°,
①圆周角在优弧上时,圆周角=30°,
②圆周角在劣弧上时,圆周角=180°﹣30°=150°.
∴圆周角的度数为30°或150°.
18.解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=β,∠AOC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故答案为:60°.
三.解答题(共7小题,满分60分)
19.解:∵环形小路的宽为1米,花坛的直径为5米,
∴R=3.5m,r=2.5m;
则圆环的面积为:π×(3.5)2﹣π×(2.5)2=6π(平方米),
所以小路的面积为6π平方米.
20.(1)证明:∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,
∴∠AMC=∠AEN=90°,
∵∠ANE=∠CNM,
∴∠BCD=∠BAM,
∴∠BAM=BAD,
在△ANE与△ADE中,
∵,
∴△ANE≌△ADE,
∴AD=AN;
(2)解:∵AB=4,AE⊥CD,
∴AE=2,
又∵ON=1,
∴设NE=x,则OE=x﹣1,NE=ED=x,r=OD=OE+ED=2x﹣1
连接AO,则AO=OD=2x﹣1,
∵△AOE是直角三角形,AE=2,OE=x﹣1,AO=2x﹣1,
∴(2)2+(x﹣1)2=(2x﹣1)2,解得x=2,
∴r=2x﹣1=3.
21.解:这辆卡车能通过厂门.理由如下:
如图M,N为卡车的宽度,过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,
则CD=MN=1.6m,AB=2m,
由作法得,CE=DE=0.8m,
又∵OC=OA=1m,
在Rt△OCE中,OE===0.6(m),
∴CM=2.3+0.6=2.9m>2.5m.
所以这辆卡车能通过厂门.
22.解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∴∠DCO=90°,
∵∠POM=45°,
∴∠CDO=45°,
∴CD=CO,
∴BO=BC+CO=BC+CD,
∴BO=2AB,
连接AO,如图:
∵MN=10,
∴AO=5,
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,
解得:AB=,
则正方形ABCD的边长为.
23.解:(1)∵点C在以线段AB为直径的圆上,且
∴∠ACB=90°,且AC=BC,
∴△ABC为等腰直角三角形,
∴∠A=∠ABC=45°,
∵DE⊥AB,
∴AE=DE=AD=×6=6,
在Rt△BDE中,
∵DE=6,BE=8,
∴BD==10,
又∵F是线段BD的中点,
∴EF=BD=5;
(2)如图,连接CF,
∵∠BED=∠AED=∠ACB=90°,
∵点F是BD的中点,
∴CF=EF=FB=FD,
∴B、C、D、E在以BD为直径的圆上,
∴∠EFC=2∠EBC=2×45°=90°,
∴△EFC为等腰直角三角形,
∴CE=EF.
24.证明:∵A,B,C,D是⊙O上的四点,
∴∠A=∠BCE,
∵BC=BE,
∴∠E=∠BCE,
∴∠A=∠E,
∴DA=DE,即△ADE是等腰三角形.
25.(1)证明:连AF,AB,AC.因为A是的中点,
∴∠ABE=∠AFB.
又∠AFB=∠ACB,
∴∠ABE=∠ACB.
∵BC为直径,
∴∠BAC=90°,AH⊥BC.
∴∠BAE=∠ACB.
∴∠ABE=∠BAE.
∴AE=BE.
(2)解:设DE=x(x>0),由AD=6,BE EF=32,AE EH=BE EF,(4分)
则(6﹣x)(6+x)=32,
解得x=2,
即DE的长为2;
(3)解:由(1)、(2)有:BE=AE=6﹣2=4,
在Rt△BDE中,BD==.
一.选择题(共12小题,满分36分)
1.已知⊙O中最长的弦长8cm,则⊙O的半径是( )
A.2cm B.4cm C.8cm D.16cm
2.下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧 B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形 D.三角形的外心到三角形各边的距离相等
3.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=4,CD=1,则EC的长为( )
A. B. C. D.4
4.如图,⊙O的半径为5,若OP=3,则经过点P的弦长可能是( )
A.3 B.6 C.9 D.12
5.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
6.一辆装满货物,宽为2.4米的卡车,欲通过如图的隧道,则卡车的外形高必须低于( )
A.4.1米 B.4.0米 C.3.9米 D.3.8米
7.如图,AD是⊙O的直径,,若∠AOB=40°,则圆周角∠BPC的度数是( )
A.40° B.50° C.60° D.70°
8.下列语句,错误的是( )
A.直径是弦 B.弦的垂直平分线一定经过圆心
C.相等的圆心角所对的弧相等 D.平分弧的半径垂直于弧所对的弦
9.如图,AE是四边形ABCD外接圆⊙O的直径,AD=CD,∠B=50°,则∠DAE的度数为( )
A.70° B.65° C.60° D.55°
10.如图,AB是⊙O的直径,点C,D在直径AB一侧的圆上(异于A,B两点),点E在直径AB另一侧的圆上,若∠E=42°,∠A=60°,则∠B=( )
A.62° B.70° C.72° D.74°
11.如图,在圆内接四边形ABCD中,∠C=110°,则∠BOD的度数为( )
A.140° B.70° C.80° D.60°
12.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.60° B.55° C.50° D.45°
二.填空题(共6小题,满分24分)
13.对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(,2),顶点C、D在x轴上,OC=OD,且⊙P的半径为4.
(1)在P1(0,﹣2),P2(2,3),P3(﹣2,1)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
(2)如果点P在直线y=x+1上,且⊙P是矩形ABCD的“等距圆”,那么点P的坐标为 .
14.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径= 米.
15.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”.(1尺=10寸)则CD= .
16.如图,已知AB是⊙O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角等于 度.
17.在半径为2的⊙O中,弦AB的长为2,则弦AB所对的圆周角的度数为 .
18.如图,四边形ABCD内接于圆O,四边形ABCO是平行四边形,则∠ADC= .
三.解答题(共7小题,满分60分)
19.一个花坛,直径5米,在它的周围有一条宽1米的环形小路,小路的面积是多少平方米?
20.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=4,ON=1,求⊙O的半径.
21.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
22.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
23.如图,点C在以线段AB为直径的圆上,且,点D在AC上,且DE⊥AB于点E,F是线段BD的中点,连接CE、FE.
(1)若AD=6,BE=8,求EF的长;
(2)求证:CE=EF.
24.已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=BE.
求证:△ADE是等腰三角形.
25.如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为的中点,BF交AD于点E,且BE EF=32,AD=6.
(1)求证:AE=BE;
(2)求DE的长;
(3)求BD的长.
参考答案
一.选择题(共12小题,满分36分)
1.解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
2.解:A、在同圆或等圆中,同一条弦所对的两条弧可能有一条是劣弧,一条是优弧,所以A选项错误;
B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项错误;
C、正多边形一定是轴对称图形,对称轴的条数等于它的边数,所以C选项正确;
D、三角形的外心到三角形三个顶点的距离相等,所以D选项错误.
故选:C.
3.解:连接BE,
∵AE是直径,
∴∠ABE=90°.
∵半径OD⊥弦AB,
∴∠ACO=90°,AC=AB.
∵AB=4,
∴AC=2.
设AO=x,则CO=x﹣1,在Rt△ACO中,由勾股定理,得
x2﹣(x﹣1)2=4,
解得:x=2.5,
∴AE=5.
在Rt△ABE中,由勾股定理,得
BE=3.
在Rt△BCE中,由勾股定理,得
CE=.
故选:B.
4.解:过P作AB⊥OP,交⊙O于A、B,连接OA;
在Rt△OAP中,OA=5,OP=3;
根据勾股定理,得:AP==4;
故AB=2AP=8;
所以过P点的弦长应该在8~10之间,
故选:C.
5.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
6.解:∵车宽2.4米,
∴欲通过如图的隧道,只要比较距隧道中线1.2米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===1.6(m),
CH=CD+DH=1.6+2.5=4.1米,
∴卡车的外形高必须低于4.1米.
故选:A.
7.解:∵=,
∴∠AOB=∠COD=40°,
∴∠BOC=180°﹣40°﹣40°=100°,
∴∠BPC=∠BOC=50°,
故选:B.
8.解:A、直径为弦,所以A选项的说法正确;
B、弦的垂直平分线一定经过圆心,所以B选项的说法正确;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以C选项的说法错误;
D、平分弧的半径垂直于弧所对的弦,所以D选项的说法正确.
故选:C.
9.解:连接OC、OD,
∵AD=CD,
∴=,
∴∠AOD=∠COD,
∵∠AOC=2∠B=2×50°=100°,
∴AOD=50°,
∵OA=OD,
∴∠DAO=∠ADO==65°,即∠DAE=65°,
故选:B.
10.解:连接AC.
∵∠DAB=60°,∠DAC=∠E=42°,
∴∠CAB=60°﹣42°=18°,
∵AB是直径,
∴∠ACB=90°,
∴∠B=90°﹣18°=72°,
故选:C.
11.解:由圆内接四边形的性质可知,∠A+∠C=180°,
∴∠A=180°﹣∠C=70°,
由圆周角定理得,∠BOD=2∠A=140°,
故选:A.
12.解:∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵=,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
故选:C.
二.填空题(共6小题,满分24分)
13.解:(1)∵四边形ABCD为矩形,OC=OD,A(,2),
∴它的中心E点坐标为坐标为(0,1),如图,
∵P1E=1﹣(﹣2)=3,P2E==4,P3E==2
而⊙P的半径为4.
∴矩形ABCD的“等距圆”的圆心是点P2;
(2)设P(t,﹣t+1),
∴PE=4,
∴t2+(﹣t+1﹣1)2=42,解得t=2或t=﹣2,
∴P点坐标为(2,﹣1)或(﹣2,3).
故答案为点P2(2,﹣1)或(﹣2,3).
14.解:根据垂径定理,得AD=AB=20米.
设圆的半径是R,根据勾股定理,
得R2=202+(R﹣10)2,
解得R=25(米),
∴⊙O的直径为50米.
故答案为50.
15.解:连接OA,如图所示,
设直径CD的长为2x寸,则半径OC=x寸,
∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,
∴AE=BE=AB=×10=5寸,
连接OA,则OA=x寸,
根据勾股定理得x2=52+(x﹣1)2,
解得x=13,
CD=2x=2×13=26(寸).
故答案为:26寸.
16.解:连接OC,OD,∵PA=PB,∠P=60°,∴△PAB是等边三角形,
有∠A=∠B=60°,∵OA=OC=OD=OB,∴△COA,△DOB也是等边三角形,
∴∠COA=∠DOB=60°,∴∠COD=180°﹣∠COA﹣∠DOB=60度.
17.解:根据题意,弦AB与两半径组成等边三角形,
∴先AB所对的圆心角=60°,
①圆周角在优弧上时,圆周角=30°,
②圆周角在劣弧上时,圆周角=180°﹣30°=150°.
∴圆周角的度数为30°或150°.
18.解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=β,∠AOC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故答案为:60°.
三.解答题(共7小题,满分60分)
19.解:∵环形小路的宽为1米,花坛的直径为5米,
∴R=3.5m,r=2.5m;
则圆环的面积为:π×(3.5)2﹣π×(2.5)2=6π(平方米),
所以小路的面积为6π平方米.
20.(1)证明:∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,
∴∠AMC=∠AEN=90°,
∵∠ANE=∠CNM,
∴∠BCD=∠BAM,
∴∠BAM=BAD,
在△ANE与△ADE中,
∵,
∴△ANE≌△ADE,
∴AD=AN;
(2)解:∵AB=4,AE⊥CD,
∴AE=2,
又∵ON=1,
∴设NE=x,则OE=x﹣1,NE=ED=x,r=OD=OE+ED=2x﹣1
连接AO,则AO=OD=2x﹣1,
∵△AOE是直角三角形,AE=2,OE=x﹣1,AO=2x﹣1,
∴(2)2+(x﹣1)2=(2x﹣1)2,解得x=2,
∴r=2x﹣1=3.
21.解:这辆卡车能通过厂门.理由如下:
如图M,N为卡车的宽度,过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,
则CD=MN=1.6m,AB=2m,
由作法得,CE=DE=0.8m,
又∵OC=OA=1m,
在Rt△OCE中,OE===0.6(m),
∴CM=2.3+0.6=2.9m>2.5m.
所以这辆卡车能通过厂门.
22.解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∴∠DCO=90°,
∵∠POM=45°,
∴∠CDO=45°,
∴CD=CO,
∴BO=BC+CO=BC+CD,
∴BO=2AB,
连接AO,如图:
∵MN=10,
∴AO=5,
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,
解得:AB=,
则正方形ABCD的边长为.
23.解:(1)∵点C在以线段AB为直径的圆上,且
∴∠ACB=90°,且AC=BC,
∴△ABC为等腰直角三角形,
∴∠A=∠ABC=45°,
∵DE⊥AB,
∴AE=DE=AD=×6=6,
在Rt△BDE中,
∵DE=6,BE=8,
∴BD==10,
又∵F是线段BD的中点,
∴EF=BD=5;
(2)如图,连接CF,
∵∠BED=∠AED=∠ACB=90°,
∵点F是BD的中点,
∴CF=EF=FB=FD,
∴B、C、D、E在以BD为直径的圆上,
∴∠EFC=2∠EBC=2×45°=90°,
∴△EFC为等腰直角三角形,
∴CE=EF.
24.证明:∵A,B,C,D是⊙O上的四点,
∴∠A=∠BCE,
∵BC=BE,
∴∠E=∠BCE,
∴∠A=∠E,
∴DA=DE,即△ADE是等腰三角形.
25.(1)证明:连AF,AB,AC.因为A是的中点,
∴∠ABE=∠AFB.
又∠AFB=∠ACB,
∴∠ABE=∠ACB.
∵BC为直径,
∴∠BAC=90°,AH⊥BC.
∴∠BAE=∠ACB.
∴∠ABE=∠BAE.
∴AE=BE.
(2)解:设DE=x(x>0),由AD=6,BE EF=32,AE EH=BE EF,(4分)
则(6﹣x)(6+x)=32,
解得x=2,
即DE的长为2;
(3)解:由(1)、(2)有:BE=AE=6﹣2=4,
在Rt△BDE中,BD==.
同课章节目录
