1.3.2函数的奇偶性
图片预览



文档简介
(共18张PPT)
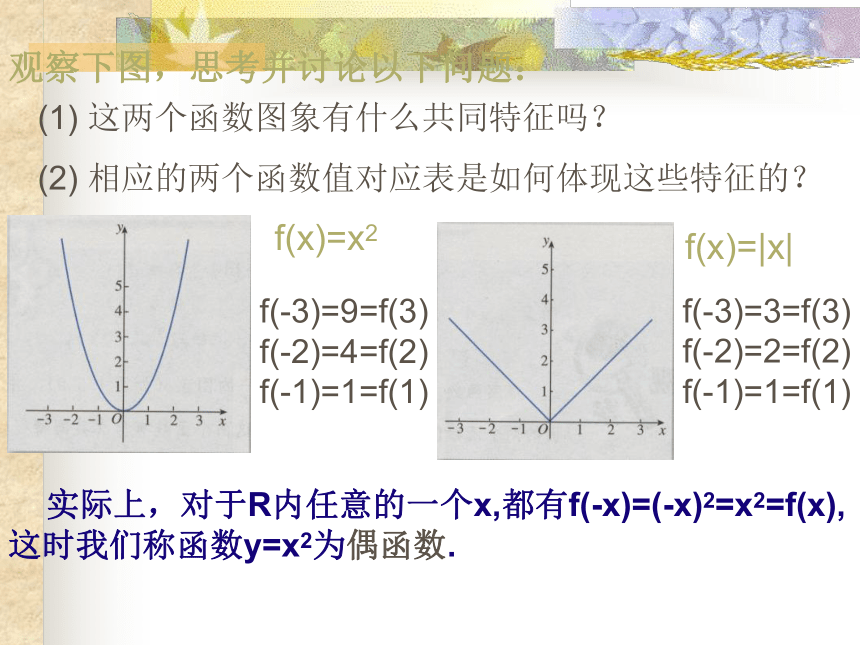
观察下图,思考并讨论以下问题:
(1) 这两个函数图象有什么共同特征吗?
(2) 相应的两个函数值对应表是如何体现这些特征的?
f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)
f(-3)=3=f(3) f(-2)=2=f(2) f(-1)=1=f(1)
f(x)=x2
f(x)=|x|
实际上,对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.
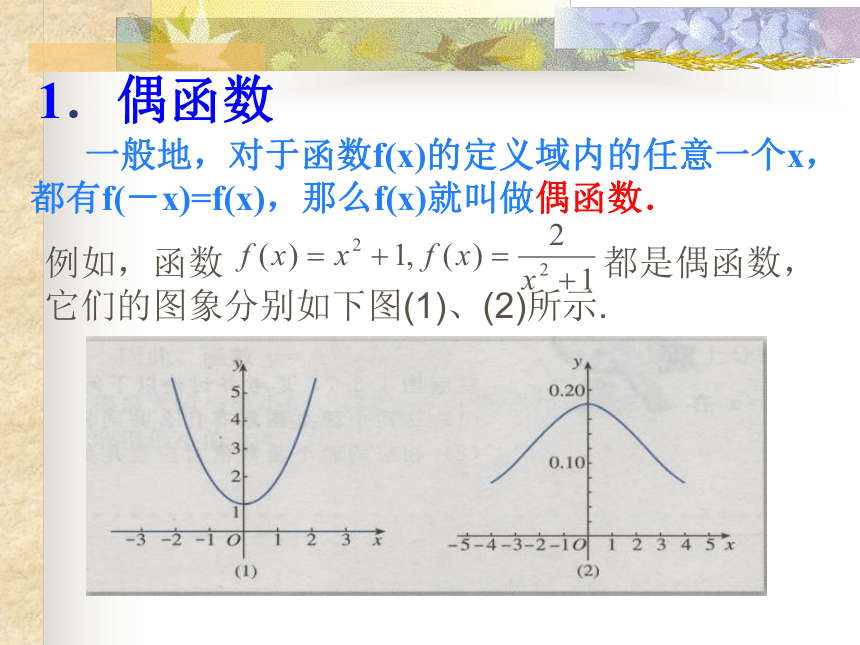
1.偶函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
例如,函数 都是偶函数,它们的图象分别如下图(1)、(2)所示.
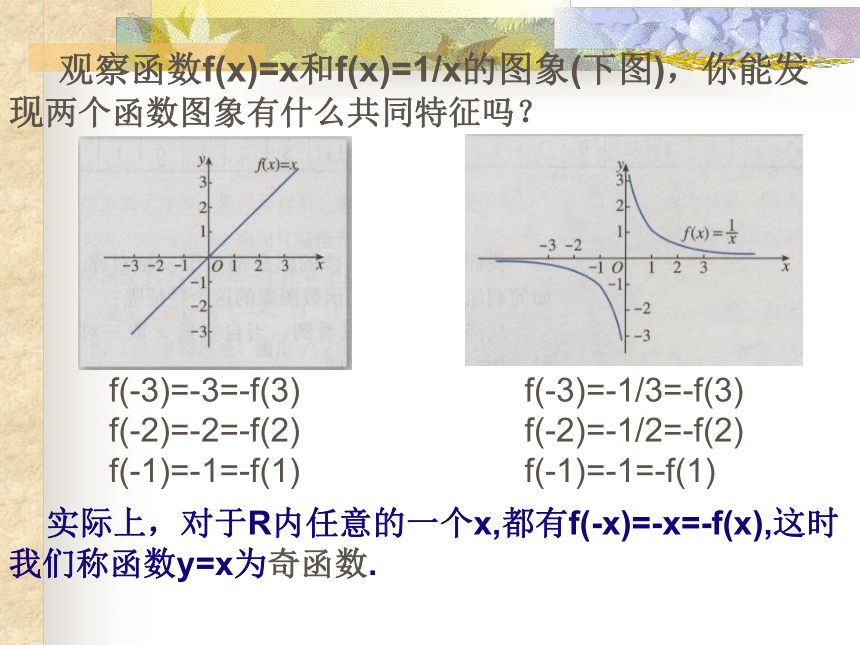
观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?
f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)
实际上,对于R内任意的一个x,都有f(-x)=-x=-f(x),这时我们称函数y=x为奇函数.
f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)
2.奇函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)= - f(x),那么f(x)就叫做奇函数.
注意:
1、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
2、由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
3、奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立.
4、如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.
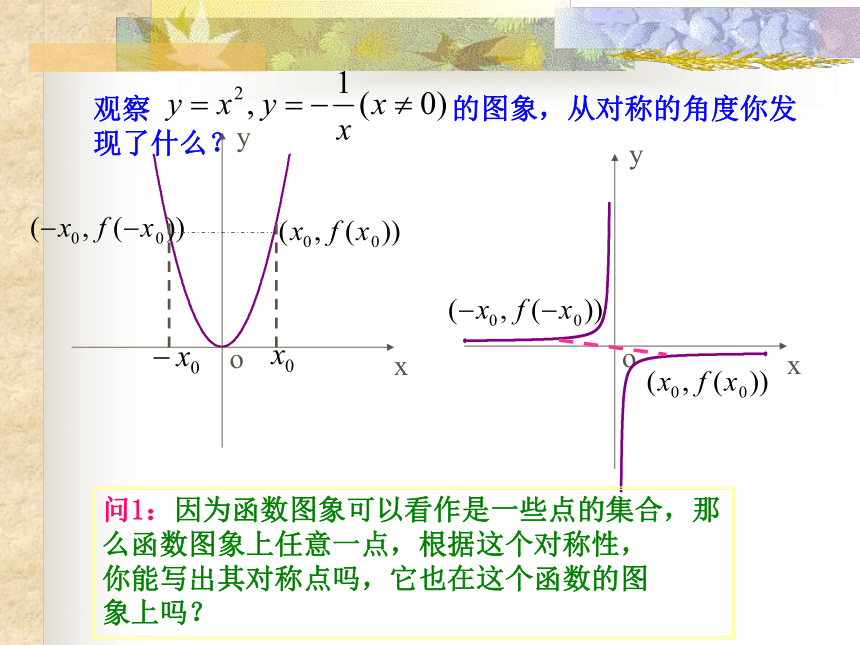
观察 的图象,从对称的角度你发
现了什么?
x
y
o
x
y
o
问1:因为函数图象可以看作是一些点的集合,那
么函数图象上任意一点,根据这个对称性,
你能写出其对称点吗,它也在这个函数的图
象上吗?
关于y轴对称
关于原点对称
问2:怎样用数量关系来表示 和其对称
呢?
若 和 关于y轴对称,则有
若 和 关于原点对称,则有
定义法证明函数奇偶性的步骤:
(1)写出函数的定义域,并判断是否关于原点对称
(2)考察f(x)与f(-x)的关系
问3:函数具有奇偶性,其定义域必须具有怎样的特点?
判断函数奇偶性的方法:
(1)定义法 数
(2)图象法 形
例5、判断下列函数的奇偶性:
(1)解:定义域为R ∵ f(-x)=(-x)4=f(x)
即f(-x)=f(x)
∴f(x)偶函数
(2)解:定义域为R f(-x)=(-x)5=- x5 =-f(x)
即f(-x)=-f(x)
∴f(x)奇函数
(3)解:定义域为{x|x≠0} ∵ f(-x)=-x+1/(-x)=-f(x)
即f(-x)=-f(x)
∴f(x)奇函数
(4)解:定义域为{x|x≠0} ∵ f(-x)=1/(-x)2=f(x)
即f(-x)=f(x)
∴f(x)偶函数
例6:判定下列函数是否为偶函数或奇函数
解 (4)函数 的定义域为R
所以函数 既不是奇函数也不是
偶函数
补例:偶函数f(x)在 是增函数,试比较
的大小?
例7 判断函数
是否具有奇偶性
3.用定义判断函数奇偶性的步骤:
(1)、先求定义域,看是否关于原点对称;
(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.
课堂练习
判断下列函数的奇偶性:
3.奇偶函数图象的性质
1、奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.
2、偶函数的图象关于y轴对称. 反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.
说明:奇偶函数图象的性质可用于:
a、简化函数图象的画法. B、判断函数的奇偶性
本课小结
1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数
2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
2、已知函数 是偶函数,求实数m的值
课后作业
1、判断下列函数的奇偶性
3、已知定义在R上的偶函数f(x)在区间 上是增函
数,若 ,求x的取值范围
观察下图,思考并讨论以下问题:
(1) 这两个函数图象有什么共同特征吗?
(2) 相应的两个函数值对应表是如何体现这些特征的?
f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)
f(-3)=3=f(3) f(-2)=2=f(2) f(-1)=1=f(1)
f(x)=x2
f(x)=|x|
实际上,对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.
1.偶函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
例如,函数 都是偶函数,它们的图象分别如下图(1)、(2)所示.
观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?
f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)
实际上,对于R内任意的一个x,都有f(-x)=-x=-f(x),这时我们称函数y=x为奇函数.
f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)
2.奇函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)= - f(x),那么f(x)就叫做奇函数.
注意:
1、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
2、由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
3、奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立.
4、如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.
观察 的图象,从对称的角度你发
现了什么?
x
y
o
x
y
o
问1:因为函数图象可以看作是一些点的集合,那
么函数图象上任意一点,根据这个对称性,
你能写出其对称点吗,它也在这个函数的图
象上吗?
关于y轴对称
关于原点对称
问2:怎样用数量关系来表示 和其对称
呢?
若 和 关于y轴对称,则有
若 和 关于原点对称,则有
定义法证明函数奇偶性的步骤:
(1)写出函数的定义域,并判断是否关于原点对称
(2)考察f(x)与f(-x)的关系
问3:函数具有奇偶性,其定义域必须具有怎样的特点?
判断函数奇偶性的方法:
(1)定义法 数
(2)图象法 形
例5、判断下列函数的奇偶性:
(1)解:定义域为R ∵ f(-x)=(-x)4=f(x)
即f(-x)=f(x)
∴f(x)偶函数
(2)解:定义域为R f(-x)=(-x)5=- x5 =-f(x)
即f(-x)=-f(x)
∴f(x)奇函数
(3)解:定义域为{x|x≠0} ∵ f(-x)=-x+1/(-x)=-f(x)
即f(-x)=-f(x)
∴f(x)奇函数
(4)解:定义域为{x|x≠0} ∵ f(-x)=1/(-x)2=f(x)
即f(-x)=f(x)
∴f(x)偶函数
例6:判定下列函数是否为偶函数或奇函数
解 (4)函数 的定义域为R
所以函数 既不是奇函数也不是
偶函数
补例:偶函数f(x)在 是增函数,试比较
的大小?
例7 判断函数
是否具有奇偶性
3.用定义判断函数奇偶性的步骤:
(1)、先求定义域,看是否关于原点对称;
(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.
课堂练习
判断下列函数的奇偶性:
3.奇偶函数图象的性质
1、奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.
2、偶函数的图象关于y轴对称. 反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.
说明:奇偶函数图象的性质可用于:
a、简化函数图象的画法. B、判断函数的奇偶性
本课小结
1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数
2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
2、已知函数 是偶函数,求实数m的值
课后作业
1、判断下列函数的奇偶性
3、已知定义在R上的偶函数f(x)在区间 上是增函
数,若 ,求x的取值范围
