2021-2022学年度人教版七年级数学上册 2.1 整 式(3课时)(教案)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学上册 2.1 整 式(3课时)(教案) |  | |
| 格式 | doc | ||
| 文件大小 | 166.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 14:29:43 | ||
图片预览



文档简介
2.1 整 式
第1课时 用字母表示数
一、基本目标
【知识与技能】
1.使学生理解用字母表示数的意义.
2.掌握用字母表示数量关系的方法和技巧.
【过程与方法】
在探索现实世界数量关系的过程中,建立符号意识,初步体会数学中的抽象思维.
【情感态度与价值观】
1.让学生体会用字母表示数的优越性.
2.培养严谨、认真、理论联系实际的科学态度与学风.
二、重难点目标
【教学重点】
理解用字母表示数的意义.
【教学难点】
用含有字母的式子表示实际问题中的数量关系.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P54~P55的内容,完成下面练习.
【3 min反馈】
1.用字母表示:
(1)有理数减法法则:a-b=a+(-b);
(2)有理数除法法则:a÷b=a·(b≠0).
2.客车每小时行v千米,t小时行的路程为vt千米.
3.一本名著有a页,王红读了b天,还剩c页未读,王红平均每天读了页.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )
A.(1-10%)(1+15%)x万元
B.(1-10%+15%)x万元
C.(x-10%)(x+15%)万元
D.(1+10%-15%)x万元
【互动探索】(引发学生思考)根据题意可得,2月份的产值是(1-10%)x万元,则3月份的产值是(1-10%)(1+15%)x万元.
【答案】A
【互动总结】(学生总结,老师点评)列代数式时,要抓住语句中的关键词语的意义,如和、差、积、商、比、倍、分、大、小、增加了、增加到、减少、几倍、几分之几等.
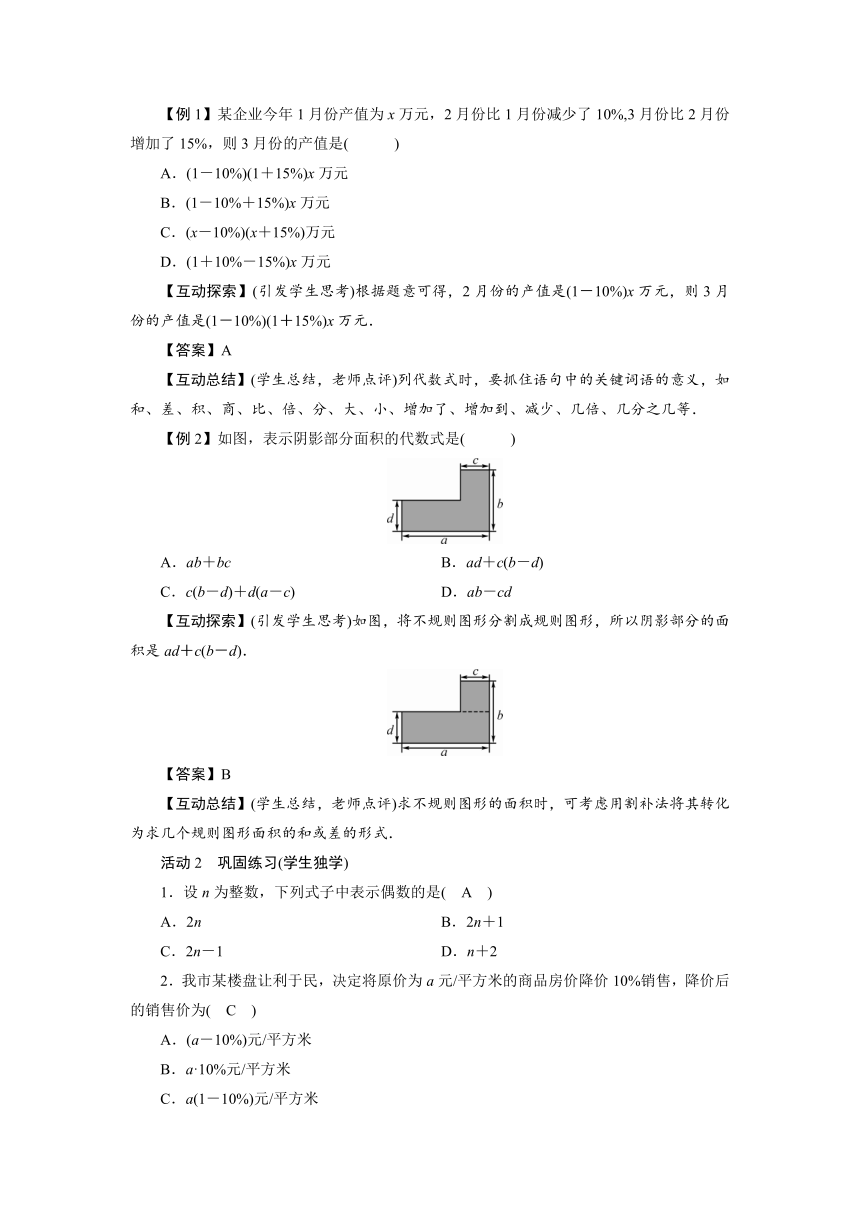
【例2】如图,表示阴影部分面积的代数式是( )
A.ab+bc B.ad+c(b-d)
C.c(b-d)+d(a-c) D.ab-cd
【互动探索】(引发学生思考)如图,将不规则图形分割成规则图形,所以阴影部分的面积是ad+c(b-d).
【答案】B
【互动总结】(学生总结,老师点评)求不规则图形的面积时,可考虑用割补法将其转化为求几个规则图形面积的和或差的形式.
活动2 巩固练习(学生独学)
1.设n为整数,下列式子中表示偶数的是( A )
A.2n B.2n+1
C.2n-1 D.n+2
2.我市某楼盘让利于民,决定将原价为a元/平方米的商品房价降价10%销售,降价后的销售价为( C )
A.(a-10%)元/平方米
B.a·10%元/平方米
C.a(1-10%)元/平方米
D.a(1+10%)元/平方米
3.如果手机通话每分钟收费m元,那么通话n分钟收费mn元.
4.用代数式表示:
(1)a与3的和的2倍;
(2)a、b的平方的和;
(3)n与1的和除以n与a的差;
(4)某厂1月份产量为a吨,以后每个月比上一个月增产x%,求该厂3月份的产量.
解:(1)2(a+3).
(2)a2+b2.
(3).
(4)a(1+x%)2吨.
活动3 拓展延伸(学生对学)
【例3】如图是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有________根小棒.
【互动探索】由图可知,第1个图案中有5+1=6(根)小棒;第2个图案中有2×5+1=11(根)小棒;第3个图案中有3×5+1=16(根)小棒;…;由此得出第n个图案中有5n+1根小棒.
【答案】5n+1
【互动总结】(学生总结,老师点评)要先观察图形,找出图形之间的联系,得出规律,利用规律解决问题.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
用字母表示数
请完成本课时对应练习!
第2课时 单项式
一、基本目标
【知识与技能】
使学生理解单项式及单项式的系数、次数的概念,并能找出单项式的系数、次数.
【过程与方法】
初步学会观察、对比、归纳的方法;发展学生的观察能力、思维能力及分析能力.
【情感态度与价值观】
在平等的教学氛围中,通过学生之间、师生之间的交流、合作与评价,拉近学生之间、师生之间的情感距离.
二、重难点目标
【教学重点】
掌握单项式及单项式的系数、次数的概念.
【教学难点】
能正确识别单项式的系数、次数.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P56~P57的内容,完成下面练习.
【3 min反馈】
1.由数与字母或字母与字母相乘组成的代数式叫做单项式.
2.单项式中的数字因数叫做这个单项式的系数.
3.单项式中所有字母的指数的和叫做单项式的次数.
4.在式子1,a2,a-b,y,x,中,是单项式的有1,a2,y,x.
5.(1)-a的系数是-1,次数是1;
(2)单项式-3x2的系数是-3,次数是2;
(3)的系数是,次数是5.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】用单项式填空,并指出它们的系数和次数.
(1)每包书有12册,n包书有________册;
(2)底边长为a cm,高为h cm的三角形的面积是________ cm2;
(3)棱长为a cm的正方体的体积是________ cm3;
(4)一台电视机原价b元,现按原价的9折出售,这台电视机现在的售价是________元;
(5)一个长方形的长是0.9 m,宽是b m,这个长方形的面积是________m2.
【解答】见教材第57页例3.
【教师点拨】用字母表示数后,同一个式子可以表示不同的含义.
【例2】的系数与次数分别为( )
A.,7 B.,6
C.4π,6 D.,4
【互动探索】(引发学生思考)单项式中系数是什么?怎样求单项式的次数呢?
的系数为,次数为6.
【答案】B
【互动总结】(学生总结,老师点评)注意π是一个常数,不是字母.
活动2 巩固练习(学生独学)
1.下列各式中,次数为3的单项式是( B )
A.x3+y3 B.x2y
C.x3y D.3xy
2.下列代数式中,属于单项式的是( D )
A.a+1 B.a2-b
C. D.
3.填表:
单项式 2a2 -1.2h 3xy2 -2t2 -0.3vt
系数
次数
解:如下表:
单项式 2a2 -1.2h 3xy2 -2t2 -0.3vt
系数 2 -1.2 3 -2 -0.3
次数 2 1 3 2 2
4.若关于x、y的单项式2xym与-ax2y2的系数、次数相同,试求a、m的值.
解:因为关于x、y的单项式2xym与-ax2y2系数、次数相同,
所以-a=2,1+m=4,
解得a=-2,m=3.
活动3 拓展延伸(学生对学)
【例3】观察下列各式:
-a,a2,-a3,a4,-a5,a6,…
(1)写出第2017个和2018个单项式;
(2)写出第n个单项式.
【互动探索】由-a,a2,-a3,a4,-a5,a6,…可得第n项的表达式为(-1)n.将2017和2018分别代入表达式即可得解.
【解答】(1)第2017个单项式为-,第2018个单项式为.
(2)第n个单项式为(-1)n.
【互动总结】(学生总结,老师点评)本题主要考查了单项式,解题的关键是求出单项式的排列规律.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
单项式
请完成本课时对应练习!
第3课时 多项式
一、基本目标
【知识与技能】
1.掌握多项式、整式的概念.
2.能熟练说出多项式的项数和次数.
【过程与方法】
通过观察、讨论、自主探究等形式,发展学生的抽象概括能力.
【情感态度与价值观】
培养学生积极思考的学习态度,合作交流意识,了解整式的实际背景,进一步感受字母表示数的意义.
二、重难点目标
【教学重点】
多项式的概念及多项式的项数、次数的概念.
【教学难点】
多项式的次数.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P57~P58的内容,完成下面练习.
【3 min反馈】
1.几个单项式的和叫做多项式,每个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数,不含字母的项叫做多项式的常数项.
2.单项式和多项式统称为整式.
3.多项式3a3-中,常数项是( D )
A.1 B.-1
C. D.-
4.多项式3x2y-4xy-1由单项式3x2y,-4xy,-1组成,它是三次三项式,其中二次项是-4xy,常数项是-1.
5.多项式-m2n2+m3-2n-3是四次四项式,最高次项的系数为-1,常数项是-3.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】指出下列多项式的项和次数:
(1)a3-a2b+ab2-b3;
(2)3n4-2n2+1.
【互动探索】(引发学生思考)什么是多项式的项?什么是多项式的次数?
【解答】(1)多项式的项:a3,-a2b,ab2,-b3,多项式的次数是3.
(2)多项式的项:3n4,-2n2,1,多项式的次数是4.
【互动总结】(学生总结,老师点评)此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项.多项式里,次数最高项的次数,叫做多项式的次数.
【例2】下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
,,,2x+y,-2xy2,,ab,π,-2x+y2,.
【互动探索】(引发学生思考)多项式与单项式的区别在哪里?单项式都属于整式吗?多项式呢?
【解答】整式有:,2x+y,-2xy2,ab,π,-2x+y2,.
单项式有:,-2xy2,ab,π.
多项式有:2x+y,-2x+y2,.
【互动总结】(学生总结,老师点评)既不是单项式,也不是多项式的代数式,一定不是整式.
活动2 巩固练习(学生独学)
1.已知多项式4x3-3x2+x-5,下列说法错误的是( B )
A.三次项的系数是4
B.二次项的系数是3
C.一次项的系数是1
D.常数项是-5
2.下列说法中正确的有( A )
①单项式-πx2y的系数是-;
②多项式a+3b+ab是一次多项式;
③多项式3a2b3-4ab+2的第二项是4ab;
④2x2+-3是多项式.
A.0个 B.1个
C.2个 D.3个
3.下列各式中是整式的是①②③④⑤⑥⑦⑧,是多项式的是③⑥,是单项式的是①②④⑤⑦⑧.(填序号)
①0;②x2;③-x2-2x+5;④;⑤xy;⑥8+;⑦-5;⑧.
4.指出下列多项式的项和次数.
(1)x3-x+1;
(2)3x3-2x2y2+3y2.
解:(1)多项式的项:x3,-x,1,多项式的次数是3.
(2)多项式的项:3x3,-2x2y2,3y2,多项式的次数是4.
活动3 拓展延伸(学生对学)
【例3】已知多项式xm+1y2+2xy2-4x3+1是六次四项式,单项式26x2ny5-m的次数与该多项式的次数相同,求(-m)3+2n的值.
【互动探索】利用多项式与单项式的次数与系数的确定方法得出关于m与n的方程进而得出答案.
【解答】因为多项式是六次四项式,
所以m+1+2=6,解得m=3.
故单项式26x2ny5-m=26x2ny2,
所以2n+2=6,解得n=2.
故(-m)3+2n=(-3)3+2×2=-23.
【互动总结】(学生总结,老师点评)利用多项式、单项式的次数的定义,正确得出待定的字母的取值后,代入代数式求值即可.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
整式
请完成本课时对应练习!
第1课时 用字母表示数
一、基本目标
【知识与技能】
1.使学生理解用字母表示数的意义.
2.掌握用字母表示数量关系的方法和技巧.
【过程与方法】
在探索现实世界数量关系的过程中,建立符号意识,初步体会数学中的抽象思维.
【情感态度与价值观】
1.让学生体会用字母表示数的优越性.
2.培养严谨、认真、理论联系实际的科学态度与学风.
二、重难点目标
【教学重点】
理解用字母表示数的意义.
【教学难点】
用含有字母的式子表示实际问题中的数量关系.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P54~P55的内容,完成下面练习.
【3 min反馈】
1.用字母表示:
(1)有理数减法法则:a-b=a+(-b);
(2)有理数除法法则:a÷b=a·(b≠0).
2.客车每小时行v千米,t小时行的路程为vt千米.
3.一本名著有a页,王红读了b天,还剩c页未读,王红平均每天读了页.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )
A.(1-10%)(1+15%)x万元
B.(1-10%+15%)x万元
C.(x-10%)(x+15%)万元
D.(1+10%-15%)x万元
【互动探索】(引发学生思考)根据题意可得,2月份的产值是(1-10%)x万元,则3月份的产值是(1-10%)(1+15%)x万元.
【答案】A
【互动总结】(学生总结,老师点评)列代数式时,要抓住语句中的关键词语的意义,如和、差、积、商、比、倍、分、大、小、增加了、增加到、减少、几倍、几分之几等.
【例2】如图,表示阴影部分面积的代数式是( )
A.ab+bc B.ad+c(b-d)
C.c(b-d)+d(a-c) D.ab-cd
【互动探索】(引发学生思考)如图,将不规则图形分割成规则图形,所以阴影部分的面积是ad+c(b-d).
【答案】B
【互动总结】(学生总结,老师点评)求不规则图形的面积时,可考虑用割补法将其转化为求几个规则图形面积的和或差的形式.
活动2 巩固练习(学生独学)
1.设n为整数,下列式子中表示偶数的是( A )
A.2n B.2n+1
C.2n-1 D.n+2
2.我市某楼盘让利于民,决定将原价为a元/平方米的商品房价降价10%销售,降价后的销售价为( C )
A.(a-10%)元/平方米
B.a·10%元/平方米
C.a(1-10%)元/平方米
D.a(1+10%)元/平方米
3.如果手机通话每分钟收费m元,那么通话n分钟收费mn元.
4.用代数式表示:
(1)a与3的和的2倍;
(2)a、b的平方的和;
(3)n与1的和除以n与a的差;
(4)某厂1月份产量为a吨,以后每个月比上一个月增产x%,求该厂3月份的产量.
解:(1)2(a+3).
(2)a2+b2.
(3).
(4)a(1+x%)2吨.
活动3 拓展延伸(学生对学)
【例3】如图是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有________根小棒.
【互动探索】由图可知,第1个图案中有5+1=6(根)小棒;第2个图案中有2×5+1=11(根)小棒;第3个图案中有3×5+1=16(根)小棒;…;由此得出第n个图案中有5n+1根小棒.
【答案】5n+1
【互动总结】(学生总结,老师点评)要先观察图形,找出图形之间的联系,得出规律,利用规律解决问题.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
用字母表示数
请完成本课时对应练习!
第2课时 单项式
一、基本目标
【知识与技能】
使学生理解单项式及单项式的系数、次数的概念,并能找出单项式的系数、次数.
【过程与方法】
初步学会观察、对比、归纳的方法;发展学生的观察能力、思维能力及分析能力.
【情感态度与价值观】
在平等的教学氛围中,通过学生之间、师生之间的交流、合作与评价,拉近学生之间、师生之间的情感距离.
二、重难点目标
【教学重点】
掌握单项式及单项式的系数、次数的概念.
【教学难点】
能正确识别单项式的系数、次数.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P56~P57的内容,完成下面练习.
【3 min反馈】
1.由数与字母或字母与字母相乘组成的代数式叫做单项式.
2.单项式中的数字因数叫做这个单项式的系数.
3.单项式中所有字母的指数的和叫做单项式的次数.
4.在式子1,a2,a-b,y,x,中,是单项式的有1,a2,y,x.
5.(1)-a的系数是-1,次数是1;
(2)单项式-3x2的系数是-3,次数是2;
(3)的系数是,次数是5.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】用单项式填空,并指出它们的系数和次数.
(1)每包书有12册,n包书有________册;
(2)底边长为a cm,高为h cm的三角形的面积是________ cm2;
(3)棱长为a cm的正方体的体积是________ cm3;
(4)一台电视机原价b元,现按原价的9折出售,这台电视机现在的售价是________元;
(5)一个长方形的长是0.9 m,宽是b m,这个长方形的面积是________m2.
【解答】见教材第57页例3.
【教师点拨】用字母表示数后,同一个式子可以表示不同的含义.
【例2】的系数与次数分别为( )
A.,7 B.,6
C.4π,6 D.,4
【互动探索】(引发学生思考)单项式中系数是什么?怎样求单项式的次数呢?
的系数为,次数为6.
【答案】B
【互动总结】(学生总结,老师点评)注意π是一个常数,不是字母.
活动2 巩固练习(学生独学)
1.下列各式中,次数为3的单项式是( B )
A.x3+y3 B.x2y
C.x3y D.3xy
2.下列代数式中,属于单项式的是( D )
A.a+1 B.a2-b
C. D.
3.填表:
单项式 2a2 -1.2h 3xy2 -2t2 -0.3vt
系数
次数
解:如下表:
单项式 2a2 -1.2h 3xy2 -2t2 -0.3vt
系数 2 -1.2 3 -2 -0.3
次数 2 1 3 2 2
4.若关于x、y的单项式2xym与-ax2y2的系数、次数相同,试求a、m的值.
解:因为关于x、y的单项式2xym与-ax2y2系数、次数相同,
所以-a=2,1+m=4,
解得a=-2,m=3.
活动3 拓展延伸(学生对学)
【例3】观察下列各式:
-a,a2,-a3,a4,-a5,a6,…
(1)写出第2017个和2018个单项式;
(2)写出第n个单项式.
【互动探索】由-a,a2,-a3,a4,-a5,a6,…可得第n项的表达式为(-1)n.将2017和2018分别代入表达式即可得解.
【解答】(1)第2017个单项式为-,第2018个单项式为.
(2)第n个单项式为(-1)n.
【互动总结】(学生总结,老师点评)本题主要考查了单项式,解题的关键是求出单项式的排列规律.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
单项式
请完成本课时对应练习!
第3课时 多项式
一、基本目标
【知识与技能】
1.掌握多项式、整式的概念.
2.能熟练说出多项式的项数和次数.
【过程与方法】
通过观察、讨论、自主探究等形式,发展学生的抽象概括能力.
【情感态度与价值观】
培养学生积极思考的学习态度,合作交流意识,了解整式的实际背景,进一步感受字母表示数的意义.
二、重难点目标
【教学重点】
多项式的概念及多项式的项数、次数的概念.
【教学难点】
多项式的次数.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P57~P58的内容,完成下面练习.
【3 min反馈】
1.几个单项式的和叫做多项式,每个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数,不含字母的项叫做多项式的常数项.
2.单项式和多项式统称为整式.
3.多项式3a3-中,常数项是( D )
A.1 B.-1
C. D.-
4.多项式3x2y-4xy-1由单项式3x2y,-4xy,-1组成,它是三次三项式,其中二次项是-4xy,常数项是-1.
5.多项式-m2n2+m3-2n-3是四次四项式,最高次项的系数为-1,常数项是-3.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】指出下列多项式的项和次数:
(1)a3-a2b+ab2-b3;
(2)3n4-2n2+1.
【互动探索】(引发学生思考)什么是多项式的项?什么是多项式的次数?
【解答】(1)多项式的项:a3,-a2b,ab2,-b3,多项式的次数是3.
(2)多项式的项:3n4,-2n2,1,多项式的次数是4.
【互动总结】(学生总结,老师点评)此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项.多项式里,次数最高项的次数,叫做多项式的次数.
【例2】下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
,,,2x+y,-2xy2,,ab,π,-2x+y2,.
【互动探索】(引发学生思考)多项式与单项式的区别在哪里?单项式都属于整式吗?多项式呢?
【解答】整式有:,2x+y,-2xy2,ab,π,-2x+y2,.
单项式有:,-2xy2,ab,π.
多项式有:2x+y,-2x+y2,.
【互动总结】(学生总结,老师点评)既不是单项式,也不是多项式的代数式,一定不是整式.
活动2 巩固练习(学生独学)
1.已知多项式4x3-3x2+x-5,下列说法错误的是( B )
A.三次项的系数是4
B.二次项的系数是3
C.一次项的系数是1
D.常数项是-5
2.下列说法中正确的有( A )
①单项式-πx2y的系数是-;
②多项式a+3b+ab是一次多项式;
③多项式3a2b3-4ab+2的第二项是4ab;
④2x2+-3是多项式.
A.0个 B.1个
C.2个 D.3个
3.下列各式中是整式的是①②③④⑤⑥⑦⑧,是多项式的是③⑥,是单项式的是①②④⑤⑦⑧.(填序号)
①0;②x2;③-x2-2x+5;④;⑤xy;⑥8+;⑦-5;⑧.
4.指出下列多项式的项和次数.
(1)x3-x+1;
(2)3x3-2x2y2+3y2.
解:(1)多项式的项:x3,-x,1,多项式的次数是3.
(2)多项式的项:3x3,-2x2y2,3y2,多项式的次数是4.
活动3 拓展延伸(学生对学)
【例3】已知多项式xm+1y2+2xy2-4x3+1是六次四项式,单项式26x2ny5-m的次数与该多项式的次数相同,求(-m)3+2n的值.
【互动探索】利用多项式与单项式的次数与系数的确定方法得出关于m与n的方程进而得出答案.
【解答】因为多项式是六次四项式,
所以m+1+2=6,解得m=3.
故单项式26x2ny5-m=26x2ny2,
所以2n+2=6,解得n=2.
故(-m)3+2n=(-3)3+2×2=-23.
【互动总结】(学生总结,老师点评)利用多项式、单项式的次数的定义,正确得出待定的字母的取值后,代入代数式求值即可.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
整式
请完成本课时对应练习!
