2021-2022学年度人教版七年级数学上册教案 4.1几何图形(含3课时)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学上册教案 4.1几何图形(含3课时) |  | |
| 格式 | doc | ||
| 文件大小 | 623.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 10:11:13 | ||
图片预览


文档简介
4.1 几何图形
4.1.1 立体图形与平面图形
第1课时 认识几何图形
一、基本目标
【知识与技能】
1.通过实物和具体模型,了解从物体外形抽象出来的几何体、平面、直线和点的概念.
2.初步了解立体图形和平面图形的概念.
【过程与方法】
经历从实物中抽象出几何图形的过程,体会空间构成.
【情感态度与价值观】
激发学生对“空间与图形”的探究欲望,唤起学生爱生活、爱数学的热情.
二、重难点目标
【教学重点】
识别一些基本几何体.
【教学难点】
理解从物体外形抽象出的几何体、平面、直线和点的概念.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P114~P116的内容,完成下面练习.
【3 min反馈】
1.对于各种各样的物体,数学关注的是它们的形状、大小、位置关系.
2.几何图形:如长方体、圆柱、球、正方形、圆等.从实物中抽象出的图形统称几何图形.
3.立体图形:如长方体、正方体、圆柱、圆锥、球等几何图形的各部分不都在同一平面内,它们是立体图形.
4.平面图形:长方形、正方形、三角形、圆、线段等几何图形的各部分都在同一平面内,它们是平面图形.
5.立体图形某些部分是平面图形,例如长方体的侧面是长方形.
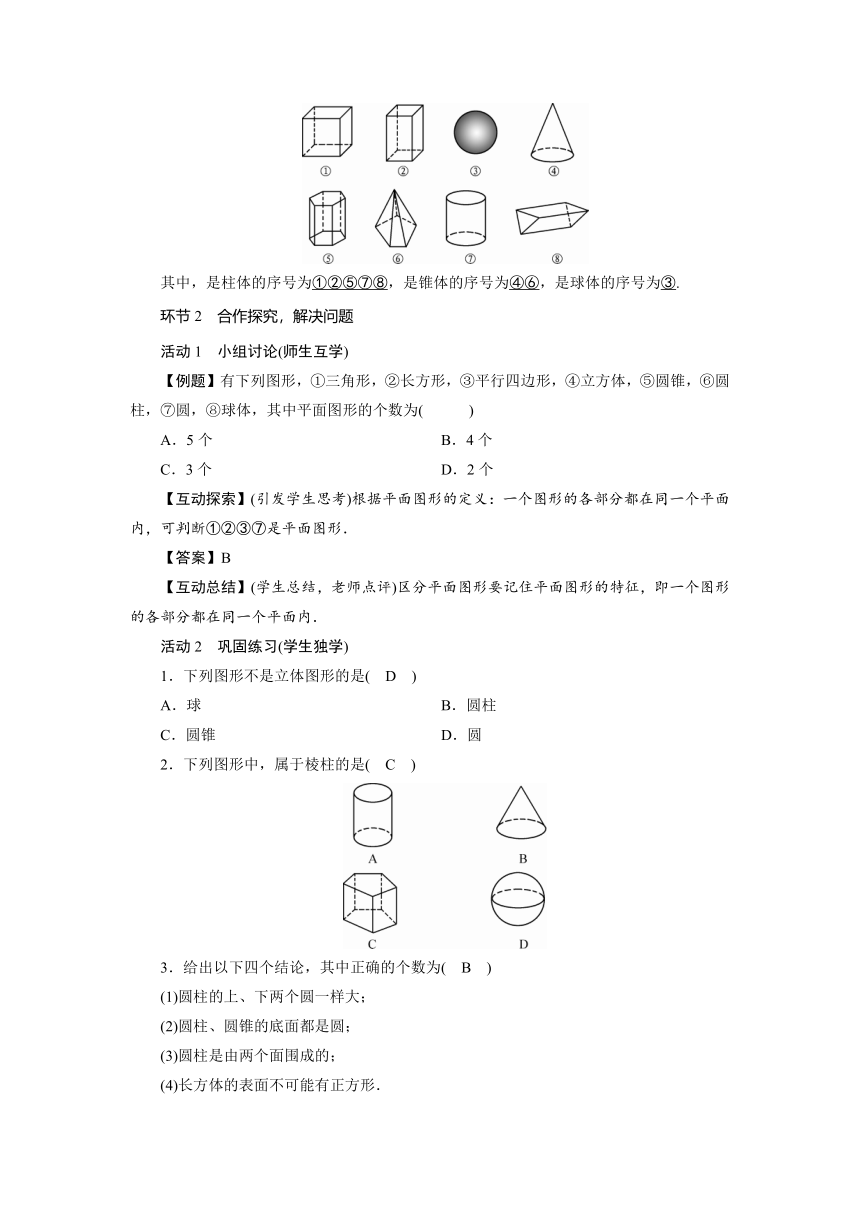
6.如图所示为8个立体图形.
其中,是柱体的序号为①②⑤⑦⑧,是锥体的序号为④⑥,是球体的序号为③.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例题】有下列图形,①三角形,②长方形,③平行四边形,④立方体,⑤圆锥,⑥圆柱,⑦圆,⑧球体,其中平面图形的个数为( )
A.5个 B.4个
C.3个 D.2个
【互动探索】(引发学生思考)根据平面图形的定义:一个图形的各部分都在同一个平面内,可判断①②③⑦是平面图形.
【答案】B
【互动总结】(学生总结,老师点评)区分平面图形要记住平面图形的特征,即一个图形的各部分都在同一个平面内.
活动2 巩固练习(学生独学)
1.下列图形不是立体图形的是( D )
A.球 B.圆柱
C.圆锥 D.圆
2.下列图形中,属于棱柱的是( C )
3.给出以下四个结论,其中正确的个数为( B )
(1)圆柱的上、下两个圆一样大;
(2)圆柱、圆锥的底面都是圆;
(3)圆柱是由两个面围成的;
(4)长方体的表面不可能有正方形.
A.1个 B.2个
C.3个 D.4个
4.与如图相对应的几何图形的名称为( D )
A.四棱锥 B.三棱锥
C.四棱柱 D.三棱柱
环节3 课堂小结,当堂达标
(学生总结,老师点评)
几何图形
请完成本课时对应练习!
第2课时 折叠与展开
一、基本目标
【知识与技能】
1.能从不同角度观察一些几何体,以及它们的组合体,并画出平面图形.
2.了解一些立体图形的表面展开图.
3.能根据展开图想象相应的几何体.
【过程与方法】
认识可以用平面图形表示立体图形,以及立体图形与平面图形的联系.
【情感态度与价值观】
培养学生对学习几何图形的兴趣,激发学生热爱生活的情感.
二、重难点目标
【教学重点】
了解一些简单立体图形的展开图.
【教学难点】
根据展开图想象几何体.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P117~P118的内容,完成下面练习.
【3 min反馈】
1.有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的展开图.
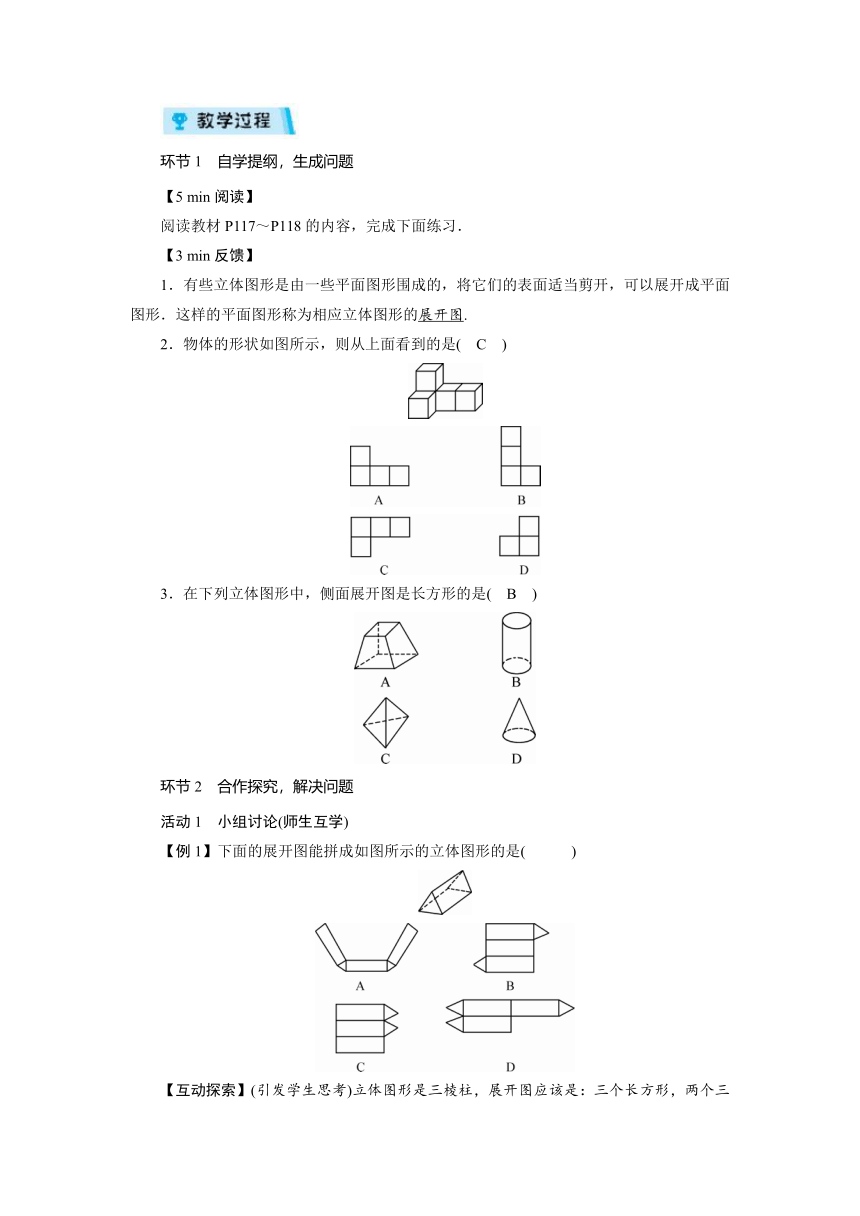
2.物体的形状如图所示,则从上面看到的是( C )
3.在下列立体图形中,侧面展开图是长方形的是( B )
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】下面的展开图能拼成如图所示的立体图形的是( )
【互动探索】(引发学生思考)立体图形是三棱柱,展开图应该是:三个长方形,两个三角形,两个三角形位于三个长方形两侧;A选项折叠后两个长方形重合,故排除;C、D选项折叠后三角形都在一侧,故排除.
【答案】B
【互动总结】(学生总结,老师点评)此题主要考查了展开图折叠成几何体.通过立体图形与平面图形的相互转化,理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
活动2 巩固练习(学生独学)
1.一个几何体从正面、左面、上面看得到的图形如图所示,那么这个几何体是下列选项中的( D )
2.指出下面的三个图形分别是上面这个物体从哪个方向看到的图形.
3.如图为一个多面体的表面展开图,每个面内都标注了数字.若数字为1的面是底面,则朝上一面所标注的数字为( B )
A.5 B.4
C.3 D.2
活动3 拓展延伸(学生对学)
【例2】过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图为( )
【互动探索】选项A、C、D折叠后都不符合题意,只有选项B折叠后两个剪去的三角形与另一个剪去的三角形交于一个顶点,与正方体三个剪去的三角形交于一个顶点符合.
【答案】B
【互动总结】(学生总结,老师点评)本题考查几何体的展开图.解决此类问题,要充分考虑带有各种符号的面的特点及位置.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
1.从不同的方向观察立体图形
(1)判断从不同的方向看到的图形
(2)根据从不同的方向看到的图形判断几何体
2.立体图形的展开图
(1)几何体的展开图
(2)由展开图判断几何体
请完成本课时对应练习!
4.1.2 点、线、面、体(第3课时)
一、基本目标
【知识与技能】
了解点、线、面、体之间的关系.
【过程与方法】
培养学生操作、观察、分析、猜测和概括等能力,同时渗透转化、化归、变换等思想.
【情感态度与价值观】
使学生养成积极主动的学习态度和自主学习的方式.
二、重难点目标
【教学重点】
认识点、线、面、体的几何特征,感受它们之间的关系.
【教学难点】
理解点动成线、线动成面、面动成体的联系.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P119~P121的内容,完成下面练习.
【3 min反馈】
1.几何体简称体,包围着体的是面,面分为平面和曲面.
2.面与面相交的地方成线.线有直线和曲线.线与线相交的地方是点.
3.几何图形都是由点、线、面、体组成的,其中点是基本元素.
4.笔尖在纸上快速滑动写出了一个又一个字,这说明了点动成线;车轮旋转时,车轮上的辐条会形成一个整体的圆面,这说明了线动成面;直角三角形绕它的直角边旋转一周,形成了一个圆锥体,这说明了面动成体.
5.如图,各图中的阴影图形绕着直线l旋转360°,各自能形成怎样的立体图形?
解:圆柱,圆锥,球.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
【互动探索】(引发学生思考)由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
【答案】D
【互动总结】(学生总结,老师点评)此题考查了点、线、面、体,重在体现面动成体,需要发挥立体图形的空间想象能力及提高分析问题、解决问题的能力.
活动2 巩固练习(学生独学)
1.如图,圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,下列选项中四个平面图形绕着直线旋转一周可以得到该图的是( A )
2.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的4个图案中,符合图示滚涂出的图案是( A )
3.如图所示,正方形ABCD的边长为3 cm,以边AB所在直线为轴,将正方形旋转一周,所得几何体从正面看得到的图形的面积是18 cm2.
活动3 拓展延伸(学生对学)
【例2】已知柱体的体积V=S·h,其中S表示柱体的底面面积,h表示柱体的高.现将矩形ABCD绕轴l旋转一周,则形成的几何体的体积等于( )
A.πr2h B.2πr2h
C.3πr2h D.4πr2h
【互动探索】现将矩形ABCD绕轴l旋转一周,柱体的底面圆环面积为π(2r)2-πr2=3πr2,形成的几何体的体积等于3πr2h.
【答案】C
【互动总结】(学生总结,老师点评)先判断旋转后的立体图形的形状,然后利用相应的计算公式进行解答.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
体由面组成,面与面相交成线,线与线相交成点.
点的形成:线与线相交成点,点无大小.
线的形成线无粗细
面的形成:线动成面
体的形成
请完成本课时对应练习!
4.1.1 立体图形与平面图形
第1课时 认识几何图形
一、基本目标
【知识与技能】
1.通过实物和具体模型,了解从物体外形抽象出来的几何体、平面、直线和点的概念.
2.初步了解立体图形和平面图形的概念.
【过程与方法】
经历从实物中抽象出几何图形的过程,体会空间构成.
【情感态度与价值观】
激发学生对“空间与图形”的探究欲望,唤起学生爱生活、爱数学的热情.
二、重难点目标
【教学重点】
识别一些基本几何体.
【教学难点】
理解从物体外形抽象出的几何体、平面、直线和点的概念.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P114~P116的内容,完成下面练习.
【3 min反馈】
1.对于各种各样的物体,数学关注的是它们的形状、大小、位置关系.
2.几何图形:如长方体、圆柱、球、正方形、圆等.从实物中抽象出的图形统称几何图形.
3.立体图形:如长方体、正方体、圆柱、圆锥、球等几何图形的各部分不都在同一平面内,它们是立体图形.
4.平面图形:长方形、正方形、三角形、圆、线段等几何图形的各部分都在同一平面内,它们是平面图形.
5.立体图形某些部分是平面图形,例如长方体的侧面是长方形.
6.如图所示为8个立体图形.
其中,是柱体的序号为①②⑤⑦⑧,是锥体的序号为④⑥,是球体的序号为③.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例题】有下列图形,①三角形,②长方形,③平行四边形,④立方体,⑤圆锥,⑥圆柱,⑦圆,⑧球体,其中平面图形的个数为( )
A.5个 B.4个
C.3个 D.2个
【互动探索】(引发学生思考)根据平面图形的定义:一个图形的各部分都在同一个平面内,可判断①②③⑦是平面图形.
【答案】B
【互动总结】(学生总结,老师点评)区分平面图形要记住平面图形的特征,即一个图形的各部分都在同一个平面内.
活动2 巩固练习(学生独学)
1.下列图形不是立体图形的是( D )
A.球 B.圆柱
C.圆锥 D.圆
2.下列图形中,属于棱柱的是( C )
3.给出以下四个结论,其中正确的个数为( B )
(1)圆柱的上、下两个圆一样大;
(2)圆柱、圆锥的底面都是圆;
(3)圆柱是由两个面围成的;
(4)长方体的表面不可能有正方形.
A.1个 B.2个
C.3个 D.4个
4.与如图相对应的几何图形的名称为( D )
A.四棱锥 B.三棱锥
C.四棱柱 D.三棱柱
环节3 课堂小结,当堂达标
(学生总结,老师点评)
几何图形
请完成本课时对应练习!
第2课时 折叠与展开
一、基本目标
【知识与技能】
1.能从不同角度观察一些几何体,以及它们的组合体,并画出平面图形.
2.了解一些立体图形的表面展开图.
3.能根据展开图想象相应的几何体.
【过程与方法】
认识可以用平面图形表示立体图形,以及立体图形与平面图形的联系.
【情感态度与价值观】
培养学生对学习几何图形的兴趣,激发学生热爱生活的情感.
二、重难点目标
【教学重点】
了解一些简单立体图形的展开图.
【教学难点】
根据展开图想象几何体.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P117~P118的内容,完成下面练习.
【3 min反馈】
1.有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的展开图.
2.物体的形状如图所示,则从上面看到的是( C )
3.在下列立体图形中,侧面展开图是长方形的是( B )
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】下面的展开图能拼成如图所示的立体图形的是( )
【互动探索】(引发学生思考)立体图形是三棱柱,展开图应该是:三个长方形,两个三角形,两个三角形位于三个长方形两侧;A选项折叠后两个长方形重合,故排除;C、D选项折叠后三角形都在一侧,故排除.
【答案】B
【互动总结】(学生总结,老师点评)此题主要考查了展开图折叠成几何体.通过立体图形与平面图形的相互转化,理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
活动2 巩固练习(学生独学)
1.一个几何体从正面、左面、上面看得到的图形如图所示,那么这个几何体是下列选项中的( D )
2.指出下面的三个图形分别是上面这个物体从哪个方向看到的图形.
3.如图为一个多面体的表面展开图,每个面内都标注了数字.若数字为1的面是底面,则朝上一面所标注的数字为( B )
A.5 B.4
C.3 D.2
活动3 拓展延伸(学生对学)
【例2】过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图为( )
【互动探索】选项A、C、D折叠后都不符合题意,只有选项B折叠后两个剪去的三角形与另一个剪去的三角形交于一个顶点,与正方体三个剪去的三角形交于一个顶点符合.
【答案】B
【互动总结】(学生总结,老师点评)本题考查几何体的展开图.解决此类问题,要充分考虑带有各种符号的面的特点及位置.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
1.从不同的方向观察立体图形
(1)判断从不同的方向看到的图形
(2)根据从不同的方向看到的图形判断几何体
2.立体图形的展开图
(1)几何体的展开图
(2)由展开图判断几何体
请完成本课时对应练习!
4.1.2 点、线、面、体(第3课时)
一、基本目标
【知识与技能】
了解点、线、面、体之间的关系.
【过程与方法】
培养学生操作、观察、分析、猜测和概括等能力,同时渗透转化、化归、变换等思想.
【情感态度与价值观】
使学生养成积极主动的学习态度和自主学习的方式.
二、重难点目标
【教学重点】
认识点、线、面、体的几何特征,感受它们之间的关系.
【教学难点】
理解点动成线、线动成面、面动成体的联系.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P119~P121的内容,完成下面练习.
【3 min反馈】
1.几何体简称体,包围着体的是面,面分为平面和曲面.
2.面与面相交的地方成线.线有直线和曲线.线与线相交的地方是点.
3.几何图形都是由点、线、面、体组成的,其中点是基本元素.
4.笔尖在纸上快速滑动写出了一个又一个字,这说明了点动成线;车轮旋转时,车轮上的辐条会形成一个整体的圆面,这说明了线动成面;直角三角形绕它的直角边旋转一周,形成了一个圆锥体,这说明了面动成体.
5.如图,各图中的阴影图形绕着直线l旋转360°,各自能形成怎样的立体图形?
解:圆柱,圆锥,球.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
【互动探索】(引发学生思考)由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
【答案】D
【互动总结】(学生总结,老师点评)此题考查了点、线、面、体,重在体现面动成体,需要发挥立体图形的空间想象能力及提高分析问题、解决问题的能力.
活动2 巩固练习(学生独学)
1.如图,圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,下列选项中四个平面图形绕着直线旋转一周可以得到该图的是( A )
2.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的4个图案中,符合图示滚涂出的图案是( A )
3.如图所示,正方形ABCD的边长为3 cm,以边AB所在直线为轴,将正方形旋转一周,所得几何体从正面看得到的图形的面积是18 cm2.
活动3 拓展延伸(学生对学)
【例2】已知柱体的体积V=S·h,其中S表示柱体的底面面积,h表示柱体的高.现将矩形ABCD绕轴l旋转一周,则形成的几何体的体积等于( )
A.πr2h B.2πr2h
C.3πr2h D.4πr2h
【互动探索】现将矩形ABCD绕轴l旋转一周,柱体的底面圆环面积为π(2r)2-πr2=3πr2,形成的几何体的体积等于3πr2h.
【答案】C
【互动总结】(学生总结,老师点评)先判断旋转后的立体图形的形状,然后利用相应的计算公式进行解答.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
体由面组成,面与面相交成线,线与线相交成点.
点的形成:线与线相交成点,点无大小.
线的形成线无粗细
面的形成:线动成面
体的形成
请完成本课时对应练习!
