2021-2022学年度人教版七年级数学上册教案 4.4课题学习 设计制作长方体形状的包装纸盒
文档属性
| 名称 | 2021-2022学年度人教版七年级数学上册教案 4.4课题学习 设计制作长方体形状的包装纸盒 | 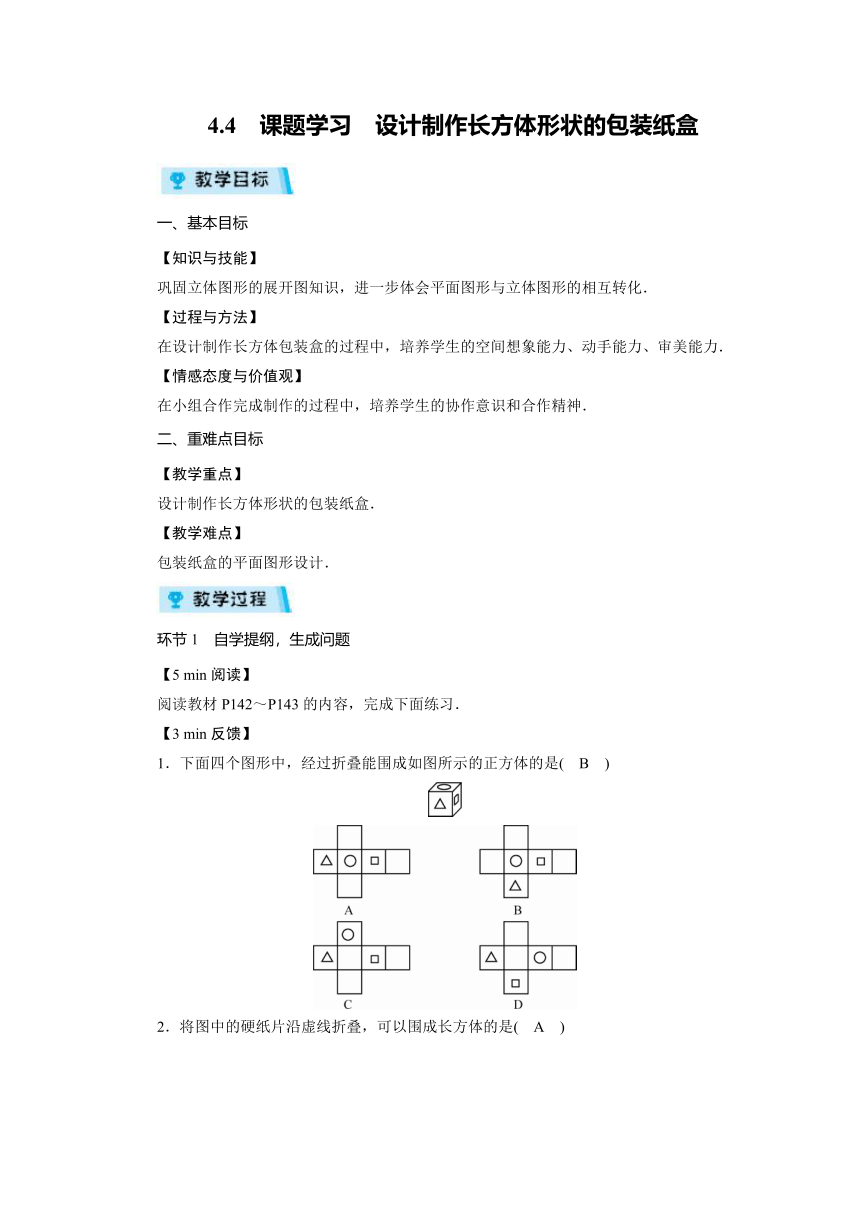 | |
| 格式 | doc | ||
| 文件大小 | 307.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 10:12:35 | ||
图片预览

文档简介
4.4 课题学习 设计制作长方体形状的包装纸盒
一、基本目标
【知识与技能】
巩固立体图形的展开图知识,进一步体会平面图形与立体图形的相互转化.
【过程与方法】
在设计制作长方体包装盒的过程中,培养学生的空间想象能力、动手能力、审美能力.
【情感态度与价值观】
在小组合作完成制作的过程中,培养学生的协作意识和合作精神.
二、重难点目标
【教学重点】
设计制作长方体形状的包装纸盒.
【教学难点】
包装纸盒的平面图形设计.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P142~P143的内容,完成下面练习.
【3 min反馈】
1.下面四个图形中,经过折叠能围成如图所示的正方体的是( B )
2.将图中的硬纸片沿虚线折叠,可以围成长方体的是( A )
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
1.按照教材P142~143的活动过程设计一个长方体形状的包装盒.
【教师点拨】(1)设计各种各样的长(正)方体形状包装盒时,要先绘制长(正)方体的表面展开图,再把它剪出并折叠成长(正)方体,此外,还要用到美术知识、语言知识、生产知识等.
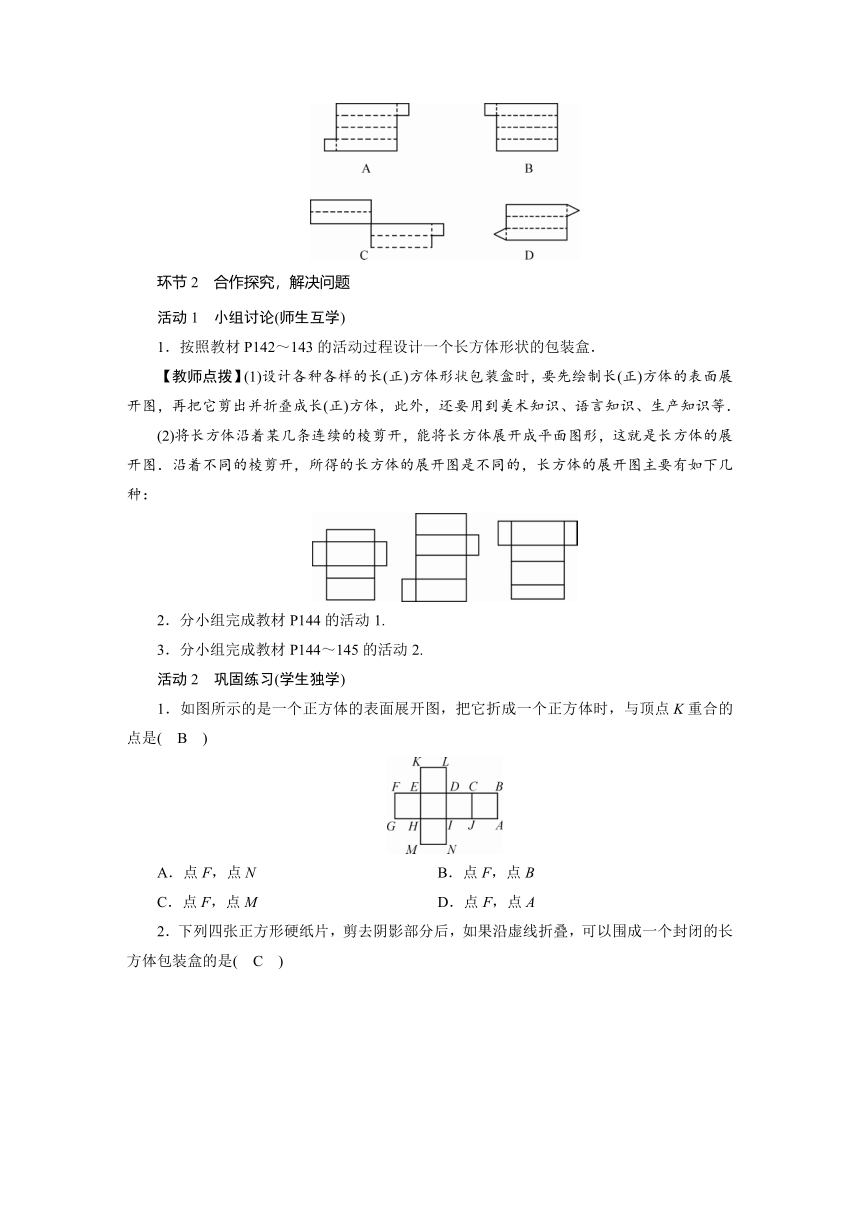
(2)将长方体沿着某几条连续的棱剪开,能将长方体展开成平面图形,这就是长方体的展开图.沿着不同的棱剪开,所得的长方体的展开图是不同的,长方体的展开图主要有如下几种:
2.分小组完成教材P144的活动1.
3.分小组完成教材P144~145的活动2.
活动2 巩固练习(学生独学)
1.如图所示的是一个正方体的表面展开图,把它折成一个正方体时,与顶点K重合的点是( B )
A.点F,点N B.点F,点B
C.点F,点M D.点F,点A
2.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( C )
3.下列图形中,可以沿虚线折叠成长方体包装盒的有(1)(3).
4.有两个正方体,它们的表面上画有形状和排列彼此完全相同的图案,如图1和图2所示的分别是这两个正方体表面的展开图,请你在图2的4个空白方格中补上应有的图案.
解:如图所示.
活动3 拓展延伸(学生对学)
【例题】某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如图所示,其中阴影部分为内部粘贴角料.(单位:毫米)
(1)此长方体包装盒的体积为________立方毫米;(用含x、y的式子表示)
(2)此长方体的表面积(不含内部粘贴角料)为________平方毫米;(用含x、y的式子表示)
(3)若内部粘贴角料的面积占长方体表面纸板面积的,求当x=40毫米,y=70毫米时,制作这样一个长方体共需要纸板多少平方毫米.
【互动探索】(1)由长方体包装盒的平面展开图,可知该长方体的长为y毫米,宽为x毫米,高为65毫米,根据长方体的体积=长×宽×高即可求解;
(2)根据长方形的面积公式即可得出结论;
(3)由于长方体的表面积=2(长×宽+长×高+宽×高),又内部粘贴角料的面积占长方体表面纸板面积的,所以制作这样一个长方体共需要纸板的面积=(1+)×长方体的表面积.
【解答】(1)65xy
(2)2(xy+65y+65x)
(3)因为长方体的长为y毫米,宽为x毫米,高为65毫米,
所以长方体的表面积=2(xy+65y+65x)平方毫米.
又因为内部粘贴角料的面积占长方体表面纸板面积的,
所以制作这样一个长方体共需要纸板的面积=(1+)×2(xy+65y+65x)=(xy+65y+65x)=xy+156y+156x(平方毫米).
因为x=40,y=70,
所以制作这样一个长方体共需要纸板×40×70+156×70+156×40=23880(平方毫米).
【互动总结】(学生总结,老师点评)本题考查了长方体的平面展开图,长方体的体积与表面积公式,解题关键是掌握立体图形与平面展开图之间的关系,从图中得到长方体的长、宽、高.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
设计各种各样的长(正)方体形状包装盒时,要先绘制长(正)方体的表面展开图,再把它剪出并折叠成长(正)方体,此外,还要用到美术知识、语言知识、生产知识等.
请完成本课时对应练习!
一、基本目标
【知识与技能】
巩固立体图形的展开图知识,进一步体会平面图形与立体图形的相互转化.
【过程与方法】
在设计制作长方体包装盒的过程中,培养学生的空间想象能力、动手能力、审美能力.
【情感态度与价值观】
在小组合作完成制作的过程中,培养学生的协作意识和合作精神.
二、重难点目标
【教学重点】
设计制作长方体形状的包装纸盒.
【教学难点】
包装纸盒的平面图形设计.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P142~P143的内容,完成下面练习.
【3 min反馈】
1.下面四个图形中,经过折叠能围成如图所示的正方体的是( B )
2.将图中的硬纸片沿虚线折叠,可以围成长方体的是( A )
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
1.按照教材P142~143的活动过程设计一个长方体形状的包装盒.
【教师点拨】(1)设计各种各样的长(正)方体形状包装盒时,要先绘制长(正)方体的表面展开图,再把它剪出并折叠成长(正)方体,此外,还要用到美术知识、语言知识、生产知识等.
(2)将长方体沿着某几条连续的棱剪开,能将长方体展开成平面图形,这就是长方体的展开图.沿着不同的棱剪开,所得的长方体的展开图是不同的,长方体的展开图主要有如下几种:
2.分小组完成教材P144的活动1.
3.分小组完成教材P144~145的活动2.
活动2 巩固练习(学生独学)
1.如图所示的是一个正方体的表面展开图,把它折成一个正方体时,与顶点K重合的点是( B )
A.点F,点N B.点F,点B
C.点F,点M D.点F,点A
2.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( C )
3.下列图形中,可以沿虚线折叠成长方体包装盒的有(1)(3).
4.有两个正方体,它们的表面上画有形状和排列彼此完全相同的图案,如图1和图2所示的分别是这两个正方体表面的展开图,请你在图2的4个空白方格中补上应有的图案.
解:如图所示.
活动3 拓展延伸(学生对学)
【例题】某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如图所示,其中阴影部分为内部粘贴角料.(单位:毫米)
(1)此长方体包装盒的体积为________立方毫米;(用含x、y的式子表示)
(2)此长方体的表面积(不含内部粘贴角料)为________平方毫米;(用含x、y的式子表示)
(3)若内部粘贴角料的面积占长方体表面纸板面积的,求当x=40毫米,y=70毫米时,制作这样一个长方体共需要纸板多少平方毫米.
【互动探索】(1)由长方体包装盒的平面展开图,可知该长方体的长为y毫米,宽为x毫米,高为65毫米,根据长方体的体积=长×宽×高即可求解;
(2)根据长方形的面积公式即可得出结论;
(3)由于长方体的表面积=2(长×宽+长×高+宽×高),又内部粘贴角料的面积占长方体表面纸板面积的,所以制作这样一个长方体共需要纸板的面积=(1+)×长方体的表面积.
【解答】(1)65xy
(2)2(xy+65y+65x)
(3)因为长方体的长为y毫米,宽为x毫米,高为65毫米,
所以长方体的表面积=2(xy+65y+65x)平方毫米.
又因为内部粘贴角料的面积占长方体表面纸板面积的,
所以制作这样一个长方体共需要纸板的面积=(1+)×2(xy+65y+65x)=(xy+65y+65x)=xy+156y+156x(平方毫米).
因为x=40,y=70,
所以制作这样一个长方体共需要纸板×40×70+156×70+156×40=23880(平方毫米).
【互动总结】(学生总结,老师点评)本题考查了长方体的平面展开图,长方体的体积与表面积公式,解题关键是掌握立体图形与平面展开图之间的关系,从图中得到长方体的长、宽、高.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
设计各种各样的长(正)方体形状包装盒时,要先绘制长(正)方体的表面展开图,再把它剪出并折叠成长(正)方体,此外,还要用到美术知识、语言知识、生产知识等.
请完成本课时对应练习!
