第一章 基本的几何图形导学案
图片预览



文档简介
第一章 基本的几何图形
1.1我们身边的图形世界学案
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1.能说出一些常见的几何体、平面图形。
2.能识别生活中的几何体
3.能识别优美图案中的平面图形。
二、自主预习
1.如果对于我们看到的物体,只研究它们的 、 、 ,
而不考虑 、 、 等其他性质时,就得到各种几何体,几何体简称 。
2.镜面、黑板面、操场、平静的水面等都给我们以 的形象。数学上所说的平面是从所有具备这种形象的事物中抽象出来的,平面没有厚薄,没有边界,是向四面八方 。
3.生活中,除了平面的形象外,还有 的形象。
4.体是由 围成的。
三、导学探究
1.几何体
(1).独立看书第4页-第5页,观察与思考,尽可能的完成书上提出的有关问题和练习。(对于出现的疑难问题,可采用学生交流讨论)
(2)几何体简称 ,我们只研究他们的 、 、 。
(3)举出一些你熟悉的几何体,至少5个。
。
2.面
(1)生活中,我们见到很多平面的例子,请举出一些。
(2)生活中,除了平面的形象外,你还会经常见到曲的面的形象。请举出一些。
3.体和面的关系
是由 围成的。请举出一些例子。(小组之间可以交流)
4.练习
(1)、独立完成课本上的练习1-2
(2)、完成习题1.1,并与同学交流。
四、当堂达标
1.找出生活中与下列几何体形状类似的物体各一个.
(1)正方体:_______ (2)圆柱 :_______
(4)长方体 :_______ (5) 圆锥:_______ (6)球 :_______
2.由生活中的物体抽象出几何图形,在后面的横线上填出对应的几何体.
收音机_______ 杯子_______ 砖块_______
纸箱_______ 足球_______ 易拉罐_______ 粉笔盒_______
堆沙子_______ 魔方_______
3.判断下列的陈述是否正确:
(1)圆柱、圆锥的底面都是圆( )
(2)圆柱的侧面是平面( )
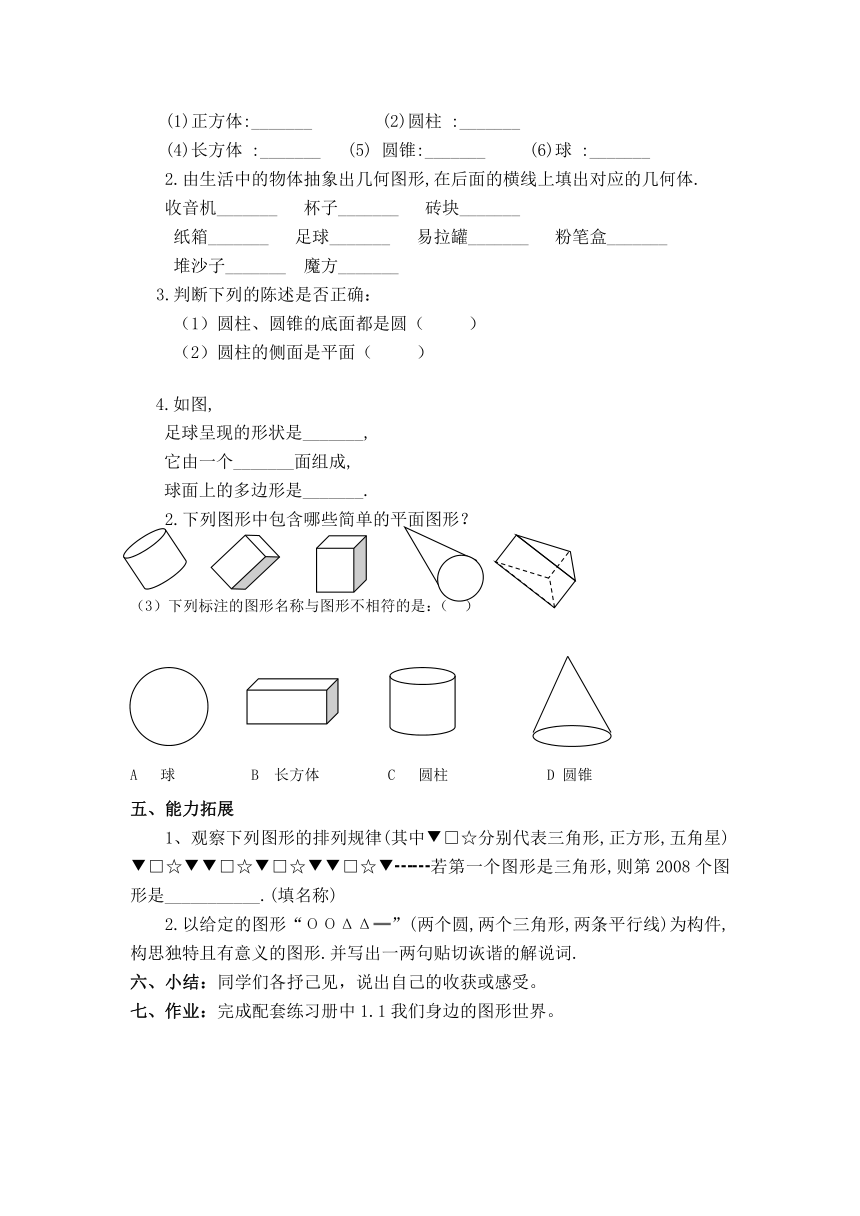
4.如图,
足球呈现的形状是_______,
它由一个_______面组成,
球面上的多边形是_______.
2.下列图形中包含哪些简单的平面图形?
(3)下列标注的图形名称与图形不相符的是:( )
A 球 B 长方体 C 圆柱 D 圆锥
五、能力拓展
1、观察下列图形的排列规律(其中▼□☆分别代表三角形,正方形,五角星)▼□☆▼▼□☆▼□☆▼▼□☆▼┅┅若第一个图形是三角形,则第2008个图形是___________.(填名称)
2.以给定的图形“ΟΟΔΔ═”(两个圆,两个三角形,两条平行线)为构件,构思独特且有意义的图形.并写出一两句贴切诙谐的解说词.
六、小结:同学们各抒己见,说出自己的收获或感受。
七、作业:完成配套练习册中1.1我们身边的图形世界。
1.2 几何图形(第一课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、认识点、线、面、体,感受它们之间的关系
2、以运动的观点看点、线、面、体。
二、知识回顾
1、 、 、 、 等都是几何体。
2、构成几何体的面有 、 。
三、预习新知:
1、几何图形是由 、 、 、 组成的。
2、点动成 ,线动成 ,面动成 。
3、几何图形可分为 图形和 图形。
四、导学探究
1、几何图形
(1)读课本7-8页完成观察与思考(1)、(2)、(3)、(4)提出的问题
(2)面面相交成 ,线线相交成
(3) 、 、 、 以及他们的组合都是几何图形。
2、运动的观点看点、线、面、体
(1)读课本观察与思考(5),我们用运动的观点看点、线、面、体
点动成 ,线动成 ,面动成 。
(2)开动你的大脑在举出几个实例来吧。
3、图形的分类
(1)读课本观察与思考(6)
(2)如果一个几何图形上的点 ,那么这样的几何图形叫做
。例如: , 等都是立体图形。
(3)如果一个几何图形上的点 ,那么这样的几何图形叫做
。例如: , 等都是平面图形。
4、练习:
(1)把铅笔尖看做一个点,让铅笔尖在白纸上移动,你有什么发现?
(2)钟表上的分针转动一周形成一个圆面,说明了什么道理?
(3)一枚硬币在光滑的桌面上旋转一周形成一个球,说明了什么道理?
五、当堂达标
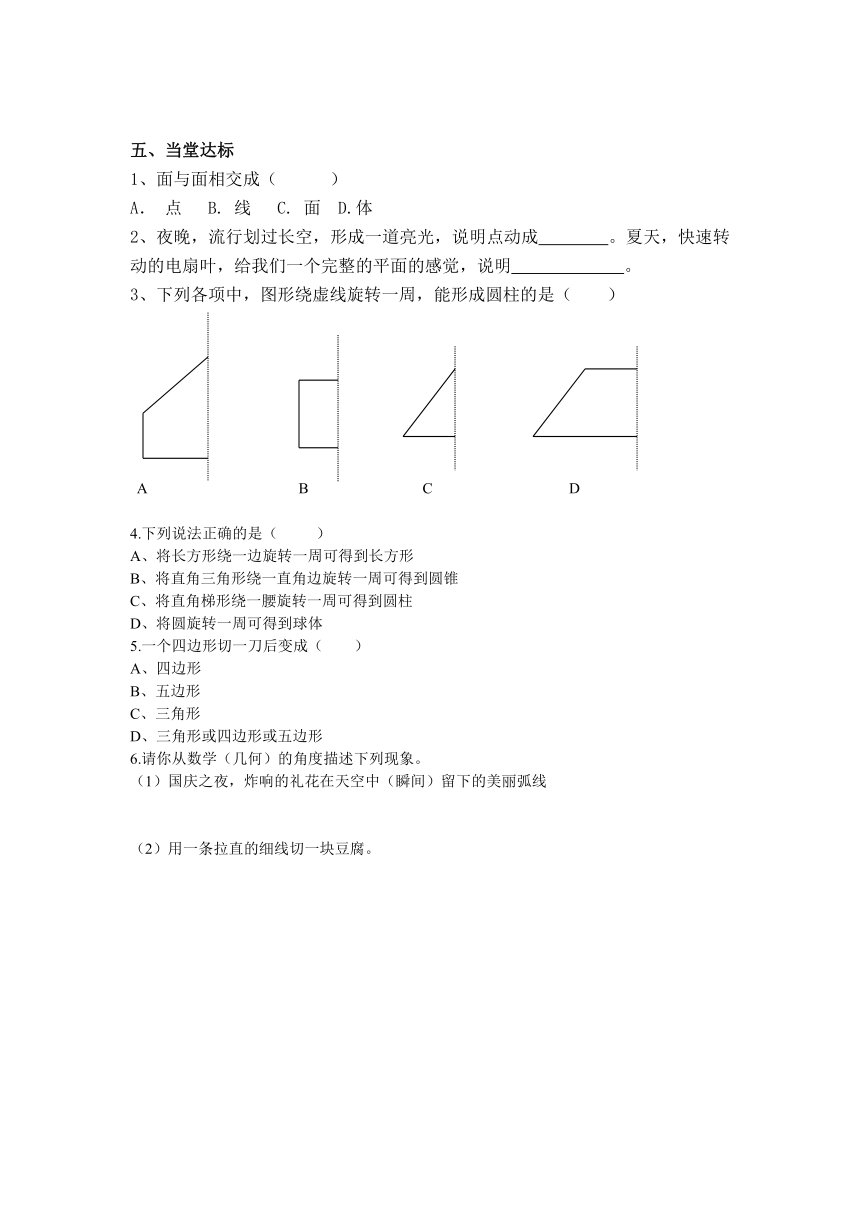
1、面与面相交成( )
A. 点 B. 线 C. 面 D.体
2、夜晚,流行划过长空,形成一道亮光,说明点动成 。夏天,快速转动的电扇叶,给我们一个完整的平面的感觉,说明 。
3、下列各项中,图形绕虚线旋转一周,能形成圆柱的是( )
A B C D
4.下列说法正确的是( )
A、将长方形绕一边旋转一周可得到长方形
B、将直角三角形绕一直角边旋转一周可得到圆锥
C、将直角梯形绕一腰旋转一周可得到圆柱
D、将圆旋转一周可得到球体
5.一个四边形切一刀后变成( )
A、四边形
B、五边形
C、三角形
D、三角形或四边形或五边形
6.请你从数学(几何)的角度描述下列现象。
(1)国庆之夜,炸响的礼花在天空中(瞬间)留下的美丽弧线
(2)用一条拉直的细线切一块豆腐。
1.2 几何图形 (第二课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、会判断一个图形是否是立方体的平面展开图
2、会利用展开图制作立方体模型
二、知识回顾:
1、几何图形是由 、 、 、
2、点动成 ,线动成 ,面动成 。
3、几何图形可分为 图形和 图形。
三、预习新知
1、立方体有 个面, 条棱, 个顶点。
四、导学探究
探究1、正方体
(1)、如图是一个正方体形状的包装盒,它是由几个面围成的?
各个面的形状是怎样的平面图形?
这些图形的大小 形状都相同吗?
(2)数一数,正方体有 个顶点。 条棱。这些棱的长短都一样吗?
(3)正方体的每个顶点处有 条棱,他们都在同一个平面上吗?
(4)从包装盒的一个顶点出发,沿它的一些棱剪开。想一想你至少要剪开 条棱就可以把包装盒的各个面铺在同一个平面上.
(5)将正方体包装盒的各个面按不同的方向分别标上汉子“上、下、前、后、左、右”。沿条数最少的棱剪开后,铺在桌面上。观察你得到的图形的形状,与周围同学得到的平面图形的形状一样吗? 。 它们有哪些相同和不同?与同学交流
探究2、正方体的平面展开图
例: 相同的立方体图形,按不同的方式展开得到的平面展开图有多种,正方体的平面展开图有很多种,正方体的平面展开图共有11种。
+
观察下列平面图,能否组成立方体:
观察图形,你一定会有新的发现,什么样的平面图形一定不能构成正方体。
探究三.正方体的相对的面
(1)、图.,是一个利用硬纸板制作正方体的折叠过程。你能说出在图中,与1号面,2号面,3号面向对的面各是几号面吗?与同学交流。
(2)、6个大小相同、连在一起的正方形,如果能折叠成正方体,你发现在这个正方形相对的面之间与原平面图形的各个正方形之间的位置排列存在什么规律?找找看,与同学交流。
4练一练:完成课本11页的练习。
五、小结:谈谈本节课的收获。
六、作业:完成课本12页,4、5、6.
1.3线段、射线、和直线 (第一课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、.加深和拓展一、二学段所学的线段、射线和直线的内容,能辨别线段、射线和直线,说明它们的区别和联系
2、能按要求画出直线、射线和线段,并能用字母正确的表示这些图形,感受符合在描述图形中的重要作用
二、预习新知:
1、线段有 个端点,线段有长度。
2、射线有 个端点,射线没有长度。
3、直线 端点,也没有长度。
三、导学探究
探究一 线段、射线、直线(课本13-14)
1线段:
如图:
线段有 个端点,有长度。
可表示为: 、 、 。
2射线:
如图:将线段向一个方向延伸就得到射线
射线有 个端点, 长度。
如图可表示为: 、
3直线:
如图:把线段向两个方向无限延伸,就得到直线。
。
直线 端点, 长度
如图可表示为: 、 、 。
4讨论:线段、射线、直线之间的相同点和不同点
探究二:例1
如图,A,B,C是直线l上的3个点
图中共有几条线段,这些线段应该怎样表示?
图中一点B为端点的射线有几条?怎样表示?
直线l还可以怎样表示?
练一练:完成课本15页的练习
小结:谈一谈本节课的收获
四 当堂达标
1、线段有 个端点,射线有 个端点,直线有 个端点。
2、判断正误:
(1)直线是射线长度的2倍 ( )
(2)射线AB和射线BA是同一条射线( 0
(3)直线AB与直线BA是同一条直线( )
(4)延长射线AB ( )
(5)经过三点可确定3条直线 (
3、下列说法正确的是( )
A画一条3cm长的直线
B画一条3cm长的射线
C画一条3cm长的线段
D在直线、射线、线段中只有射线有长度
4、图中的线段共有就( )
A、4条 B 5条 C 7条 D 8条
5、如图所示,下列说法不正确的是( )
A直线AB与直线BA是同一条直线
B射线OA与射线OB是同一条射线
C 射线OA与射线AB是同一条射线
D线段AB与线段BA是同一条线段
五、能力提升
1、(1)、一条线段AB上有1个点P1,共有 条线段。
(2)、一条线段AB上有2个点P1、P2,共有 条线段。
(3)、 一条线段AB上有3个点P1、P2、P3,共有 条线段。
(4)、一条线段上有n个点,共有 条线段。(包括线段的两个端点)
2、4支球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),则总的比赛场数为 场。
六、作业:习题1.3的1、2题
1.3线段、射线和直线(第二课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、了解两点确定一条直线的事实,认识两条直线相交位置关系
2、能用实例和操作,验证两条直线相交,只能有一个交点。
二、知识回顾:
1、线段有 个端点,线段有长度。可以用表示端点的 个大写字母表示 。
2、射线有 个端点,射线没有长度。可以用两个大写字母表示,表示端点的字母必须在 。
3、直线 端点,也没有长度。可以用直线上的表示任意两个点的大写字母表示。
三、预习新知
1、经过一点可以画 条直线,经过两点 画一条直线,也就是说
四、导学探究
探究一:点和直线的位置关系
1、自读课本(15-16)观察与思考,一个点与一条直线有 种位置关系。
2、如图所示,一个点P与直线l有位置关系有两种:
(1)
如图, ,或者说
(2)
如图, ,或者说
探究二:直线和直线的位置关系
用直尺过点作直线:
过一点A能作 条直线。
过两点A、B能作 条直线。
经过一点可以作无数条直线,经过两点 作一条直线,
也就是说
2、两条直线相交
如果两条直线经过同一点,就称这两条直线 ;这时两条直线有唯一的公共点,这个公共点叫做它们的 。
如图: ,
。
想一想,平面上的两条直线,除相交之外,还有其它的位置关系吗?
平面上的两条直线有两种位置关系: 、 。
练一练:完成课本17页的练习
五、当堂达标
1、如图所示,点A在直线 上,在直线 外;
直线a经过点 和点 ,
直线b不经过点 ,直线a,b相交于点
我们在用玩具枪瞄准时,总是用一只眼对准准星
和目标,用数学知识解释这是因为
3、在一面墙上钉一根木条,若木条能随意转动,需要钉上 个钉子,
若 木条不能转动,至少需要订上 个钉子,依据是
4、过平面上的四点最多可以作 条直线,最少可以作 。
六、挑战自我:
1、两条直线相交,能不能有两个交点?为什么?
2、平面上的2条直线,最多有 个交点。
3、平面上的3条直线,最多有 个交点。
4、平面上的4条直线,最多有 个交点。
5、平面上的5条直线,最多有 个交点。
你发现了什么规律?与同学交流。
七、小结:本节课有什么新的收获?
八、作业:习题1.3 3、4、5题
1、4线段的比较与作法(第一课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
学习目标:
能用直尺、圆规比较两条线段的长短,并会用符号“>”“<”、“=”表示出来。
了解“两点间所有连线段最短”的性质
理解两点间的距离
知识回顾
1、线段有 个端点,线段有长度。射线有 个端点,射线没有长度。直线 端点,也没有长度。
三、预习新知:
1、两点间所有连线中, 最短。简称
2、两点之间 的 ,叫做这两点间的距离 。
四、导学探究:
探究一:线段的比较
1、阅读课本18页 实验与探究
要比较两条线段AB 与CD的长短, 可以把其中的一条线段AB移到另一条线段CD上,使点A和点C重合。
如图,
如果点B落在C,D之间,那么就说 记作:
(2)如图,
如果点B和点C重合, 那么就说 记作:
(3)如图,
如果点B落在线段CD的延长线上,那么就说 记作:
实际比较两条线段AB与CD的长短,还可以借助圆规来进行,如课本图1-26,1-27所示,你能说明这种方法和它的道理吗?
探究二:线段的性质
阅读课本19页交流与发现
2、如果把图中的三条线拉直,并把它们都看成是线段,然后比较这些线段的大小,可以知道 最短。
3、这就是说,两点间的所有连线中 ,可以简单说成
探究三:两点间的距离
1、两点之间线段的 ,叫做这两点间的距离。
如:A、B两点间的距离是( )厘米
探究四:例题
例:如图,比较点A、B和C两两之间距离的大小。
练一练:完成课本20页的练习。
五、当堂达标:
1、从 A地到B地架设电线,总是尽可能沿着线段AB架设,这是因为:
。
2、某工程队在修建高速公路时,有时需将弯曲的道路改直,根据什么可以说明这样作能缩短路程( )
A两点之间所有连线中,线段最短。
B两点确定一条直线。
C过一点有无数条直线
D以上都不对
3、下列说法正确的是( )
A、两条射线 B、两条直线
C、直线与射线 D、两条线段
4、如图,下列各式中错误的是( )
A、AB=AD+DB B、CB=AB-AC
C、CB-DB=CD D、CB-DB=AC
5、如图,AB=CD,则AC与BD之间的大小关系( )
A、AC>BD B 、ACC、AC=BD D、不能确定
六、课堂小结:
同学互相交流今天的收获。
1、4线段的比较与作法(第二课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、会进行简单的尺规作图
2、了解线段中点的概念
二、知识回顾:
两点之间 。
两点之间线段的 ,叫做这两点之间的距离。
预习新知:
点M把线段AB分成相等的两条线段AM与BM,那么点M叫做线段 。
导学探究:
探究一:简单的尺规作图
例2:用直尺和圆规作一条线段,使它等于已知线段。
已知:线段a
求作:线段AB,使AB=a.
作法:(1)用直尺作 。
(2)用圆规在射线AC上 。
就是与线段a线段的 。
拓展:如图,已知线段a,线段b
探究二:线段的中点
1、如何把线段AB分成相等的两部分。
如果 把线段AB分成相等的两条线段 ,
那么点 叫做线段AB的 。
这时AM=BM= 。或AB= 。
2、类似的,还可将线段AB分成三等分,四等分。
点 、点 叫线段AB的三等分点。
点 、点 点 叫线段AB的四等分点。
练一练:
(1)已知线段a用直尺和圆规作一条线段AB,使它的长度等于2a.
(2)如图,D为线段CB的中点,AD=8厘米,AB=10厘米,求CB的长度
四、当堂达标
1、 如图所示,C为AB的中点,AC=3cm,则AB= cm.
2、 在直线上截取线段AB,使AB=8cm,BC=3cm,则线段AC的长为( )
A、11cm B、 5cm C 、11cm或5cm D、 7cm
3、如图,延长线段AB到C,使BC=4,若AB=8,则线段AC的长是BC的 倍。
4、已知线段AB=7cm,在直线AB上画线段BC,使BC=3cm,则线段AC的长为 cm.
5、如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10,AC=6,则CD= 。
6、如图所示,线段AB=8cm,C是线段AB上一点,且AC=3.2cm,M是线段AB的中点,N是线段AC的中点,则MN= cm
.
.
A
B
a
.
.
A
B
l
.
.
A
B
l
.
.
A
B
C
.
A
B
C
D
E
.
.
O
A
B
.
.
P
l
.
P
l
.
A
.
A
.
B
A
B
C
D
.
O
A
b
a
.
O
.
.
A
B
C
D
.
D
C
.
.
A
B
.
.
A
B
C
D
.
A
B
.
.
A
B
.
.
A
B
C
.
D
C
.
.
A
B
D
.
.
C
.
.
A
B
D
.
.
a
(1)已知线段a与b,作一条线段AC=a+b
已知:
求作:
做法:
(2)已知线段a与b,作一条线段AC=a-b
已知:
求作
做法:
a
b
A
B
A
B
A
B
a
C
.
.
A
B
D
.
.
C
.
.
A
B
.
C
.
.
A
B
.
C
.
.
A
B
D
.
.
C
.
.
A
B
M
.
.
.
N
1.1我们身边的图形世界学案
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1.能说出一些常见的几何体、平面图形。
2.能识别生活中的几何体
3.能识别优美图案中的平面图形。
二、自主预习
1.如果对于我们看到的物体,只研究它们的 、 、 ,
而不考虑 、 、 等其他性质时,就得到各种几何体,几何体简称 。
2.镜面、黑板面、操场、平静的水面等都给我们以 的形象。数学上所说的平面是从所有具备这种形象的事物中抽象出来的,平面没有厚薄,没有边界,是向四面八方 。
3.生活中,除了平面的形象外,还有 的形象。
4.体是由 围成的。
三、导学探究
1.几何体
(1).独立看书第4页-第5页,观察与思考,尽可能的完成书上提出的有关问题和练习。(对于出现的疑难问题,可采用学生交流讨论)
(2)几何体简称 ,我们只研究他们的 、 、 。
(3)举出一些你熟悉的几何体,至少5个。
。
2.面
(1)生活中,我们见到很多平面的例子,请举出一些。
(2)生活中,除了平面的形象外,你还会经常见到曲的面的形象。请举出一些。
3.体和面的关系
是由 围成的。请举出一些例子。(小组之间可以交流)
4.练习
(1)、独立完成课本上的练习1-2
(2)、完成习题1.1,并与同学交流。
四、当堂达标
1.找出生活中与下列几何体形状类似的物体各一个.
(1)正方体:_______ (2)圆柱 :_______
(4)长方体 :_______ (5) 圆锥:_______ (6)球 :_______
2.由生活中的物体抽象出几何图形,在后面的横线上填出对应的几何体.
收音机_______ 杯子_______ 砖块_______
纸箱_______ 足球_______ 易拉罐_______ 粉笔盒_______
堆沙子_______ 魔方_______
3.判断下列的陈述是否正确:
(1)圆柱、圆锥的底面都是圆( )
(2)圆柱的侧面是平面( )
4.如图,
足球呈现的形状是_______,
它由一个_______面组成,
球面上的多边形是_______.
2.下列图形中包含哪些简单的平面图形?
(3)下列标注的图形名称与图形不相符的是:( )
A 球 B 长方体 C 圆柱 D 圆锥
五、能力拓展
1、观察下列图形的排列规律(其中▼□☆分别代表三角形,正方形,五角星)▼□☆▼▼□☆▼□☆▼▼□☆▼┅┅若第一个图形是三角形,则第2008个图形是___________.(填名称)
2.以给定的图形“ΟΟΔΔ═”(两个圆,两个三角形,两条平行线)为构件,构思独特且有意义的图形.并写出一两句贴切诙谐的解说词.
六、小结:同学们各抒己见,说出自己的收获或感受。
七、作业:完成配套练习册中1.1我们身边的图形世界。
1.2 几何图形(第一课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、认识点、线、面、体,感受它们之间的关系
2、以运动的观点看点、线、面、体。
二、知识回顾
1、 、 、 、 等都是几何体。
2、构成几何体的面有 、 。
三、预习新知:
1、几何图形是由 、 、 、 组成的。
2、点动成 ,线动成 ,面动成 。
3、几何图形可分为 图形和 图形。
四、导学探究
1、几何图形
(1)读课本7-8页完成观察与思考(1)、(2)、(3)、(4)提出的问题
(2)面面相交成 ,线线相交成
(3) 、 、 、 以及他们的组合都是几何图形。
2、运动的观点看点、线、面、体
(1)读课本观察与思考(5),我们用运动的观点看点、线、面、体
点动成 ,线动成 ,面动成 。
(2)开动你的大脑在举出几个实例来吧。
3、图形的分类
(1)读课本观察与思考(6)
(2)如果一个几何图形上的点 ,那么这样的几何图形叫做
。例如: , 等都是立体图形。
(3)如果一个几何图形上的点 ,那么这样的几何图形叫做
。例如: , 等都是平面图形。
4、练习:
(1)把铅笔尖看做一个点,让铅笔尖在白纸上移动,你有什么发现?
(2)钟表上的分针转动一周形成一个圆面,说明了什么道理?
(3)一枚硬币在光滑的桌面上旋转一周形成一个球,说明了什么道理?
五、当堂达标
1、面与面相交成( )
A. 点 B. 线 C. 面 D.体
2、夜晚,流行划过长空,形成一道亮光,说明点动成 。夏天,快速转动的电扇叶,给我们一个完整的平面的感觉,说明 。
3、下列各项中,图形绕虚线旋转一周,能形成圆柱的是( )
A B C D
4.下列说法正确的是( )
A、将长方形绕一边旋转一周可得到长方形
B、将直角三角形绕一直角边旋转一周可得到圆锥
C、将直角梯形绕一腰旋转一周可得到圆柱
D、将圆旋转一周可得到球体
5.一个四边形切一刀后变成( )
A、四边形
B、五边形
C、三角形
D、三角形或四边形或五边形
6.请你从数学(几何)的角度描述下列现象。
(1)国庆之夜,炸响的礼花在天空中(瞬间)留下的美丽弧线
(2)用一条拉直的细线切一块豆腐。
1.2 几何图形 (第二课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、会判断一个图形是否是立方体的平面展开图
2、会利用展开图制作立方体模型
二、知识回顾:
1、几何图形是由 、 、 、
2、点动成 ,线动成 ,面动成 。
3、几何图形可分为 图形和 图形。
三、预习新知
1、立方体有 个面, 条棱, 个顶点。
四、导学探究
探究1、正方体
(1)、如图是一个正方体形状的包装盒,它是由几个面围成的?
各个面的形状是怎样的平面图形?
这些图形的大小 形状都相同吗?
(2)数一数,正方体有 个顶点。 条棱。这些棱的长短都一样吗?
(3)正方体的每个顶点处有 条棱,他们都在同一个平面上吗?
(4)从包装盒的一个顶点出发,沿它的一些棱剪开。想一想你至少要剪开 条棱就可以把包装盒的各个面铺在同一个平面上.
(5)将正方体包装盒的各个面按不同的方向分别标上汉子“上、下、前、后、左、右”。沿条数最少的棱剪开后,铺在桌面上。观察你得到的图形的形状,与周围同学得到的平面图形的形状一样吗? 。 它们有哪些相同和不同?与同学交流
探究2、正方体的平面展开图
例: 相同的立方体图形,按不同的方式展开得到的平面展开图有多种,正方体的平面展开图有很多种,正方体的平面展开图共有11种。
+
观察下列平面图,能否组成立方体:
观察图形,你一定会有新的发现,什么样的平面图形一定不能构成正方体。
探究三.正方体的相对的面
(1)、图.,是一个利用硬纸板制作正方体的折叠过程。你能说出在图中,与1号面,2号面,3号面向对的面各是几号面吗?与同学交流。
(2)、6个大小相同、连在一起的正方形,如果能折叠成正方体,你发现在这个正方形相对的面之间与原平面图形的各个正方形之间的位置排列存在什么规律?找找看,与同学交流。
4练一练:完成课本11页的练习。
五、小结:谈谈本节课的收获。
六、作业:完成课本12页,4、5、6.
1.3线段、射线、和直线 (第一课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、.加深和拓展一、二学段所学的线段、射线和直线的内容,能辨别线段、射线和直线,说明它们的区别和联系
2、能按要求画出直线、射线和线段,并能用字母正确的表示这些图形,感受符合在描述图形中的重要作用
二、预习新知:
1、线段有 个端点,线段有长度。
2、射线有 个端点,射线没有长度。
3、直线 端点,也没有长度。
三、导学探究
探究一 线段、射线、直线(课本13-14)
1线段:
如图:
线段有 个端点,有长度。
可表示为: 、 、 。
2射线:
如图:将线段向一个方向延伸就得到射线
射线有 个端点, 长度。
如图可表示为: 、
3直线:
如图:把线段向两个方向无限延伸,就得到直线。
。
直线 端点, 长度
如图可表示为: 、 、 。
4讨论:线段、射线、直线之间的相同点和不同点
探究二:例1
如图,A,B,C是直线l上的3个点
图中共有几条线段,这些线段应该怎样表示?
图中一点B为端点的射线有几条?怎样表示?
直线l还可以怎样表示?
练一练:完成课本15页的练习
小结:谈一谈本节课的收获
四 当堂达标
1、线段有 个端点,射线有 个端点,直线有 个端点。
2、判断正误:
(1)直线是射线长度的2倍 ( )
(2)射线AB和射线BA是同一条射线( 0
(3)直线AB与直线BA是同一条直线( )
(4)延长射线AB ( )
(5)经过三点可确定3条直线 (
3、下列说法正确的是( )
A画一条3cm长的直线
B画一条3cm长的射线
C画一条3cm长的线段
D在直线、射线、线段中只有射线有长度
4、图中的线段共有就( )
A、4条 B 5条 C 7条 D 8条
5、如图所示,下列说法不正确的是( )
A直线AB与直线BA是同一条直线
B射线OA与射线OB是同一条射线
C 射线OA与射线AB是同一条射线
D线段AB与线段BA是同一条线段
五、能力提升
1、(1)、一条线段AB上有1个点P1,共有 条线段。
(2)、一条线段AB上有2个点P1、P2,共有 条线段。
(3)、 一条线段AB上有3个点P1、P2、P3,共有 条线段。
(4)、一条线段上有n个点,共有 条线段。(包括线段的两个端点)
2、4支球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),则总的比赛场数为 场。
六、作业:习题1.3的1、2题
1.3线段、射线和直线(第二课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、了解两点确定一条直线的事实,认识两条直线相交位置关系
2、能用实例和操作,验证两条直线相交,只能有一个交点。
二、知识回顾:
1、线段有 个端点,线段有长度。可以用表示端点的 个大写字母表示 。
2、射线有 个端点,射线没有长度。可以用两个大写字母表示,表示端点的字母必须在 。
3、直线 端点,也没有长度。可以用直线上的表示任意两个点的大写字母表示。
三、预习新知
1、经过一点可以画 条直线,经过两点 画一条直线,也就是说
四、导学探究
探究一:点和直线的位置关系
1、自读课本(15-16)观察与思考,一个点与一条直线有 种位置关系。
2、如图所示,一个点P与直线l有位置关系有两种:
(1)
如图, ,或者说
(2)
如图, ,或者说
探究二:直线和直线的位置关系
用直尺过点作直线:
过一点A能作 条直线。
过两点A、B能作 条直线。
经过一点可以作无数条直线,经过两点 作一条直线,
也就是说
2、两条直线相交
如果两条直线经过同一点,就称这两条直线 ;这时两条直线有唯一的公共点,这个公共点叫做它们的 。
如图: ,
。
想一想,平面上的两条直线,除相交之外,还有其它的位置关系吗?
平面上的两条直线有两种位置关系: 、 。
练一练:完成课本17页的练习
五、当堂达标
1、如图所示,点A在直线 上,在直线 外;
直线a经过点 和点 ,
直线b不经过点 ,直线a,b相交于点
我们在用玩具枪瞄准时,总是用一只眼对准准星
和目标,用数学知识解释这是因为
3、在一面墙上钉一根木条,若木条能随意转动,需要钉上 个钉子,
若 木条不能转动,至少需要订上 个钉子,依据是
4、过平面上的四点最多可以作 条直线,最少可以作 。
六、挑战自我:
1、两条直线相交,能不能有两个交点?为什么?
2、平面上的2条直线,最多有 个交点。
3、平面上的3条直线,最多有 个交点。
4、平面上的4条直线,最多有 个交点。
5、平面上的5条直线,最多有 个交点。
你发现了什么规律?与同学交流。
七、小结:本节课有什么新的收获?
八、作业:习题1.3 3、4、5题
1、4线段的比较与作法(第一课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
学习目标:
能用直尺、圆规比较两条线段的长短,并会用符号“>”“<”、“=”表示出来。
了解“两点间所有连线段最短”的性质
理解两点间的距离
知识回顾
1、线段有 个端点,线段有长度。射线有 个端点,射线没有长度。直线 端点,也没有长度。
三、预习新知:
1、两点间所有连线中, 最短。简称
2、两点之间 的 ,叫做这两点间的距离 。
四、导学探究:
探究一:线段的比较
1、阅读课本18页 实验与探究
要比较两条线段AB 与CD的长短, 可以把其中的一条线段AB移到另一条线段CD上,使点A和点C重合。
如图,
如果点B落在C,D之间,那么就说 记作:
(2)如图,
如果点B和点C重合, 那么就说 记作:
(3)如图,
如果点B落在线段CD的延长线上,那么就说 记作:
实际比较两条线段AB与CD的长短,还可以借助圆规来进行,如课本图1-26,1-27所示,你能说明这种方法和它的道理吗?
探究二:线段的性质
阅读课本19页交流与发现
2、如果把图中的三条线拉直,并把它们都看成是线段,然后比较这些线段的大小,可以知道 最短。
3、这就是说,两点间的所有连线中 ,可以简单说成
探究三:两点间的距离
1、两点之间线段的 ,叫做这两点间的距离。
如:A、B两点间的距离是( )厘米
探究四:例题
例:如图,比较点A、B和C两两之间距离的大小。
练一练:完成课本20页的练习。
五、当堂达标:
1、从 A地到B地架设电线,总是尽可能沿着线段AB架设,这是因为:
。
2、某工程队在修建高速公路时,有时需将弯曲的道路改直,根据什么可以说明这样作能缩短路程( )
A两点之间所有连线中,线段最短。
B两点确定一条直线。
C过一点有无数条直线
D以上都不对
3、下列说法正确的是( )
A、两条射线 B、两条直线
C、直线与射线 D、两条线段
4、如图,下列各式中错误的是( )
A、AB=AD+DB B、CB=AB-AC
C、CB-DB=CD D、CB-DB=AC
5、如图,AB=CD,则AC与BD之间的大小关系( )
A、AC>BD B 、AC
六、课堂小结:
同学互相交流今天的收获。
1、4线段的比较与作法(第二课时)
终兴中学 编写人 王敏 王中华 郑莉 审阅人 吴吉杰
一、学习目标:
1、会进行简单的尺规作图
2、了解线段中点的概念
二、知识回顾:
两点之间 。
两点之间线段的 ,叫做这两点之间的距离。
预习新知:
点M把线段AB分成相等的两条线段AM与BM,那么点M叫做线段 。
导学探究:
探究一:简单的尺规作图
例2:用直尺和圆规作一条线段,使它等于已知线段。
已知:线段a
求作:线段AB,使AB=a.
作法:(1)用直尺作 。
(2)用圆规在射线AC上 。
就是与线段a线段的 。
拓展:如图,已知线段a,线段b
探究二:线段的中点
1、如何把线段AB分成相等的两部分。
如果 把线段AB分成相等的两条线段 ,
那么点 叫做线段AB的 。
这时AM=BM= 。或AB= 。
2、类似的,还可将线段AB分成三等分,四等分。
点 、点 叫线段AB的三等分点。
点 、点 点 叫线段AB的四等分点。
练一练:
(1)已知线段a用直尺和圆规作一条线段AB,使它的长度等于2a.
(2)如图,D为线段CB的中点,AD=8厘米,AB=10厘米,求CB的长度
四、当堂达标
1、 如图所示,C为AB的中点,AC=3cm,则AB= cm.
2、 在直线上截取线段AB,使AB=8cm,BC=3cm,则线段AC的长为( )
A、11cm B、 5cm C 、11cm或5cm D、 7cm
3、如图,延长线段AB到C,使BC=4,若AB=8,则线段AC的长是BC的 倍。
4、已知线段AB=7cm,在直线AB上画线段BC,使BC=3cm,则线段AC的长为 cm.
5、如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10,AC=6,则CD= 。
6、如图所示,线段AB=8cm,C是线段AB上一点,且AC=3.2cm,M是线段AB的中点,N是线段AC的中点,则MN= cm
.
.
A
B
a
.
.
A
B
l
.
.
A
B
l
.
.
A
B
C
.
A
B
C
D
E
.
.
O
A
B
.
.
P
l
.
P
l
.
A
.
A
.
B
A
B
C
D
.
O
A
b
a
.
O
.
.
A
B
C
D
.
D
C
.
.
A
B
.
.
A
B
C
D
.
A
B
.
.
A
B
.
.
A
B
C
.
D
C
.
.
A
B
D
.
.
C
.
.
A
B
D
.
.
a
(1)已知线段a与b,作一条线段AC=a+b
已知:
求作:
做法:
(2)已知线段a与b,作一条线段AC=a-b
已知:
求作
做法:
a
b
A
B
A
B
A
B
a
C
.
.
A
B
D
.
.
C
.
.
A
B
.
C
.
.
A
B
.
C
.
.
A
B
D
.
.
C
.
.
A
B
M
.
.
.
N
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
