14.2.1平方差公式 同步练习 2021-2022学年人教版八年级数学上册(word版含答案)
文档属性
| 名称 | 14.2.1平方差公式 同步练习 2021-2022学年人教版八年级数学上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 229.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 10:48:49 | ||
图片预览




文档简介
平方差公式
一、单选题
1.运用乘法公式计算(4+x)(x﹣4)的结果是( )
A.x2﹣16 B.x2+16 C.16﹣x2 D.﹣x2﹣16
2.已知,则的值为( )
A.5 B.10 C.15 D.25
3.下列各式不能用平方差公式计算的是( )
A. B.
C. D.
4.如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”(如8,,则8,16均为“和谐数”),在不超过80的正整数中,所有的“和谐数”之和为( )
A.430 B.440 C.450 D.460
5.下列各式中,不能用平方差公式计算的是( )
A. B.
C. D.
6.若,则的值为( )
A.4 B.2 C.0 D.
7.计算结果等于( )
A.1 B.316-216 C.332+232 D.332-232
8.若规定m n=mn(m﹣n),则(a+b) (a﹣b)的值( )
A.2ab2﹣2b2 B.2a2b﹣2b3 C.2a2b+2b2 D.2ab﹣2ab2
9.计算:的结果,正确的是( )
A. B. C. D.
10.下列算式能用平方差公式计算的是( )
A. B. C. D.
11.将图甲中明影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于、的恒等式为( )
A. B.
C. D.
12.如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中大正方形的面积为64,小正方形的面积为9.若用x,y分别表示小长方形的长与宽(其中x>y),则下列关系式中错误的是( )
A. B.
C. D.
13.计算(1)(1)……(1)(1)的值是( )
A. B. C. D.
二、填空题
14.填空:(2a+b)(______)=b2﹣4a2
15.已知|x﹣1|+|y+2|=0,则(2x+y)(2x﹣y)=___.
16.一个长方体文具盒,长、宽、高如图所示(单位:cm),该文具盒的体积是________.
17.已知是二元一次方程组的解,则________.
18.如图是一个数值转换器,若输入的数是2021,则输出的数是______.
三、解答题
19.用乘法公式简算
(1)199×201 (2)20132﹣2014×2012
20.先化简,再求值.6x2﹣(2x+1)(3x﹣2)+(x+3)(x﹣3),其中x=﹣2.
21.若(x﹣2)(x2+ax﹣8b)的展开式中不含x的二次项和一次项.
(1)求b的值;
(2)求(a+1)(a2+1)(a4+1)…(a32+1)+1的值.
22.探究下面的问题:
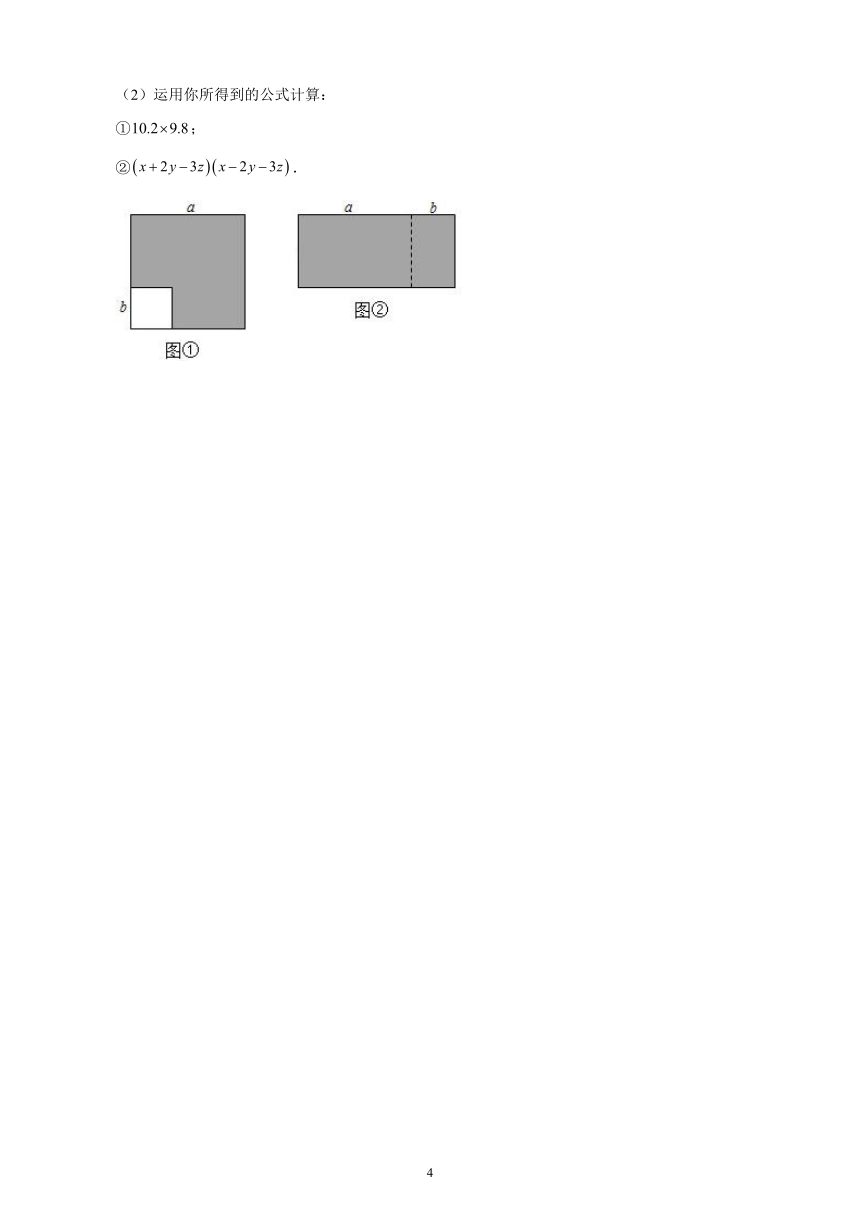
(1)如图①,在边长为的正方形中去掉一个边长为的小正方形(),把余下的部分剪拼成如图②的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是______(用式子表示);
(2)运用你所得到的公式计算:
①;
②.
参考答案
1.A
解:(4+x)(x 4)
=(x+4)(x 4)
=x2 42
=x2 16,
故选:A.
2.D
解:∵ a b=5 ,
∴原式
.
故选:D.
3.B
解:符合平方差公式的结构, 能用平方差公式计算;
不符合平方差公式的结构, 不能用平方差公式计算;
符合平方差公式的结构, 能用平方差公式计算;
符合平方差公式的结构, 能用平方差公式计算.
故选B.
4.B
解:∵212 192=(21+19)(21 19)=80,
∴在不超过80的正整数中,所有的“和谐数”之和为:
( 12+32)+( 32+52)+( 52+72)+……+( 192+212)
=212 12
=(21+1)(21 1)
=22×20
=440,
故选:B.
5.B
解:A.(-a-b)(a-b)=(-b)2-a2,此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;
B.(-x-2y)(x+2y),不符合平方差公式的特征,不能用平方差公式计算,故此选项符合题意;
C.(2x2-y2)(2x2+y2)=(2x2)2-(y2)2,此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;
D.(2a+b-c)(2a-b-c)=(2a-c)2-b2,此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意,
故选:B.
6.D
解:原式,
,
,
,
故选:D.
7.B
解:
故选B.
8.B
解:根据题中的新定义得:
(a+b) (a﹣b)
=(a+b)(a﹣b)(a+b﹣a+b)
=2b(a2﹣b2)
=2a2b﹣2b3.
故选B.
9.A
解:
=
故选:A.
10.D
解:.该式子中两项均为相反项,不能用平方差公式计算,故本选项不符合题意.
.该式子中只有一个相同项,没有相反项,不能用平方差公式计算,故本选项不符合题意.
.该式子中既没有相同项,也没有相反项,不能用平方差公式计算,故本选项不符合题意.
.,既有相同项,也有相反项,能用平方差公式计算,故本选项符合题意.
故选:D.
11.C
解:图甲中图形的面积为:,
图乙中图形的面积为:,
∴,
故选:C.
12.D
解:A、因为正方形图案面积从整体看是64,从组合来看,可以是(x+y)2,还可以是(4xy+9),即4xy+9=64,故此选项正确;
B、因为正方形图案的边长8,同时还可用(x+y)来表示,故此选项正确;
C、中间小正方形的边长为3,同时根据长方形长宽也可表示为x-y,故此选项正确;
D、根据A、B可知x+y=8,x-y=3,则x2-y2=(x+y)(x-y)=24,故此选项错误;
故选:D.
13.D
解:
故答案为D
14.b-2a
解:因为(b+2a)(b-2a)=b2-4a2.
故答案为:b-2a.
15.0
解:根据题意得,x﹣1=0,y+2=0,
解答:x=1,y=﹣2,
∴(2x+y)(2x﹣y)=4x2﹣y2=4﹣4=0,
故答案为:0.
16.(a2-16)
解:根据题意得:文具盒的体积=(a+4)(a-4)×1=(a2-16)(),
故答案是:(a2-16)
17.-8
解:将代入方程组,可得,
①+②,得:3a+3b=12,
∴a+b=4,
①-②,得:a-b=-2,
∴a2-b2=(a+b)(a-b)=4×(-2)=-8,
故答案为:-8.
18.2023
解:由题意知,
当时,,
故答案为:2023.
19.(1)39999;(2)1
解:(1)原式=(200-1)×(200+1)
=2002-12
=40000-1
=39999;
(2)20132﹣(2013+1)×(2013-1)
=20132-20132+1
=1.
20.x2+x-7;-5
解:原式=6x2-6x2+4x-3x+2+x2-9
=x2+x-7,
当x=﹣2时,原式= ,
21.(1);(2)
解:(1)
展开式中不含x的二次项和一次项,
,
解得:,
;
(2)当时,
.
22.(1)a2 b2=(a+b)(a b);(2)①99.96;②x2 6xz+9z2 4y2
解:(1)图甲阴影面积=a2 b2,图乙阴影面积=(a+b)(a b),
∴得到的等式为:a2 b2=(a+b)(a b),
故答案为:a2 b2=(a+b)(a b);
(2)①10.2×9.8
=(10+0.2)×(10 0.2)
=102 0.22
=100 0.04
=99.96;
②
=(x 3z+2y)(x 3z 2y)
=(x 3z)2 (2y)2
=x2 6xz+9z2 4y2.
一、单选题
1.运用乘法公式计算(4+x)(x﹣4)的结果是( )
A.x2﹣16 B.x2+16 C.16﹣x2 D.﹣x2﹣16
2.已知,则的值为( )
A.5 B.10 C.15 D.25
3.下列各式不能用平方差公式计算的是( )
A. B.
C. D.
4.如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”(如8,,则8,16均为“和谐数”),在不超过80的正整数中,所有的“和谐数”之和为( )
A.430 B.440 C.450 D.460
5.下列各式中,不能用平方差公式计算的是( )
A. B.
C. D.
6.若,则的值为( )
A.4 B.2 C.0 D.
7.计算结果等于( )
A.1 B.316-216 C.332+232 D.332-232
8.若规定m n=mn(m﹣n),则(a+b) (a﹣b)的值( )
A.2ab2﹣2b2 B.2a2b﹣2b3 C.2a2b+2b2 D.2ab﹣2ab2
9.计算:的结果,正确的是( )
A. B. C. D.
10.下列算式能用平方差公式计算的是( )
A. B. C. D.
11.将图甲中明影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于、的恒等式为( )
A. B.
C. D.
12.如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中大正方形的面积为64,小正方形的面积为9.若用x,y分别表示小长方形的长与宽(其中x>y),则下列关系式中错误的是( )
A. B.
C. D.
13.计算(1)(1)……(1)(1)的值是( )
A. B. C. D.
二、填空题
14.填空:(2a+b)(______)=b2﹣4a2
15.已知|x﹣1|+|y+2|=0,则(2x+y)(2x﹣y)=___.
16.一个长方体文具盒,长、宽、高如图所示(单位:cm),该文具盒的体积是________.
17.已知是二元一次方程组的解,则________.
18.如图是一个数值转换器,若输入的数是2021,则输出的数是______.
三、解答题
19.用乘法公式简算
(1)199×201 (2)20132﹣2014×2012
20.先化简,再求值.6x2﹣(2x+1)(3x﹣2)+(x+3)(x﹣3),其中x=﹣2.
21.若(x﹣2)(x2+ax﹣8b)的展开式中不含x的二次项和一次项.
(1)求b的值;
(2)求(a+1)(a2+1)(a4+1)…(a32+1)+1的值.
22.探究下面的问题:
(1)如图①,在边长为的正方形中去掉一个边长为的小正方形(),把余下的部分剪拼成如图②的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是______(用式子表示);
(2)运用你所得到的公式计算:
①;
②.
参考答案
1.A
解:(4+x)(x 4)
=(x+4)(x 4)
=x2 42
=x2 16,
故选:A.
2.D
解:∵ a b=5 ,
∴原式
.
故选:D.
3.B
解:符合平方差公式的结构, 能用平方差公式计算;
不符合平方差公式的结构, 不能用平方差公式计算;
符合平方差公式的结构, 能用平方差公式计算;
符合平方差公式的结构, 能用平方差公式计算.
故选B.
4.B
解:∵212 192=(21+19)(21 19)=80,
∴在不超过80的正整数中,所有的“和谐数”之和为:
( 12+32)+( 32+52)+( 52+72)+……+( 192+212)
=212 12
=(21+1)(21 1)
=22×20
=440,
故选:B.
5.B
解:A.(-a-b)(a-b)=(-b)2-a2,此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;
B.(-x-2y)(x+2y),不符合平方差公式的特征,不能用平方差公式计算,故此选项符合题意;
C.(2x2-y2)(2x2+y2)=(2x2)2-(y2)2,此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意;
D.(2a+b-c)(2a-b-c)=(2a-c)2-b2,此题符合平方差公式的特征,能用平方差公式计算,故此选项不符合题意,
故选:B.
6.D
解:原式,
,
,
,
故选:D.
7.B
解:
故选B.
8.B
解:根据题中的新定义得:
(a+b) (a﹣b)
=(a+b)(a﹣b)(a+b﹣a+b)
=2b(a2﹣b2)
=2a2b﹣2b3.
故选B.
9.A
解:
=
故选:A.
10.D
解:.该式子中两项均为相反项,不能用平方差公式计算,故本选项不符合题意.
.该式子中只有一个相同项,没有相反项,不能用平方差公式计算,故本选项不符合题意.
.该式子中既没有相同项,也没有相反项,不能用平方差公式计算,故本选项不符合题意.
.,既有相同项,也有相反项,能用平方差公式计算,故本选项符合题意.
故选:D.
11.C
解:图甲中图形的面积为:,
图乙中图形的面积为:,
∴,
故选:C.
12.D
解:A、因为正方形图案面积从整体看是64,从组合来看,可以是(x+y)2,还可以是(4xy+9),即4xy+9=64,故此选项正确;
B、因为正方形图案的边长8,同时还可用(x+y)来表示,故此选项正确;
C、中间小正方形的边长为3,同时根据长方形长宽也可表示为x-y,故此选项正确;
D、根据A、B可知x+y=8,x-y=3,则x2-y2=(x+y)(x-y)=24,故此选项错误;
故选:D.
13.D
解:
故答案为D
14.b-2a
解:因为(b+2a)(b-2a)=b2-4a2.
故答案为:b-2a.
15.0
解:根据题意得,x﹣1=0,y+2=0,
解答:x=1,y=﹣2,
∴(2x+y)(2x﹣y)=4x2﹣y2=4﹣4=0,
故答案为:0.
16.(a2-16)
解:根据题意得:文具盒的体积=(a+4)(a-4)×1=(a2-16)(),
故答案是:(a2-16)
17.-8
解:将代入方程组,可得,
①+②,得:3a+3b=12,
∴a+b=4,
①-②,得:a-b=-2,
∴a2-b2=(a+b)(a-b)=4×(-2)=-8,
故答案为:-8.
18.2023
解:由题意知,
当时,,
故答案为:2023.
19.(1)39999;(2)1
解:(1)原式=(200-1)×(200+1)
=2002-12
=40000-1
=39999;
(2)20132﹣(2013+1)×(2013-1)
=20132-20132+1
=1.
20.x2+x-7;-5
解:原式=6x2-6x2+4x-3x+2+x2-9
=x2+x-7,
当x=﹣2时,原式= ,
21.(1);(2)
解:(1)
展开式中不含x的二次项和一次项,
,
解得:,
;
(2)当时,
.
22.(1)a2 b2=(a+b)(a b);(2)①99.96;②x2 6xz+9z2 4y2
解:(1)图甲阴影面积=a2 b2,图乙阴影面积=(a+b)(a b),
∴得到的等式为:a2 b2=(a+b)(a b),
故答案为:a2 b2=(a+b)(a b);
(2)①10.2×9.8
=(10+0.2)×(10 0.2)
=102 0.22
=100 0.04
=99.96;
②
=(x 3z+2y)(x 3z 2y)
=(x 3z)2 (2y)2
=x2 6xz+9z2 4y2.
