第三章圆拔高培优综合试题二2021-2022学年北师大版九年级数学下册(word版含答案)
文档属性
| 名称 | 第三章圆拔高培优综合试题二2021-2022学年北师大版九年级数学下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 373.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 11:04:05 | ||
图片预览



文档简介
北师大版九下 圆拔高培优综合试题一
一.选择题(共10小题)
1.如图,⊙O是正方形ABCD的内切圆,切点分别为E,F,G,H,ED与⊙O相交于点M,则tan∠MFG的值是( )
A. B. C. D.
2.如图,AB是⊙O的直径,∠ACB的平分线交⊙O于点D,连接AD,BD,给出下列四个结论:①∠ACB=90°;②△ABD是等腰直角三角形;③AD2=DE CD;④AC+BC=CD,其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.①②③④
3.已知点P(x0,y0)和直线y=kx+b,求点P到直线y=kx+b的距离d可用公式计算.例如:点(0,1)到直线y=2x+6的距离d==.根据以上材料解决下面问题:如图,⊙C的圆心C的坐标为(1,1),半径为1,直线l的表达式为y=﹣2x+6,P是直线l上的动点,Q是⊙C上的动点,则PQ的最小值是( )
A. B. C. D.2
4.如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的个数有( )
①PB=PD;②的长为π;③∠DBE=45°;④△BCF∽△PCB;⑤CF CP为定值.
A.2个 B.3个 C.4个 D.5个
5.如图,直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙A与直线l:y=x只有一个公共点时,点A的坐标为( )
A.(﹣12,0) B.(﹣13,0) C.(±12,0) D.(±13,0)
6.如图,在圆O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
A.16 B.20 C.18 D.22
7.如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若=,设∠ABC=α,则α所在的范围是( )
A.21.9°<α<22.3° B.22.3°<α<22.7° C.22.7°<α<23.1° D.23.1°<α<23.5°
8.有一张矩形纸片ABCD,已知AB=2,AD=4,上面有一个以AD为直径的半圆,如图甲,将它沿DE折叠,使A点落在BC上,如图乙,这时,半圆还露在外面的部分(阴影部分)的面积是( )
A.π﹣2 B.π+ C.π﹣ D.
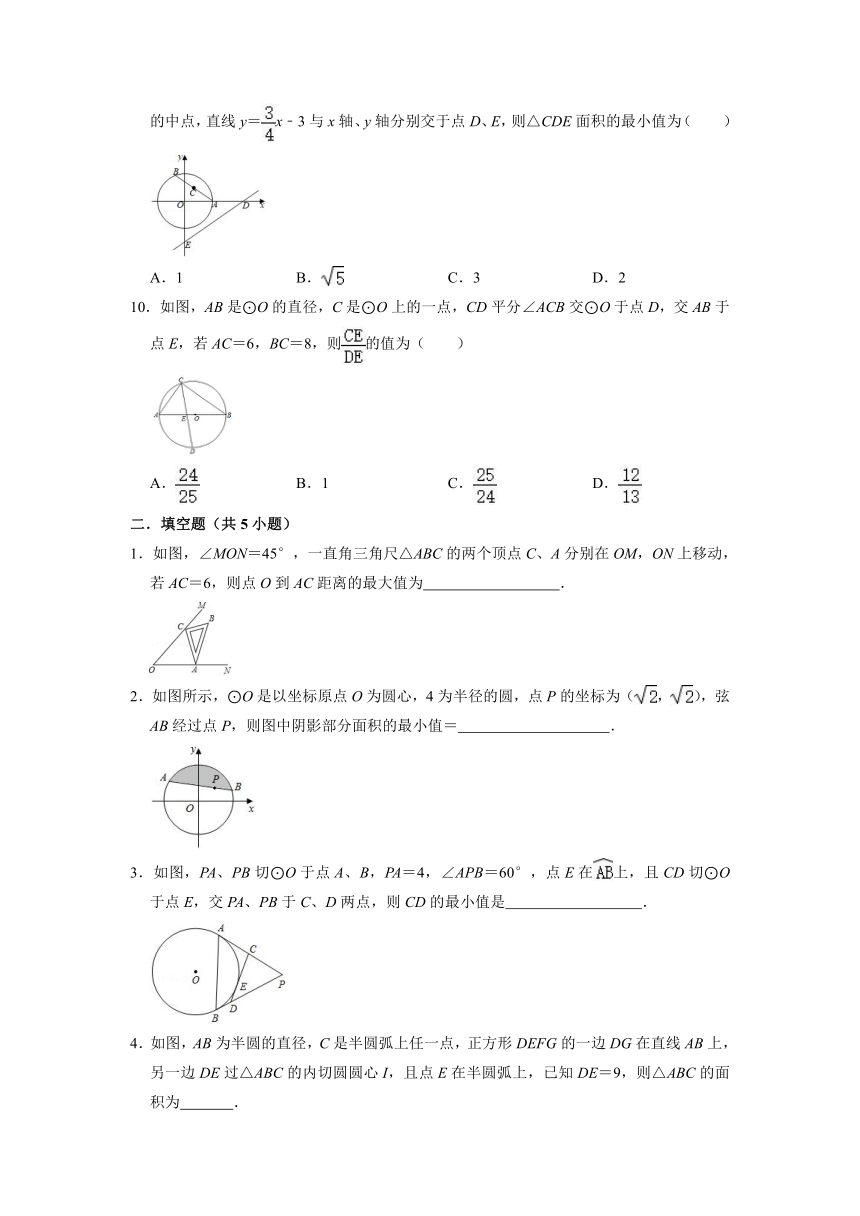
9.如图,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为( )
A.1 B. C.3 D.2
10.如图,AB是⊙O的直径,C是⊙O上的一点,CD平分∠ACB交⊙O于点D,交AB于点E,若AC=6,BC=8,则的值为( )
A. B.1 C. D.
二.填空题(共5小题)
1.如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=6,则点O到AC距离的最大值为 .
2.如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为(,),弦AB经过点P,则图中阴影部分面积的最小值= .
3.如图,PA、PB切⊙O于点A、B,PA=4,∠APB=60°,点E在上,且CD切⊙O于点E,交PA、PB于C、D两点,则CD的最小值是 .
4.如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为 .
5.如图,AB是⊙O的直径,AB=4,过点B作⊙O的切线,C是切线上一点,且BC=2,P是线段OA中点,连接PC交⊙O于点D,过点P作PC的垂线,交切线BC于点E,交⊙O于点F,连接DF交AB于点G,则PE的长为 .
三.解答题(共5小题)
1.如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于D,DE交BC于F,且EF=EC.
(1)求证:EC是⊙O的切线;
(2)求证:△OAC∽△ECF;
(3)若BD=4,BC=8,圆的半径OB=5,求EC的长.
2.如图,已知AB是⊙O的直径,直线AC与⊙O相切于点A,过点B作BD∥OC交⊙O于点D,连接CD并延长交AB的延长线于点E.
(1)求证:CD是⊙O的切线.
(2)求证:DE2=EB EA;
(3)若BE=1,,求线段AD的长度.
3.已知,如图1,在△ABC中,AB=AC,点D是BC边上动点,E是△ABD外接圆⊙O上的点,且,连结DE,BE.
(1)求证:CD=BE;
(2)如图2,当AE∥BC时.
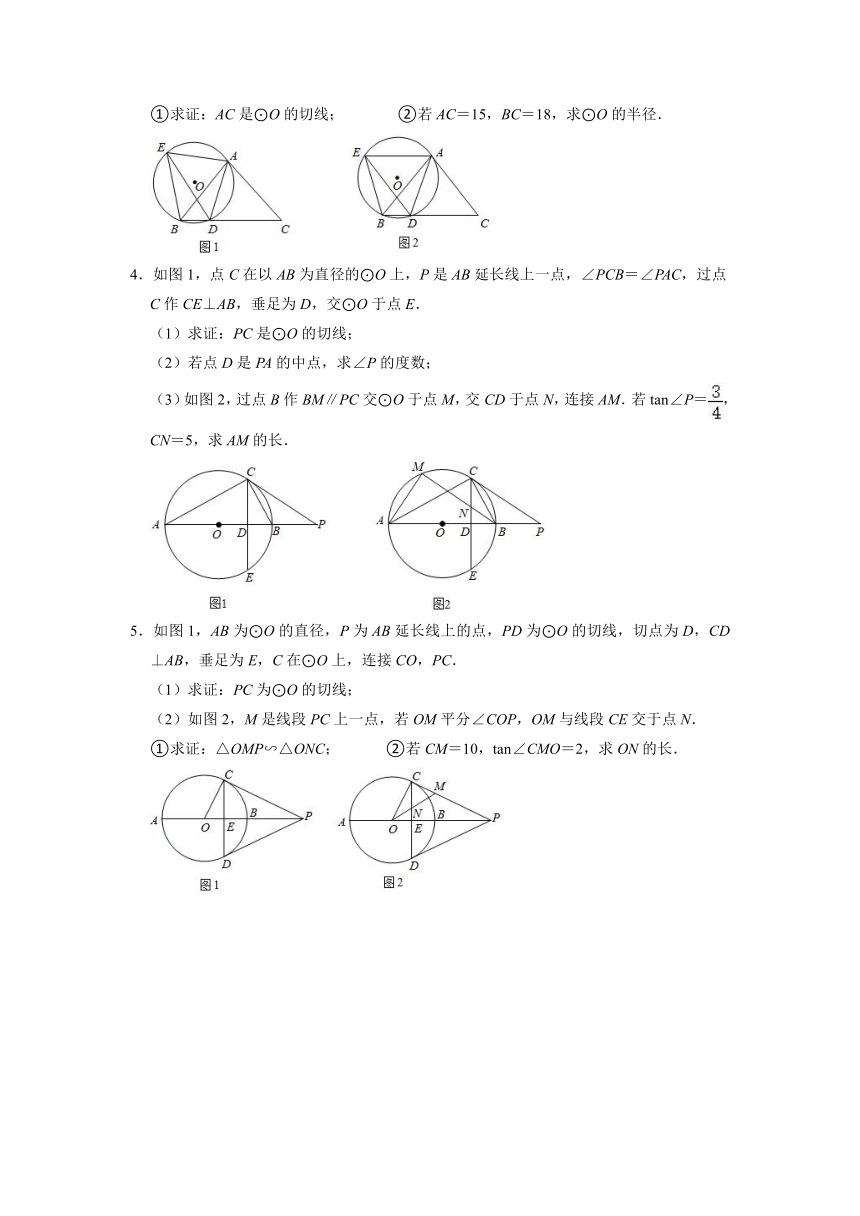
①求证:AC是⊙O的切线; ②若AC=15,BC=18,求⊙O的半径.
4.如图1,点C在以AB为直径的⊙O上,P是AB延长线上一点,∠PCB=∠PAC,过点C作CE⊥AB,垂足为D,交⊙O于点E.
(1)求证:PC是⊙O的切线;
(2)若点D是PA的中点,求∠P的度数;
(3)如图2,过点B作BM∥PC交⊙O于点M,交CD于点N,连接AM.若tan∠P=,CN=5,求AM的长.
5.如图1,AB为⊙O的直径,P为AB延长线上的点,PD为⊙O的切线,切点为D,CD⊥AB,垂足为E,C在⊙O上,连接CO,PC.
(1)求证:PC为⊙O的切线;
(2)如图2,M是线段PC上一点,若OM平分∠COP,OM与线段CE交于点N.
①求证:△OMP∽△ONC; ②若CM=10,tan∠CMO=2,求ON的长.
参考答案
一.选择题(共10小题)
1.B. 2.D. 3.B. 4.B. 5.D.
6.B. 7.B. 8.C. 9.D. 10.A.
二.填空题(共5小题)
1. 3 . 2. . 3. . 4. 81 . 5. .
三.解答题(共5小题)
1.如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于D,DE交BC于F,且EF=EC.
(1)求证:EC是⊙O的切线;
(2)求证:△OAC∽△ECF;
(3)若BD=4,BC=8,圆的半径OB=5,求EC的长.
【解答】(1)证明:∵OC=OB,
∴∠OBC=∠OCB,
∵DE⊥AB,
∴∠OBC+∠DFB=90°,
∵EF=EC,
∴∠ECF=∠EFC=∠DFB,
∴∠OCB+∠ECF=90°,
∴OC⊥CE,
∴EC是⊙O的切线;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠A=90°,∠ABC+∠BFD=90°,
∴∠BFD=∠A,
∴∠A=∠BFD=∠ECF=∠EFC,
∵OA=OC,
∴∠OCA=∠A=∠BFD=∠ECF=∠EFC,
∴△OAC∽△ECF;
(3)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OB=5,
∴AB=10,
∴AC===6,
∵cos∠ABC=,
∴,
∴BF=5,
∴CF=BC﹣BF=3,
∵△OAC∽△ECF,
∴,
∴EC==.
2.如图,已知AB是⊙O的直径,直线AC与⊙O相切于点A,过点B作BD∥OC交⊙O于点D,连接CD并延长交AB的延长线于点E.
(1)求证:CD是⊙O的切线.
(2)求证:DE2=EB EA;
(3)若BE=1,,求线段AD的长度.
【解答】解:(1)∵BD∥OC,
∴∠DBO=∠COA,∠ODB=∠COD,
∵OB=OD,
∴∠DBO=∠ODB,
∴∠COA=∠COD,
在△COA和△COD中,
,
∴△COA≌△COD(SAS),
∴∠CAO=∠CDO,
∵AC是⊙O的切线,
∴∠CAO=90°=∠CDO,
即OD⊥EC,
∵OD是⊙O的半径,
∴EC是⊙O的切线;
(2)∵EC是⊙O的切线,
∴∠ODE=90°,
即∠EDB+∠ODB=90°,
又∴AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
又∵∠ODB=∠OBD,
∴∠EDB=∠EAD,
又∵∠E=∠E,
∴△EBD∽△EDA,
∴=,
即DE2=AE BE;
(3)∵∠ACO+∠COA=90°,
∠BAD+∠OBD=90°,
而∠OBD=∠ODB=∠COD=∠COA,
∴∠ABD+∠BAD=90°,
∴∠BAD=∠ACO,
由△EBD∽△EDA,
∴==tan∠BAD=,
∵BE=1,
∴DE=2,
由DE2=AE BE得,
22=1×AE,
∴AE=4,
∴AB=4﹣1=3,
设BD=a,则AD=2a,由勾股定理得,
BD2+AD2=AB2,
即a2+(2a)2=32,
解得a=,
∴AD=2a=.
2.已知,如图1,在△ABC中,AB=AC,点D是BC边上动点,E是△ABD外接圆⊙O上的点,且,连结DE,BE.
(1)求证:CD=BE;
(2)如图2,当AE∥BC时.
①求证:AC是⊙O的切线;
②若AC=15,BC=18,求⊙O的半径.
【解答】(1)证明:∵,
∴AD=AE,∠ADE=∠ABC=∠AED,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=180°﹣∠ACB﹣∠ABC,∠DAE=180°﹣∠ADE﹣∠AED,
∴∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠BAD,
即:∠EAB=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD;
(2)①证明:过点A作AG⊥DE,垂足为G,
∵O是△ADE的外接圆的圆心,
∴O是△ADE三边垂直平分线的交点,
∵AD=AE,AG⊥DE,
∴AG垂直平分DE,
∴圆心O在AG上,
∵AE∥BC
∴弧AD=弧EB,
∴BE=AD,
∵BE=CD,AE=AD,
∴AE=CD,
∴四边形ACBD为平行四边形,
∴AC∥DE,
∴AG⊥AC,
∴AC是⊙O的切线.
②过点A作AF⊥BC,连接OD,
在等腰三角形△ABC中,AB=AC,
∵AF⊥BC,AC=15,BC=18,
∴BF=FC=,
在Rt△AFC中,,
又∵四边形ACDE为平行四边形,
∴DC=AE=AD,AB=AC=15,
在Rt△ADF中,设AD=x,则DF=x﹣9,
∴AD2=DF2+AF2,
即x2=(x﹣9)2+12,
∴x=.
∴AD=CD=AE=,
又∵∠ABC=∠ADE=∠AED=∠ACB,
∴△ADE∽△ACB,
∴,即,
∴AG=10,
∵DE=AC=15,
∴DG=7.5,
在Rt△ODG和⊙O中,
∵OD2=OG2+DG2,OA=OD,OG=AG﹣OA,
∴OD2=(10﹣OD)2+7.52,
∴,
即△ADE外接圆⊙O半径为.
4.如图1,点C在以AB为直径的⊙O上,P是AB延长线上一点,∠PCB=∠PAC,过点C作CE⊥AB,垂足为D,交⊙O于点E.
(1)求证:PC是⊙O的切线;
(2)若点D是PA的中点,求∠P的度数;
(3)如图2,过点B作BM∥PC交⊙O于点M,交CD于点N,连接AM.若tan∠P=,CN=5,求AM的长.
【解答】(1)证明:连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
即∠OCA+∠BCO=90°,
∵OC=OA,
∴∠OCA=∠PAC,
∴∠PAC+∠BCO=90°,
∵∠PCB=∠PAC,
∴∠PCB+∠BCO=90°,
∴∠OCP=90°,
∵OC是圆的半径,
∴PC是⊙O的切线.
(2)解:∵D是PA的中点,CE⊥AB,
∴AC=CP,∠P=∠PAC,
∵∠PCB=∠PAC=∠P,
∴∠ABC=2∠PAC,
∵AB为⊙O的直径,
∴∠PAC+∠ABC=90°,
∴3∠PAC=90°,
∴∠P=∠PAC=30°.
(3)∵BM∥PC,
∴∠PCB=∠CBM,
∵CE⊥AB,
∴,
∴∠BCE=∠BAC,
∵∠PCB=∠BAC,
∴∠BCE=∠CBM,
∴CN=BN=5,
在Rt△DBN中,
∵BM∥PC,
∴∠DBN=∠P,
∵tan∠DBN=tan∠P=,
∴DN:DB:BN=3:4:5,
∵BN=5,
∴DN=3,BD=4,
∴CD=8,
在Rt△OCD中,设OC=r,则r2﹣(r﹣4)2=82,
解得r=10,
∴AB=2r=20,
在Rt△ABM中,,
∴AM:AB=3:5,
∴AM=12.
5.如图1,AB为⊙O的直径,P为AB延长线上的点,PD为⊙O的切线,切点为D,CD⊥AB,垂足为E,C在⊙O上,连接CO,PC.
(1)求证:PC为⊙O的切线;
(2)如图2,M是线段PC上一点,若OM平分∠COP,OM与线段CE交于点N.
①求证:△OMP∽△ONC;
②若CM=10,tan∠CMO=2,求ON的长.
【解答】证明:(1)连接OD,如图1,
∵PD为⊙O切线,
∴∠ODP=90°,
∵AB⊥CD,且AB为⊙O直径,
∴AB垂直平分CD,
∴PC=PD,
∴∠PCD=∠PDC,
又∵OC=OD,
∴∠OCD=∠ODC,
∴∠OCP=∠OCD+∠PCD=∠ODC+∠PDC=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(2)①∵AB⊥CD,
∴∠CEP=90°,
∴∠ECP+∠MPO=90°,
又∠OCD+∠ECP=90°,
∴∠MPO=∠OCD,
又OM平分∠COP,
∴∠CON=∠MOP,
∴△OMP∽△ONC;
(2)②∵∠CNM=∠CON+∠OCN,
∠CMO=∠CPO+∠MOP,
∴∠CNM=∠CMN,
∴CM=CN=10,
过点C作CG⊥MN于G,
∵tan∠CMO=2,
∴NG=MG=2,CG=4,
在Rt△OCM中,由勾股定理得:OM=,
∴ON=OM﹣MN=10。
一.选择题(共10小题)
1.如图,⊙O是正方形ABCD的内切圆,切点分别为E,F,G,H,ED与⊙O相交于点M,则tan∠MFG的值是( )
A. B. C. D.
2.如图,AB是⊙O的直径,∠ACB的平分线交⊙O于点D,连接AD,BD,给出下列四个结论:①∠ACB=90°;②△ABD是等腰直角三角形;③AD2=DE CD;④AC+BC=CD,其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.①②③④
3.已知点P(x0,y0)和直线y=kx+b,求点P到直线y=kx+b的距离d可用公式计算.例如:点(0,1)到直线y=2x+6的距离d==.根据以上材料解决下面问题:如图,⊙C的圆心C的坐标为(1,1),半径为1,直线l的表达式为y=﹣2x+6,P是直线l上的动点,Q是⊙C上的动点,则PQ的最小值是( )
A. B. C. D.2
4.如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的个数有( )
①PB=PD;②的长为π;③∠DBE=45°;④△BCF∽△PCB;⑤CF CP为定值.
A.2个 B.3个 C.4个 D.5个
5.如图,直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙A与直线l:y=x只有一个公共点时,点A的坐标为( )
A.(﹣12,0) B.(﹣13,0) C.(±12,0) D.(±13,0)
6.如图,在圆O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
A.16 B.20 C.18 D.22
7.如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若=,设∠ABC=α,则α所在的范围是( )
A.21.9°<α<22.3° B.22.3°<α<22.7° C.22.7°<α<23.1° D.23.1°<α<23.5°
8.有一张矩形纸片ABCD,已知AB=2,AD=4,上面有一个以AD为直径的半圆,如图甲,将它沿DE折叠,使A点落在BC上,如图乙,这时,半圆还露在外面的部分(阴影部分)的面积是( )
A.π﹣2 B.π+ C.π﹣ D.
9.如图,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为( )
A.1 B. C.3 D.2
10.如图,AB是⊙O的直径,C是⊙O上的一点,CD平分∠ACB交⊙O于点D,交AB于点E,若AC=6,BC=8,则的值为( )
A. B.1 C. D.
二.填空题(共5小题)
1.如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=6,则点O到AC距离的最大值为 .
2.如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为(,),弦AB经过点P,则图中阴影部分面积的最小值= .
3.如图,PA、PB切⊙O于点A、B,PA=4,∠APB=60°,点E在上,且CD切⊙O于点E,交PA、PB于C、D两点,则CD的最小值是 .
4.如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为 .
5.如图,AB是⊙O的直径,AB=4,过点B作⊙O的切线,C是切线上一点,且BC=2,P是线段OA中点,连接PC交⊙O于点D,过点P作PC的垂线,交切线BC于点E,交⊙O于点F,连接DF交AB于点G,则PE的长为 .
三.解答题(共5小题)
1.如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于D,DE交BC于F,且EF=EC.
(1)求证:EC是⊙O的切线;
(2)求证:△OAC∽△ECF;
(3)若BD=4,BC=8,圆的半径OB=5,求EC的长.
2.如图,已知AB是⊙O的直径,直线AC与⊙O相切于点A,过点B作BD∥OC交⊙O于点D,连接CD并延长交AB的延长线于点E.
(1)求证:CD是⊙O的切线.
(2)求证:DE2=EB EA;
(3)若BE=1,,求线段AD的长度.
3.已知,如图1,在△ABC中,AB=AC,点D是BC边上动点,E是△ABD外接圆⊙O上的点,且,连结DE,BE.
(1)求证:CD=BE;
(2)如图2,当AE∥BC时.
①求证:AC是⊙O的切线; ②若AC=15,BC=18,求⊙O的半径.
4.如图1,点C在以AB为直径的⊙O上,P是AB延长线上一点,∠PCB=∠PAC,过点C作CE⊥AB,垂足为D,交⊙O于点E.
(1)求证:PC是⊙O的切线;
(2)若点D是PA的中点,求∠P的度数;
(3)如图2,过点B作BM∥PC交⊙O于点M,交CD于点N,连接AM.若tan∠P=,CN=5,求AM的长.
5.如图1,AB为⊙O的直径,P为AB延长线上的点,PD为⊙O的切线,切点为D,CD⊥AB,垂足为E,C在⊙O上,连接CO,PC.
(1)求证:PC为⊙O的切线;
(2)如图2,M是线段PC上一点,若OM平分∠COP,OM与线段CE交于点N.
①求证:△OMP∽△ONC; ②若CM=10,tan∠CMO=2,求ON的长.
参考答案
一.选择题(共10小题)
1.B. 2.D. 3.B. 4.B. 5.D.
6.B. 7.B. 8.C. 9.D. 10.A.
二.填空题(共5小题)
1. 3 . 2. . 3. . 4. 81 . 5. .
三.解答题(共5小题)
1.如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于D,DE交BC于F,且EF=EC.
(1)求证:EC是⊙O的切线;
(2)求证:△OAC∽△ECF;
(3)若BD=4,BC=8,圆的半径OB=5,求EC的长.
【解答】(1)证明:∵OC=OB,
∴∠OBC=∠OCB,
∵DE⊥AB,
∴∠OBC+∠DFB=90°,
∵EF=EC,
∴∠ECF=∠EFC=∠DFB,
∴∠OCB+∠ECF=90°,
∴OC⊥CE,
∴EC是⊙O的切线;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠A=90°,∠ABC+∠BFD=90°,
∴∠BFD=∠A,
∴∠A=∠BFD=∠ECF=∠EFC,
∵OA=OC,
∴∠OCA=∠A=∠BFD=∠ECF=∠EFC,
∴△OAC∽△ECF;
(3)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OB=5,
∴AB=10,
∴AC===6,
∵cos∠ABC=,
∴,
∴BF=5,
∴CF=BC﹣BF=3,
∵△OAC∽△ECF,
∴,
∴EC==.
2.如图,已知AB是⊙O的直径,直线AC与⊙O相切于点A,过点B作BD∥OC交⊙O于点D,连接CD并延长交AB的延长线于点E.
(1)求证:CD是⊙O的切线.
(2)求证:DE2=EB EA;
(3)若BE=1,,求线段AD的长度.
【解答】解:(1)∵BD∥OC,
∴∠DBO=∠COA,∠ODB=∠COD,
∵OB=OD,
∴∠DBO=∠ODB,
∴∠COA=∠COD,
在△COA和△COD中,
,
∴△COA≌△COD(SAS),
∴∠CAO=∠CDO,
∵AC是⊙O的切线,
∴∠CAO=90°=∠CDO,
即OD⊥EC,
∵OD是⊙O的半径,
∴EC是⊙O的切线;
(2)∵EC是⊙O的切线,
∴∠ODE=90°,
即∠EDB+∠ODB=90°,
又∴AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
又∵∠ODB=∠OBD,
∴∠EDB=∠EAD,
又∵∠E=∠E,
∴△EBD∽△EDA,
∴=,
即DE2=AE BE;
(3)∵∠ACO+∠COA=90°,
∠BAD+∠OBD=90°,
而∠OBD=∠ODB=∠COD=∠COA,
∴∠ABD+∠BAD=90°,
∴∠BAD=∠ACO,
由△EBD∽△EDA,
∴==tan∠BAD=,
∵BE=1,
∴DE=2,
由DE2=AE BE得,
22=1×AE,
∴AE=4,
∴AB=4﹣1=3,
设BD=a,则AD=2a,由勾股定理得,
BD2+AD2=AB2,
即a2+(2a)2=32,
解得a=,
∴AD=2a=.
2.已知,如图1,在△ABC中,AB=AC,点D是BC边上动点,E是△ABD外接圆⊙O上的点,且,连结DE,BE.
(1)求证:CD=BE;
(2)如图2,当AE∥BC时.
①求证:AC是⊙O的切线;
②若AC=15,BC=18,求⊙O的半径.
【解答】(1)证明:∵,
∴AD=AE,∠ADE=∠ABC=∠AED,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=180°﹣∠ACB﹣∠ABC,∠DAE=180°﹣∠ADE﹣∠AED,
∴∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠BAD,
即:∠EAB=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD;
(2)①证明:过点A作AG⊥DE,垂足为G,
∵O是△ADE的外接圆的圆心,
∴O是△ADE三边垂直平分线的交点,
∵AD=AE,AG⊥DE,
∴AG垂直平分DE,
∴圆心O在AG上,
∵AE∥BC
∴弧AD=弧EB,
∴BE=AD,
∵BE=CD,AE=AD,
∴AE=CD,
∴四边形ACBD为平行四边形,
∴AC∥DE,
∴AG⊥AC,
∴AC是⊙O的切线.
②过点A作AF⊥BC,连接OD,
在等腰三角形△ABC中,AB=AC,
∵AF⊥BC,AC=15,BC=18,
∴BF=FC=,
在Rt△AFC中,,
又∵四边形ACDE为平行四边形,
∴DC=AE=AD,AB=AC=15,
在Rt△ADF中,设AD=x,则DF=x﹣9,
∴AD2=DF2+AF2,
即x2=(x﹣9)2+12,
∴x=.
∴AD=CD=AE=,
又∵∠ABC=∠ADE=∠AED=∠ACB,
∴△ADE∽△ACB,
∴,即,
∴AG=10,
∵DE=AC=15,
∴DG=7.5,
在Rt△ODG和⊙O中,
∵OD2=OG2+DG2,OA=OD,OG=AG﹣OA,
∴OD2=(10﹣OD)2+7.52,
∴,
即△ADE外接圆⊙O半径为.
4.如图1,点C在以AB为直径的⊙O上,P是AB延长线上一点,∠PCB=∠PAC,过点C作CE⊥AB,垂足为D,交⊙O于点E.
(1)求证:PC是⊙O的切线;
(2)若点D是PA的中点,求∠P的度数;
(3)如图2,过点B作BM∥PC交⊙O于点M,交CD于点N,连接AM.若tan∠P=,CN=5,求AM的长.
【解答】(1)证明:连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
即∠OCA+∠BCO=90°,
∵OC=OA,
∴∠OCA=∠PAC,
∴∠PAC+∠BCO=90°,
∵∠PCB=∠PAC,
∴∠PCB+∠BCO=90°,
∴∠OCP=90°,
∵OC是圆的半径,
∴PC是⊙O的切线.
(2)解:∵D是PA的中点,CE⊥AB,
∴AC=CP,∠P=∠PAC,
∵∠PCB=∠PAC=∠P,
∴∠ABC=2∠PAC,
∵AB为⊙O的直径,
∴∠PAC+∠ABC=90°,
∴3∠PAC=90°,
∴∠P=∠PAC=30°.
(3)∵BM∥PC,
∴∠PCB=∠CBM,
∵CE⊥AB,
∴,
∴∠BCE=∠BAC,
∵∠PCB=∠BAC,
∴∠BCE=∠CBM,
∴CN=BN=5,
在Rt△DBN中,
∵BM∥PC,
∴∠DBN=∠P,
∵tan∠DBN=tan∠P=,
∴DN:DB:BN=3:4:5,
∵BN=5,
∴DN=3,BD=4,
∴CD=8,
在Rt△OCD中,设OC=r,则r2﹣(r﹣4)2=82,
解得r=10,
∴AB=2r=20,
在Rt△ABM中,,
∴AM:AB=3:5,
∴AM=12.
5.如图1,AB为⊙O的直径,P为AB延长线上的点,PD为⊙O的切线,切点为D,CD⊥AB,垂足为E,C在⊙O上,连接CO,PC.
(1)求证:PC为⊙O的切线;
(2)如图2,M是线段PC上一点,若OM平分∠COP,OM与线段CE交于点N.
①求证:△OMP∽△ONC;
②若CM=10,tan∠CMO=2,求ON的长.
【解答】证明:(1)连接OD,如图1,
∵PD为⊙O切线,
∴∠ODP=90°,
∵AB⊥CD,且AB为⊙O直径,
∴AB垂直平分CD,
∴PC=PD,
∴∠PCD=∠PDC,
又∵OC=OD,
∴∠OCD=∠ODC,
∴∠OCP=∠OCD+∠PCD=∠ODC+∠PDC=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(2)①∵AB⊥CD,
∴∠CEP=90°,
∴∠ECP+∠MPO=90°,
又∠OCD+∠ECP=90°,
∴∠MPO=∠OCD,
又OM平分∠COP,
∴∠CON=∠MOP,
∴△OMP∽△ONC;
(2)②∵∠CNM=∠CON+∠OCN,
∠CMO=∠CPO+∠MOP,
∴∠CNM=∠CMN,
∴CM=CN=10,
过点C作CG⊥MN于G,
∵tan∠CMO=2,
∴NG=MG=2,CG=4,
在Rt△OCM中,由勾股定理得:OM=,
∴ON=OM﹣MN=10。
