第三章圆拔高培优综合试题一2020-2021学年北师大版九年级数学下册(word版含答案)
文档属性
| 名称 | 第三章圆拔高培优综合试题一2020-2021学年北师大版九年级数学下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 457.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 11:05:35 | ||
图片预览




文档简介
北师大版九下 圆拔高培优综合试题一
一.选择题(共10小题)
1.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4 B. C. D.
2.如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
A.2周 B.3周 C.4周 D.5周
3.如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
A.0<x≤ B.﹣≤x≤ C.﹣1≤x≤1 D.x>
4.如图所示,在直角坐标系中,A点坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为( )
A.(﹣4,0) B.(﹣2,0) C.(﹣4,0)或(﹣2,0) D.(﹣3,0)
5.如图,已知⊙O的弦AB、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=cm,则PE的长为( )
A.4cm B.3cm C.5cm D.cm
6.如图,⊙O的直径为10cm,弦AB为8cm,P是弦AB上一点,若OP的长为整数,则满足条件的点P有( )
A.2个 B.3个 C.4个 D.5个
7.如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④.其中一定成立的是( )
A.①②③ B.②③④ C.①③④ D.①②④
8.如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是:①PB=PD;②的长为π;③∠DBE=45°;④当P为中点时,EC=EF;⑤∠DFB=∠CBP.其中正确的个数为( )
A.5 B.4 C.3 D.2
9.如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为上一点(点P不与点B,C重合),连接AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,的值始终等于.则下列说法正确的是( )
A.①,②都对 B.①对,②错 C.①错,②对 D.①,②都错
10.如图,直线y=x+3与x轴、y轴分别交于A,B两点,点P是以C(1,0)为圆心,1为半径的圆上任意一点,连接PA,PB,则△PAB面积的最小值是( )
A.5 B.10 C.15 D.20
二.填空题(共5小题)
1.如图,⊙O内切于正方形ABCD,边AD,DC上两点E,F,且EF是⊙O的切线,当△BEF的面积为时,则⊙O的半径r是 .
2.如图,在平面直角坐标系中,半径为3的⊙O与y轴的负半轴交于点A,点B是⊙O上移动点,点C为弦AB的中点,直线与x轴、y轴分别相交于点D、E,则△CDE面积的最小值为 .
3.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
4.如图,在矩形ABCD中,AB=4,BC=3,E,F分别为AB,CD边的中点.动点P从点E出发沿EA向点A运动,同时,动点Q从点F出发沿FC向点C运动,连接PQ,过点B作BH⊥PQ于点H,连接DH.若点P的速度是点Q的速度的2倍,在点P从点E运动至点A的过程中,线段PQ长度的最大值为 ,线段DH长度的最小值为 .
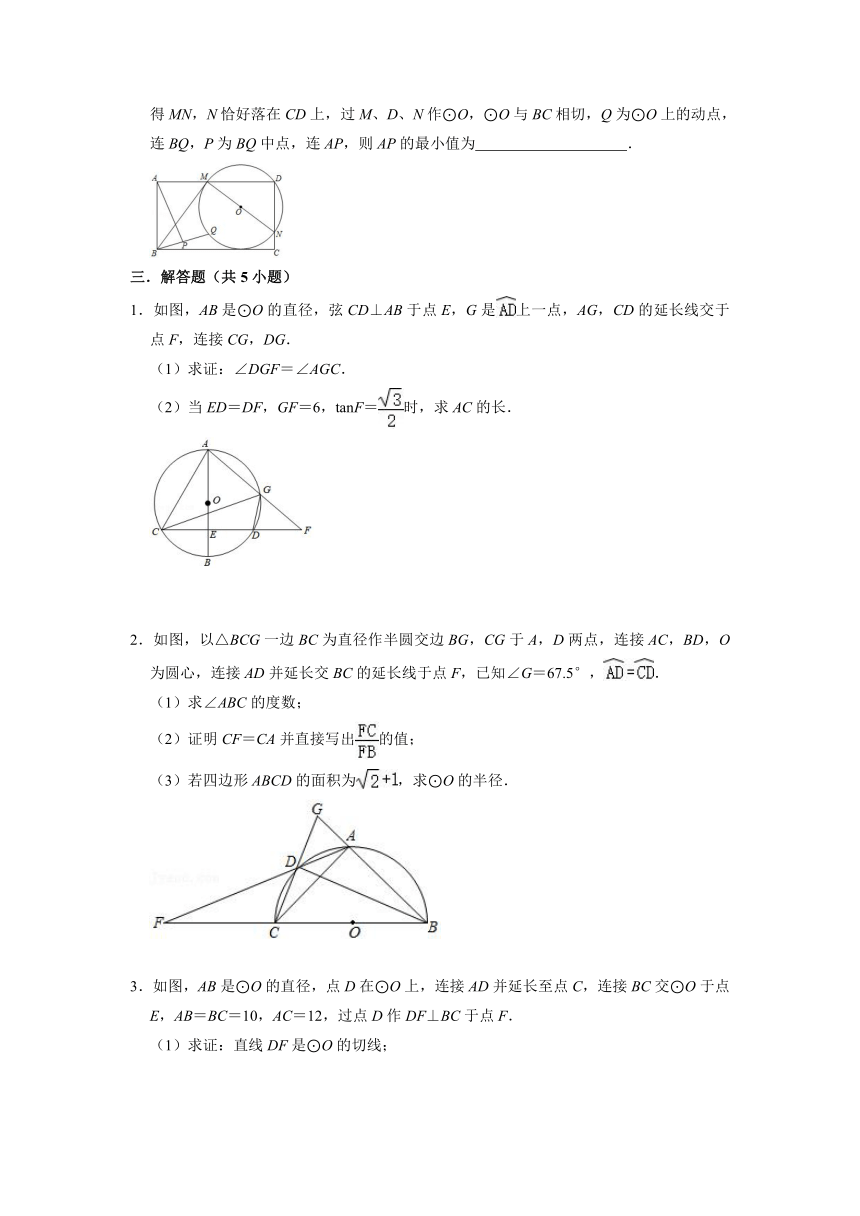
5.矩形ABCD的边AB=4,边AD上有一点M,连接BM,将MB绕M点逆时针旋转90°得MN,N恰好落在CD上,过M、D、N作⊙O,⊙O与BC相切,Q为⊙O上的动点,连BQ,P为BQ中点,连AP,则AP的最小值为 .
三.解答题(共5小题)
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,CD的延长线交于点F,连接CG,DG.
(1)求证:∠DGF=∠AGC.
(2)当ED=DF,GF=6,tanF=时,求AC的长.
2.如图,以△BCG一边BC为直径作半圆交边BG,CG于A,D两点,连接AC,BD,O为圆心,连接AD并延长交BC的延长线于点F,已知∠G=67.5°,.
(1)求∠ABC的度数;
(2)证明CF=CA并直接写出的值;
(3)若四边形ABCD的面积为,求⊙O的半径.
3.如图,AB是⊙O的直径,点D在⊙O上,连接AD并延长至点C,连接BC交⊙O于点E,AB=BC=10,AC=12,过点D作DF⊥BC于点F.
(1)求证:直线DF是⊙O的切线;
(2)连接DE,设△CDE的面积为S1,四边形ADEB的面积为S2,求的值;
(3)点P在上,且的长为,点Q为线段BD上一动点,连接PQ,求的最小值.
4.如图①,Rt△ABC中,CA=CB,∠ACB=90°,经过顶点B,C作⊙O,分别交边AB,AC于点D,E,连接DE,DC.
(1)求证:AD=ED.
(2)当AE=4,CE=2时,求⊙O的半径.
(3)设=x,tan∠DCB=y.
①求y关于x的函数表达式; ②如图②,连接OE,OD,若=,求y的值.
5.如图,在△ABC的边BC上取一点O,以O为圆心,OC为半径画⊙O与边AB相切于点D,AC=AD,连接OA交⊙O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是⊙O切线;
(2)若AC=8,sin∠CAB=,求⊙O半径;
(3)若F是AB中点,求证:CE CF=OE BC.
参考答案
一.选择题(共10小题)
1.B. 2.C. 3.A. 4.D. 5.A.
6.D. 7.D. 8.C. 9.A. 10.A.
二.填空题(共5小题)
1. . 2. . 3. . 4. ﹣ . 5. .
三.解答题(共5小题)
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,CD的延长线交于点F,连接CG,DG.
(1)求证:∠DGF=∠AGC.
(2)当ED=DF,GF=6,tanF=时,求AC的长.
【解答】(1)证明:∵四边形ACDG是⊙O的内接四边形,
∴∠ACD+∠AGD=180°,
∵∠AGD+∠DGF=180°,
∴∠ACD=∠DGF,
∵CD⊥AB,AB为直径,
∴=,
∴∠AGC=∠ACD,
∴∠DGF=∠AGC.
(2)∵∠DGF=∠ACD,∠F=∠F,
∴△FDG∽△FAC,
∴=,
∴FD FC=FG FA,
∵CD⊥AB,
∴tanF==,
∵ED=DF,
∴EF=2DE,
∵==,
∴==,
∴∠ACD=60°,
∴∠CAE=30°,
∴AC=2CE,
设CE=DE=DF=x,则AE=x,AC=2x,FC=3x,
在Rt△AEF中,由勾股定理得AF==x,
∵FD FC=FA FG,
∴x 3x=6x,
解得x=0(舍)或x=2,
∴AC=2x=4.
2.如图,以△BCG一边BC为直径作半圆交边BG,CG于A,D两点,连接AC,BD,O为圆心,连接AD并延长交BC的延长线于点F,已知∠G=67.5°,.
(1)求∠ABC的度数;
(2)证明CF=CA并直接写出的值;
(3)若四边形ABCD的面积为,求⊙O的半径.
【解答】(1)解:∵BC是直径,
∴∠BDC=∠BDG=90°,
∵∠G=67.5°,
∴∠GBD=90°﹣67.5°=22.5°,
∵=,
∴∠ABD=∠DBC=22.5°,
∴∠ABC=∠ABD+∠DBC=45°.
(2)证明:∵BC是直径,
∴∠CAB=90°,
∵∠ABC=45°,
∴∠ACB=∠ABC=45°,
∵∠CAD=∠CBD=22.5°∠ACB=∠F+∠CAD,
∴∠F=∠CAD=22.5°,
∴CF=CA,
设CF=CA=AB=m,则BC=m,BF=m+m,
∴==﹣1.
(3)解:如图,连接OD,过点D作DE⊥BG于点E,DF⊥BC于点F.
∵∠DBE=∠DBF=22.5°,DE⊥BE,DF⊥BF,
∴DE=DF,
∵=,
∴AD=CD,
∵∠DFC=∠DEA=90°,
∴Rt△DEA≌△DFC(HL),
∴S△ADE=S△CDF,
∴S四边形ABCD=S四边形DEBF,
∵DE=DF,BD=BD,∠BED=∠BFD,
∴△BDE≌△BDF(HL),
∴S四边形ABCD=2S△BDF,
设OD=OB=r,
∵∠ODB=∠OBD=22.5°,
∴∠DOF=∠ODB+∠OBD=45°,
∴∠FDO=∠DOF=45°,
∴DF=OF=r,
∵四边形ABCD的面积为,
∴2××(r+r)×r=+1,
∴r=(负根已经舍弃),
∴⊙O的半径为.
3.如图,AB是⊙O的直径,点D在⊙O上,连接AD并延长至点C,连接BC交⊙O于点E,AB=BC=10,AC=12,过点D作DF⊥BC于点F.
(1)求证:直线DF是⊙O的切线;
(2)连接DE,设△CDE的面积为S1,四边形ADEB的面积为S2,求的值;
(3)点P在上,且的长为,点Q为线段BD上一动点,连接PQ,求的最小值.
【解答】(1)证明:连接OD,
∵AO=OD,
∴∠OAD=∠ODA,
∵AB=BC,
∴∠OAD=∠C.
∴∠ODA=∠C,
∴OD∥BC,
∵DF⊥BC,
∴DF⊥OD,
∵OD是⊙O的半径,
∴直线DF是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=BC,
∴AD=DC=6,
∵四边形ADEB是⊙O的内接四边形,
∴∠ADE+∠ABE=180°,
∵∠ADE+∠CDE=180°,
∴∠CDE=∠ABC,
∵∠C=∠C,
∴△CDE∽△CBA,
∴=,
∴;
(3)如图,过点Q作QG⊥AB于点G,
∵sin∠ABD=,
∴QG=BQ,
∴PQ+BQ=PQ+QG,
∴当P,Q,G三点共线时,PQ+BQ有最小值为PG,
∵的弧长为π,
∴,
∴∠POB=60°,
∴PG=OP sin60°=,
∴PQ+BQ的最小值为.
4.如图①,Rt△ABC中,CA=CB,∠ACB=90°,经过顶点B,C作⊙O,分别交边AB,AC于点D,E,连接DE,DC.
(1)求证:AD=ED.
(2)当AE=4,CE=2时,求⊙O的半径.
(3)设=x,tan∠DCB=y.
①求y关于x的函数表达式;
②如图②,连接OE,OD,若=,求y的值.
【解答】(1)证明:∵∠ACB=90°,且⊙O经过B、C、E,
∴直线BE为⊙O的直径,
∴∠BDE=90°,
∴∠CBD+∠CED=180°,
∵∠AED+∠CED=180°,
∴∠AED=∠CBD,
∵CA=CB,
∴∠CAD=∠CBA,
∴∠DEA=∠DAE,
∴AD=ED.
(2)解:∵∠EDA=∠ACB=90°,∠DAE=∠CBA=45°,
∴△ADE∽△CAB,
∴AE=4,AD=DE,
∴AD=DE==2,CA=AE+CE=2+4=6,且,
即,
∴AB=6,
∴DB=AB﹣AD=4,
∴BE===2,
∴⊙O的半径为.
(3)①∵tan∠DCB=y,
∴,,
∴sin∠DCB= sin∠CBD=,cos∠BCD=,
∴tan∠DCB===y,
设EC=m,
∴AE=mx,
∴BC=m+mx=m(1+x),BD=BC﹣AD,AD=AE,
∴BD=m(1+x)﹣mx=m(1+),
∴∠CED=45°,
∴cos∠CED=﹣=,
∴CD2=m2+m2x2+m2x,
∴y===,
②设CE=n,AE=nx,
∴DE=,AC=n(1+x)=BC,
∴S△ABC=AC BC=n2(1+x)2,BE===n,
∴OE=BE=且△OED为等腰三角形,
∴O点到DE的距离为:==n,
∴S△OED=×nx n=n2,
∵=,
∴=,
∵x>0,
∴x=3,
∴y==.
5.如图,在△ABC的边BC上取一点O,以O为圆心,OC为半径画⊙O与边AB相切于点D,AC=AD,连接OA交⊙O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是⊙O切线;
(2)若AC=8,sin∠CAB=,求⊙O半径;
(3)若F是AB中点,求证:CE CF=OE BC.
【解答】(1)证明:连OD,
在△AOC和△AOD中,
,
∴△AOC△AOD(SSS),
∴∠ACO=∠ADO,
∵AB与⊙O相切,
∴OD⊥AB,
∴∠ADO=90°,
∴∠ACO=90°,
∴OC⊥AC,
∵OC为半径,
∴AC是⊙O切线;
(2)解:连接OD,
设BC=3x,则AB=5x,
∵AC2+BC2=AB2,
∴82+(3x)2=(5x)2,
∴x=2,
∴BC=6,
设OD=a,则OB=6﹣a,
∵sin∠CAB=,
∴sin∠OBD=,
∴,
∴a=,
∴OD=,
∴⊙O半径为;
(3)证明:∵F为AB的中点,∠ACB=90°,
∴AF=CF=BF,
∴∠FCB=∠FBC,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OEC=∠FBC,
∴△OCE∽△FCB,
∴,
∴,
∴CE CF=OE BC.
一.选择题(共10小题)
1.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4 B. C. D.
2.如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
A.2周 B.3周 C.4周 D.5周
3.如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
A.0<x≤ B.﹣≤x≤ C.﹣1≤x≤1 D.x>
4.如图所示,在直角坐标系中,A点坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为( )
A.(﹣4,0) B.(﹣2,0) C.(﹣4,0)或(﹣2,0) D.(﹣3,0)
5.如图,已知⊙O的弦AB、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=cm,则PE的长为( )
A.4cm B.3cm C.5cm D.cm
6.如图,⊙O的直径为10cm,弦AB为8cm,P是弦AB上一点,若OP的长为整数,则满足条件的点P有( )
A.2个 B.3个 C.4个 D.5个
7.如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④.其中一定成立的是( )
A.①②③ B.②③④ C.①③④ D.①②④
8.如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是:①PB=PD;②的长为π;③∠DBE=45°;④当P为中点时,EC=EF;⑤∠DFB=∠CBP.其中正确的个数为( )
A.5 B.4 C.3 D.2
9.如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为上一点(点P不与点B,C重合),连接AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,的值始终等于.则下列说法正确的是( )
A.①,②都对 B.①对,②错 C.①错,②对 D.①,②都错
10.如图,直线y=x+3与x轴、y轴分别交于A,B两点,点P是以C(1,0)为圆心,1为半径的圆上任意一点,连接PA,PB,则△PAB面积的最小值是( )
A.5 B.10 C.15 D.20
二.填空题(共5小题)
1.如图,⊙O内切于正方形ABCD,边AD,DC上两点E,F,且EF是⊙O的切线,当△BEF的面积为时,则⊙O的半径r是 .
2.如图,在平面直角坐标系中,半径为3的⊙O与y轴的负半轴交于点A,点B是⊙O上移动点,点C为弦AB的中点,直线与x轴、y轴分别相交于点D、E,则△CDE面积的最小值为 .
3.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
4.如图,在矩形ABCD中,AB=4,BC=3,E,F分别为AB,CD边的中点.动点P从点E出发沿EA向点A运动,同时,动点Q从点F出发沿FC向点C运动,连接PQ,过点B作BH⊥PQ于点H,连接DH.若点P的速度是点Q的速度的2倍,在点P从点E运动至点A的过程中,线段PQ长度的最大值为 ,线段DH长度的最小值为 .
5.矩形ABCD的边AB=4,边AD上有一点M,连接BM,将MB绕M点逆时针旋转90°得MN,N恰好落在CD上,过M、D、N作⊙O,⊙O与BC相切,Q为⊙O上的动点,连BQ,P为BQ中点,连AP,则AP的最小值为 .
三.解答题(共5小题)
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,CD的延长线交于点F,连接CG,DG.
(1)求证:∠DGF=∠AGC.
(2)当ED=DF,GF=6,tanF=时,求AC的长.
2.如图,以△BCG一边BC为直径作半圆交边BG,CG于A,D两点,连接AC,BD,O为圆心,连接AD并延长交BC的延长线于点F,已知∠G=67.5°,.
(1)求∠ABC的度数;
(2)证明CF=CA并直接写出的值;
(3)若四边形ABCD的面积为,求⊙O的半径.
3.如图,AB是⊙O的直径,点D在⊙O上,连接AD并延长至点C,连接BC交⊙O于点E,AB=BC=10,AC=12,过点D作DF⊥BC于点F.
(1)求证:直线DF是⊙O的切线;
(2)连接DE,设△CDE的面积为S1,四边形ADEB的面积为S2,求的值;
(3)点P在上,且的长为,点Q为线段BD上一动点,连接PQ,求的最小值.
4.如图①,Rt△ABC中,CA=CB,∠ACB=90°,经过顶点B,C作⊙O,分别交边AB,AC于点D,E,连接DE,DC.
(1)求证:AD=ED.
(2)当AE=4,CE=2时,求⊙O的半径.
(3)设=x,tan∠DCB=y.
①求y关于x的函数表达式; ②如图②,连接OE,OD,若=,求y的值.
5.如图,在△ABC的边BC上取一点O,以O为圆心,OC为半径画⊙O与边AB相切于点D,AC=AD,连接OA交⊙O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是⊙O切线;
(2)若AC=8,sin∠CAB=,求⊙O半径;
(3)若F是AB中点,求证:CE CF=OE BC.
参考答案
一.选择题(共10小题)
1.B. 2.C. 3.A. 4.D. 5.A.
6.D. 7.D. 8.C. 9.A. 10.A.
二.填空题(共5小题)
1. . 2. . 3. . 4. ﹣ . 5. .
三.解答题(共5小题)
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,CD的延长线交于点F,连接CG,DG.
(1)求证:∠DGF=∠AGC.
(2)当ED=DF,GF=6,tanF=时,求AC的长.
【解答】(1)证明:∵四边形ACDG是⊙O的内接四边形,
∴∠ACD+∠AGD=180°,
∵∠AGD+∠DGF=180°,
∴∠ACD=∠DGF,
∵CD⊥AB,AB为直径,
∴=,
∴∠AGC=∠ACD,
∴∠DGF=∠AGC.
(2)∵∠DGF=∠ACD,∠F=∠F,
∴△FDG∽△FAC,
∴=,
∴FD FC=FG FA,
∵CD⊥AB,
∴tanF==,
∵ED=DF,
∴EF=2DE,
∵==,
∴==,
∴∠ACD=60°,
∴∠CAE=30°,
∴AC=2CE,
设CE=DE=DF=x,则AE=x,AC=2x,FC=3x,
在Rt△AEF中,由勾股定理得AF==x,
∵FD FC=FA FG,
∴x 3x=6x,
解得x=0(舍)或x=2,
∴AC=2x=4.
2.如图,以△BCG一边BC为直径作半圆交边BG,CG于A,D两点,连接AC,BD,O为圆心,连接AD并延长交BC的延长线于点F,已知∠G=67.5°,.
(1)求∠ABC的度数;
(2)证明CF=CA并直接写出的值;
(3)若四边形ABCD的面积为,求⊙O的半径.
【解答】(1)解:∵BC是直径,
∴∠BDC=∠BDG=90°,
∵∠G=67.5°,
∴∠GBD=90°﹣67.5°=22.5°,
∵=,
∴∠ABD=∠DBC=22.5°,
∴∠ABC=∠ABD+∠DBC=45°.
(2)证明:∵BC是直径,
∴∠CAB=90°,
∵∠ABC=45°,
∴∠ACB=∠ABC=45°,
∵∠CAD=∠CBD=22.5°∠ACB=∠F+∠CAD,
∴∠F=∠CAD=22.5°,
∴CF=CA,
设CF=CA=AB=m,则BC=m,BF=m+m,
∴==﹣1.
(3)解:如图,连接OD,过点D作DE⊥BG于点E,DF⊥BC于点F.
∵∠DBE=∠DBF=22.5°,DE⊥BE,DF⊥BF,
∴DE=DF,
∵=,
∴AD=CD,
∵∠DFC=∠DEA=90°,
∴Rt△DEA≌△DFC(HL),
∴S△ADE=S△CDF,
∴S四边形ABCD=S四边形DEBF,
∵DE=DF,BD=BD,∠BED=∠BFD,
∴△BDE≌△BDF(HL),
∴S四边形ABCD=2S△BDF,
设OD=OB=r,
∵∠ODB=∠OBD=22.5°,
∴∠DOF=∠ODB+∠OBD=45°,
∴∠FDO=∠DOF=45°,
∴DF=OF=r,
∵四边形ABCD的面积为,
∴2××(r+r)×r=+1,
∴r=(负根已经舍弃),
∴⊙O的半径为.
3.如图,AB是⊙O的直径,点D在⊙O上,连接AD并延长至点C,连接BC交⊙O于点E,AB=BC=10,AC=12,过点D作DF⊥BC于点F.
(1)求证:直线DF是⊙O的切线;
(2)连接DE,设△CDE的面积为S1,四边形ADEB的面积为S2,求的值;
(3)点P在上,且的长为,点Q为线段BD上一动点,连接PQ,求的最小值.
【解答】(1)证明:连接OD,
∵AO=OD,
∴∠OAD=∠ODA,
∵AB=BC,
∴∠OAD=∠C.
∴∠ODA=∠C,
∴OD∥BC,
∵DF⊥BC,
∴DF⊥OD,
∵OD是⊙O的半径,
∴直线DF是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=BC,
∴AD=DC=6,
∵四边形ADEB是⊙O的内接四边形,
∴∠ADE+∠ABE=180°,
∵∠ADE+∠CDE=180°,
∴∠CDE=∠ABC,
∵∠C=∠C,
∴△CDE∽△CBA,
∴=,
∴;
(3)如图,过点Q作QG⊥AB于点G,
∵sin∠ABD=,
∴QG=BQ,
∴PQ+BQ=PQ+QG,
∴当P,Q,G三点共线时,PQ+BQ有最小值为PG,
∵的弧长为π,
∴,
∴∠POB=60°,
∴PG=OP sin60°=,
∴PQ+BQ的最小值为.
4.如图①,Rt△ABC中,CA=CB,∠ACB=90°,经过顶点B,C作⊙O,分别交边AB,AC于点D,E,连接DE,DC.
(1)求证:AD=ED.
(2)当AE=4,CE=2时,求⊙O的半径.
(3)设=x,tan∠DCB=y.
①求y关于x的函数表达式;
②如图②,连接OE,OD,若=,求y的值.
【解答】(1)证明:∵∠ACB=90°,且⊙O经过B、C、E,
∴直线BE为⊙O的直径,
∴∠BDE=90°,
∴∠CBD+∠CED=180°,
∵∠AED+∠CED=180°,
∴∠AED=∠CBD,
∵CA=CB,
∴∠CAD=∠CBA,
∴∠DEA=∠DAE,
∴AD=ED.
(2)解:∵∠EDA=∠ACB=90°,∠DAE=∠CBA=45°,
∴△ADE∽△CAB,
∴AE=4,AD=DE,
∴AD=DE==2,CA=AE+CE=2+4=6,且,
即,
∴AB=6,
∴DB=AB﹣AD=4,
∴BE===2,
∴⊙O的半径为.
(3)①∵tan∠DCB=y,
∴,,
∴sin∠DCB= sin∠CBD=,cos∠BCD=,
∴tan∠DCB===y,
设EC=m,
∴AE=mx,
∴BC=m+mx=m(1+x),BD=BC﹣AD,AD=AE,
∴BD=m(1+x)﹣mx=m(1+),
∴∠CED=45°,
∴cos∠CED=﹣=,
∴CD2=m2+m2x2+m2x,
∴y===,
②设CE=n,AE=nx,
∴DE=,AC=n(1+x)=BC,
∴S△ABC=AC BC=n2(1+x)2,BE===n,
∴OE=BE=且△OED为等腰三角形,
∴O点到DE的距离为:==n,
∴S△OED=×nx n=n2,
∵=,
∴=,
∵x>0,
∴x=3,
∴y==.
5.如图,在△ABC的边BC上取一点O,以O为圆心,OC为半径画⊙O与边AB相切于点D,AC=AD,连接OA交⊙O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是⊙O切线;
(2)若AC=8,sin∠CAB=,求⊙O半径;
(3)若F是AB中点,求证:CE CF=OE BC.
【解答】(1)证明:连OD,
在△AOC和△AOD中,
,
∴△AOC△AOD(SSS),
∴∠ACO=∠ADO,
∵AB与⊙O相切,
∴OD⊥AB,
∴∠ADO=90°,
∴∠ACO=90°,
∴OC⊥AC,
∵OC为半径,
∴AC是⊙O切线;
(2)解:连接OD,
设BC=3x,则AB=5x,
∵AC2+BC2=AB2,
∴82+(3x)2=(5x)2,
∴x=2,
∴BC=6,
设OD=a,则OB=6﹣a,
∵sin∠CAB=,
∴sin∠OBD=,
∴,
∴a=,
∴OD=,
∴⊙O半径为;
(3)证明:∵F为AB的中点,∠ACB=90°,
∴AF=CF=BF,
∴∠FCB=∠FBC,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OEC=∠FBC,
∴△OCE∽△FCB,
∴,
∴,
∴CE CF=OE BC.
