冀教版七年级数学上册2.7.1角的和与差 教案
文档属性
| 名称 | 冀教版七年级数学上册2.7.1角的和与差 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 00:00:00 | ||
图片预览

文档简介
2.7.1角的和与差
年级 七 学科 数学 主题 2.7.1角的和与差 主备教师
课型 新授课 课时 1 时间 40分钟 导学教师
教学目标 (1)结合具体图形,了解两个角的和与差的意义.会进行角的和差运算,知道如何进位或借位. (2)了解角平分线的意义及其简单应用,了角两角互余、两角互补的意义,会正确表示一个角的余角或补角,能熟练的求出一个角的余角或补角.通过探究,了解“同角(等角)的余角相等“同角(等角)的补角相等”.
教学 重、难点 重点:1、角的和与差、角平分线及其意义. 2、互余、互补的概念及其性质. 难点:两角互余、两角互补的本质特征,互余、互补的性质.
导学方法 自主学习,合作交流
导学步骤 导学行为(师生活动) 设计意图 导学教师复备
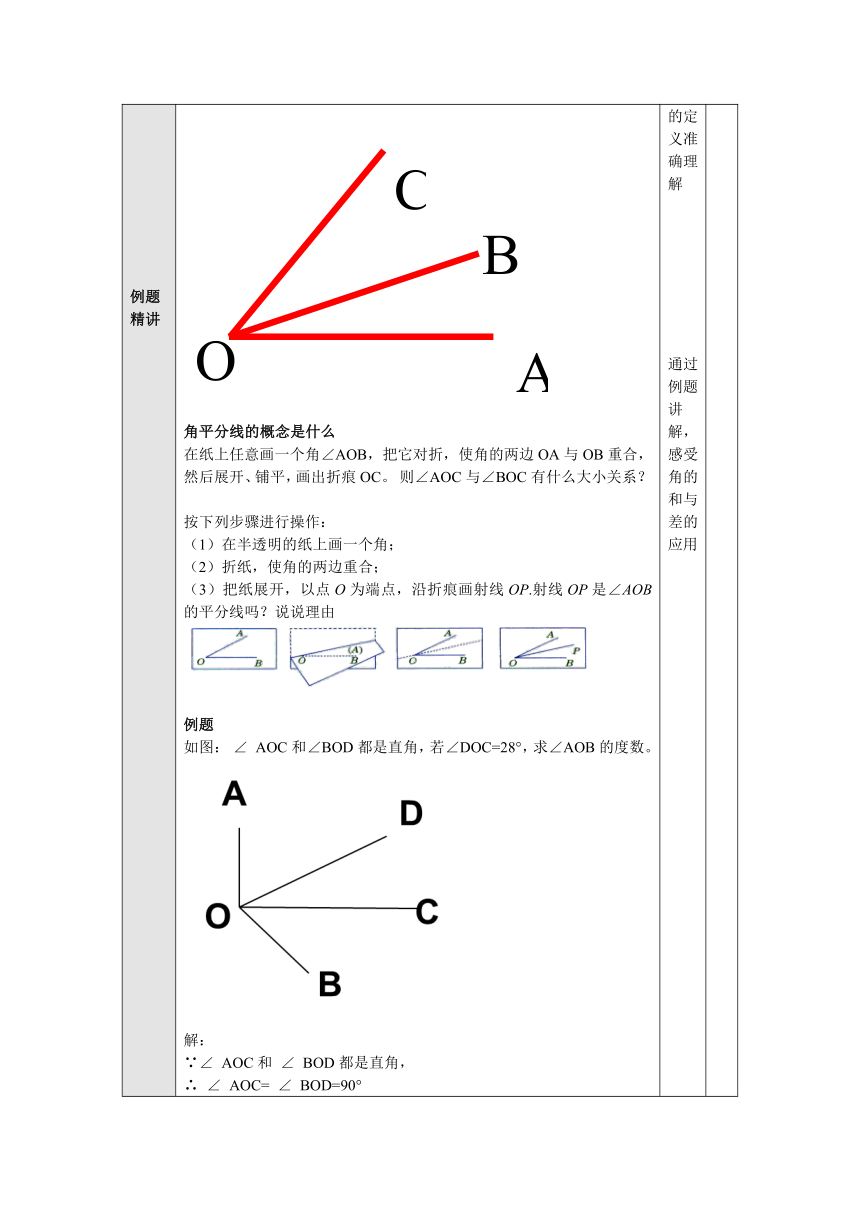
回顾旧知,引出新课 如图,用=、 < 、>填空。 (1)∠AOC ∠AOB+∠BOC (2)∠AOC ∠AOB (3)∠BOD-∠BOC ∠DOC (4)∠AOD ∠AOC+∠BOD 通过练习对旧知巩固,进入新知学习
新知探索 例题 精讲 角的和与差 思考下面的问题: 图中共有几个角? 它们之间有什么关系? 角平分线的概念是什么 在纸上任意画一个角∠AOB,把它对折,使角的两边OA与OB重合,然后展开、铺平,画出折痕OC。 则∠AOC与∠BOC有什么大小关系? 按下列步骤进行操作: (1)在半透明的纸上画一个角; (2)折纸,使角的两边重合; (3)把纸展开,以点O为端点,沿折痕画射线OP.射线OP是∠AOB的平分线吗?说说理由 例题 如图: ∠ AOC和∠BOD都是直角,若∠DOC=28°,求∠AOB的度数。 解: ∵∠ AOC和 ∠ BOD都是直角, ∴ ∠ AOC= ∠ BOD=90° ∴ ∠ AOD= ∠ AOC- ∠ DOC= 90°- 28°=62 ° ∴ ∠ AOB= ∠ BOD+ ∠ AOD= 90°+ 62 °=152 ° 了解角的和与差,特别对角平分的定义准确理解 通过例题讲解,感受角的和与差的应用
课堂检测 1、图中∠AOC= ∠BOD, 试判∠AOD和∠COB的大小, 并说明理由. 2、如图, ∠AOB =150°,OC是∠AOB的任意一条射线,OD平分∠AOC,OE平分∠BOC。问∠DOE的度数,并说明理由。 3、如图,∠AOD= 70° ,∠COD= 20 ° ,OB平分∠AOC, 那么∠AOC=___, ∠AOB= ____,∠BOD= ____ 通过练习对角的运算进一步巩固
总结提升 谈谈你对本节课学习的体会
板书设计 2.7角的和与差(1) (1)角的和与差 (2)角的平分线的定义
本课作业 同步练习
本课教育评注(实际教学效果及改进设想)
年级 七 学科 数学 主题 2.7.1角的和与差 主备教师
课型 新授课 课时 1 时间 40分钟 导学教师
教学目标 (1)结合具体图形,了解两个角的和与差的意义.会进行角的和差运算,知道如何进位或借位. (2)了解角平分线的意义及其简单应用,了角两角互余、两角互补的意义,会正确表示一个角的余角或补角,能熟练的求出一个角的余角或补角.通过探究,了解“同角(等角)的余角相等“同角(等角)的补角相等”.
教学 重、难点 重点:1、角的和与差、角平分线及其意义. 2、互余、互补的概念及其性质. 难点:两角互余、两角互补的本质特征,互余、互补的性质.
导学方法 自主学习,合作交流
导学步骤 导学行为(师生活动) 设计意图 导学教师复备
回顾旧知,引出新课 如图,用=、 < 、>填空。 (1)∠AOC ∠AOB+∠BOC (2)∠AOC ∠AOB (3)∠BOD-∠BOC ∠DOC (4)∠AOD ∠AOC+∠BOD 通过练习对旧知巩固,进入新知学习
新知探索 例题 精讲 角的和与差 思考下面的问题: 图中共有几个角? 它们之间有什么关系? 角平分线的概念是什么 在纸上任意画一个角∠AOB,把它对折,使角的两边OA与OB重合,然后展开、铺平,画出折痕OC。 则∠AOC与∠BOC有什么大小关系? 按下列步骤进行操作: (1)在半透明的纸上画一个角; (2)折纸,使角的两边重合; (3)把纸展开,以点O为端点,沿折痕画射线OP.射线OP是∠AOB的平分线吗?说说理由 例题 如图: ∠ AOC和∠BOD都是直角,若∠DOC=28°,求∠AOB的度数。 解: ∵∠ AOC和 ∠ BOD都是直角, ∴ ∠ AOC= ∠ BOD=90° ∴ ∠ AOD= ∠ AOC- ∠ DOC= 90°- 28°=62 ° ∴ ∠ AOB= ∠ BOD+ ∠ AOD= 90°+ 62 °=152 ° 了解角的和与差,特别对角平分的定义准确理解 通过例题讲解,感受角的和与差的应用
课堂检测 1、图中∠AOC= ∠BOD, 试判∠AOD和∠COB的大小, 并说明理由. 2、如图, ∠AOB =150°,OC是∠AOB的任意一条射线,OD平分∠AOC,OE平分∠BOC。问∠DOE的度数,并说明理由。 3、如图,∠AOD= 70° ,∠COD= 20 ° ,OB平分∠AOC, 那么∠AOC=___, ∠AOB= ____,∠BOD= ____ 通过练习对角的运算进一步巩固
总结提升 谈谈你对本节课学习的体会
板书设计 2.7角的和与差(1) (1)角的和与差 (2)角的平分线的定义
本课作业 同步练习
本课教育评注(实际教学效果及改进设想)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
