青岛版2021~200学年度八年级数学第一学期期中模拟检测卷(含答案)
文档属性
| 名称 | 青岛版2021~200学年度八年级数学第一学期期中模拟检测卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 746.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学第一学期期中模拟检测卷2021年11月
姓名 题号 一 二 三 四 总分
得分
一.单项选择题(共8小题,满分24分,每小题3分)
1.(3分)下列图案分别是重庆工商大学、重庆交通大学、重庆理工大学、西南大学的校徽局部图,其中是轴对称图形的是( )
A. B. C. D.
2.(3分)若点A(a,3)与B(2,b)关于x轴对称,则点M(a,b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(3分)根据分式的基本性质,分式可变形为( )
A. B. C. D.
4.(3分)分式的值为0,则x的值为( )
A.﹣2 B.2 C.﹣2或2 D.不存在这样的x
5.(3分)把代数式中的x、y同时扩大为原来的五倍后,代数式的值( )
A.扩大为原来的3倍 B.不变
C.缩小为原来的 D.扩大为原来的5倍
6.(3分)若关于x的分式方程1有一个正整数解,则整数a的值为( )
A.﹣1 B.0 C.1 D.1或﹣1
7.(3分)如图,已知△ABC的面积为16,BP平分∠ABC,且AD⊥BP于点P,则△BPC的面积是( )
A.4 B.6 C.8 D.12
8.(3分)在平面直角坐标系中,O为原点,已知点A,B的坐标分别是(2,0),(4,2),若在x轴下方有一点P,使以O,A,P为顶点的三角形与△OAB全等,则满足条件的P点的坐标是( )
A.(4,﹣2) B.(﹣4,﹣2)
C.(4,﹣2)或(﹣2,﹣2) D.(4,﹣2)或(﹣4,﹣2)
二.多项选择题(共4小题,满分12分,每小题3分)
9.(3分)下列说法错误的是( )
A.周长相等的两个三角形全等
B.如果三角形的三个内角满足∠A:∠B:∠C=1:2:3.则这个三角形是直角三角形
C.从直线外一点到这条直线的垂线段,叫做这个点到直线的距离
D.两条直线被第三条直线所截,同位角相等
10.(3分)如图,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹,
判断以下结论错误的是( )
A.∠BDE=∠BAC B.∠B=∠CAD C.AD=BD D.AE=AC
11.(3分)如图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.
方程中的x和y表示的意义,下列说法错误的是( )
A.x表示甲队每天修路的长度 B.x表示乙队每天修路的长度
C.y表示甲队修400米所用的时间 D.y表示甲队修600米所用的时间
12.(3分)如图,在△AOB和△COD中,OA=OB,OC=OD(OA<OC),∠AOB=∠COD=α,直线AC,BD交于点M,连接OM.下列结论中正确的结论是( )
A.AC=BD B.∠OAM=∠OBM
C.∠AMB=α D.OM平分∠BOC
二.填空题(共5小题,满分20分,每小题4分)
13.(4分)已知:a2﹣7a+1=0,则a2 .
14.(4分)已知关于x的分式方程无解,则m的值为 .
15.(4分)某公司需在一个月(31天)内完成新建办公楼的装修工程.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.又已知请甲工程队施工,公司每日需付费用2000元;如果请乙队施工,公司每日需付费用1400元.规定时间内:A.请甲队单独完成此项工程;B.请乙队单独完成此项工程;C.请甲、乙两队合作完成此项工程.以上三种方案中花钱最少的方案为 ;需付最少费用 元.
16.(4分)如图,∠MON=40°,点P是∠MON中的一个定点,点A、B分别在射线OM、ON移动,当△PAB的周长最小时,则∠APB的度数为 °.
17.(4分)若正整数x<y<z,且k为整数,,则(x+y)y= .
三.解答题(共7小题,满分64分)
18.(8分)解分式方程:
(1)1; (2)2.
19.(6分)先化简,再求值:(a)÷(a﹣2),其中a满足 | a |=1.
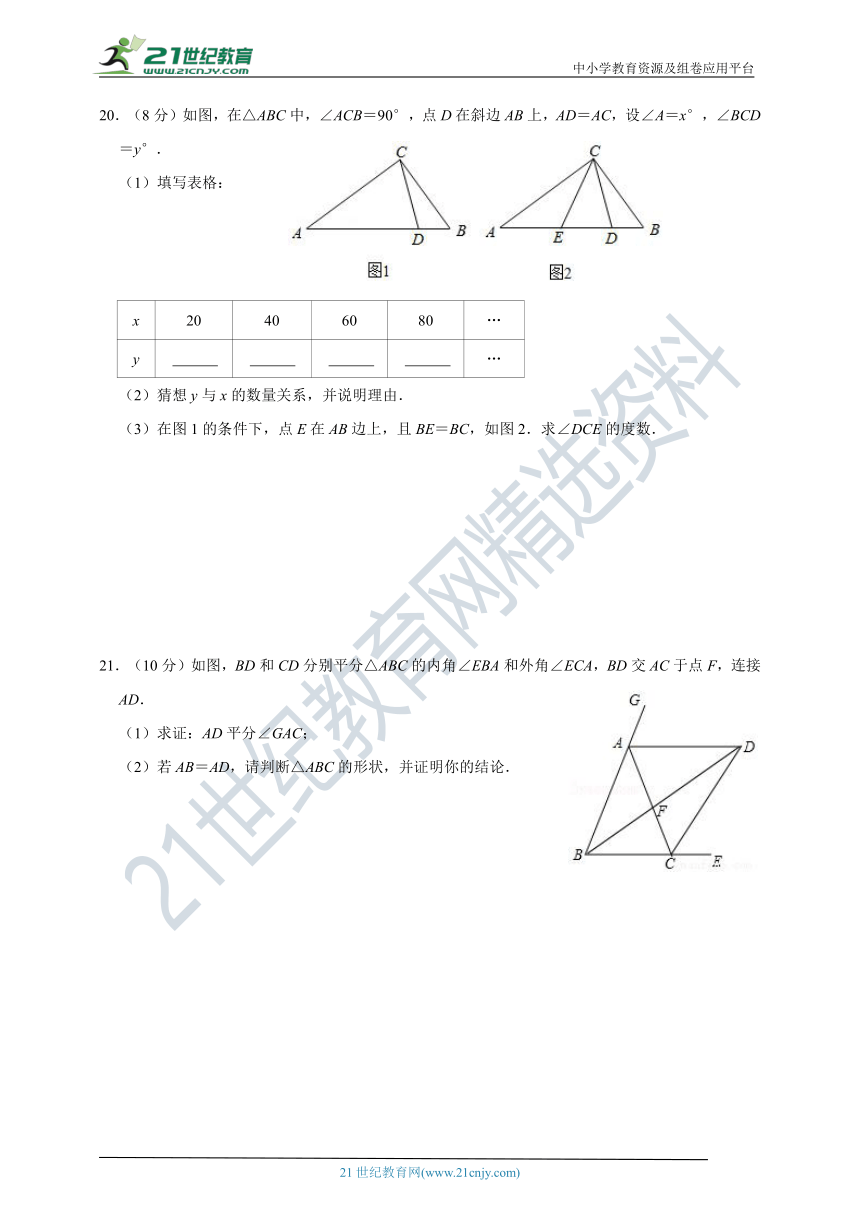
20.(8分)如图,在△ABC中,∠ACB=90°,点D在斜边AB上,AD=AC,设∠A=x°,∠BCD=y°.
(1)填写表格:
x 20 40 60 80 …
y …
(2)猜想y与x的数量关系,并说明理由.
(3)在图1的条件下,点E在AB边上,且BE=BC,如图2.求∠DCE的度数.
21.(10分)如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
22.(8分)阅读下面的解题过程:
已知x+x﹣1=3,求x3+x﹣3的值.
解:∵(x+x﹣1)2=x2+x﹣2+2=9,∴x2+x﹣2=7,
∴x3+x﹣3=(x2+x﹣2)(x+x﹣1)﹣(x+x﹣1)=7×3﹣3=18.
根据上述解题过程,解答下题:已知x+x﹣1=3,求x5+x﹣5的值.
23.(12分)某手机专卖店的一张进货单上有如下信息:A款手机进货单价比B款手机多800元,花38400元购进A款手机的数量与花28800元购进B款手机的数量相同.
(1)求A,B两款手机的进货单价分别是多少元?
(2)某周末两天销售单上的数据,如表所示:
日期 A款手机(部) B款手机(部) 销售总额(元)
星期六 5 8 40100
星期日 6 7 41100
求A,B两款手机的销售单价分别是多少元?
(3)根据(1)(2)所给的信息,手机专卖店要花费28000元购进A,B两款手机若干部,问有哪几种进货方案?根据计算说明哪种进货方案获得的总利润最高.
24.(12分)如图,∠ABC=∠BCD=90°,AB=BD,BD平分∠ABC,AE⊥BD于E,P为线段AD上一动点.
(1)求∠DAE;
(2)当P到BD的距离为1,到AB的距离为2时,求AE的长;
(3)当P运动至CE延长线上时,连接BP,求证:BP⊥AD.
八年级数学第一学期期中模拟检测卷2021年11月
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.B.
2.D.
3.D.
4.A.
5.D.
6.B.
7.C.
8.C.
9.ACD
10.BD
11.BD
12.ABC
三.填空题(共5小题,满分20分,每小题4分)
13.(4分)已知:a2﹣7a+1=0,则a2 47 .
【解答】解:∵a2﹣7a+1=0,
∴a﹣70,
则a7,
∴(a)2=49,
∴a2+249,
则a247,
14.(4分)已知关于x的分式方程无解,则m的值为 4或1 .
【解答】解:等式两边同时乘以x﹣3得:
2x﹣3﹣mx+9=x﹣3,
整理得(1﹣m)x=﹣9,
∵当x=3时为增根,方程无解,
∴3(1﹣m)=﹣9,
解得m=4,
当1﹣m=0时,x系数为0,方程无解,
解得m=1,
15.(4分)某公司需在一个月(31天)内完成新建办公楼的装修工程.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.又已知请甲工程队施工,公司每日需付费用2000元;如果请乙队施工,公司每日需付费用1400元.规定时间内:A.请甲队单独完成此项工程;B.请乙队单独完成此项工程;C.请甲、乙两队合作完成此项工程.以上三种方案中花钱最少的方案为 A ;需付最少费用 40000 元.
【解答】解:设乙队单独完成此项工程需用x天,则甲队单独完成此项工程需用(x﹣10)天.
依题意得:1,
解这个方程得x1=4,x2=30,
经检验,知x1=4,x2=30都是原方程的解,
∵x=4不合题意,
∴x=30,
则x﹣10=20,
即单独完成此项工程甲队需20天,乙队需30天;
请甲队单独完成此项工程的费用为:2000×20=40000(元),
请乙队单独完成此项工程的费用为:1400×30=42000(元),
请甲、乙两队合作完成此项工程的费用为:(2000+1400)×12=40800(元),
∵40000<40800<42000,
∴单独请甲队完成此项工程花钱最少,最少为40000元。
16.(4分)如图,∠MON=40°,点P是∠MON中的一个定点,点A、B分别在射线OM、ON移动,当△PAB的周长最小时,则∠APB的度数为 100 °.
【解答】解:如图,作点P关于OM的对称点P',点P关于ON的对称点P'',
连接OP',OP'',P'P'',其中P'P''交OM于A,交ON于B,
此时△PAB的周长最小值等于P'P''的长,
由轴对称性质可知:OP=OP',OP=OP'',∠AOP=∠AOP',∠BOP=∠BOP'',
∴∠P'OP''=2∠AOP=2×40°=80°,
∴∠P'=∠P''=(180°﹣80°)÷2=50°,
∴∠APB=∠P'+∠P''=100°,
17.(4分)若正整数x<y<z,且k为整数,,则(x+y)y= 125 .
【解答】解:∵x,y,z为正整数,且 x<y<z,
∴x≥1,y≥2,z≥3,
∴,
即 ,
又∵k 为整数,
∴k=1,x≠1.
若 x≥3,则 ,
即 ,
∴x只能为 2,
∴ 即 ,
若 y≥4,则 ,
即 .
∴y 只能为 3,
∴ 即 z=6,
综上,(x+y)y=(2+3)3=53=125.
四.解答题(共7小题,满分64分)
18.(8分)【解答】(1)解:1,
1,
x(x+2)﹣(x+2)(x﹣2)=6,
x2+2x﹣x2+4=6,
2x=2,
x=1,
检验:把x=1代入(x+2)(x﹣2)≠0,
∴原方程的解是x=1.
(2)2,
2,
2﹣x=﹣1﹣2(x﹣3),
2﹣x=﹣1﹣2x+6,
﹣x+2x=﹣1+6﹣2,
x=3,
检验:把x=3代入(x﹣3)=0,
x=3不是原方程的解,
∴原方程无解.
19.(6分)先化简,再求值:(a)÷(a﹣2),其中a满足a2﹣a﹣2=0.
【解答】解:(a)÷(a﹣2)
,
a2﹣a﹣2=0,
解得:a=2或﹣1,
根据分母(a+1)(a﹣1)得:a=﹣1不行,
当a=2时,原式3.
20.(8分)如图,在△ABC中,∠ACB=90°,点D在斜边AB上,AD=AC,设∠A=x°,∠BCD=y°.
(1)填写表格:
x 20 40 60 80 …
y 10 20 30 40 …
(2)猜想y与x的数量关系,并说明理由.
(3)在图1的条件下,点E在AB边上,且BE=BC,如图2.求∠DCE的度数.
【解答】解:(1)∵AC=AD,
∴∠ACD=∠ADC,
∵∠A=x°,
∴∠ACD,
∵∠ACB=90°,
∴∠BCD=y°=∠ACB﹣∠ACD=90°,
∴当x=20时,y=10,
当x=40时,y=20,
当x=60时,y=30,
当x=80时,y=40,
如下表格:
故答案为:10,20,30,40;
(2)猜想:yx,理由如下:
∵AC=AD,
∴∠ACD=∠ADC,
∵∠A=x°,
∴∠ACD,
∵∠ACB=90°,
∴∠BCD=y°=∠ACB﹣∠ACD=90°;
(3)如图2,Rt△ABC中,∠ACB=90°,∠A=x°,
∴∠B=90°﹣x°,
∵BC=BE,
∴∠BCE=∠BEC,
∴∠DCE=∠BCE﹣∠BCDy°=45°x°﹣y°.
21.(10分)如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
【解答】(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)解:△ABC是等腰三角形,
证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AD∥BC,
∴∠GAD=∠ABC,∠DAC=∠ACB,
∵AD平分∠GAC,
∴∠GAD=∠CAD,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
22.(8分)阅读下面的解题过程:
已知x+x﹣1=3,求x3+x﹣3的值.
解:∵(x+x﹣1)2=x2+x﹣2+2=9,∴x2+x﹣2=7,
∴x3+x﹣3=(x2+x﹣2)(x+x﹣1)﹣(x+x﹣1)=7×3﹣3=18.
根据上述解题过程,解答下题:已知x+x﹣1=3,求x5+x﹣5的值.
【解答】解:∵(x+x﹣1)2
=x2+x﹣2+2
=9,
∴x2+x﹣2=7.
∴x3+x﹣3
=(x2+x﹣2)(x+x﹣1)﹣(x+x﹣1)
=7×3﹣3
=18.
∴(x2+x﹣2)2=72.
∴x4+2+x﹣4=49.
∴x4+x﹣4=47.
∴(x+x﹣1)(x4+x﹣4)=3×47.
即x5+x﹣3+x3+x﹣5=141.
∴x5+x﹣5
=141﹣(x3+x﹣3)
=141﹣18
=123.
23.(12分)某手机专卖店的一张进货单上有如下信息:A款手机进货单价比B款手机多800元,花38400元购进A款手机的数量与花28800元购进B款手机的数量相同.
(1)求A,B两款手机的进货单价分别是多少元?
(2)某周末两天销售单上的数据,如表所示:
日期 A款手机(部) B款手机(部) 销售总额(元)
星期六 5 8 40100
星期日 6 7 41100
求A,B两款手机的销售单价分别是多少元?
(3)根据(1)(2)所给的信息,手机专卖店要花费28000元购进A,B两款手机若干部,问有哪几种进货方案?根据计算说明哪种进货方案获得的总利润最高.
【解答】解:(1)设B款手机的进货单价是x元,则A款手机的进货单价是(x+800)元,
根据题意得:,
解得:x=2400,
经检验,x=2400是原方程的解,
则x+800=2400+800=3200,
答:A款手机的进货单价是3200元,B款手机的进货单价是2400元;
(2)设A款手机的销售单价是a元,B款手机的销售单价是b元,
根据题意得:,
解得:,
答:A款手机的销售单价是3700元,B款手机的销售单价是2700元;
(3)设购买A款手机m部,B款手机n部,
根据题意,得3200m+2400n=28000,
化简得,4m+3n=35,
∵m、n都是正整数,
∴或或,
即有三种进货方案:
方案一:购买A款手机2部,B款款手机9部,利润是:(3700﹣3200)×2+(2700﹣2400)×9=3700(元);
方案二:购买A款手机5部,B款款手机5部,利润是:(3700﹣3200)×5+(2700﹣2400)×5=4000(元);
方案三:购买A款手机8部,B款款手机1部,利润是:(3700﹣3200)×8+(2700﹣2400)×1=4300(元);
∵3700<4000<4300,
∴选择方案三获得的总利润最高.
24.(12分)如图,∠ABC=∠BCD=90°,AB=BD,BD平分∠ABC,AE⊥BD于E,P为线段AD上一动点.
(1)求∠DAE;
(2)当P到BD的距离为1,到AB的距离为2时,求AE的长;
(3)当P运动至CE延长线上时,连接BP,求证:BP⊥AD.
【解答】(1)解:∵∠ABC=90°,BD平分∠ABC,
∴∠ABD45°,
∵AB=BD,
∴∠ADB=∠DAB(180°﹣∠ABD)(180°﹣45°)=67.5°,
∵AE⊥BD,
∴∠AED=90°,
∴∠DAE=90°﹣67.5°=22.5°;
(2)解:如图2,连接PB,
∵PG⊥BD,PH⊥AB,AE⊥BD,
∴S△ABD=S△BDP+S△ABPBD PGAB PHBD AE,
∵BD=AB,
∴PG+PH=AE,
∵P到BD的距离为1,到AB的距离为2,
∴AE=1+2=3;
(3)证明:∵∠ABE=∠DBC=45°,∠AEB=∠DCB=90°,
BD=AB,
∴△BDC≌△BAE(AAS),
∴BE=BC,
∴∠BEC=∠BCE=67.5°,
∴∠PED=∠PDE=67.5°,
∴PD=PE,∠AEP=22.5°,
∴∠PAE=∠AEP=22.5°,
∴AP=PE,
∴PD=AP,
∵AB=BD,
∴PB⊥AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学第一学期期中模拟检测卷2021年11月
姓名 题号 一 二 三 四 总分
得分
一.单项选择题(共8小题,满分24分,每小题3分)
1.(3分)下列图案分别是重庆工商大学、重庆交通大学、重庆理工大学、西南大学的校徽局部图,其中是轴对称图形的是( )
A. B. C. D.
2.(3分)若点A(a,3)与B(2,b)关于x轴对称,则点M(a,b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(3分)根据分式的基本性质,分式可变形为( )
A. B. C. D.
4.(3分)分式的值为0,则x的值为( )
A.﹣2 B.2 C.﹣2或2 D.不存在这样的x
5.(3分)把代数式中的x、y同时扩大为原来的五倍后,代数式的值( )
A.扩大为原来的3倍 B.不变
C.缩小为原来的 D.扩大为原来的5倍
6.(3分)若关于x的分式方程1有一个正整数解,则整数a的值为( )
A.﹣1 B.0 C.1 D.1或﹣1
7.(3分)如图,已知△ABC的面积为16,BP平分∠ABC,且AD⊥BP于点P,则△BPC的面积是( )
A.4 B.6 C.8 D.12
8.(3分)在平面直角坐标系中,O为原点,已知点A,B的坐标分别是(2,0),(4,2),若在x轴下方有一点P,使以O,A,P为顶点的三角形与△OAB全等,则满足条件的P点的坐标是( )
A.(4,﹣2) B.(﹣4,﹣2)
C.(4,﹣2)或(﹣2,﹣2) D.(4,﹣2)或(﹣4,﹣2)
二.多项选择题(共4小题,满分12分,每小题3分)
9.(3分)下列说法错误的是( )
A.周长相等的两个三角形全等
B.如果三角形的三个内角满足∠A:∠B:∠C=1:2:3.则这个三角形是直角三角形
C.从直线外一点到这条直线的垂线段,叫做这个点到直线的距离
D.两条直线被第三条直线所截,同位角相等
10.(3分)如图,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹,
判断以下结论错误的是( )
A.∠BDE=∠BAC B.∠B=∠CAD C.AD=BD D.AE=AC
11.(3分)如图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.
方程中的x和y表示的意义,下列说法错误的是( )
A.x表示甲队每天修路的长度 B.x表示乙队每天修路的长度
C.y表示甲队修400米所用的时间 D.y表示甲队修600米所用的时间
12.(3分)如图,在△AOB和△COD中,OA=OB,OC=OD(OA<OC),∠AOB=∠COD=α,直线AC,BD交于点M,连接OM.下列结论中正确的结论是( )
A.AC=BD B.∠OAM=∠OBM
C.∠AMB=α D.OM平分∠BOC
二.填空题(共5小题,满分20分,每小题4分)
13.(4分)已知:a2﹣7a+1=0,则a2 .
14.(4分)已知关于x的分式方程无解,则m的值为 .
15.(4分)某公司需在一个月(31天)内完成新建办公楼的装修工程.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.又已知请甲工程队施工,公司每日需付费用2000元;如果请乙队施工,公司每日需付费用1400元.规定时间内:A.请甲队单独完成此项工程;B.请乙队单独完成此项工程;C.请甲、乙两队合作完成此项工程.以上三种方案中花钱最少的方案为 ;需付最少费用 元.
16.(4分)如图,∠MON=40°,点P是∠MON中的一个定点,点A、B分别在射线OM、ON移动,当△PAB的周长最小时,则∠APB的度数为 °.
17.(4分)若正整数x<y<z,且k为整数,,则(x+y)y= .
三.解答题(共7小题,满分64分)
18.(8分)解分式方程:
(1)1; (2)2.
19.(6分)先化简,再求值:(a)÷(a﹣2),其中a满足 | a |=1.
20.(8分)如图,在△ABC中,∠ACB=90°,点D在斜边AB上,AD=AC,设∠A=x°,∠BCD=y°.
(1)填写表格:
x 20 40 60 80 …
y …
(2)猜想y与x的数量关系,并说明理由.
(3)在图1的条件下,点E在AB边上,且BE=BC,如图2.求∠DCE的度数.
21.(10分)如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
22.(8分)阅读下面的解题过程:
已知x+x﹣1=3,求x3+x﹣3的值.
解:∵(x+x﹣1)2=x2+x﹣2+2=9,∴x2+x﹣2=7,
∴x3+x﹣3=(x2+x﹣2)(x+x﹣1)﹣(x+x﹣1)=7×3﹣3=18.
根据上述解题过程,解答下题:已知x+x﹣1=3,求x5+x﹣5的值.
23.(12分)某手机专卖店的一张进货单上有如下信息:A款手机进货单价比B款手机多800元,花38400元购进A款手机的数量与花28800元购进B款手机的数量相同.
(1)求A,B两款手机的进货单价分别是多少元?
(2)某周末两天销售单上的数据,如表所示:
日期 A款手机(部) B款手机(部) 销售总额(元)
星期六 5 8 40100
星期日 6 7 41100
求A,B两款手机的销售单价分别是多少元?
(3)根据(1)(2)所给的信息,手机专卖店要花费28000元购进A,B两款手机若干部,问有哪几种进货方案?根据计算说明哪种进货方案获得的总利润最高.
24.(12分)如图,∠ABC=∠BCD=90°,AB=BD,BD平分∠ABC,AE⊥BD于E,P为线段AD上一动点.
(1)求∠DAE;
(2)当P到BD的距离为1,到AB的距离为2时,求AE的长;
(3)当P运动至CE延长线上时,连接BP,求证:BP⊥AD.
八年级数学第一学期期中模拟检测卷2021年11月
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.B.
2.D.
3.D.
4.A.
5.D.
6.B.
7.C.
8.C.
9.ACD
10.BD
11.BD
12.ABC
三.填空题(共5小题,满分20分,每小题4分)
13.(4分)已知:a2﹣7a+1=0,则a2 47 .
【解答】解:∵a2﹣7a+1=0,
∴a﹣70,
则a7,
∴(a)2=49,
∴a2+249,
则a247,
14.(4分)已知关于x的分式方程无解,则m的值为 4或1 .
【解答】解:等式两边同时乘以x﹣3得:
2x﹣3﹣mx+9=x﹣3,
整理得(1﹣m)x=﹣9,
∵当x=3时为增根,方程无解,
∴3(1﹣m)=﹣9,
解得m=4,
当1﹣m=0时,x系数为0,方程无解,
解得m=1,
15.(4分)某公司需在一个月(31天)内完成新建办公楼的装修工程.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.又已知请甲工程队施工,公司每日需付费用2000元;如果请乙队施工,公司每日需付费用1400元.规定时间内:A.请甲队单独完成此项工程;B.请乙队单独完成此项工程;C.请甲、乙两队合作完成此项工程.以上三种方案中花钱最少的方案为 A ;需付最少费用 40000 元.
【解答】解:设乙队单独完成此项工程需用x天,则甲队单独完成此项工程需用(x﹣10)天.
依题意得:1,
解这个方程得x1=4,x2=30,
经检验,知x1=4,x2=30都是原方程的解,
∵x=4不合题意,
∴x=30,
则x﹣10=20,
即单独完成此项工程甲队需20天,乙队需30天;
请甲队单独完成此项工程的费用为:2000×20=40000(元),
请乙队单独完成此项工程的费用为:1400×30=42000(元),
请甲、乙两队合作完成此项工程的费用为:(2000+1400)×12=40800(元),
∵40000<40800<42000,
∴单独请甲队完成此项工程花钱最少,最少为40000元。
16.(4分)如图,∠MON=40°,点P是∠MON中的一个定点,点A、B分别在射线OM、ON移动,当△PAB的周长最小时,则∠APB的度数为 100 °.
【解答】解:如图,作点P关于OM的对称点P',点P关于ON的对称点P'',
连接OP',OP'',P'P'',其中P'P''交OM于A,交ON于B,
此时△PAB的周长最小值等于P'P''的长,
由轴对称性质可知:OP=OP',OP=OP'',∠AOP=∠AOP',∠BOP=∠BOP'',
∴∠P'OP''=2∠AOP=2×40°=80°,
∴∠P'=∠P''=(180°﹣80°)÷2=50°,
∴∠APB=∠P'+∠P''=100°,
17.(4分)若正整数x<y<z,且k为整数,,则(x+y)y= 125 .
【解答】解:∵x,y,z为正整数,且 x<y<z,
∴x≥1,y≥2,z≥3,
∴,
即 ,
又∵k 为整数,
∴k=1,x≠1.
若 x≥3,则 ,
即 ,
∴x只能为 2,
∴ 即 ,
若 y≥4,则 ,
即 .
∴y 只能为 3,
∴ 即 z=6,
综上,(x+y)y=(2+3)3=53=125.
四.解答题(共7小题,满分64分)
18.(8分)【解答】(1)解:1,
1,
x(x+2)﹣(x+2)(x﹣2)=6,
x2+2x﹣x2+4=6,
2x=2,
x=1,
检验:把x=1代入(x+2)(x﹣2)≠0,
∴原方程的解是x=1.
(2)2,
2,
2﹣x=﹣1﹣2(x﹣3),
2﹣x=﹣1﹣2x+6,
﹣x+2x=﹣1+6﹣2,
x=3,
检验:把x=3代入(x﹣3)=0,
x=3不是原方程的解,
∴原方程无解.
19.(6分)先化简,再求值:(a)÷(a﹣2),其中a满足a2﹣a﹣2=0.
【解答】解:(a)÷(a﹣2)
,
a2﹣a﹣2=0,
解得:a=2或﹣1,
根据分母(a+1)(a﹣1)得:a=﹣1不行,
当a=2时,原式3.
20.(8分)如图,在△ABC中,∠ACB=90°,点D在斜边AB上,AD=AC,设∠A=x°,∠BCD=y°.
(1)填写表格:
x 20 40 60 80 …
y 10 20 30 40 …
(2)猜想y与x的数量关系,并说明理由.
(3)在图1的条件下,点E在AB边上,且BE=BC,如图2.求∠DCE的度数.
【解答】解:(1)∵AC=AD,
∴∠ACD=∠ADC,
∵∠A=x°,
∴∠ACD,
∵∠ACB=90°,
∴∠BCD=y°=∠ACB﹣∠ACD=90°,
∴当x=20时,y=10,
当x=40时,y=20,
当x=60时,y=30,
当x=80时,y=40,
如下表格:
故答案为:10,20,30,40;
(2)猜想:yx,理由如下:
∵AC=AD,
∴∠ACD=∠ADC,
∵∠A=x°,
∴∠ACD,
∵∠ACB=90°,
∴∠BCD=y°=∠ACB﹣∠ACD=90°;
(3)如图2,Rt△ABC中,∠ACB=90°,∠A=x°,
∴∠B=90°﹣x°,
∵BC=BE,
∴∠BCE=∠BEC,
∴∠DCE=∠BCE﹣∠BCDy°=45°x°﹣y°.
21.(10分)如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
【解答】(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)解:△ABC是等腰三角形,
证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AD∥BC,
∴∠GAD=∠ABC,∠DAC=∠ACB,
∵AD平分∠GAC,
∴∠GAD=∠CAD,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
22.(8分)阅读下面的解题过程:
已知x+x﹣1=3,求x3+x﹣3的值.
解:∵(x+x﹣1)2=x2+x﹣2+2=9,∴x2+x﹣2=7,
∴x3+x﹣3=(x2+x﹣2)(x+x﹣1)﹣(x+x﹣1)=7×3﹣3=18.
根据上述解题过程,解答下题:已知x+x﹣1=3,求x5+x﹣5的值.
【解答】解:∵(x+x﹣1)2
=x2+x﹣2+2
=9,
∴x2+x﹣2=7.
∴x3+x﹣3
=(x2+x﹣2)(x+x﹣1)﹣(x+x﹣1)
=7×3﹣3
=18.
∴(x2+x﹣2)2=72.
∴x4+2+x﹣4=49.
∴x4+x﹣4=47.
∴(x+x﹣1)(x4+x﹣4)=3×47.
即x5+x﹣3+x3+x﹣5=141.
∴x5+x﹣5
=141﹣(x3+x﹣3)
=141﹣18
=123.
23.(12分)某手机专卖店的一张进货单上有如下信息:A款手机进货单价比B款手机多800元,花38400元购进A款手机的数量与花28800元购进B款手机的数量相同.
(1)求A,B两款手机的进货单价分别是多少元?
(2)某周末两天销售单上的数据,如表所示:
日期 A款手机(部) B款手机(部) 销售总额(元)
星期六 5 8 40100
星期日 6 7 41100
求A,B两款手机的销售单价分别是多少元?
(3)根据(1)(2)所给的信息,手机专卖店要花费28000元购进A,B两款手机若干部,问有哪几种进货方案?根据计算说明哪种进货方案获得的总利润最高.
【解答】解:(1)设B款手机的进货单价是x元,则A款手机的进货单价是(x+800)元,
根据题意得:,
解得:x=2400,
经检验,x=2400是原方程的解,
则x+800=2400+800=3200,
答:A款手机的进货单价是3200元,B款手机的进货单价是2400元;
(2)设A款手机的销售单价是a元,B款手机的销售单价是b元,
根据题意得:,
解得:,
答:A款手机的销售单价是3700元,B款手机的销售单价是2700元;
(3)设购买A款手机m部,B款手机n部,
根据题意,得3200m+2400n=28000,
化简得,4m+3n=35,
∵m、n都是正整数,
∴或或,
即有三种进货方案:
方案一:购买A款手机2部,B款款手机9部,利润是:(3700﹣3200)×2+(2700﹣2400)×9=3700(元);
方案二:购买A款手机5部,B款款手机5部,利润是:(3700﹣3200)×5+(2700﹣2400)×5=4000(元);
方案三:购买A款手机8部,B款款手机1部,利润是:(3700﹣3200)×8+(2700﹣2400)×1=4300(元);
∵3700<4000<4300,
∴选择方案三获得的总利润最高.
24.(12分)如图,∠ABC=∠BCD=90°,AB=BD,BD平分∠ABC,AE⊥BD于E,P为线段AD上一动点.
(1)求∠DAE;
(2)当P到BD的距离为1,到AB的距离为2时,求AE的长;
(3)当P运动至CE延长线上时,连接BP,求证:BP⊥AD.
【解答】(1)解:∵∠ABC=90°,BD平分∠ABC,
∴∠ABD45°,
∵AB=BD,
∴∠ADB=∠DAB(180°﹣∠ABD)(180°﹣45°)=67.5°,
∵AE⊥BD,
∴∠AED=90°,
∴∠DAE=90°﹣67.5°=22.5°;
(2)解:如图2,连接PB,
∵PG⊥BD,PH⊥AB,AE⊥BD,
∴S△ABD=S△BDP+S△ABPBD PGAB PHBD AE,
∵BD=AB,
∴PG+PH=AE,
∵P到BD的距离为1,到AB的距离为2,
∴AE=1+2=3;
(3)证明:∵∠ABE=∠DBC=45°,∠AEB=∠DCB=90°,
BD=AB,
∴△BDC≌△BAE(AAS),
∴BE=BC,
∴∠BEC=∠BCE=67.5°,
∴∠PED=∠PDE=67.5°,
∴PD=PE,∠AEP=22.5°,
∴∠PAE=∠AEP=22.5°,
∴AP=PE,
∴PD=AP,
∵AB=BD,
∴PB⊥AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
