2020-2021学年上海市徐汇区西南位育中学八年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市徐汇区西南位育中学八年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 358.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 11:12:15 | ||
图片预览



文档简介
2020-2021学年上海市徐汇区西南位育中学八年级(上)期中数学试卷
一、选择题(每题2分,共12分).
1.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
2.(2分)下列二次根式中,不是最简二次根式的是( )
A. B.
C. D.
3.(2分)下列多项式能在实数范围内因式分解的是( )
A.x2+9 B.x2+2x+7 C.2x2﹣3x﹣6 D.4x2﹣2x+1
4.(2分)下列关于x的方程一定是一元二次方程的是( )
A.x2+2x=x2﹣1 B.m2x2﹣7+x2=0
C.x2+﹣1=0 D.ax2+bx+c=0
5.(2分)化简:(2a﹣3b)=( )
A.﹣1 B.1 C. D.﹣
6.(2分)下列命题中,真命题是( )
A.三角形的一个外角大于这个三角形的内角
B.如果两个角的两边分别平行,那么这两个角相等
C.一对邻补角的角平分线互相垂直
D.面积相等的两个三角形全等
二、填空题:(每题2分,共24分)
7.(2分)计算:×= .
8.(2分)计算:= .
9.(2分)方程x2=x的根是 .
10.(2分)如果等式成立,那么x的取值范围是 .
11.(2分)写出2的一个有理化因式可以是 .
12.(2分)在实数范围内因式分解:2x2﹣3xy﹣y2= .
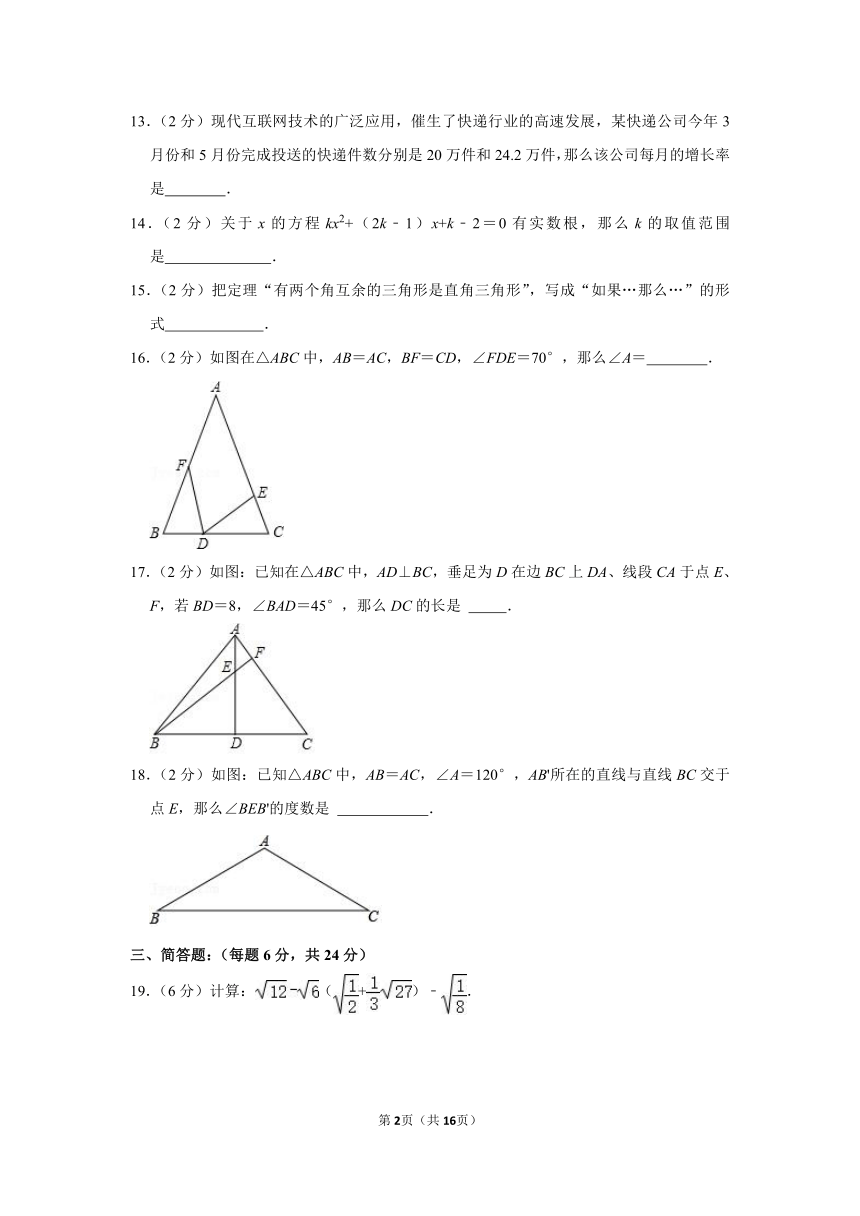
13.(2分)现代互联网技术的广泛应用,催生了快递行业的高速发展,某快递公司今年3月份和5月份完成投送的快递件数分别是20万件和24.2万件,那么该公司每月的增长率是 .
14.(2分)关于x的方程kx2+(2k﹣1)x+k﹣2=0有实数根,那么k的取值范围是 .
15.(2分)把定理“有两个角互余的三角形是直角三角形”,写成“如果…那么…”的形式 .
16.(2分)如图在△ABC中,AB=AC,BF=CD,∠FDE=70°,那么∠A= .
17.(2分)如图:已知在△ABC中,AD⊥BC,垂足为D在边BC上DA、线段CA于点E、F,若BD=8,∠BAD=45°,那么DC的长是 .
18.(2分)如图:已知△ABC中,AB=AC,∠A=120°,AB'所在的直线与直线BC交于点E,那么∠BEB'的度数是 .
三、简答题:(每题6分,共24分)
19.(6分)计算:(+)﹣.
20.(6分)解不等式:.
21.(6分)用适当的方法解方程:2x(x﹣2)=x2+5.
22.(6分)用配方法解方程:3x2+5x﹣1=0.
四、解答题:(第23、24、25、26、27每题8分,共40分)
23.(8分)已知关于x的方程(m﹣1)x2﹣(m﹣5)x=﹣有两个相等的实数根.
24.(8分)如图,AD∥BC,点E是AB的中点,点G在边BC上,且∠GDF=∠ADF.
(1)求证:AD=BF;
(2)当点G是FC的中点时,判断△FDC的形状.
25.(8分)如图,某农场有一道长16米的围墙,计划用40米长的围栏靠墙围成一个面积为120平方米的长方形养鸡场,在墙的对面开了两个1米宽的门,求围成长方形养鸡场宽AB的长度.
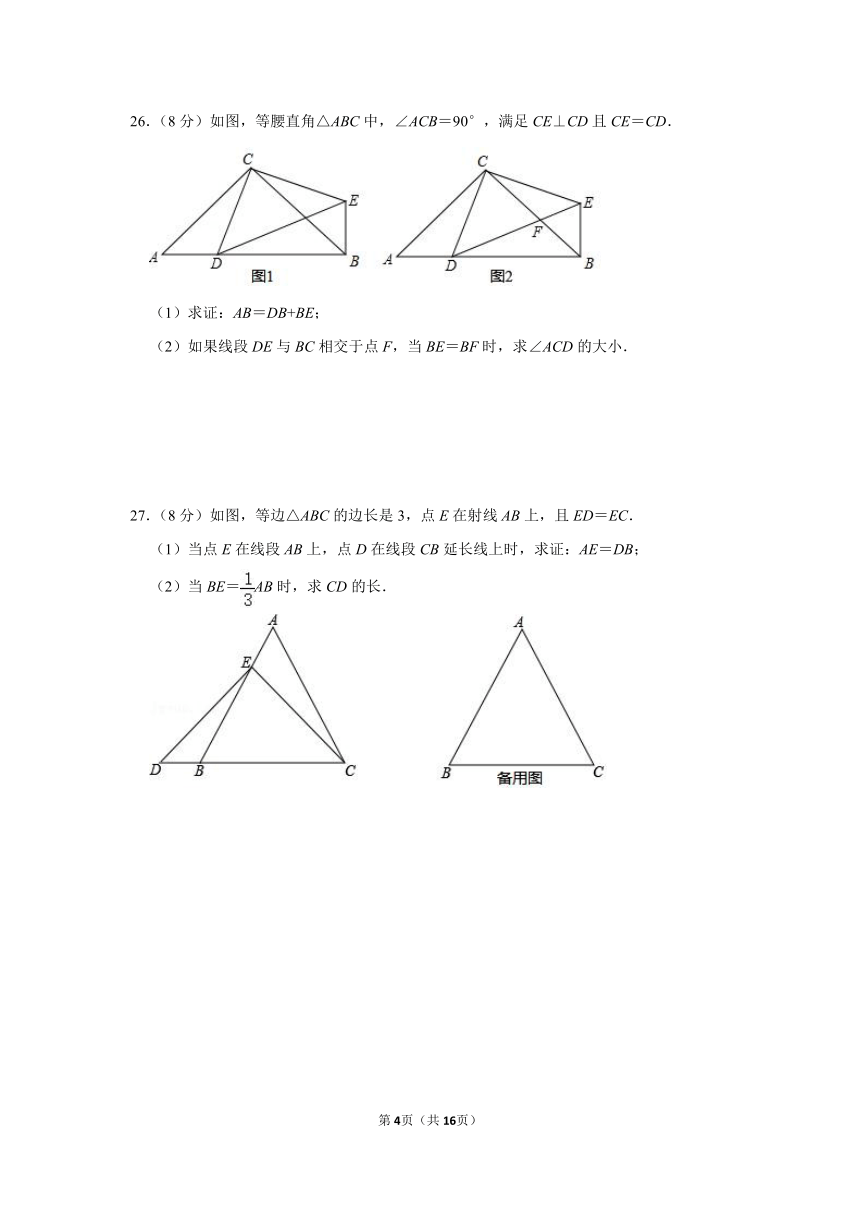
26.(8分)如图,等腰直角△ABC中,∠ACB=90°,满足CE⊥CD且CE=CD.
(1)求证:AB=DB+BE;
(2)如果线段DE与BC相交于点F,当BE=BF时,求∠ACD的大小.
27.(8分)如图,等边△ABC的边长是3,点E在射线AB上,且ED=EC.
(1)当点E在线段AB上,点D在线段CB延长线上时,求证:AE=DB;
(2)当BE=AB时,求CD的长.
2020-2021学年上海市徐汇区西南位育中学八年级(上)期中数学试卷
参考答案与试题解析
一、选择题:(每题2分,共12分)
1.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【解答】解:A、=3,与,不符合题意;
B、=,与不是同类二次根式;
C、与不是同类二次根式;
D、=,与是同类二次根式;
故选:D.
2.(2分)下列二次根式中,不是最简二次根式的是( )
A. B.
C. D.
【解答】解:A、是最简二次根式;
B、是最简二次根式;
C、是最简二次根式;
D、=|a﹣b|,故本选项符合题意;
故选:D.
3.(2分)下列多项式能在实数范围内因式分解的是( )
A.x2+9 B.x2+2x+7 C.2x2﹣3x﹣6 D.4x2﹣2x+1
【解答】解:A、令x2+9=5,Δ=b2﹣4ac=﹣36<5,即方程无解;
B、令x2+2x+5=0,Δ=b2﹣4ac=4﹣28=﹣24<0,即方程无解;
C、令2x2﹣3x﹣7=0,Δ=b2﹣3ac=9+48=57>0,即方程有两个不相等的实数根;
D、令2x2﹣2x+7=0,Δ=b2﹣4ac=4﹣16=﹣12<0,即方程无解.
故选:C.
4.(2分)下列关于x的方程一定是一元二次方程的是( )
A.x2+2x=x2﹣1 B.m2x2﹣7+x2=0
C.x2+﹣1=0 D.ax2+bx+c=0
【解答】解:A、x2+2x=x6﹣1,整理后是一元一次方程;
B、m2x6﹣7+x2=4是一元二次方程,故此选项符合题意;
C、x2+﹣5=0不是整式方程,故此选项不符合题意;
D、ax2+bx+c=8,a=0时,故此选项不符合题意.
故选:B.
5.(2分)化简:(2a﹣3b)=( )
A.﹣1 B.1 C. D.﹣
【解答】解:由题意得,3b﹣2a>8,
∴原式=﹣=﹣,
故选:D.
6.(2分)下列命题中,真命题是( )
A.三角形的一个外角大于这个三角形的内角
B.如果两个角的两边分别平行,那么这两个角相等
C.一对邻补角的角平分线互相垂直
D.面积相等的两个三角形全等
【解答】解:A、三角形的一个外角大于这个三角形与它不相邻的内角,不符合题意;
B、如果两个角的两边分别平行,本选项说法是假命题;
C、一对邻补角的角平分线互相垂直,符合题意;
D、面积相等的两个三角形不一定全等,不符合题意;
故选:C.
二、填空题:(每题2分,共24分)
7.(2分)计算:×= 6 .
【解答】解:原式=2×=6.
故答案为:6.
8.(2分)计算:= 3﹣ .
【解答】解:=3﹣.
故答案为:3﹣.
9.(2分)方程x2=x的根是 x1=0,x2=1 .
【解答】解:x2﹣x=0,
x(x﹣6)=0,
∴x=0或x﹣3=0,
∴x1=7,x2=1.
故答案为x4=0,x2=8.
10.(2分)如果等式成立,那么x的取值范围是 x≤1 .
【解答】解:∵等式成立,
∴4﹣x≥4且1﹣x≥0,
∴x≤7且x≤1,
∴x≤1,
故答案为:x≤8.
11.(2分)写出2的一个有理化因式可以是 (答案不唯一) .
【解答】解:2的一个有理化因式可以是.
故答案为:(答案不唯一).
12.(2分)在实数范围内因式分解:2x2﹣3xy﹣y2= 2(x﹣y)(x﹣y) .
【解答】解:2x2﹣4xy﹣y2=0的解是x8=y,x5=y,
∴3x2﹣3xy﹣y6=2(x﹣y)(x﹣,
故答案为:4(x﹣y)(x﹣.
13.(2分)现代互联网技术的广泛应用,催生了快递行业的高速发展,某快递公司今年3月份和5月份完成投送的快递件数分别是20万件和24.2万件,那么该公司每月的增长率是 10% .
【解答】解:设该快递公司投递快递总件数的月平均增长率为x,由题意,得
20×(1+x)2=24.4,
解得:x1=10%,x2=﹣210%(不合题意舍去).
答:该快递公司投递快递总件数的月平均增长率为10%.
故答案是:10%.
14.(2分)关于x的方程kx2+(2k﹣1)x+k﹣2=0有实数根,那么k的取值范围是 k≥﹣ .
【解答】解:∵关于x的方程kx2+(2k﹣3)x+k﹣2=0有实数根,
当 k≠5时,
∴Δ=b2﹣4ac≥7,
即:(2k﹣1)3﹣4k(k﹣2)≥2,
解得:k≥﹣,
当k=3时,x=﹣2,
故答案为:k≥﹣.
15.(2分)把定理“有两个角互余的三角形是直角三角形”,写成“如果…那么…”的形式: 如果一个三角形有两个角互余,那么这个三角形是直角三角形 .
【解答】解:定理“有两个角互余的三角形是直角三角形”,写成“如果…那么…”的形式:如果一个三角形有两个角互余,
故答案为:如果一个三角形有两个角互余,那么这个三角形是直角三角形.
16.(2分)如图在△ABC中,AB=AC,BF=CD,∠FDE=70°,那么∠A= 40° .
【解答】解:∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∴∠FDE=180°﹣∠CDE﹣∠BDF=180°﹣∠BFD﹣∠BDF=∠B,
∵∠FDE=70°,
∴∠B=70°,
∵∠B+∠C+∠A=180°,
∴∠A=40°.
故答案为:40°.
17.(2分)如图:已知在△ABC中,AD⊥BC,垂足为D在边BC上
DA、线段CA于点E、F,若BD=8,∠BAD=45°,那么DC的长是 6 .
【解答】解:∵AD⊥BC,∠BAD=45°,
∴∠ABD=∠BAD=45°,
∴BD=AD,
∵AD⊥BC,
∴∠C+∠DAC=90°,
同理:∠C+∠EBD=90°,
∴∠EBD=∠DAC,
在△BDE和△ADC中,
,
∴△BDE≌△ADC(ASA),
∴BD=AD=8,DE=DC,
∵DE=AD﹣AE=8﹣6=6,
∴DC=DE=6.
故答案为:4.
18.(2分)如图:已知△ABC中,AB=AC,∠A=120°,AB'所在的直线与直线BC交于点E,那么∠BEB'的度数是 10°或50° .
【解答】解:如图1,将△ABC绕点A顺时针旋转20°得到△AB'C',
∵AB=AC,∠BAC=120°,
∴∠ABC=30°,
∵∠BAE=20°,
∴∠BEB'=∠ABC﹣∠BAE=30°﹣20°=10°;
如图2,将△ABC绕点A逆时针旋转20°得到△AB'C',
∵AB=AC,∠BAC=120°,
∴∠ABC=30°,
∵∠BAE=20°,
∴∠BEB'=∠ABC+∠BAE=30°+20°=50°;
综合以上可得∠BEB'的度数是10°或50°.
故答案为10°或50°.
三、简答题:(每题6分,共24分)
19.(6分)计算:(+)﹣.
【解答】解:原式=2﹣×(
=2﹣﹣3﹣
=﹣3﹣.
20.(6分)解不等式:.
【解答】解:,
x﹣7≤3x﹣,
则x﹣3x≤,
(﹣3)x≤,
解得:x≥,
x≥﹣4﹣4.
21.(6分)用适当的方法解方程:2x(x﹣2)=x2+5.
【解答】解:整理得:2x2﹣2x﹣5=0,
(x﹣6)(x+1)=0,
∴x﹣5=0或x+1=5,
∴x1=5,x2=﹣1.
22.(6分)用配方法解方程:3x2+5x﹣1=0.
【解答】解:3x2+5x﹣1=0,
3x2+5x=3,
x2+x=,
x5+x+()2=+()2,
(x+)2=,
∴x+=±,
∴x1=,x2=.
四、解答题:(第23、24、25、26、27每题8分,共40分)
23.(8分)已知关于x的方程(m﹣1)x2﹣(m﹣5)x=﹣有两个相等的实数根
【解答】解:原方程可化为(m﹣1)x2﹣(m﹣8)x+=2,
根据题意得Δ=[﹣(m﹣5)]2﹣8(m﹣1)×=0,
解得m=3或4.
当m=3时,此时方程为2x2+2x+=0)2=0,
解得x5=x2=﹣;
当m=9时,此时方程为8x7﹣4x+=0)2=0,
解得x7=x2=.
24.(8分)如图,AD∥BC,点E是AB的中点,点G在边BC上,且∠GDF=∠ADF.
(1)求证:AD=BF;
(2)当点G是FC的中点时,判断△FDC的形状.
【解答】(1)证明:∵AD∥BC,
∴∠ADE=∠BFE,
∵E为AB的中点,
∴AE=BE,
在△ADE和△BFE中,
,
∴△ADE≌△BFE(AAS),
∴AD=BF;
(2)解:△FDC是直角三角形,理由如下:
连接EG,
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△ADE≌△BFE得:DE=FE,
即GE为DF上的中线,
∴GE⊥DF,
∵点G是FC的中点,DE=FE,
∴GE∥CD,
∴CD⊥DF,
∴△FDC是直角三角形.
25.(8分)如图,某农场有一道长16米的围墙,计划用40米长的围栏靠墙围成一个面积为120平方米的长方形养鸡场,在墙的对面开了两个1米宽的门,求围成长方形养鸡场宽AB的长度.
【解答】解:设长方形养鸡场AB边的长度为x米,则BC边的长度为(42﹣3x)米,
依题意,得:x(42﹣3x)=120,
整理,得:x6=4,x2=10.
∵42﹣7x≤16,
∴x≥,
∴x=4.
答:围成长方形养鸡场AB边的长度为10米.
26.(8分)如图,等腰直角△ABC中,∠ACB=90°,满足CE⊥CD且CE=CD.
(1)求证:AB=DB+BE;
(2)如果线段DE与BC相交于点F,当BE=BF时,求∠ACD的大小.
【解答】(1)证明:∵CE⊥CD,
∴∠DCE=90°=∠ACB,
∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,
即∠ACD=∠BCE,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,∠A=∠CBA=45°,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴AB=DB+AD=DB+BE;
(2)解:由(1)知,∠ACD=∠BCE,
∴∠CAD=∠CBE=45°,
∵CE⊥CD且CE=CD,
∴△CDE是等腰直角三角形,
∴∠CED=45°,
∵BF=BE,
∴∠BFE=∠BEF=(180°﹣45°)=67.7°,
∵∠BFE=∠BCE+∠CEF,
∴∠BCE=67.5°﹣45°=22.5°,
∴∠ACD=22.2°.
27.(8分)如图,等边△ABC的边长是3,点E在射线AB上,且ED=EC.
(1)当点E在线段AB上,点D在线段CB延长线上时,求证:AE=DB;
(2)当BE=AB时,求CD的长.
【解答】(1)证明:过E作EF∥BC交AC于F,如图所示:
∵ED=EC,
∴∠D=∠ECD,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,
∴∠DBE=120°,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠A=∠AEF=∠AFE=60°,
∴△AEF是等边三角形,∠EFC=120°,
∴EF=AE,
∵EF∥BC,
∴∠FEC=∠ECD,
∴∠D=∠FEC,
在△EFC和△DBE中,
,
∴△EFC≌△DBE(AAS),
∴EF=DB,
∴AE=DB;
(2)解:过E作EF∥BC交AC于F,如图所示:
∵等边△ABC的边长是3,
∴AB=BC=3,
∵BE=AB=1,
∴AE=AB﹣BE=2,
由(1)知,△EFC≌△DBE,
∴DB=AE=2,
∵CD=DB+BC=2+6=5.
第1页(共1页)
一、选择题(每题2分,共12分).
1.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
2.(2分)下列二次根式中,不是最简二次根式的是( )
A. B.
C. D.
3.(2分)下列多项式能在实数范围内因式分解的是( )
A.x2+9 B.x2+2x+7 C.2x2﹣3x﹣6 D.4x2﹣2x+1
4.(2分)下列关于x的方程一定是一元二次方程的是( )
A.x2+2x=x2﹣1 B.m2x2﹣7+x2=0
C.x2+﹣1=0 D.ax2+bx+c=0
5.(2分)化简:(2a﹣3b)=( )
A.﹣1 B.1 C. D.﹣
6.(2分)下列命题中,真命题是( )
A.三角形的一个外角大于这个三角形的内角
B.如果两个角的两边分别平行,那么这两个角相等
C.一对邻补角的角平分线互相垂直
D.面积相等的两个三角形全等
二、填空题:(每题2分,共24分)
7.(2分)计算:×= .
8.(2分)计算:= .
9.(2分)方程x2=x的根是 .
10.(2分)如果等式成立,那么x的取值范围是 .
11.(2分)写出2的一个有理化因式可以是 .
12.(2分)在实数范围内因式分解:2x2﹣3xy﹣y2= .
13.(2分)现代互联网技术的广泛应用,催生了快递行业的高速发展,某快递公司今年3月份和5月份完成投送的快递件数分别是20万件和24.2万件,那么该公司每月的增长率是 .
14.(2分)关于x的方程kx2+(2k﹣1)x+k﹣2=0有实数根,那么k的取值范围是 .
15.(2分)把定理“有两个角互余的三角形是直角三角形”,写成“如果…那么…”的形式 .
16.(2分)如图在△ABC中,AB=AC,BF=CD,∠FDE=70°,那么∠A= .
17.(2分)如图:已知在△ABC中,AD⊥BC,垂足为D在边BC上DA、线段CA于点E、F,若BD=8,∠BAD=45°,那么DC的长是 .
18.(2分)如图:已知△ABC中,AB=AC,∠A=120°,AB'所在的直线与直线BC交于点E,那么∠BEB'的度数是 .
三、简答题:(每题6分,共24分)
19.(6分)计算:(+)﹣.
20.(6分)解不等式:.
21.(6分)用适当的方法解方程:2x(x﹣2)=x2+5.
22.(6分)用配方法解方程:3x2+5x﹣1=0.
四、解答题:(第23、24、25、26、27每题8分,共40分)
23.(8分)已知关于x的方程(m﹣1)x2﹣(m﹣5)x=﹣有两个相等的实数根.
24.(8分)如图,AD∥BC,点E是AB的中点,点G在边BC上,且∠GDF=∠ADF.
(1)求证:AD=BF;
(2)当点G是FC的中点时,判断△FDC的形状.
25.(8分)如图,某农场有一道长16米的围墙,计划用40米长的围栏靠墙围成一个面积为120平方米的长方形养鸡场,在墙的对面开了两个1米宽的门,求围成长方形养鸡场宽AB的长度.
26.(8分)如图,等腰直角△ABC中,∠ACB=90°,满足CE⊥CD且CE=CD.
(1)求证:AB=DB+BE;
(2)如果线段DE与BC相交于点F,当BE=BF时,求∠ACD的大小.
27.(8分)如图,等边△ABC的边长是3,点E在射线AB上,且ED=EC.
(1)当点E在线段AB上,点D在线段CB延长线上时,求证:AE=DB;
(2)当BE=AB时,求CD的长.
2020-2021学年上海市徐汇区西南位育中学八年级(上)期中数学试卷
参考答案与试题解析
一、选择题:(每题2分,共12分)
1.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【解答】解:A、=3,与,不符合题意;
B、=,与不是同类二次根式;
C、与不是同类二次根式;
D、=,与是同类二次根式;
故选:D.
2.(2分)下列二次根式中,不是最简二次根式的是( )
A. B.
C. D.
【解答】解:A、是最简二次根式;
B、是最简二次根式;
C、是最简二次根式;
D、=|a﹣b|,故本选项符合题意;
故选:D.
3.(2分)下列多项式能在实数范围内因式分解的是( )
A.x2+9 B.x2+2x+7 C.2x2﹣3x﹣6 D.4x2﹣2x+1
【解答】解:A、令x2+9=5,Δ=b2﹣4ac=﹣36<5,即方程无解;
B、令x2+2x+5=0,Δ=b2﹣4ac=4﹣28=﹣24<0,即方程无解;
C、令2x2﹣3x﹣7=0,Δ=b2﹣3ac=9+48=57>0,即方程有两个不相等的实数根;
D、令2x2﹣2x+7=0,Δ=b2﹣4ac=4﹣16=﹣12<0,即方程无解.
故选:C.
4.(2分)下列关于x的方程一定是一元二次方程的是( )
A.x2+2x=x2﹣1 B.m2x2﹣7+x2=0
C.x2+﹣1=0 D.ax2+bx+c=0
【解答】解:A、x2+2x=x6﹣1,整理后是一元一次方程;
B、m2x6﹣7+x2=4是一元二次方程,故此选项符合题意;
C、x2+﹣5=0不是整式方程,故此选项不符合题意;
D、ax2+bx+c=8,a=0时,故此选项不符合题意.
故选:B.
5.(2分)化简:(2a﹣3b)=( )
A.﹣1 B.1 C. D.﹣
【解答】解:由题意得,3b﹣2a>8,
∴原式=﹣=﹣,
故选:D.
6.(2分)下列命题中,真命题是( )
A.三角形的一个外角大于这个三角形的内角
B.如果两个角的两边分别平行,那么这两个角相等
C.一对邻补角的角平分线互相垂直
D.面积相等的两个三角形全等
【解答】解:A、三角形的一个外角大于这个三角形与它不相邻的内角,不符合题意;
B、如果两个角的两边分别平行,本选项说法是假命题;
C、一对邻补角的角平分线互相垂直,符合题意;
D、面积相等的两个三角形不一定全等,不符合题意;
故选:C.
二、填空题:(每题2分,共24分)
7.(2分)计算:×= 6 .
【解答】解:原式=2×=6.
故答案为:6.
8.(2分)计算:= 3﹣ .
【解答】解:=3﹣.
故答案为:3﹣.
9.(2分)方程x2=x的根是 x1=0,x2=1 .
【解答】解:x2﹣x=0,
x(x﹣6)=0,
∴x=0或x﹣3=0,
∴x1=7,x2=1.
故答案为x4=0,x2=8.
10.(2分)如果等式成立,那么x的取值范围是 x≤1 .
【解答】解:∵等式成立,
∴4﹣x≥4且1﹣x≥0,
∴x≤7且x≤1,
∴x≤1,
故答案为:x≤8.
11.(2分)写出2的一个有理化因式可以是 (答案不唯一) .
【解答】解:2的一个有理化因式可以是.
故答案为:(答案不唯一).
12.(2分)在实数范围内因式分解:2x2﹣3xy﹣y2= 2(x﹣y)(x﹣y) .
【解答】解:2x2﹣4xy﹣y2=0的解是x8=y,x5=y,
∴3x2﹣3xy﹣y6=2(x﹣y)(x﹣,
故答案为:4(x﹣y)(x﹣.
13.(2分)现代互联网技术的广泛应用,催生了快递行业的高速发展,某快递公司今年3月份和5月份完成投送的快递件数分别是20万件和24.2万件,那么该公司每月的增长率是 10% .
【解答】解:设该快递公司投递快递总件数的月平均增长率为x,由题意,得
20×(1+x)2=24.4,
解得:x1=10%,x2=﹣210%(不合题意舍去).
答:该快递公司投递快递总件数的月平均增长率为10%.
故答案是:10%.
14.(2分)关于x的方程kx2+(2k﹣1)x+k﹣2=0有实数根,那么k的取值范围是 k≥﹣ .
【解答】解:∵关于x的方程kx2+(2k﹣3)x+k﹣2=0有实数根,
当 k≠5时,
∴Δ=b2﹣4ac≥7,
即:(2k﹣1)3﹣4k(k﹣2)≥2,
解得:k≥﹣,
当k=3时,x=﹣2,
故答案为:k≥﹣.
15.(2分)把定理“有两个角互余的三角形是直角三角形”,写成“如果…那么…”的形式: 如果一个三角形有两个角互余,那么这个三角形是直角三角形 .
【解答】解:定理“有两个角互余的三角形是直角三角形”,写成“如果…那么…”的形式:如果一个三角形有两个角互余,
故答案为:如果一个三角形有两个角互余,那么这个三角形是直角三角形.
16.(2分)如图在△ABC中,AB=AC,BF=CD,∠FDE=70°,那么∠A= 40° .
【解答】解:∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∴∠FDE=180°﹣∠CDE﹣∠BDF=180°﹣∠BFD﹣∠BDF=∠B,
∵∠FDE=70°,
∴∠B=70°,
∵∠B+∠C+∠A=180°,
∴∠A=40°.
故答案为:40°.
17.(2分)如图:已知在△ABC中,AD⊥BC,垂足为D在边BC上
DA、线段CA于点E、F,若BD=8,∠BAD=45°,那么DC的长是 6 .
【解答】解:∵AD⊥BC,∠BAD=45°,
∴∠ABD=∠BAD=45°,
∴BD=AD,
∵AD⊥BC,
∴∠C+∠DAC=90°,
同理:∠C+∠EBD=90°,
∴∠EBD=∠DAC,
在△BDE和△ADC中,
,
∴△BDE≌△ADC(ASA),
∴BD=AD=8,DE=DC,
∵DE=AD﹣AE=8﹣6=6,
∴DC=DE=6.
故答案为:4.
18.(2分)如图:已知△ABC中,AB=AC,∠A=120°,AB'所在的直线与直线BC交于点E,那么∠BEB'的度数是 10°或50° .
【解答】解:如图1,将△ABC绕点A顺时针旋转20°得到△AB'C',
∵AB=AC,∠BAC=120°,
∴∠ABC=30°,
∵∠BAE=20°,
∴∠BEB'=∠ABC﹣∠BAE=30°﹣20°=10°;
如图2,将△ABC绕点A逆时针旋转20°得到△AB'C',
∵AB=AC,∠BAC=120°,
∴∠ABC=30°,
∵∠BAE=20°,
∴∠BEB'=∠ABC+∠BAE=30°+20°=50°;
综合以上可得∠BEB'的度数是10°或50°.
故答案为10°或50°.
三、简答题:(每题6分,共24分)
19.(6分)计算:(+)﹣.
【解答】解:原式=2﹣×(
=2﹣﹣3﹣
=﹣3﹣.
20.(6分)解不等式:.
【解答】解:,
x﹣7≤3x﹣,
则x﹣3x≤,
(﹣3)x≤,
解得:x≥,
x≥﹣4﹣4.
21.(6分)用适当的方法解方程:2x(x﹣2)=x2+5.
【解答】解:整理得:2x2﹣2x﹣5=0,
(x﹣6)(x+1)=0,
∴x﹣5=0或x+1=5,
∴x1=5,x2=﹣1.
22.(6分)用配方法解方程:3x2+5x﹣1=0.
【解答】解:3x2+5x﹣1=0,
3x2+5x=3,
x2+x=,
x5+x+()2=+()2,
(x+)2=,
∴x+=±,
∴x1=,x2=.
四、解答题:(第23、24、25、26、27每题8分,共40分)
23.(8分)已知关于x的方程(m﹣1)x2﹣(m﹣5)x=﹣有两个相等的实数根
【解答】解:原方程可化为(m﹣1)x2﹣(m﹣8)x+=2,
根据题意得Δ=[﹣(m﹣5)]2﹣8(m﹣1)×=0,
解得m=3或4.
当m=3时,此时方程为2x2+2x+=0)2=0,
解得x5=x2=﹣;
当m=9时,此时方程为8x7﹣4x+=0)2=0,
解得x7=x2=.
24.(8分)如图,AD∥BC,点E是AB的中点,点G在边BC上,且∠GDF=∠ADF.
(1)求证:AD=BF;
(2)当点G是FC的中点时,判断△FDC的形状.
【解答】(1)证明:∵AD∥BC,
∴∠ADE=∠BFE,
∵E为AB的中点,
∴AE=BE,
在△ADE和△BFE中,
,
∴△ADE≌△BFE(AAS),
∴AD=BF;
(2)解:△FDC是直角三角形,理由如下:
连接EG,
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△ADE≌△BFE得:DE=FE,
即GE为DF上的中线,
∴GE⊥DF,
∵点G是FC的中点,DE=FE,
∴GE∥CD,
∴CD⊥DF,
∴△FDC是直角三角形.
25.(8分)如图,某农场有一道长16米的围墙,计划用40米长的围栏靠墙围成一个面积为120平方米的长方形养鸡场,在墙的对面开了两个1米宽的门,求围成长方形养鸡场宽AB的长度.
【解答】解:设长方形养鸡场AB边的长度为x米,则BC边的长度为(42﹣3x)米,
依题意,得:x(42﹣3x)=120,
整理,得:x6=4,x2=10.
∵42﹣7x≤16,
∴x≥,
∴x=4.
答:围成长方形养鸡场AB边的长度为10米.
26.(8分)如图,等腰直角△ABC中,∠ACB=90°,满足CE⊥CD且CE=CD.
(1)求证:AB=DB+BE;
(2)如果线段DE与BC相交于点F,当BE=BF时,求∠ACD的大小.
【解答】(1)证明:∵CE⊥CD,
∴∠DCE=90°=∠ACB,
∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,
即∠ACD=∠BCE,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,∠A=∠CBA=45°,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴AB=DB+AD=DB+BE;
(2)解:由(1)知,∠ACD=∠BCE,
∴∠CAD=∠CBE=45°,
∵CE⊥CD且CE=CD,
∴△CDE是等腰直角三角形,
∴∠CED=45°,
∵BF=BE,
∴∠BFE=∠BEF=(180°﹣45°)=67.7°,
∵∠BFE=∠BCE+∠CEF,
∴∠BCE=67.5°﹣45°=22.5°,
∴∠ACD=22.2°.
27.(8分)如图,等边△ABC的边长是3,点E在射线AB上,且ED=EC.
(1)当点E在线段AB上,点D在线段CB延长线上时,求证:AE=DB;
(2)当BE=AB时,求CD的长.
【解答】(1)证明:过E作EF∥BC交AC于F,如图所示:
∵ED=EC,
∴∠D=∠ECD,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,
∴∠DBE=120°,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠A=∠AEF=∠AFE=60°,
∴△AEF是等边三角形,∠EFC=120°,
∴EF=AE,
∵EF∥BC,
∴∠FEC=∠ECD,
∴∠D=∠FEC,
在△EFC和△DBE中,
,
∴△EFC≌△DBE(AAS),
∴EF=DB,
∴AE=DB;
(2)解:过E作EF∥BC交AC于F,如图所示:
∵等边△ABC的边长是3,
∴AB=BC=3,
∵BE=AB=1,
∴AE=AB﹣BE=2,
由(1)知,△EFC≌△DBE,
∴DB=AE=2,
∵CD=DB+BC=2+6=5.
第1页(共1页)
同课章节目录
