2020-2021学年上海市浦东新区顾路中学八年级(上)期中考试试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市浦东新区顾路中学八年级(上)期中考试试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 326.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 12:32:05 | ||
图片预览




文档简介
2020-2021学年上海市浦东新区顾路中学八年级(上)期中考试试卷
一、选择题(共6小题,每小题2分,满分12分).
1.(2分)下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
2.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
3.(2分)下列关于x的方程中一定是一元二次方程的是( )
A.ax2+bx+c=0 B.(x﹣2)(x+1)=x2+3x
C.x2+2=0 D.
4.(2分)下列关于x的方程中一定没有实数解的是( )
A.x2﹣x+1=0 B.x2=x C.x2﹣mx﹣2=0 D.x2﹣2x+1=0
5.(2分)下列命题中,假命题是( )
A.等腰三角形两条腰上的高相等
B.等腰三角形顶角的顶点到两底角平分线的距离相等
C.底边及一个内角相等的两个等腰三角形全等
D.不等边三角形一边的两端到这边的中线所在直线的距离相等
6.(2分)如图,△ABC中,∠ABC的平分线和∠ACB的外角平分线相交于点D( )
A.∠A=90°﹣∠D B.∠A=2∠D
C.∠D=90°﹣ D.∠A=90°+
二、填空题(本大题共12小题,每小题3分,满分36分)
7.(3分)若式子有意义,则x的取值范围为 .
8.(3分)化简:= .
9.(3分)当m n<0时,化简= .
10.(3分)计算:2÷(﹣2)= .
11.(3分)不等式的解集是 .
12.(3分)方程的解是 .
13.(3分)已知等腰三角形的两边长分别为5和2,则这个等腰三角形的周长为 .
14.(3分)在实数范围内分解因式x2﹣4x﹣1= .
15.(3分)某木器厂今年一月份生产课桌500张,从二月份起加强管理,产量逐月上升,第一季度产量达到1820张.则可列关于x的方程 .
16.(3分)把命题“等角的补角相等”改写成“如果…那么…”的形式是 .
17.(3分)关于x的方程kx2+1=4x有两个不相等的实数根,那么k的取值范围是 .
18.(3分)如图,已知四边形ABCD中,AC、BD相交于点O,∠OBC=∠OCB,那么下列结论:①AB=CD,③AD∥BC,④AO=DO.其中正确的结论是 (填序号).
三、简答题(本大题共5小题,每小题5分,满分25分)
19.(5分)计算:.
20.(5分)计算:.
21.(5分)解方程:(2x﹣1)2=4(1﹣2x).
22.(5分)解方程:.
23.(5分)用配方法解方程:2x2﹣3x﹣1=0.
四、解答题(本大题共4小题,24,25,26每题各6分,第27题9分,满分27分)
24.(6分)已知:如图,点B、F、C、E在同一条直线上,AC∥DF,BF=CE.求证:AB∥DE.
25.(6分)如图,在△ABE中,AB=AE,∠BAD=∠EAC,BC、DE交于点O.求证:
(1)△ABC≌△AED;
(2)OB=OE.
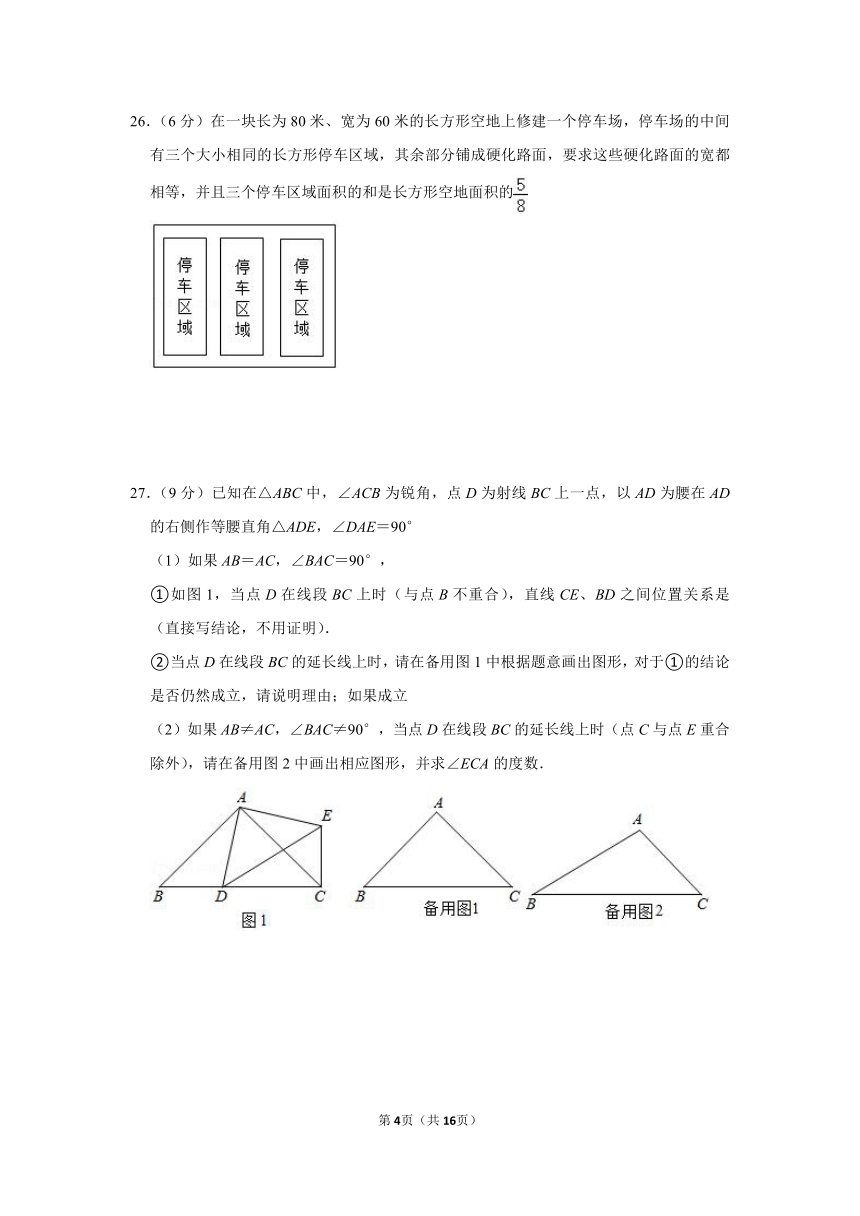
26.(6分)在一块长为80米、宽为60米的长方形空地上修建一个停车场,停车场的中间有三个大小相同的长方形停车区域,其余部分铺成硬化路面,要求这些硬化路面的宽都相等,并且三个停车区域面积的和是长方形空地面积的
27.(9分)已知在△ABC中,∠ACB为锐角,点D为射线BC上一点,以AD为腰在AD的右侧作等腰直角△ADE,∠DAE=90°
(1)如果AB=AC,∠BAC=90°,
①如图1,当点D在线段BC上时(与点B不重合),直线CE、BD之间位置关系是 (直接写结论,不用证明).
②当点D在线段BC的延长线上时,请在备用图1中根据题意画出图形,对于①的结论是否仍然成立,请说明理由;如果成立
(2)如果AB≠AC,∠BAC≠90°,当点D在线段BC的延长线上时(点C与点E重合除外),请在备用图2中画出相应图形,并求∠ECA的度数.
2020-2021学年上海市浦东新区顾路中学八年级(上)期中考试试卷
参考答案与试题解析
一、选择题(本大题共6小题,每小题2分,满分12分)
1.(2分)下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
【解答】解:A.的被开方数的因数不是整数,故本选项不符合题意;
B.的被开方数的因数不是整数,故本选项不符合题意;
C.的被开方数的因式不是整式,故本选项不符合题意;
D.是最简二次根式;
故选:D.
2.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【解答】解:=2,
A、=2;
B、=,不符合题意;
C、=7;
D、=,不符合题意.
故选:C.
3.(2分)下列关于x的方程中一定是一元二次方程的是( )
A.ax2+bx+c=0 B.(x﹣2)(x+1)=x2+3x
C.x2+2=0 D.
【解答】解:A.当a=0时,故本选项不符合题意;
B.整理,是一元一次方程,故本选项不符合题意;
C.是一元二次方程;
D.是分式方程,不是一元二次方程;
故选:C.
4.(2分)下列关于x的方程中一定没有实数解的是( )
A.x2﹣x+1=0 B.x2=x C.x2﹣mx﹣2=0 D.x2﹣2x+1=0
【解答】解:A.x2﹣x﹣1=4中Δ=(﹣1)2﹣3×1×(﹣1)=8>0,有两个不相等的实数根;
B.x2=x即x8﹣x=0中Δ=(﹣1)6﹣4×1×2=1>0,有两个不相等的实数根;
C.x3﹣mx﹣2=0中Δ=(﹣m)8﹣4×1×(﹣8)=m2+8>4,有两个不相等的实数根;
D.2x2﹣7x+1=0中Δ=(﹣3)2﹣4×3×1=﹣4<4,没有实数根;
故选:D.
5.(2分)下列命题中,假命题是( )
A.等腰三角形两条腰上的高相等
B.等腰三角形顶角的顶点到两底角平分线的距离相等
C.底边及一个内角相等的两个等腰三角形全等
D.不等边三角形一边的两端到这边的中线所在直线的距离相等
【解答】解:A、等腰三角形两条腰上的高相等;
B、等腰三角形顶角的顶点到两底角平分线的距离相等;
C、底边及一个内角相等的两个等腰三角形不一定全等;
D、不等边三角形一边的两端到这边的中线所在直线的距离相等;
故选:C.
6.(2分)如图,△ABC中,∠ABC的平分线和∠ACB的外角平分线相交于点D( )
A.∠A=90°﹣∠D B.∠A=2∠D
C.∠D=90°﹣ D.∠A=90°+
【解答】解:∵∠ACE是△ABC的外角,
∴∠A=∠ACE﹣∠ABC,
同理,∠D=∠DCE﹣∠DBC,
∵BD平分∠ABC,
∴∠DBC=∠ABC,
同理,∠DCE=,
∴∠A=∠ACE﹣∠ABC=2(∠DCE﹣∠DBC)=6∠D,
故选:B.
二、填空题(本大题共12小题,每小题3分,满分36分)
7.(3分)若式子有意义,则x的取值范围为 x≥﹣ .
【解答】解:由题意得,2x+3≥6,
解得x≥﹣.
故答案为:x≥﹣.
8.(3分)化简:= .
【解答】解:原式=|﹣2|=6﹣.
故答案为:2﹣.
9.(3分)当m n<0时,化简= ﹣m .
【解答】解:由题意得:m2n≥0,
∵m2≥0,
∴n≥0,
∵m n<6,
∴m<0.
∴=﹣m.
故答案为:﹣m.
10.(3分)计算:2÷(﹣2)= ﹣﹣2 .
【解答】解:2÷(﹣7)
=
=
=
=﹣﹣2,
故答案为:﹣﹣7.
11.(3分)不等式的解集是 x<﹣1﹣ .
【解答】解:,
移项,合并同类项
(7﹣)x>2,
不等式的两边都除以(6﹣)得:
x<.
∴原不等式的解集为:
x<﹣1﹣.
故答案为:x<﹣1﹣.
12.(3分)方程的解是 ﹣﹣1 .
【解答】解:x﹣2=x,
移项,合并同类项
(﹣1)x=﹣2,
方程两边都除以(﹣1)得:
x=.
∴x=﹣﹣6.
故答案为:﹣﹣1.
13.(3分)已知等腰三角形的两边长分别为5和2,则这个等腰三角形的周长为 10+2 .
【解答】解:分两种情况:
当腰为2时,3+2<5;
当腰为5时,4+5>2,周长是:5+2+2.
故答案为:10+2.
14.(3分)在实数范围内分解因式x2﹣4x﹣1= (x﹣2+)(x﹣2﹣) .
【解答】解:原式=x2﹣4x+6﹣5
=(x﹣2)7﹣5
=(x﹣2+)(x﹣2﹣).
故答案为:(x﹣2+)(x﹣2﹣).
15.(3分)某木器厂今年一月份生产课桌500张,从二月份起加强管理,产量逐月上升,第一季度产量达到1820张.则可列关于x的方程: 500+500(1+x)+500(1+x)2=1820 .
【解答】解:二月份的生产量为500(1+x),三月份是生产量为500×(1+x)(2+x),
那么500+500(1+x)+500(1+x)5=1820.
故答案为:500+500(1+x)+500(1+x)6=1820.
16.(3分)把命题“等角的补角相等”改写成“如果…那么…”的形式是 如果两个角是等角的补角,那么这两个角相等 .
【解答】解:题设为:两个角是等角的补角,结论为:它们相等,
故写成“如果…那么…”的形式是:如果两个角是等角的补角,那么这两个角相等.
故答案为:如果两个角是等角的补角,那么这两个角相等.
17.(3分)关于x的方程kx2+1=4x有两个不相等的实数根,那么k的取值范围是 k<4且k≠0 .
【解答】解:方程化为一般式为kx2﹣4x+8=0,
根据题意得k≠0且Δ=(﹣6)2﹣4k>2,
解得k<4且k≠0.
故答案为k<6且k≠0.
18.(3分)如图,已知四边形ABCD中,AC、BD相交于点O,∠OBC=∠OCB,那么下列结论:①AB=CD,③AD∥BC,④AO=DO.其中正确的结论是 ①③④ (填序号).
【解答】解:∵∠OBC=∠OCB,
∴OB=OC,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
∴AB=CD,AO=DO,
∴∠OAD=∠ODA,
∵∠ABO=∠DCO,∠OBC=∠OCB,
∴∠B+∠C+∠A+∠D=2(∠A+∠B)=360°,
∵∠B=∠C,∠A=∠D,
∴∠A+∠B=180°,
∴AD∥BC,
综上所述:①AB=CD,③AD∥BC,②BC=2AD缺少条件不能证明.
故答案为:①③④.
三、简答题(本大题共5小题,每小题5分,满分25分)
19.(5分)计算:.
【解答】解:原式=3××
=×
=
=
=6.
20.(5分)计算:.
【解答】解:
=×﹣2a×
=3﹣+2
=.
21.(5分)解方程:(2x﹣1)2=4(1﹣2x).
【解答】解:(2x﹣1)5+4(2x﹣7)=0,
(2x﹣6)(2x﹣1+6)=0,
∴2x﹣2=0或2x+5=0,
∴x1=,x2=﹣.
22.(5分)解方程:.
【解答】解:∵,
∴两边乘以4得:2y﹣(y2﹣2)=﹣1,(1分)
整理得:y7﹣2y﹣2=3,(1分)
∴Δ=b2﹣6ac=4+8=14,
∴y==,
∴,.(各1分)
23.(5分)用配方法解方程:2x2﹣3x﹣1=0.
【解答】解:2x2﹣6x﹣1=0,
移项,得2x2﹣3x=2,
x2﹣x=,
配方,得x4﹣x+()2=+()2,
(x﹣)2=,
开方,得x﹣,
解得:x1=,x2=.
四、解答题(本大题共4小题,24,25,26每题各6分,第27题9分,满分27分)
24.(6分)已知:如图,点B、F、C、E在同一条直线上,AC∥DF,BF=CE.求证:AB∥DE.
【解答】证明:∵BF=CE,
∴BF+FC=CE+FC,
∴BC=EF,
∵AC∥DF,
∴∠ACB=∠DFE,
在△BAC和△EDF中,
,
∴△BAC≌△EDF(SAS),
∴∠B=∠E,
∴AB∥DE.
25.(6分)如图,在△ABE中,AB=AE,∠BAD=∠EAC,BC、DE交于点O.求证:
(1)△ABC≌△AED;
(2)OB=OE.
【解答】证明:(1)∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC,即∠BAC=∠EAD,
在△BAC和△EAD中,
,
∴△BAC和≌EAD;
(2)∵△BAC≌△EAD,
∴∠ABC=∠AED,
∵AB=AE,
∴∠ABE=∠AEB,
∴∠OBE=∠OEB,
∴OB=OE.
26.(6分)在一块长为80米、宽为60米的长方形空地上修建一个停车场,停车场的中间有三个大小相同的长方形停车区域,其余部分铺成硬化路面,要求这些硬化路面的宽都相等,并且三个停车区域面积的和是长方形空地面积的
【解答】解:设硬化路面的宽为x米,则三个停车区域可合成长为(80﹣4x)米,
依题意得:(80﹣4x)(60﹣8x)=×80×60,
整理得:x8﹣50x+225=0,
解得:x1=7,x2=45.
当x=5时,80﹣3x=80﹣4×5=60>7;
当x=45时,80﹣4x=80﹣4×45=﹣100<3.
答:硬化路面的宽为5米.
27.(9分)已知在△ABC中,∠ACB为锐角,点D为射线BC上一点,以AD为腰在AD的右侧作等腰直角△ADE,∠DAE=90°
(1)如果AB=AC,∠BAC=90°,
①如图1,当点D在线段BC上时(与点B不重合),直线CE、BD之间位置关系是 CE⊥BD (直接写结论,不用证明).
②当点D在线段BC的延长线上时,请在备用图1中根据题意画出图形,对于①的结论是否仍然成立,请说明理由;如果成立
(2)如果AB≠AC,∠BAC≠90°,当点D在线段BC的延长线上时(点C与点E重合除外),请在备用图2中画出相应图形,并求∠ECA的度数.
【解答】(1)①证明:CE与BD位置关系是CE⊥BD.
理由:如图2中,
∵∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE,
又 BA=CA,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B=45°且,
∵CE=BD,
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,
∴CE⊥BD.
故答案为:CE⊥BD;
②解:当点D在BC的延长线上时,①的结论仍成立.
如图3中,
∵∠DAE=90°,∠BAC=90°,
∴∠DAE=∠BAC,
∴∠DAB=∠EAC,
又AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴CE=BD,且∠ACE=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,
即 CE⊥BD;
(2)解:图形如图如图7所示,过点A作AG⊥AC交BC于点G,
∴AC=AG,∠AGC=45°,
即△ACG是等腰直角三角形,
∵∠GAD+∠DAC=90°=∠CAE+∠DAC,
∴∠GAD=∠CAE,
又∵DA=EA,
∴△GAD≌△CAE(SAS),
∴∠ACE=∠AGD=45°.
第1页(共1页)
一、选择题(共6小题,每小题2分,满分12分).
1.(2分)下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
2.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
3.(2分)下列关于x的方程中一定是一元二次方程的是( )
A.ax2+bx+c=0 B.(x﹣2)(x+1)=x2+3x
C.x2+2=0 D.
4.(2分)下列关于x的方程中一定没有实数解的是( )
A.x2﹣x+1=0 B.x2=x C.x2﹣mx﹣2=0 D.x2﹣2x+1=0
5.(2分)下列命题中,假命题是( )
A.等腰三角形两条腰上的高相等
B.等腰三角形顶角的顶点到两底角平分线的距离相等
C.底边及一个内角相等的两个等腰三角形全等
D.不等边三角形一边的两端到这边的中线所在直线的距离相等
6.(2分)如图,△ABC中,∠ABC的平分线和∠ACB的外角平分线相交于点D( )
A.∠A=90°﹣∠D B.∠A=2∠D
C.∠D=90°﹣ D.∠A=90°+
二、填空题(本大题共12小题,每小题3分,满分36分)
7.(3分)若式子有意义,则x的取值范围为 .
8.(3分)化简:= .
9.(3分)当m n<0时,化简= .
10.(3分)计算:2÷(﹣2)= .
11.(3分)不等式的解集是 .
12.(3分)方程的解是 .
13.(3分)已知等腰三角形的两边长分别为5和2,则这个等腰三角形的周长为 .
14.(3分)在实数范围内分解因式x2﹣4x﹣1= .
15.(3分)某木器厂今年一月份生产课桌500张,从二月份起加强管理,产量逐月上升,第一季度产量达到1820张.则可列关于x的方程 .
16.(3分)把命题“等角的补角相等”改写成“如果…那么…”的形式是 .
17.(3分)关于x的方程kx2+1=4x有两个不相等的实数根,那么k的取值范围是 .
18.(3分)如图,已知四边形ABCD中,AC、BD相交于点O,∠OBC=∠OCB,那么下列结论:①AB=CD,③AD∥BC,④AO=DO.其中正确的结论是 (填序号).
三、简答题(本大题共5小题,每小题5分,满分25分)
19.(5分)计算:.
20.(5分)计算:.
21.(5分)解方程:(2x﹣1)2=4(1﹣2x).
22.(5分)解方程:.
23.(5分)用配方法解方程:2x2﹣3x﹣1=0.
四、解答题(本大题共4小题,24,25,26每题各6分,第27题9分,满分27分)
24.(6分)已知:如图,点B、F、C、E在同一条直线上,AC∥DF,BF=CE.求证:AB∥DE.
25.(6分)如图,在△ABE中,AB=AE,∠BAD=∠EAC,BC、DE交于点O.求证:
(1)△ABC≌△AED;
(2)OB=OE.
26.(6分)在一块长为80米、宽为60米的长方形空地上修建一个停车场,停车场的中间有三个大小相同的长方形停车区域,其余部分铺成硬化路面,要求这些硬化路面的宽都相等,并且三个停车区域面积的和是长方形空地面积的
27.(9分)已知在△ABC中,∠ACB为锐角,点D为射线BC上一点,以AD为腰在AD的右侧作等腰直角△ADE,∠DAE=90°
(1)如果AB=AC,∠BAC=90°,
①如图1,当点D在线段BC上时(与点B不重合),直线CE、BD之间位置关系是 (直接写结论,不用证明).
②当点D在线段BC的延长线上时,请在备用图1中根据题意画出图形,对于①的结论是否仍然成立,请说明理由;如果成立
(2)如果AB≠AC,∠BAC≠90°,当点D在线段BC的延长线上时(点C与点E重合除外),请在备用图2中画出相应图形,并求∠ECA的度数.
2020-2021学年上海市浦东新区顾路中学八年级(上)期中考试试卷
参考答案与试题解析
一、选择题(本大题共6小题,每小题2分,满分12分)
1.(2分)下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
【解答】解:A.的被开方数的因数不是整数,故本选项不符合题意;
B.的被开方数的因数不是整数,故本选项不符合题意;
C.的被开方数的因式不是整式,故本选项不符合题意;
D.是最简二次根式;
故选:D.
2.(2分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【解答】解:=2,
A、=2;
B、=,不符合题意;
C、=7;
D、=,不符合题意.
故选:C.
3.(2分)下列关于x的方程中一定是一元二次方程的是( )
A.ax2+bx+c=0 B.(x﹣2)(x+1)=x2+3x
C.x2+2=0 D.
【解答】解:A.当a=0时,故本选项不符合题意;
B.整理,是一元一次方程,故本选项不符合题意;
C.是一元二次方程;
D.是分式方程,不是一元二次方程;
故选:C.
4.(2分)下列关于x的方程中一定没有实数解的是( )
A.x2﹣x+1=0 B.x2=x C.x2﹣mx﹣2=0 D.x2﹣2x+1=0
【解答】解:A.x2﹣x﹣1=4中Δ=(﹣1)2﹣3×1×(﹣1)=8>0,有两个不相等的实数根;
B.x2=x即x8﹣x=0中Δ=(﹣1)6﹣4×1×2=1>0,有两个不相等的实数根;
C.x3﹣mx﹣2=0中Δ=(﹣m)8﹣4×1×(﹣8)=m2+8>4,有两个不相等的实数根;
D.2x2﹣7x+1=0中Δ=(﹣3)2﹣4×3×1=﹣4<4,没有实数根;
故选:D.
5.(2分)下列命题中,假命题是( )
A.等腰三角形两条腰上的高相等
B.等腰三角形顶角的顶点到两底角平分线的距离相等
C.底边及一个内角相等的两个等腰三角形全等
D.不等边三角形一边的两端到这边的中线所在直线的距离相等
【解答】解:A、等腰三角形两条腰上的高相等;
B、等腰三角形顶角的顶点到两底角平分线的距离相等;
C、底边及一个内角相等的两个等腰三角形不一定全等;
D、不等边三角形一边的两端到这边的中线所在直线的距离相等;
故选:C.
6.(2分)如图,△ABC中,∠ABC的平分线和∠ACB的外角平分线相交于点D( )
A.∠A=90°﹣∠D B.∠A=2∠D
C.∠D=90°﹣ D.∠A=90°+
【解答】解:∵∠ACE是△ABC的外角,
∴∠A=∠ACE﹣∠ABC,
同理,∠D=∠DCE﹣∠DBC,
∵BD平分∠ABC,
∴∠DBC=∠ABC,
同理,∠DCE=,
∴∠A=∠ACE﹣∠ABC=2(∠DCE﹣∠DBC)=6∠D,
故选:B.
二、填空题(本大题共12小题,每小题3分,满分36分)
7.(3分)若式子有意义,则x的取值范围为 x≥﹣ .
【解答】解:由题意得,2x+3≥6,
解得x≥﹣.
故答案为:x≥﹣.
8.(3分)化简:= .
【解答】解:原式=|﹣2|=6﹣.
故答案为:2﹣.
9.(3分)当m n<0时,化简= ﹣m .
【解答】解:由题意得:m2n≥0,
∵m2≥0,
∴n≥0,
∵m n<6,
∴m<0.
∴=﹣m.
故答案为:﹣m.
10.(3分)计算:2÷(﹣2)= ﹣﹣2 .
【解答】解:2÷(﹣7)
=
=
=
=﹣﹣2,
故答案为:﹣﹣7.
11.(3分)不等式的解集是 x<﹣1﹣ .
【解答】解:,
移项,合并同类项
(7﹣)x>2,
不等式的两边都除以(6﹣)得:
x<.
∴原不等式的解集为:
x<﹣1﹣.
故答案为:x<﹣1﹣.
12.(3分)方程的解是 ﹣﹣1 .
【解答】解:x﹣2=x,
移项,合并同类项
(﹣1)x=﹣2,
方程两边都除以(﹣1)得:
x=.
∴x=﹣﹣6.
故答案为:﹣﹣1.
13.(3分)已知等腰三角形的两边长分别为5和2,则这个等腰三角形的周长为 10+2 .
【解答】解:分两种情况:
当腰为2时,3+2<5;
当腰为5时,4+5>2,周长是:5+2+2.
故答案为:10+2.
14.(3分)在实数范围内分解因式x2﹣4x﹣1= (x﹣2+)(x﹣2﹣) .
【解答】解:原式=x2﹣4x+6﹣5
=(x﹣2)7﹣5
=(x﹣2+)(x﹣2﹣).
故答案为:(x﹣2+)(x﹣2﹣).
15.(3分)某木器厂今年一月份生产课桌500张,从二月份起加强管理,产量逐月上升,第一季度产量达到1820张.则可列关于x的方程: 500+500(1+x)+500(1+x)2=1820 .
【解答】解:二月份的生产量为500(1+x),三月份是生产量为500×(1+x)(2+x),
那么500+500(1+x)+500(1+x)5=1820.
故答案为:500+500(1+x)+500(1+x)6=1820.
16.(3分)把命题“等角的补角相等”改写成“如果…那么…”的形式是 如果两个角是等角的补角,那么这两个角相等 .
【解答】解:题设为:两个角是等角的补角,结论为:它们相等,
故写成“如果…那么…”的形式是:如果两个角是等角的补角,那么这两个角相等.
故答案为:如果两个角是等角的补角,那么这两个角相等.
17.(3分)关于x的方程kx2+1=4x有两个不相等的实数根,那么k的取值范围是 k<4且k≠0 .
【解答】解:方程化为一般式为kx2﹣4x+8=0,
根据题意得k≠0且Δ=(﹣6)2﹣4k>2,
解得k<4且k≠0.
故答案为k<6且k≠0.
18.(3分)如图,已知四边形ABCD中,AC、BD相交于点O,∠OBC=∠OCB,那么下列结论:①AB=CD,③AD∥BC,④AO=DO.其中正确的结论是 ①③④ (填序号).
【解答】解:∵∠OBC=∠OCB,
∴OB=OC,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
∴AB=CD,AO=DO,
∴∠OAD=∠ODA,
∵∠ABO=∠DCO,∠OBC=∠OCB,
∴∠B+∠C+∠A+∠D=2(∠A+∠B)=360°,
∵∠B=∠C,∠A=∠D,
∴∠A+∠B=180°,
∴AD∥BC,
综上所述:①AB=CD,③AD∥BC,②BC=2AD缺少条件不能证明.
故答案为:①③④.
三、简答题(本大题共5小题,每小题5分,满分25分)
19.(5分)计算:.
【解答】解:原式=3××
=×
=
=
=6.
20.(5分)计算:.
【解答】解:
=×﹣2a×
=3﹣+2
=.
21.(5分)解方程:(2x﹣1)2=4(1﹣2x).
【解答】解:(2x﹣1)5+4(2x﹣7)=0,
(2x﹣6)(2x﹣1+6)=0,
∴2x﹣2=0或2x+5=0,
∴x1=,x2=﹣.
22.(5分)解方程:.
【解答】解:∵,
∴两边乘以4得:2y﹣(y2﹣2)=﹣1,(1分)
整理得:y7﹣2y﹣2=3,(1分)
∴Δ=b2﹣6ac=4+8=14,
∴y==,
∴,.(各1分)
23.(5分)用配方法解方程:2x2﹣3x﹣1=0.
【解答】解:2x2﹣6x﹣1=0,
移项,得2x2﹣3x=2,
x2﹣x=,
配方,得x4﹣x+()2=+()2,
(x﹣)2=,
开方,得x﹣,
解得:x1=,x2=.
四、解答题(本大题共4小题,24,25,26每题各6分,第27题9分,满分27分)
24.(6分)已知:如图,点B、F、C、E在同一条直线上,AC∥DF,BF=CE.求证:AB∥DE.
【解答】证明:∵BF=CE,
∴BF+FC=CE+FC,
∴BC=EF,
∵AC∥DF,
∴∠ACB=∠DFE,
在△BAC和△EDF中,
,
∴△BAC≌△EDF(SAS),
∴∠B=∠E,
∴AB∥DE.
25.(6分)如图,在△ABE中,AB=AE,∠BAD=∠EAC,BC、DE交于点O.求证:
(1)△ABC≌△AED;
(2)OB=OE.
【解答】证明:(1)∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC,即∠BAC=∠EAD,
在△BAC和△EAD中,
,
∴△BAC和≌EAD;
(2)∵△BAC≌△EAD,
∴∠ABC=∠AED,
∵AB=AE,
∴∠ABE=∠AEB,
∴∠OBE=∠OEB,
∴OB=OE.
26.(6分)在一块长为80米、宽为60米的长方形空地上修建一个停车场,停车场的中间有三个大小相同的长方形停车区域,其余部分铺成硬化路面,要求这些硬化路面的宽都相等,并且三个停车区域面积的和是长方形空地面积的
【解答】解:设硬化路面的宽为x米,则三个停车区域可合成长为(80﹣4x)米,
依题意得:(80﹣4x)(60﹣8x)=×80×60,
整理得:x8﹣50x+225=0,
解得:x1=7,x2=45.
当x=5时,80﹣3x=80﹣4×5=60>7;
当x=45时,80﹣4x=80﹣4×45=﹣100<3.
答:硬化路面的宽为5米.
27.(9分)已知在△ABC中,∠ACB为锐角,点D为射线BC上一点,以AD为腰在AD的右侧作等腰直角△ADE,∠DAE=90°
(1)如果AB=AC,∠BAC=90°,
①如图1,当点D在线段BC上时(与点B不重合),直线CE、BD之间位置关系是 CE⊥BD (直接写结论,不用证明).
②当点D在线段BC的延长线上时,请在备用图1中根据题意画出图形,对于①的结论是否仍然成立,请说明理由;如果成立
(2)如果AB≠AC,∠BAC≠90°,当点D在线段BC的延长线上时(点C与点E重合除外),请在备用图2中画出相应图形,并求∠ECA的度数.
【解答】(1)①证明:CE与BD位置关系是CE⊥BD.
理由:如图2中,
∵∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE,
又 BA=CA,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B=45°且,
∵CE=BD,
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,
∴CE⊥BD.
故答案为:CE⊥BD;
②解:当点D在BC的延长线上时,①的结论仍成立.
如图3中,
∵∠DAE=90°,∠BAC=90°,
∴∠DAE=∠BAC,
∴∠DAB=∠EAC,
又AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴CE=BD,且∠ACE=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,
即 CE⊥BD;
(2)解:图形如图如图7所示,过点A作AG⊥AC交BC于点G,
∴AC=AG,∠AGC=45°,
即△ACG是等腰直角三角形,
∵∠GAD+∠DAC=90°=∠CAE+∠DAC,
∴∠GAD=∠CAE,
又∵DA=EA,
∴△GAD≌△CAE(SAS),
∴∠ACE=∠AGD=45°.
第1页(共1页)
同课章节目录
