5.6.1应用一元一次方程——追赶小明(共23张PPT)
文档属性
| 名称 | 5.6.1应用一元一次方程——追赶小明(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 57.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 12:17:05 | ||
图片预览






文档简介
(共23张PPT)
5.6应用一元一次方程
——追赶小明
北师大版 七年级上
学习目标
1.借助“线段图”分析追及问题和复杂行程问题中的等量关系,建立方程解应用题;
2.提高分析问题,解决问题的能力,进一步体会方程模型的思想;
3.发展文字语言、图形语言、符号语言之间的转换能力。
能追上小明吗?
1.若小明每秒跑4米,那么他5秒能跑____米
2.小明用4分钟绕学校操场跑了两圈(每圈400米)那么他的速度是____米/分.
3.已知小明家距离火车站800米,他以4米/秒的速度骑车到达车站需要____秒.
路程=速度×时间
速度=路程÷时间
时间=路程÷速度
20
200
200
复习导入
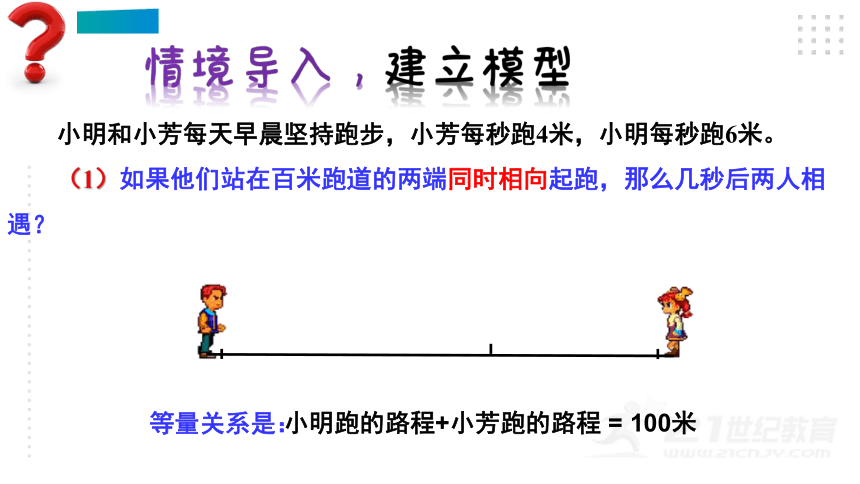
小明和小芳每天早晨坚持跑步,小芳每秒跑4米,小明每秒跑6米。
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
等量关系是:
小明跑的路程+小芳跑的路程 = 100米
情境导入,建立模型
解:设x秒后两人能相遇,依题意列方程,得
4x + 6x = 100
解得: x=10
答:经过10秒后两人能相遇。
情境导入,建立模型
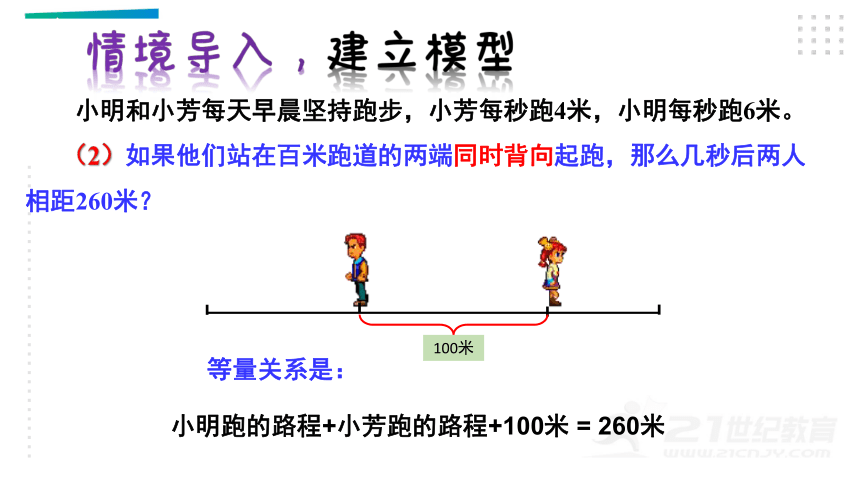
小明和小芳每天早晨坚持跑步,小芳每秒跑4米,小明每秒跑6米。
(2)如果他们站在百米跑道的两端同时背向起跑,那么几秒后两人相距260米?
等量关系是:
小明跑的路程+小芳跑的路程+100米 = 260米
100米
情境导入,建立模型
解:设x秒后两人相距260米,依题意列方程,得
4x + 6x +100= 260
解得: x=16
答:经过16秒后两人相距260米。
情境导入,建立模型
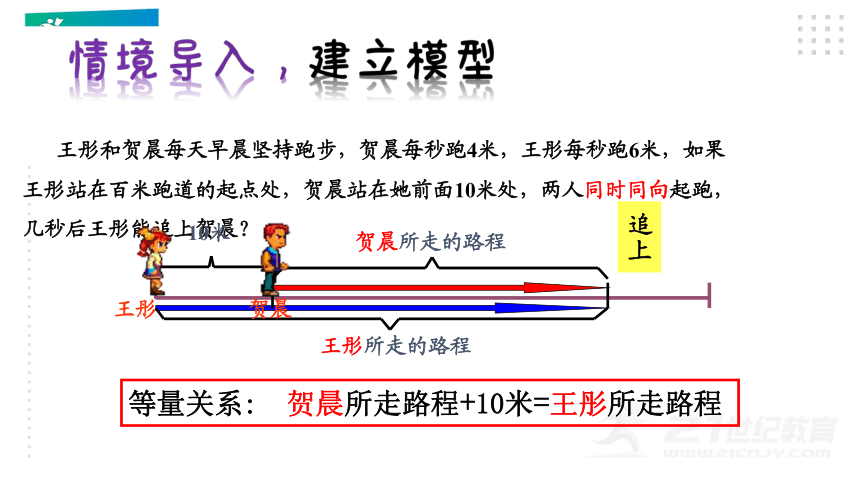
王彤和贺晨每天早晨坚持跑步,贺晨每秒跑4米,王彤每秒跑6米,如果王彤站在百米跑道的起点处,贺晨站在她前面10米处,两人同时同向起跑,几秒后王彤能追上贺晨?
10米
贺晨所走的路程
王彤所走的路程
王彤
贺晨
追上
等量关系: 贺晨所走路程+10米=王彤所走路程
情境导入,建立模型
等量关系: 贺晨所走路程+10米=王彤所走路程
王彤和贺晨每天早晨坚持跑步,贺晨每秒跑4米,王彤每秒跑6米,如果王彤站在百米跑道的起点处,贺晨站在她前面10米处,两人同时同向起跑,几秒后王彤能追上贺晨?
设x秒后王彤能追上贺晨,根据题意,得
4x+10=6x
化简,得 2x=10
x =5
答:两人同时同向同跑,5秒后王彤能追上贺晨.
解:
情境导入,建立模型
80×5
80x
小明每天早上要在7:50之前赶到距家1000米的学校上学。小明以80米/分的速度出发,5分钟后,小明的爸爸发现她忘了带数学书。于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了她。
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
180x
家
学校
A B C
新课讲解
解:(1)设爸爸追上小明用了x分,根据题意,得
180x=80x+80×5
化简,得 100x=400
x=4
因此,爸爸追上小明用了4分。
(2)因为 180 ×4=720(米)
1000-720=280(米)
所以,追上小明时,距离学校还有280米。
育红学校七年级学生步行到郊外旅行。七(1)班学生组成前队,步行速度为4千米/时,七(2)班学生组成后队,速度为6千米/时。前队出发一小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
根据上面的事实提出问题,并尝试解答.
议一议
联络员第一次追上前队时用了多长时间?
解:设联络员追上前队用了x小时,
根据题意,得:
12x = 4x + 4
解得:x =0.5
答:联络员追上前队时用了0.5小时。
后队追上前队时用了多长时间?
解:设后队追上前队用了x小时,
根据题意,得:
6x = 4x + 4
答:后队追上前队时用了2小时。
解得:x = 2
1.小彬和小强每天早晨坚持跑步,小彬每秒跑4m,小强每秒跑6m.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇
(2)如果小强站在百米跑道的起点处,小彬站在他前面10m处,两人同时同向起跑,几秒后小强能追上小彬
当堂测试
解∶(1)设x秒后两人相遇,则小强跑了6x m,小彬跑了4xm,
根据题意,得6x+4x=100,
解得 x=10.
答∶10秒后两人相遇;
(2)设y秒后小强追上小彬,
根据题意,得6y-4y=10,
解得 y=5.
答∶5秒后小强能追上小彬.
2.一个自行车队进行训练,训练时所有队员都以35 km/h的速度前进。突然,1号队员以 45 km/h的速度独自行进,行进10 km后掉转车头,仍以 45 km/h的速度往回骑,直到与其他队员会合.1号队员从离队开始到与队员重新会合,经过了多长时间
当堂测试
解:设1号队员从离队开始到与队员重新会合经过了xh.
根据题意,得45x +35x=10×2.解得x=
答∶1号队员从离队开始到与队员重新会合经过了小时·
实际问题
数学问题
已知量、未知量、 等量关系
方程
方程的解
解的合理性
解释
运用方程解决实际问题的思维步骤:
抽象
验证
合理
求解
列出
分析
不合理
课堂小结
学生以组为单位讨论交流一下,本节课的收获和感受。然后组长提交反馈表。
https://www.21cnjy.com/help/help_extract.php
5.6应用一元一次方程
——追赶小明
北师大版 七年级上
学习目标
1.借助“线段图”分析追及问题和复杂行程问题中的等量关系,建立方程解应用题;
2.提高分析问题,解决问题的能力,进一步体会方程模型的思想;
3.发展文字语言、图形语言、符号语言之间的转换能力。
能追上小明吗?
1.若小明每秒跑4米,那么他5秒能跑____米
2.小明用4分钟绕学校操场跑了两圈(每圈400米)那么他的速度是____米/分.
3.已知小明家距离火车站800米,他以4米/秒的速度骑车到达车站需要____秒.
路程=速度×时间
速度=路程÷时间
时间=路程÷速度
20
200
200
复习导入
小明和小芳每天早晨坚持跑步,小芳每秒跑4米,小明每秒跑6米。
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
等量关系是:
小明跑的路程+小芳跑的路程 = 100米
情境导入,建立模型
解:设x秒后两人能相遇,依题意列方程,得
4x + 6x = 100
解得: x=10
答:经过10秒后两人能相遇。
情境导入,建立模型
小明和小芳每天早晨坚持跑步,小芳每秒跑4米,小明每秒跑6米。
(2)如果他们站在百米跑道的两端同时背向起跑,那么几秒后两人相距260米?
等量关系是:
小明跑的路程+小芳跑的路程+100米 = 260米
100米
情境导入,建立模型
解:设x秒后两人相距260米,依题意列方程,得
4x + 6x +100= 260
解得: x=16
答:经过16秒后两人相距260米。
情境导入,建立模型
王彤和贺晨每天早晨坚持跑步,贺晨每秒跑4米,王彤每秒跑6米,如果王彤站在百米跑道的起点处,贺晨站在她前面10米处,两人同时同向起跑,几秒后王彤能追上贺晨?
10米
贺晨所走的路程
王彤所走的路程
王彤
贺晨
追上
等量关系: 贺晨所走路程+10米=王彤所走路程
情境导入,建立模型
等量关系: 贺晨所走路程+10米=王彤所走路程
王彤和贺晨每天早晨坚持跑步,贺晨每秒跑4米,王彤每秒跑6米,如果王彤站在百米跑道的起点处,贺晨站在她前面10米处,两人同时同向起跑,几秒后王彤能追上贺晨?
设x秒后王彤能追上贺晨,根据题意,得
4x+10=6x
化简,得 2x=10
x =5
答:两人同时同向同跑,5秒后王彤能追上贺晨.
解:
情境导入,建立模型
80×5
80x
小明每天早上要在7:50之前赶到距家1000米的学校上学。小明以80米/分的速度出发,5分钟后,小明的爸爸发现她忘了带数学书。于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了她。
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
180x
家
学校
A B C
新课讲解
解:(1)设爸爸追上小明用了x分,根据题意,得
180x=80x+80×5
化简,得 100x=400
x=4
因此,爸爸追上小明用了4分。
(2)因为 180 ×4=720(米)
1000-720=280(米)
所以,追上小明时,距离学校还有280米。
育红学校七年级学生步行到郊外旅行。七(1)班学生组成前队,步行速度为4千米/时,七(2)班学生组成后队,速度为6千米/时。前队出发一小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
根据上面的事实提出问题,并尝试解答.
议一议
联络员第一次追上前队时用了多长时间?
解:设联络员追上前队用了x小时,
根据题意,得:
12x = 4x + 4
解得:x =0.5
答:联络员追上前队时用了0.5小时。
后队追上前队时用了多长时间?
解:设后队追上前队用了x小时,
根据题意,得:
6x = 4x + 4
答:后队追上前队时用了2小时。
解得:x = 2
1.小彬和小强每天早晨坚持跑步,小彬每秒跑4m,小强每秒跑6m.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇
(2)如果小强站在百米跑道的起点处,小彬站在他前面10m处,两人同时同向起跑,几秒后小强能追上小彬
当堂测试
解∶(1)设x秒后两人相遇,则小强跑了6x m,小彬跑了4xm,
根据题意,得6x+4x=100,
解得 x=10.
答∶10秒后两人相遇;
(2)设y秒后小强追上小彬,
根据题意,得6y-4y=10,
解得 y=5.
答∶5秒后小强能追上小彬.
2.一个自行车队进行训练,训练时所有队员都以35 km/h的速度前进。突然,1号队员以 45 km/h的速度独自行进,行进10 km后掉转车头,仍以 45 km/h的速度往回骑,直到与其他队员会合.1号队员从离队开始到与队员重新会合,经过了多长时间
当堂测试
解:设1号队员从离队开始到与队员重新会合经过了xh.
根据题意,得45x +35x=10×2.解得x=
答∶1号队员从离队开始到与队员重新会合经过了小时·
实际问题
数学问题
已知量、未知量、 等量关系
方程
方程的解
解的合理性
解释
运用方程解决实际问题的思维步骤:
抽象
验证
合理
求解
列出
分析
不合理
课堂小结
学生以组为单位讨论交流一下,本节课的收获和感受。然后组长提交反馈表。
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
