12.3角的平分线的性质基础达标训练题--2021--2022学年人教版(2012)八年级上册数学(word版含答案)
文档属性
| 名称 | 12.3角的平分线的性质基础达标训练题--2021--2022学年人教版(2012)八年级上册数学(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 499.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 17:25:38 | ||
图片预览


文档简介
12.3角的平分线的性质基础达标训练题--2021--2022学年人教版(2012)八年级上学期
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.到△ABC的三边距离相等的点是△ABC的( )
A.三边中线的交点 B.三条角平分线的交点 C.三边上高的交点 D.三边垂直平分线的交点
2.如图,在Rt△ABC中,∠C=90°,AD是∠BAC平分线,DE⊥AB,垂足为E,若CD=10,则DE的长度为( )
A. B. C. D.
3.如图,△ABC中,∠C=90°,AD平分∠BAC,若AB=9,CD=2,则△ABD的面积是( )
A. B.9 C.18 D.
4.如图,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=15,BD=10,则点D到AB的距离是( )
A.15 B.10 C.8 D.5
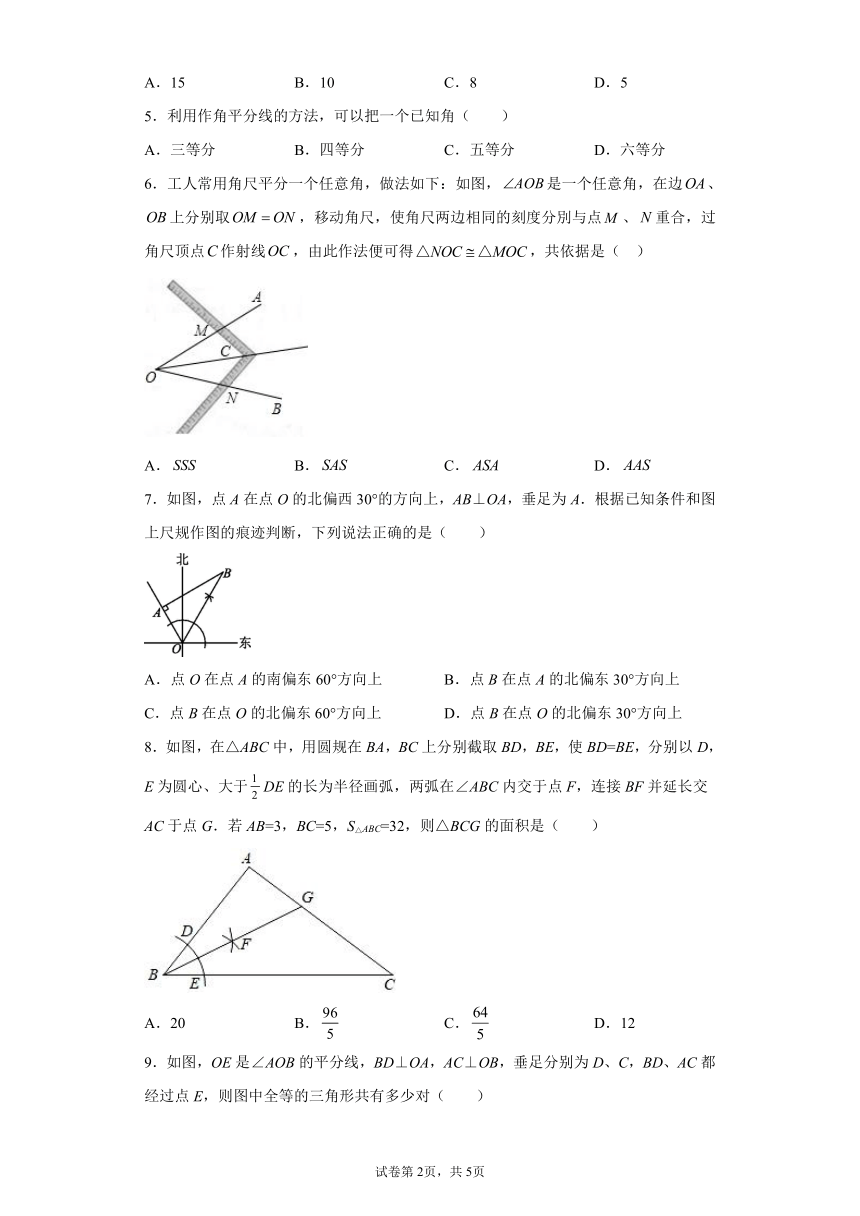
5.利用作角平分线的方法,可以把一个已知角( )
A.三等分 B.四等分 C.五等分 D.六等分
6.工人常用角尺平分一个任意角,做法如下:如图,是一个任意角,在边、上分别取,移动角尺,使角尺两边相同的刻度分別与点、重合,过角尺顶点作射线,由此作法便可得,共依据是( )
A. B. C. D.
7.如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是( )
A.点O在点A的南偏东60°方向上 B.点B在点A的北偏东30°方向上
C.点B在点O的北偏东60°方向上 D.点B在点O的北偏东30°方向上
8.如图,在△ABC中,用圆规在BA,BC上分别截取BD,BE,使BD=BE,分别以D,E为圆心、大于DE的长为半径画弧,两弧在∠ABC内交于点F,连接BF并延长交AC于点G.若AB=3,BC=5,S△ABC=32,则△BCG的面积是( )
A.20 B. C. D.12
9.如图,OE是∠AOB的平分线,BD⊥OA,AC⊥OB,垂足分别为D、C,BD、AC都经过点E,则图中全等的三角形共有多少对( )
A.3 B.4 C.5 D.6
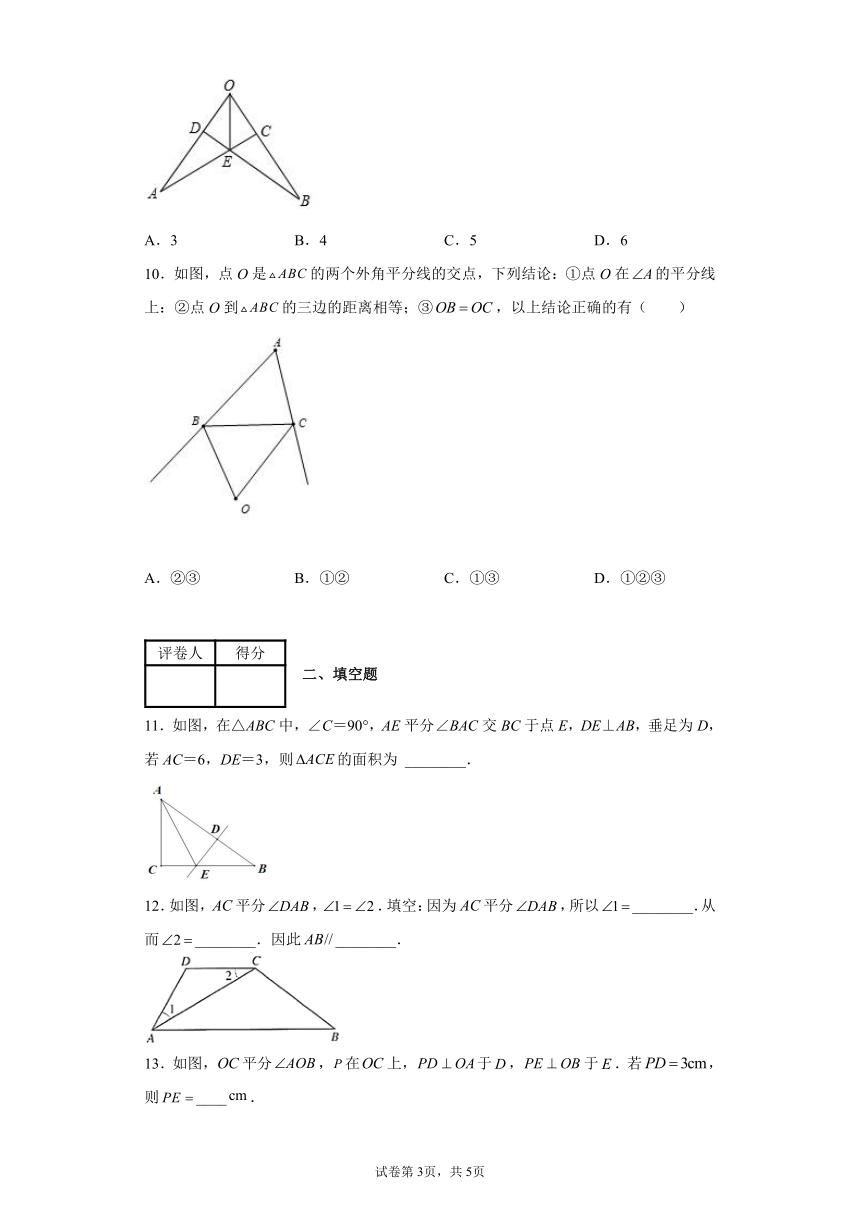
10.如图,点O是的两个外角平分线的交点,下列结论:①点O在的平分线上:②点O到的三边的距离相等;③,以上结论正确的有( )
A.②③ B.①② C.①③ D.①②③
评卷人得分
二、填空题
11.如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,DE⊥AB,垂足为D,若AC=6,DE=3,则的面积为 ________.
12.如图,平分,.填空:因为平分,所以________.从而________.因此________.
13.如图,平分,在上,于,于.若,则____.
14.如图,在 Rt△ABC 中,∠C=90 ,以顶点A 为圆心,适当长为半径画弧,分别交AC,AB 于点 M 、N,再分别以点M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点D,若CD=3,AB=10,则△ABD 的面积是________.
评卷人得分
三、解答题
15.求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
已知:如图,在中,角平分线与角平分线相交于点P,过点P分别作的垂线,垂足分别是D,E,F.
求证:的平分线经过点P,且.
16.如图,过点N作射线NM∥OA,并在直线NM上求作一点P,使点P到射线OA和OB的距离相等.(要求用尺规作图,保留作图痕迹,不必写作法和证明过程)
17.太和中学校园内有一块直角三角形(RtABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
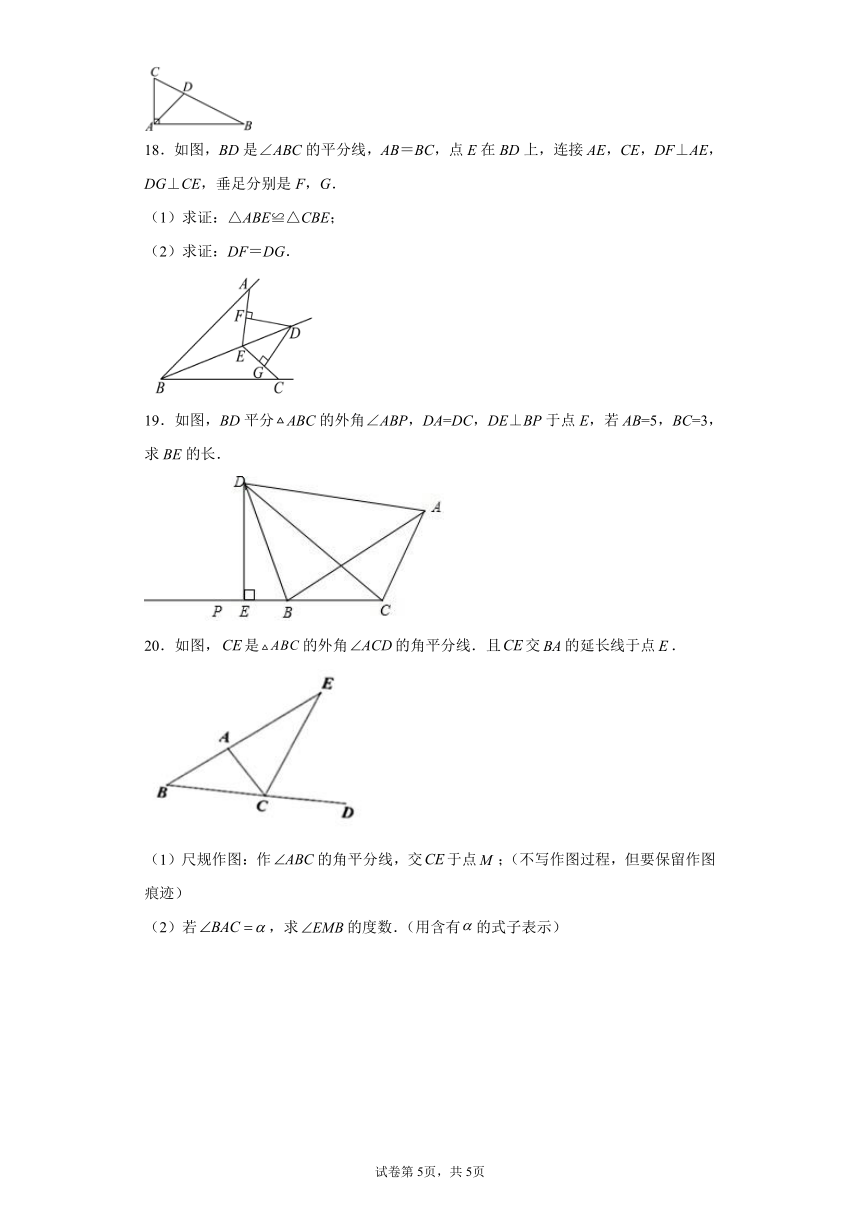
18.如图,BD是∠ABC的平分线,AB=BC,点E在BD上,连接AE,CE,DF⊥AE,DG⊥CE,垂足分别是F,G.
(1)求证:△ABE≌△CBE;
(2)求证:DF=DG.
19.如图,BD平分ABC的外角∠ABP,DA=DC,DE⊥BP于点E,若AB=5,BC=3,求BE的长.
20.如图,是的外角的角平分线.且交的延长线于点.
(1)尺规作图:作的角平分线,交于点;(不写作图过程,但要保留作图痕迹)
(2)若,求的度数.(用含有的式子表示)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
解:设这个点为点P,
∵点P到AB、AC两边的距离相等,
∴点P在∠BAC的平分线上,
同理可得点P在∠ABC、∠ACB的平分线上,
∴点P为三个内角的角平分线的交点,
故选:B.
2.A
解:∵AD是△ABC的角平分线,∠C=90°,DE⊥AB,CD=10,
∴DE=CD=10,
故选:A.
3.B
解:作DE⊥AB于E,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=DC=2,
∴△ABD的面积=×9×2=9,
故选:B.
4.D
解:过D点作DE⊥AB于E,如图,
∵BC=15,BD=10,
∴CD=BC-BD=5,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC=5,
∴点D到AB的距离为5.
故选:D.
5.B
【解】利用作角平分线的方法,可以把一个已知角二等分,进而可以将两角再次等分,故可以把一个已知角四等分.
故选:B.
6.A
解:由作图过程可得MO=NO,NC=MC,
在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
7.D
解:如图由题意:,
,
由作图可知,平分,
在点的北偏西的方向上
∴点在点北偏东方向上,
故选D
其它几个选项错误的原因如下:
由方位角可知.
所以点在点的南偏东方向上,故A项错误;
所以点在点北偏东方向上,故B项错误;
点在点北偏东方向上,故C项错误.
故选D
8.A
解:由作法得BG平分∠ABC,
作GM⊥AB于M,GN⊥BC于N,如图,
则GM=GN,
∵S△GAB+S△GBC=S△ABC,
∴GM×3+GN×5=32,
即3GN+5GN=64,解得GN=8,
∴S△GBC=×5×8=20.
故选:A.
9.B
解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,,,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
∴△OAC≌△OBD(SAS).
故选B.
10.B
【解】
过点分别作,如图,
点O是的两个外角平分线的交点,
,
,,
点O到的三边的距离相等;
故②正确;
,
点O在的平分线上,
故①正确;
连接,
假设,
,是的角平分线, ,
,,
,,
,,
,
即,
不一定等于,
故③不成立;
故正确的有①②.
故选B.
11.9解:∵AE平分∠BAC,DE⊥AB,∠C=90°,
∴,
∵,
∴.
故答案为:9.
12.
解:∵AC平分∠DAB,
∴∠1=∠CAB.
又∵∠1=∠2,
∴∠CAB=∠2,
∴ABDC(内错角相等,两直线平行).
故答案为:∠CAB,∠CAB,DC.
13.3解:∵OC平分∠AOB,点P在OC上,且PD⊥OA于D,PE⊥OB于E,PD=3cm,
∴PE=PD=3.
故答案为:3.
14.15【解】
如图,过点D作DH⊥AB于H.
∵AP平分∠CAB,DC⊥AC,DH⊥AB,
∴DC=DH=3,
∴S△ABD=AB×DH=×10×3=15,
故答案为:15.
15【解】
证明:∵是的角平分线,点P在上,,,
∴(角平分线上的点到这个角的两边的距离相等).
同理,.
∴.
∵,,
∴点P在的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),
即的平分线经过点P.
16.解:如图,点P为所作.
17.解:过点分别作,是垂足.
由,得,,
是的平分线,
.
18.【解】(1) BD是∠ABC的平分线,
,
在与中,
,
(2)
,
∴,
又∵,
∴.
19.解:过点D作BA的垂线交AB于点H,
∵BD平分△ABC的外角∠ABP,DH⊥AB,
∴DE=DH,
在Rt△DEB和Rt△DHB中,,
∴Rt△DEB≌Rt△DHB(HL),
∴BE=BH,
在Rt△DEC和Rt△DHA中,
,
∴Rt△DEC≌Rt△DHA(HL),
∴AH=CE,
由图易知:
AH=AB BH,CE=BE+BC,
∴AB BH=BE+BC,
∴BE+BH=AB BC=5 3=2,
而BE=BH,
∴2BE=2,
故BE=1.
20.【解】(1)作图如下:
;
(2)平分,
,
平分,
,
,
,
.
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.到△ABC的三边距离相等的点是△ABC的( )
A.三边中线的交点 B.三条角平分线的交点 C.三边上高的交点 D.三边垂直平分线的交点
2.如图,在Rt△ABC中,∠C=90°,AD是∠BAC平分线,DE⊥AB,垂足为E,若CD=10,则DE的长度为( )
A. B. C. D.
3.如图,△ABC中,∠C=90°,AD平分∠BAC,若AB=9,CD=2,则△ABD的面积是( )
A. B.9 C.18 D.
4.如图,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=15,BD=10,则点D到AB的距离是( )
A.15 B.10 C.8 D.5
5.利用作角平分线的方法,可以把一个已知角( )
A.三等分 B.四等分 C.五等分 D.六等分
6.工人常用角尺平分一个任意角,做法如下:如图,是一个任意角,在边、上分别取,移动角尺,使角尺两边相同的刻度分別与点、重合,过角尺顶点作射线,由此作法便可得,共依据是( )
A. B. C. D.
7.如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是( )
A.点O在点A的南偏东60°方向上 B.点B在点A的北偏东30°方向上
C.点B在点O的北偏东60°方向上 D.点B在点O的北偏东30°方向上
8.如图,在△ABC中,用圆规在BA,BC上分别截取BD,BE,使BD=BE,分别以D,E为圆心、大于DE的长为半径画弧,两弧在∠ABC内交于点F,连接BF并延长交AC于点G.若AB=3,BC=5,S△ABC=32,则△BCG的面积是( )
A.20 B. C. D.12
9.如图,OE是∠AOB的平分线,BD⊥OA,AC⊥OB,垂足分别为D、C,BD、AC都经过点E,则图中全等的三角形共有多少对( )
A.3 B.4 C.5 D.6
10.如图,点O是的两个外角平分线的交点,下列结论:①点O在的平分线上:②点O到的三边的距离相等;③,以上结论正确的有( )
A.②③ B.①② C.①③ D.①②③
评卷人得分
二、填空题
11.如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,DE⊥AB,垂足为D,若AC=6,DE=3,则的面积为 ________.
12.如图,平分,.填空:因为平分,所以________.从而________.因此________.
13.如图,平分,在上,于,于.若,则____.
14.如图,在 Rt△ABC 中,∠C=90 ,以顶点A 为圆心,适当长为半径画弧,分别交AC,AB 于点 M 、N,再分别以点M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点D,若CD=3,AB=10,则△ABD 的面积是________.
评卷人得分
三、解答题
15.求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
已知:如图,在中,角平分线与角平分线相交于点P,过点P分别作的垂线,垂足分别是D,E,F.
求证:的平分线经过点P,且.
16.如图,过点N作射线NM∥OA,并在直线NM上求作一点P,使点P到射线OA和OB的距离相等.(要求用尺规作图,保留作图痕迹,不必写作法和证明过程)
17.太和中学校园内有一块直角三角形(RtABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
18.如图,BD是∠ABC的平分线,AB=BC,点E在BD上,连接AE,CE,DF⊥AE,DG⊥CE,垂足分别是F,G.
(1)求证:△ABE≌△CBE;
(2)求证:DF=DG.
19.如图,BD平分ABC的外角∠ABP,DA=DC,DE⊥BP于点E,若AB=5,BC=3,求BE的长.
20.如图,是的外角的角平分线.且交的延长线于点.
(1)尺规作图:作的角平分线,交于点;(不写作图过程,但要保留作图痕迹)
(2)若,求的度数.(用含有的式子表示)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
解:设这个点为点P,
∵点P到AB、AC两边的距离相等,
∴点P在∠BAC的平分线上,
同理可得点P在∠ABC、∠ACB的平分线上,
∴点P为三个内角的角平分线的交点,
故选:B.
2.A
解:∵AD是△ABC的角平分线,∠C=90°,DE⊥AB,CD=10,
∴DE=CD=10,
故选:A.
3.B
解:作DE⊥AB于E,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=DC=2,
∴△ABD的面积=×9×2=9,
故选:B.
4.D
解:过D点作DE⊥AB于E,如图,
∵BC=15,BD=10,
∴CD=BC-BD=5,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC=5,
∴点D到AB的距离为5.
故选:D.
5.B
【解】利用作角平分线的方法,可以把一个已知角二等分,进而可以将两角再次等分,故可以把一个已知角四等分.
故选:B.
6.A
解:由作图过程可得MO=NO,NC=MC,
在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
7.D
解:如图由题意:,
,
由作图可知,平分,
在点的北偏西的方向上
∴点在点北偏东方向上,
故选D
其它几个选项错误的原因如下:
由方位角可知.
所以点在点的南偏东方向上,故A项错误;
所以点在点北偏东方向上,故B项错误;
点在点北偏东方向上,故C项错误.
故选D
8.A
解:由作法得BG平分∠ABC,
作GM⊥AB于M,GN⊥BC于N,如图,
则GM=GN,
∵S△GAB+S△GBC=S△ABC,
∴GM×3+GN×5=32,
即3GN+5GN=64,解得GN=8,
∴S△GBC=×5×8=20.
故选:A.
9.B
解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,,,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
∴△OAC≌△OBD(SAS).
故选B.
10.B
【解】
过点分别作,如图,
点O是的两个外角平分线的交点,
,
,,
点O到的三边的距离相等;
故②正确;
,
点O在的平分线上,
故①正确;
连接,
假设,
,是的角平分线, ,
,,
,,
,,
,
即,
不一定等于,
故③不成立;
故正确的有①②.
故选B.
11.9解:∵AE平分∠BAC,DE⊥AB,∠C=90°,
∴,
∵,
∴.
故答案为:9.
12.
解:∵AC平分∠DAB,
∴∠1=∠CAB.
又∵∠1=∠2,
∴∠CAB=∠2,
∴ABDC(内错角相等,两直线平行).
故答案为:∠CAB,∠CAB,DC.
13.3解:∵OC平分∠AOB,点P在OC上,且PD⊥OA于D,PE⊥OB于E,PD=3cm,
∴PE=PD=3.
故答案为:3.
14.15【解】
如图,过点D作DH⊥AB于H.
∵AP平分∠CAB,DC⊥AC,DH⊥AB,
∴DC=DH=3,
∴S△ABD=AB×DH=×10×3=15,
故答案为:15.
15【解】
证明:∵是的角平分线,点P在上,,,
∴(角平分线上的点到这个角的两边的距离相等).
同理,.
∴.
∵,,
∴点P在的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),
即的平分线经过点P.
16.解:如图,点P为所作.
17.解:过点分别作,是垂足.
由,得,,
是的平分线,
.
18.【解】(1) BD是∠ABC的平分线,
,
在与中,
,
(2)
,
∴,
又∵,
∴.
19.解:过点D作BA的垂线交AB于点H,
∵BD平分△ABC的外角∠ABP,DH⊥AB,
∴DE=DH,
在Rt△DEB和Rt△DHB中,,
∴Rt△DEB≌Rt△DHB(HL),
∴BE=BH,
在Rt△DEC和Rt△DHA中,
,
∴Rt△DEC≌Rt△DHA(HL),
∴AH=CE,
由图易知:
AH=AB BH,CE=BE+BC,
∴AB BH=BE+BC,
∴BE+BH=AB BC=5 3=2,
而BE=BH,
∴2BE=2,
故BE=1.
20.【解】(1)作图如下:
;
(2)平分,
,
平分,
,
,
,
.
